Version interactive avec LaTeX compilé
Abstract
AVERTISSEMENT Ce sujet comporte un problème de thermodynamique et un problème de chimie.
La composition doit impérativement être faite sur deux copies séparées et numérotées séparément. Chaque copie et chaque page intercalaire doit indiquer l'indication «Thermodynamique» ou «Chimie»
L'utilisation de la calculatrice est autorisée.
Chaque candidat doit disposer d'une feuille de papier millimétré.
Chaque candidat doit disposer d'une feuille de papier millimétré.
CHIMIE
A propos d'aluminium.
I - Quelques réactions de l'aluminium et de ses sels .
Les données se trouvent en fin de texte.
Chaque candidat dispose d'une feuille de papier millimétré.
Chaque candidat dispose d'une feuille de papier millimétré.
Expérience 1.
On prépare une solution
On ajoute ensuite progressivement une solution d'hydroxyde de sodium très concentrée (de façon à pouvoir négliger la variation de volume due à cette addition de soude) .
Il y a tout d'abord, alors que le pH est encore acide, apparition d'un précipité blanc laiteux ; on note
En poursuivant l'addition de la soude, on observe l'épaississement de ce précipité puis sa dissolution progressive ; le milieu est franchement basique lorsque le précipité disparaît : on note
On ajoute ensuite progressivement une solution d'hydroxyde de sodium très concentrée (de façon à pouvoir négliger la variation de volume due à cette addition de soude) .
Il y a tout d'abord, alors que le pH est encore acide, apparition d'un précipité blanc laiteux ; on note
En poursuivant l'addition de la soude, on observe l'épaississement de ce précipité puis sa dissolution progressive ; le milieu est franchement basique lorsque le précipité disparaît : on note
Expérience 2.
Dans un récipient, on introduit
Il y a dégagement d'un gaz incolore qui se poursuit jusqu'à la disparition totale de la poudre métallique.
On vérifie que le volume de la solution limpide obtenue à la fin du dégagement gazeux est encore
Il y a dégagement d'un gaz incolore qui se poursuit jusqu'à la disparition totale de la poudre métallique.
On vérifie que le volume de la solution limpide obtenue à la fin du dégagement gazeux est encore
Expérience 3.
On recommence l'expérience précédente en remplaçant la solution acide par de la soude de même concentration. On observe le dégagement du même gaz incolore jusqu'à disparition de la poudre d'aluminium. Le volume de la solution limpide
Expérience 4.
A la solution
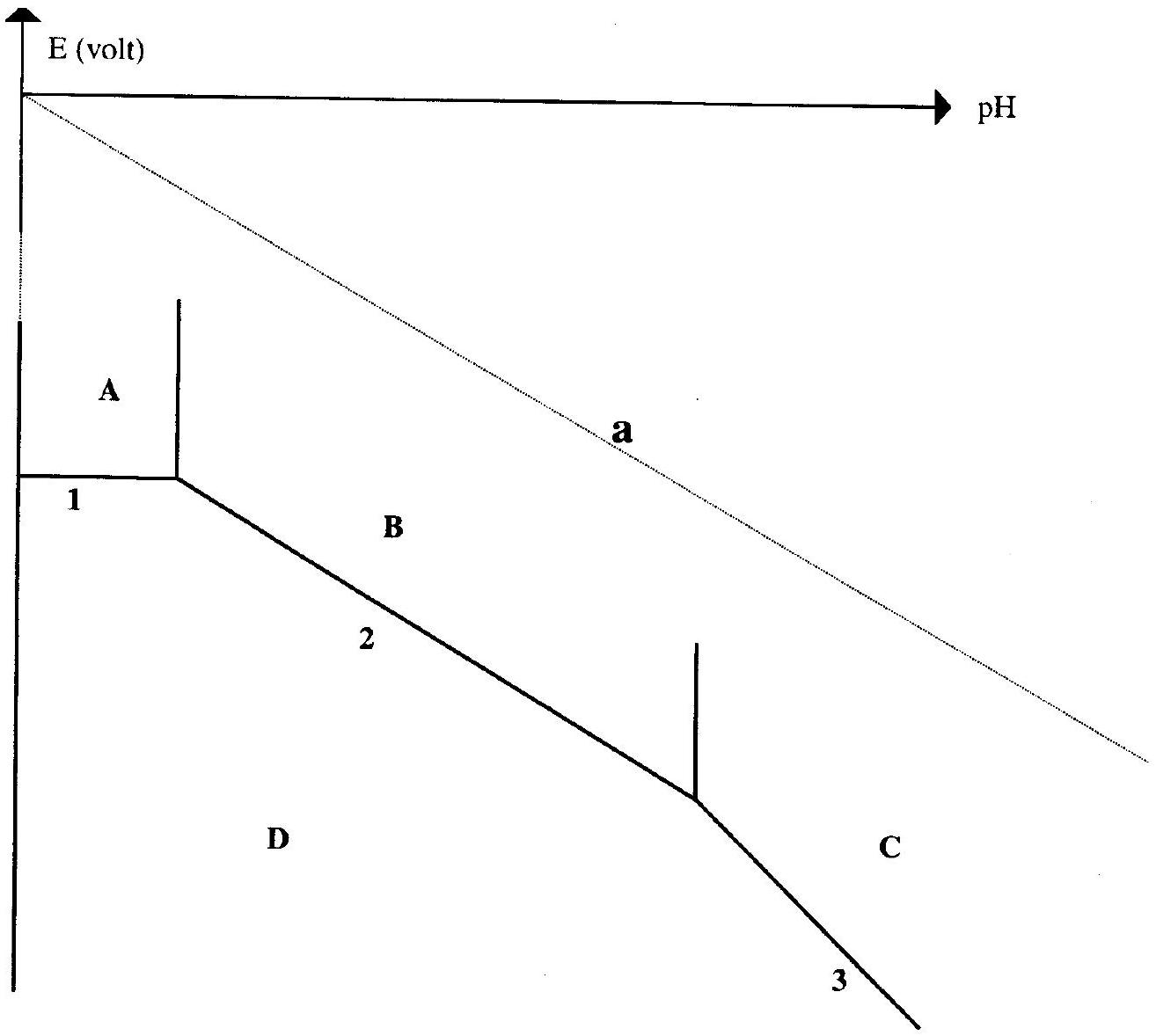
Pour interpréter ces expériences, on dispose de l'allure du diagramme
On donne les équations des tracés, les potentiels étant exprimés en V :
(1)
(2)
(3)
On donne les équations des tracés, les potentiels étant exprimés en V :
(1)
(2)
(3)
Le tracé (a) correspond au couple
- Indiquer la correspondance entre les lettres
et D et les espèces intervenant dans le tracé :
- espèces dissoutes :
et (ion aluminate) - espèces solides :
et (hydroxyde d'aluminium).
- Donner les demi équations électroniques des couples redox représentés sur ce diagramme .
- Donner les équation - bilans des réactions :
a) de précipitation puis de dissolution observées dans l'expérience 1 .
b) de la poudre d'aluminium avec l'acide chlorhydrique dans l'expérience 2.
c) de la poudre d'aluminium avec l'hydroxyde de sodium dans l'expérience 3. - Calculer les pH mentionnés dans les trois premières expériences .
- Qu'observe-t-on dans l'expérience 4 ?
Donner les équation - bilans des réactions successives .
II - Etude d'un alliage binaire d'aluminium et de magnésium .
Le magnésium cristallise dans un système hexagonal compact; le côté de l'hexagone est
- Dessiner les mailles de chacun des deux métaux .
- Comparer les rayons atomiques de l'aluminium et du magnésium .
- On désire construire le diagramme isobare de cristallisation du système binaire aluminium - magnésium sachant que les solides ne sont pas miscibles et que le liquide est homogène . Pour cela, on étudie les courbes de refroidissement de différents mélanges liquides aluminium- magnésium de fractions molaires en aluminium notées . t est la température mesurée en degré Celsius et est le temps .
On constate sur ces courbes d'analyse thermique des ruptures de pente et des paliers horizontaux .
On note :
On note :
-
la température de rupture de pente, quand elle existe -
la température du palier observé .
On obtient les résultats ci-dessous :
|
|
0,00 | 0,2 | 0,28 | 0,35 | 0,40 | 0,55 | 0,60 | 0,66 | 0,80 | 1,00 |
|
|
- | 500 | - | 455 | - | - | - | - | 545 | - |
|
|
650 | 440 | 440 | 440 | 460 | 455 | 470 | 465 | 465 | 660 |
- Reconstituer l'allure des courbes de refroidissement pour les fractions molaires
et . Préciser sur chacune des portions de courbe la variance du système binaire . - L'analyse thermique fait apparaître deux composés définis notés
et ; à quelles fractions molaires x correspondent-ils ? En déduire leurs formules . - a) Quelle est la particularité d'un mélange eutectique ?
b) Combien l'analyse thermique du système binaire aluminium - magnésium fait-elle apparaître de mélanges eutectiques ? - a) Tracer le diagramme binaire
pour une température comprise entre et .
Echelle imposée : abscisse:pour 0,1 unité ordonnée: 1 cm pour .
b) Indiquer la nature des phases en présence dans chacun des domaines du graphe précédent . - On prépare à haute température, un liquide homogène contenant 1,8 mole d'aluminium et 0,2 mole de magnésium. On le refroidit lentement .
a) Tracer l'allure de la courbe de refroidissementde ce système .
b) Calculer les quantités de matière dans chacune des phases àt.
En déduire les masses des différentes phases .
Données : masses atomiques en g.mol
couple (a)
Diagramme E - pH de l'aluminium .
Fin du problème de chimie
Thermodynamique.
Etude d'une installation exploitant l'énergie géothermique.
I) Evolution de la température dans la croûte terrestre.
La croûte terrestre est considérée comme homogène. De l'énergie y est libérée, avec une puissance volumique
Données du problème :
Conductivité thermique du sous - sol:
Capacité thermique volumique du sous-sol :
Puissance volumique libérée au sein de la croûte terrestre:
Flux thermique surfacique à la surface (en
Température du sol à la surface (en
Conductivité thermique du sous - sol:
Capacité thermique volumique du sous-sol :
Puissance volumique libérée au sein de la croûte terrestre:
Flux thermique surfacique à la surface (en
Température du sol à la surface (en
- Etablir, en régime permanent, l'équation différentielle vérifiée par
. - En déduire
. - A quelle profondeur faut-il forer pour rencontrer une température égale à
? - Calculer la puissance thermique produite dans un volume de roche égal à
. Proposer une origine pour ce phénomène . - Calculer la puissance thermique à travers une surface de
découpée sur le plan .
II) Etude d'un module expérimental.
L'exploitation envisagée consiste à forer au moins deux puits voisins. L'un des puits sert à extraire une saumure (liquide) chaude, l'autre à la réinjecter, plus froide, dans le sous-sol après qu'elle ait fourni de l'énergie dans l'usine d'exploitation. Les deux puits sont en communication souterraine par un réseau de fractures naturelles ou artificielles. La saumure froide réinjectée pourra donc se réchauffer à nouveau au contact des roches profondes. On considère un module expérimental où la saumure est extraite à la température
- Calculer la puissance thermique extraite, littéralement et numériquement.
- Etablir l'expression du rendement r d'une machine motrice ditherme réversible (cycle de Carnot).
- La saumure chaude sert de source chaude, dont la température varie de
à , pour un moteur thermique dont la source froide est à la température constante .
Calculer littéralement et numériquement la puissance mécanique maximale récupérable avec cette installation et le rendement global
4) des considérations cinétiques conduisent à admettre une expression plus réaliste du rendement d'une machine motrice ditherme:
III) Les deux puits ont une profondeur égale à 5000 m . Ils sont complètement remplis de saumure.
4) des considérations cinétiques conduisent à admettre une expression plus réaliste du rendement d'une machine motrice ditherme:
III) Les deux puits ont une profondeur égale à 5000 m . Ils sont complètement remplis de saumure.
1 ) En négligeant les variations de la pesanteur avec
2) La saumure chaude prélevée à la profondeur de 5000 m reste à température constante durant toute la remontée dans le puits d'extraction. On rappelle la relation empirique de Duperray concernant la pression de vapeur saturante de l'eau :
3) Montrer qu'une pression du fluide supérieure à 15 bars en tête de puits, c'est àdire pour
IV) Echangeur à contre-courant.
2) La saumure chaude prélevée à la profondeur de 5000 m reste à température constante durant toute la remontée dans le puits d'extraction. On rappelle la relation empirique de Duperray concernant la pression de vapeur saturante de l'eau :
3) Montrer qu'une pression du fluide supérieure à 15 bars en tête de puits, c'est àdire pour
IV) Echangeur à contre-courant.
L'échangeur , supposé parfaitement calorifugé, est siège d'un transfert thermique entre deux liquides circulant à contre-courant :
- la saumure, de débit massique
, de capacité thermique massique dont la température est à l'entrée et à la sortie de l'échangeur. - un fluide f , de débit massique
, de capacité thermique massique à pression constante , qui entre dans l'échangeur à la température et en ressort à la température ( voir les figures 1 et 2 ).
L'échangeur est modélisé par deux conduites de sections rectangulaires, séparées par une plaque métallique de longueur, de largeur a et d'épaisseur e . La conductivité thermique du métal constituant la plaque est . L'ensemble est parfaitement calorifugé.
Sur les figures 1 et 2 , la plaque métallique est hachurée.
L'échangeur est repéré par un axe Ox, parallèle aux écoulements et un axe Oz perpendiculaire à Ox : voir la figure 2. Le plan xOy est plan de symétrie de la plaque.
On se propose de déterminer, en régime stationnaire, les températures respectiveset des fluides traversant l'échangeur. Les variations d'énergie cinétique et d'énergie potentielle de pesanteur des fluides sont négligées.
1 ) On considère une tranche d'échangeur comprise entre les abscisses x et
2 ) Ecrire le bilan thermique de la saumure entre les abscisses
3 ) Ecrire le bilan thermique du fluide f entre les abscisses x et
4) En déduire une relation simple entre
3 ) Ecrire le bilan thermique du fluide f entre les abscisses x et
4) En déduire une relation simple entre
5 ) En déduire l'équation différentielle vérifiée par
6 ) Intégrer cette équation différentielle dans le cas où
7 ) Calculer alors la valeur de a si
8 ) Si la valeur de a vous paraît excessive, comment procéder pour rendre l'échangeur moins encombrant
6 ) Intégrer cette équation différentielle dans le cas où
7 ) Calculer alors la valeur de a si
8 ) Si la valeur de a vous paraît excessive, comment procéder pour rendre l'échangeur moins encombrant
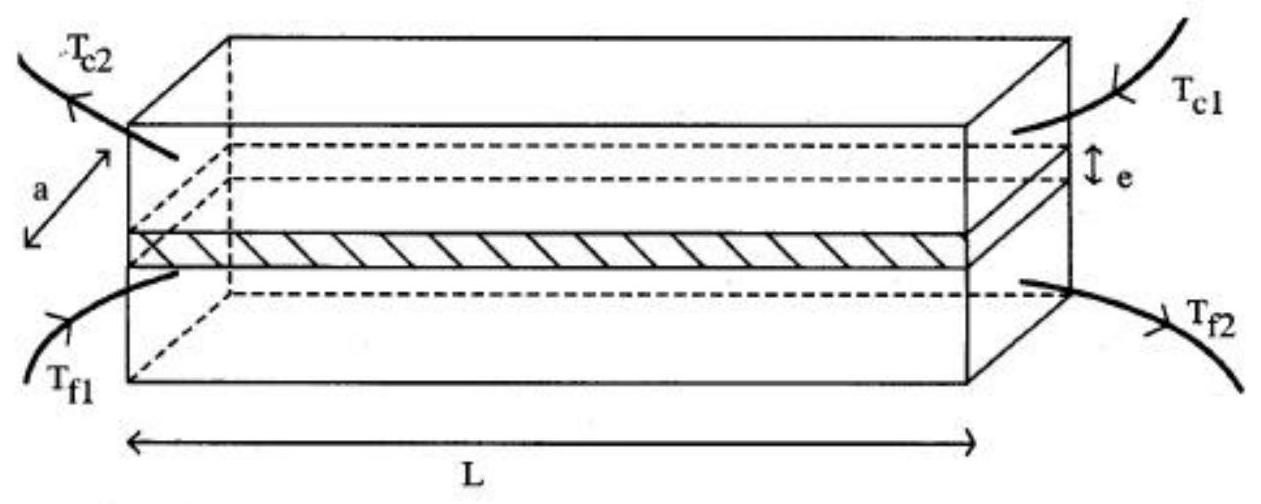
Figure 1
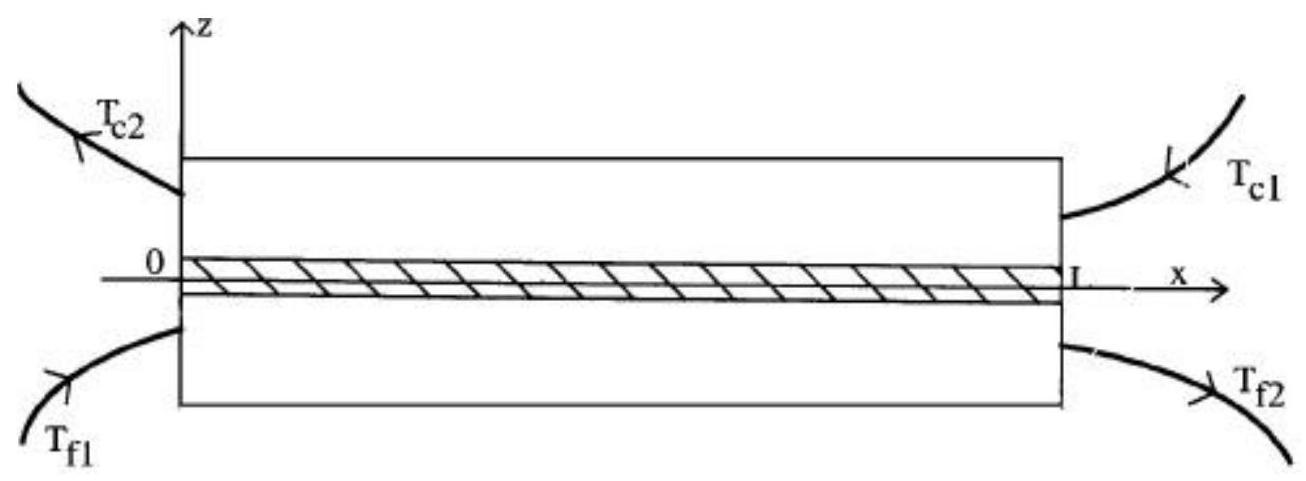
Figure 2
Fin du problème de thermodynamique
