J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Banque PT Physique A PT 2005

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo banque-pt
🔗 Explorer
Banque
Banque PT
Année
2005
Filière
PT
Matière
Physique
Banque PT PTBanque PT 2005PT PhysiquePhysique 2005
2025_09_04_4c3da601044b6d200114g

Epreuve de Physique A

Durée 4 h

AVERTISSEMENT

L'utilisation de la calculatrice est autorisée.
Au début de chaque partie, son «poids» dans le barème est indiqué en pourcentage.
Si , au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

SISMOMETRIE

Le but de ce problème est de présenter le principe de fonctionnement des sismomètres qui sont utilisés pour mesurer et enregistrer les déplacements du sol causés par les tremblements de terre. A partir des enregistrements réalisés (voir un exemple Figure 1), l'appareil est alors plutôt appelé un sismographe, il est possible de déterminer la localisation ou épicentre des séismes ainsi que leur "magnitude" ; à partir de ces informations les géophysiciens peuvent conduire des études géologiques à grande échelle comme l'étude du mécanisme même des séismes ou la caractérisation de la structure la croûte terrestre. A côté de l'étude des séismes "naturels" il existe aussi des micro-tremblements de terre artificiels provoqués par des explosions et enregistrés eux aussi, par des sismographes ; cela permet une étude géologique plus locale voire de la prospection minière ou pétrolière.
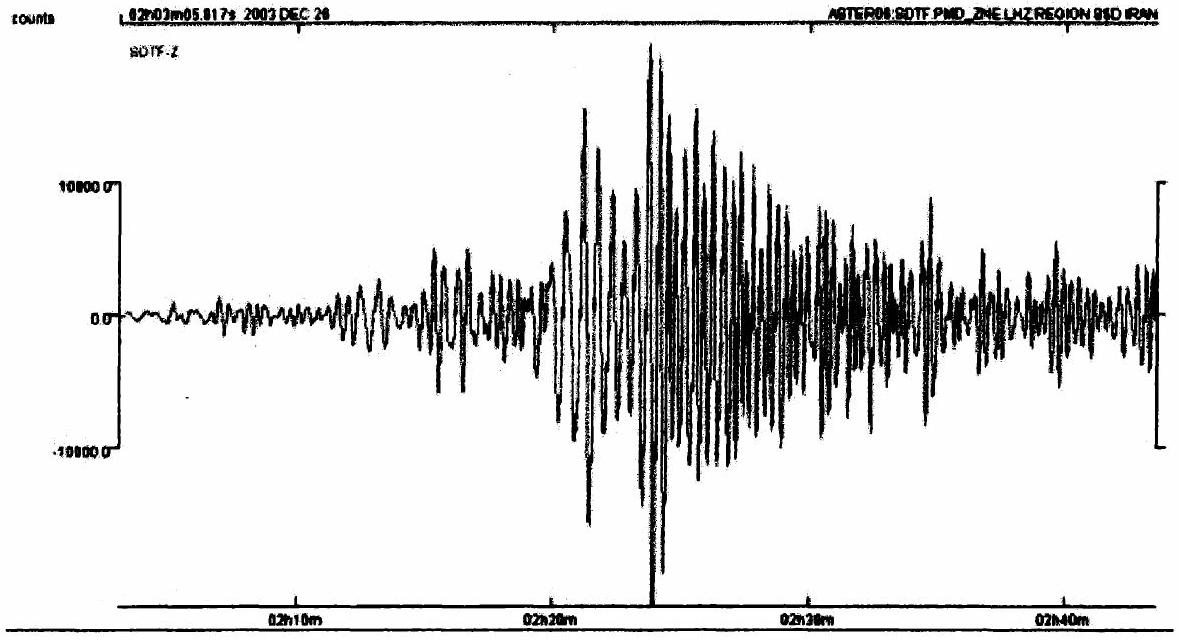
Figure 1. Enregistrement effectué dans les Alpes-Maritimes du séisme du 26 décembre 2003 en Iran.

è Partie - Principe de fonctionnement d'un sismomètre

(40 % du barème de ce problème)

I. Principe de la dynamique

  1. Donner l'expression du principe fondamental de la dynamique pour un point matériel dans un référentiel galiléen, noté .
  2. Même question dans le cas d'un référentiel non galiléen, noté .
  3. Application: déterminer l'angle d'inclinaison, supposé constant, d'un pendule simple de masse et de longueur , placé dans un véhicule, en translation rectiligne horizontale dans
    galiléen, et dont l'accélération supposée constante est notée ; on note l'intensité de la pesanteur.

II. Comportement élastique

Soit un ressort de longueur au repos et de constante de raideur .
  1. Donner l'expression de la force de rappel exercée par le ressort lorsqu'un opérateur lui donne, par traction, une longueur totale .
  2. On suppose maintenant que le ressort soit tel que, par un procédé particulier de fabrication, il faille exercer une force pour décoller les spires de ce ressort.
    2.1 Calculer la force de rappel exercée par le ressort lorsque l'opérateur lui a donné une longueur totale .
    2.2 A quelle condition sur obtient-on une force de rappel proportionnelle à la longueur totale du ressort?
    2.3 Que peut-on dire alors de la longueur apparente au repos de ce ressort ?
  3. La condition précédente étant difficile à réaliser on préfère réaliser un ressort pour lequel la force à exercer pour décoller les spires est et auquel on rajoute un brin de fil de longueur comme indiqué sur la Figure 2.
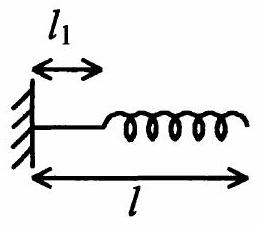
Figure 2.
3.1 Calculer la longueur à ajouter pour que le ressort exerce une force de rappel proportionnelle à la longueur totale .
3.2 Conclure sur le rôle du brin de fil de longueur .
DANS LA SUITE DU PROBLEME on considère que la Terre constitue un référentiel galiléen noté et que est uniforme. Localement le sol est mis en mouvement par rapport à sous l'effet des secousses sismiques que l'on souhaite étudier, secousses naturelles, en cas de tremblement de Terre, ou artificielles. On notera le référentiel lié au sol, au lieu d'observation. On s'intéresse uniquement dans ce problème au cas où est animé par rapport à d'un mouvement de translation verticale, mais bien sûr l'étude pourrait se généraliser à des mouvements de translation à trois dimensions.
4. Que peut-on dire, dans ce cas, du terme d'accélération de Coriolis (accélération complémentaire) ?

III. Principe de fonctionnement d'un sismomètre pendule

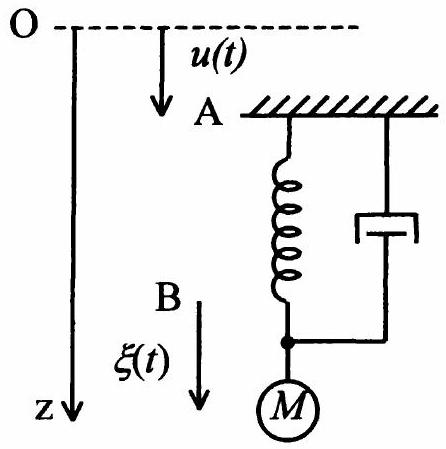
Le sismomètre pendule est constitué d'une masse reliée à un point A d'un chassis lui-même solidaire du sol en vibration dans . La liaison de au bâti est modélisée par un comportement élastique de constante de raideur associé à un frottement fluide caractérisé par la constante selon le schéma de la Figure 3. Le point B est également lié au chassis.
Figure 3. Modèle du sismomètre pendule
  1. Qu'appelle-t-on frottement fluide ou visqueux?
  2. On note Oz un axe vertical descendant, O étant fixe dans . Le mouvement du sol par rapport au référentiel galiléen est noté et le mouvement de par rapport au chassis, donc par rapport au sol, est noté . On suppose que est nul à l'équilibre en l'absence de tremblement de terre (donc lorsque est constamment nul).
    2.1 On pose: et .
En raisonnant dans le référentiel non-galiléen , montrer que l'équation différentielle du mouvement s'écrit : .
2.2 Dans le cas de mouvements très rapides (donc de très grandes fréquences), quel est le terme prépondérant (au premier membre)?
Quelle grandeur représente alors ?
2.3 Mêmes questions dans le cas de mouvements très lents.
3. Déterminer l'expression complexe de la réponse , en régime permanent sinusoïdal - ou harmonique forcé -, du système à un déplacement du sol de type sinusoïdal d'amplitude . On caractérise le mouvement enregistré par son amplitude et son déphasage et on introduit le paramètre .
3.1 Déterminer les expressions de et en fonction de et du rapport .
3.2 Étudier les comportements limites de et aux très basses, puis aux très hautes pulsations.
3.3 On pose . En exprimant en fonction de , montrer qu'il ne peut pas y avoir résonance si est supérieur à une valeur limite que l'on déterminera.
3.4 Tracer les courbes et pour les deux valeurs suivantes du paramètre : puis , les valeurs de et de étant fixées.
Que deviennent ces courbes pour nul?
4. On définit la sensibilité d'un pendule sismique par la valeur absolue du quotient du déplacement de la masse par la variation de l'accélération sismique qui provoque ce déplacement.
4.1 Exprimer en fonction de la période propre du pendule dans le cas de mouvements dits de longue période (donc de mouvements très lents).
4.2 Application numérique: calculer le déplacement de la masse , provoqué sur un pendule de période propre 60 s par une variation d'accélération du bâti de 1 milligal .
5. On considère que le sol est soumis à une accélération dont le graphe est donné Figure 4 ci-dessous.
Indiquer, qualitativement et sans calcul, le type de réponse dans le cas limite où , sachant que .
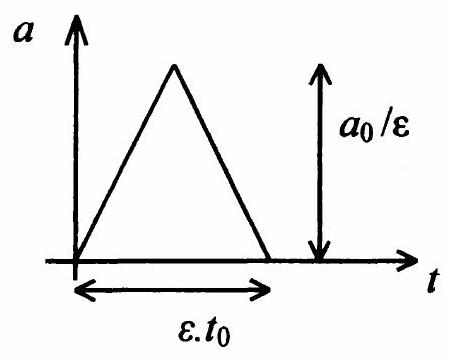
Figure 4. Accélération du sol.
Figure 5. Exemple de sismomètre "vertical", de type Galitzin (Jena, 1935).

IV - Exemple de sismomètre à longue période

Le sismomètre représenté ci-dessous Figure 6 est aussi appelé "sismomètre de LACOSTE". Il est constitué d'une masse située à l'extrémité d'une tige de masse négligée. La tige est mobile autour d'un axe horizontal Bx orthogonal au plan de la figure (liaison pivot idéale) ; on note la distance à l'axe Bx du centre d'inertie G de la masse M . Un ressort de constante de raideur est tendu entre un point A du bâti situé au-dessus de B , sur la même verticale (on note : ) et un point C de la tige, tel que .
Les mouvements du point G ont lieu dans le plan vertical.
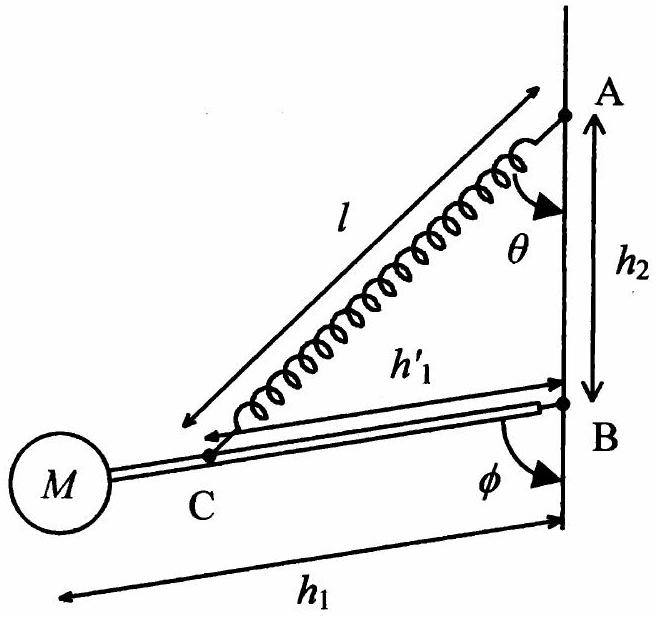
Figure 6. Sismomètre de LACOSTE.

1. Etude de l'équilibre du système en l'absence de mouvement du sol.

1.1 Etablir géométriquement une relation entre et .
1.2 Montrer que, pour un ressort dont la longueur au repos apparente (définie au II 2.3) est nulle, la condition d'équilibre -si elle existe- est indépendante de l'angle .
1.3 Quelle est la condition liant la masse et les longueurs fixées par le constructeur pour que cette position d'équilibre existe?
2. Un tel pendule possède en théorie une période infinie. Dans la pratique, la plus grande période que l'on ait pu obtenir pour ce type de pendule est de 80 s alors que les valeurs usuelles des sismomètres à longue période sont plutôt de 15 à 30 s . Quels facteurs peuvent intervenir limitant ainsi la période du pendule ?
Au vu des résultats de la question III. 4 de la première partie, rappeler le rôle de la période propre dans la sensibilité du pendule sismique en basse fréquence.

è Partie - Etude du sismomètre vertical GeOTECH SL210

(60 % du barème de ce problème)
Figure 7. Sismomètres Geotech SL-210 (mouvement vertical) au centre et SL-220 (mouvement horizontal) à gauche et à droite.

I. Etude du mouvement

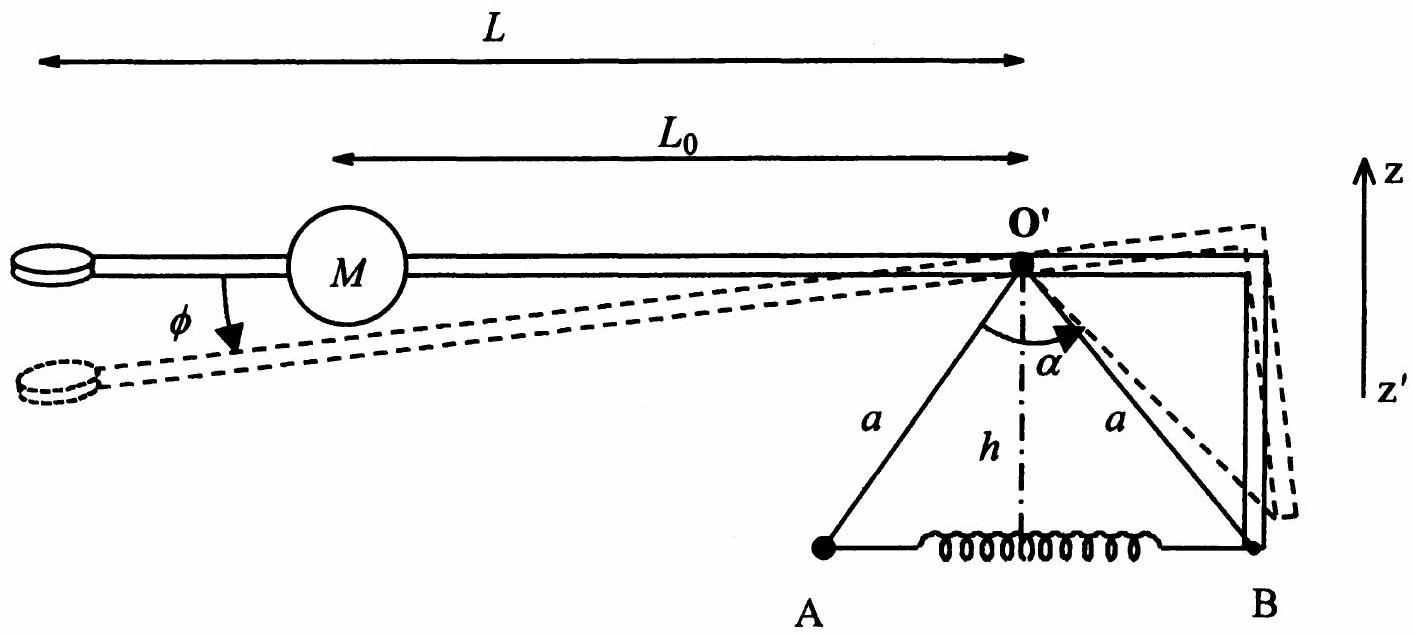
Figure 8. Sismomètre vertical GEOTECH.
Le sismomètre de la société Geotech, représenté ci-dessus Figure 8, comporte les éléments suivants :
  • un solide en forme de bras coudé à , pouvant tourner (liaison pivot idéale) autour d'un axe orienté O'x orthogonal au plan de figure, «sortant» (ou «piquant»), et lié au châssis, fixe dans (on précise que l'axe O'y serait orienté vers la droite, s'il était indiqué figure 8).
  • un ressort tendu entre A et B ;
  • une masse située sur la partie la plus longue du bras coudé, et dont le centre d'inertie G est à la distance de l'axe;
  • une bobine de mesure, solidaire du bras coudé, et située à la distance de .
Les points et A sont solidaires du châssis ; en revanche, le point B est lié au bras coudé (c'est l'extrémité de sa partie la plus courte).
On suppose, afin d'alléger les calculs, que les distances O'A et O'B sont égales et on pose : .
La bobine, de masse négligeable, est mobile dans l'entrefer d'un aimant et permet d'enregistrer les mouvements du sismomètre ; l'effet des éventuelles forces de Laplace est, dans toute cette partie I, négligé.
Le chassis suivant les mouvements du sol, le point se déplace ici encore selon la verticale en suivant le mouvement de translation rectiligne vertical du référentiel lié au sol par rapport au référentiel galiléen , mouvement donné par une loi .
Le bras coudé peut tourner d'un angle autour de l'axe O'x orthogonal au plan de figure. Lorsque l'angle est nul, la partie la plus longue du bras coudé est en position horizontale.
On suppose que l'on peut modéliser les frottements de contact du bras sur l'axe de rotation par un frottement de type visqueux.
Nota Bene : attention, l'axe z'Oz est ici vertical ascendant (voir la Figure 8, ci-dessus).
On utilisera - et on admettra - le fait que, dans , le torseur des forces d'inertie d'entraînement est, pour le système (bras coudé, masse M , bobine) et dans le cadre de cette étude, le même que si toute la masse du système étudié était concentrée au centre d'inertie de la masse M .
  1. En utilisant cette propriété et appliquant un théorème du moment cinétique dans le référentiel non galiléen , montrer que l'équation différentielle du mouvement du bras peut se mettre sous la forme :
où la forme analytique de la fonction ne sera étudiée qu'à la question 2 .
Préciser la signification physique de et .
2. Détermination de .
A toute valeur de la rotation du bras correspond une longueur du ressort dont la tension (ou force de rappel) a pour norme , la longueur étant ici supérieure à ( étant positive ou nulle). On appelle la distance de à l'axe du ressort. On note et les valeurs de , het correspondant au cas où l'angle est nul .
2.1 En l'absence de tremblement de terre (cas où ), l'angle est nul à l'équilibre du système dans le référentiel galiléen ; en déduire la relation entre et .
2.2 Sachant que le segment O'B est lié au bras coudé, donner la relation entre et .
2.3 Etablir géométriquement l'expression de en fonction de et de ; tester sa pertinence dans le cas particulier où vaudrait , soit .
2.4 Déterminer, de même, en fonction de et de .
2.5 En déduire l'expression de en fonction de et des constantes et g.
2.6 Pour de petites variations de autour de la position d'équilibre , effectuer le développement limité de au deuxième ordre (inclus).
2.7 Justifier que, pour qu'il n'y ait pas de dissymétrie dans le mouvement autour de la position d'équilibre, doit être une fonction impaire de .
Montrer que pour cela on doit avoir . Conclusion?
Cette condition est supposée réalisée dans les questions 2.8 à 3.2
2.8 Tenant compte du résultat précédent, vérifier que :
  1. Réglage du sismomètre à l'équilibre.
    3.1 En posant étudier le comportement du bras pour des valeurs petites de .
    3.2 On nomme la période propre des oscillations du châssis (en l'absence de frottement). Quel est l'intérêt de choisir l'angle petit?
    3.3 On ne conserve maintenant dans l'expression de que les termes d'ordre 1 en ; quel serait l'effet d'une longueur apparente au repos positive sur la période propre des oscillations? Conclusion?

II. Enregistrement électrique du mouvement d'un sismomètre

Une bobine de spires, de masse et d'auto-inductance négligeables et de résistance , liée au bras du sismomètre, est placée à la distance de O . Sa longueur et le diamètre de sa section droite sont supposés très faibles devant . Cette bobine est mobile dans le champ magnétique d'un aimant de forme torique, l'ensemble est représenté à la Figure 9. Le champ magnétique est supposé radial et de norme uniforme (notée B ) dans l'entrefer. L'aimant étant lié au châssis, donc au référentiel , le champ magnétique est permanent, dans ce même référentiel. Soit la longueur de fil de la bobine.
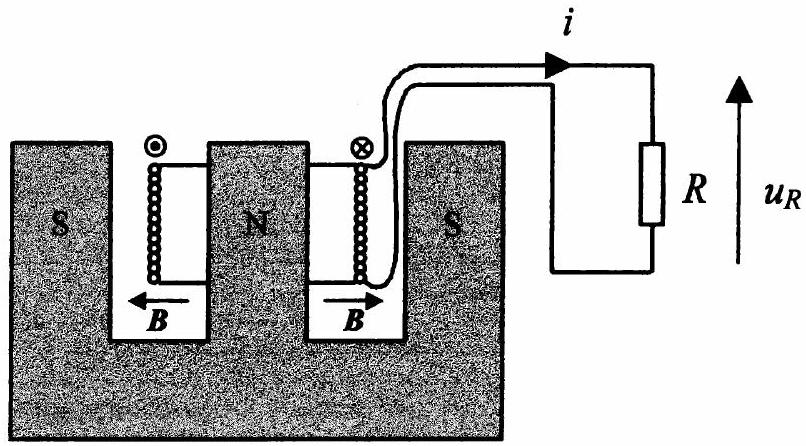
Dans la suite, l'angle est supposé très petit; les calculs seront limités à l'ordre 1 (inclus) en .
Figure 9. Montage avec une bobine permettant l'enregistrement du mouvement.

1. Équation différentielle du déplacement de la bobine.

1.1 La bobine est fermée sur une résistance . Montrer que l'intensité du courant qui circule dans le circuit est liée aux variations de l'angle par :
où est une grandeur que l'on déterminera en fonction de B et de la longueur du fil de la bobine.
On admet que, du fait des actions de Laplace, il apparaît un couple supplémentaire, de moment (par rapport à l'axe O'x orthogonal au plan de figure, et "sortant") égal à GLi .
1.2 En déduire l'équation différentielle du mouvement du bras, reliant l'angle et .
1.3 Donner le lien entre le déplacement de la bobine (compté positivement dans le sens ascendant) et l'angle . On suppose que s'annule en même temps que .
Sachant que (la notation a été définie au I. 1 de cette deuxième partie), montrer que l'équation différentielle du déplacement de la bobine, reliant le déplacement et , peut se mettre sous la forme :
où représente une grandeur appelée longueur réduite.
Donner l'expression de la pulsation propre et mettre le coefficient d'amortissement sous la forme et représentant respectivement l'amortissement mécanique et l'amortissement électrique.

2. Équation en tension du pendule.

Le sismomètre est utilisé avec un amplificateur qui amplifie la tension aux bornes de , et dont la résistance d'entrée est . La tension de sortie de l'amplificateur est notée ; on note son gain en tension : .
2.1 Comment sont modifiées les équations précédentes?
2.2 Etablir l'équation différentielle ( ) dite équation en tension du pendule.
On posera
2.3 Pour un déplacement sinusoïdal du sol , la tension est, en régime établi, sinusoïdale.
Calculer le rapport des amplitudes de la tension au déplacement, noté , ainsi que le déphasage de par rapport à .
2.4 On note la résistance totale du circuit et on introduit la grandeur dite résistance critique d'amortissement.
Exprimer en fonction de et .

3. Etalonnage du sismomètre.

3.1 étant connue, montrer que les mesures de la période propre et de permettent de calculer et .
3.2 Les valeurs de , et sont données par le constructeur du sismomètre :
Donner alors l'expression numérique de (en T.m) en fonction de , de (en ) et de (en s).
3.3 Détermination de et :
On étudie le mouvement, supposé pseudo-périodique du bras du sismomètre en circuit ouvert, et en l'absence de tremblement de terre.
Déterminer l'équation du mouvement et déterminer l'expression de en fonction de la pseudo-période ' et de .
3.4 On mesure alors le rapport de deux amplitudes successives et la pseudopériode . Calculer en fonction du décrément logarithmique , égal à .

3.5 Détermination de :

On étudie le mouvement, supposé pseudo-périodique, du bras du sismomètre lorsque la bobine est fermée sur une résistance équivalente choisie convenablement, et connue. Comment peut-on déterminer ?
Banque PT Physique A PT 2005 - Version Web LaTeX | WikiPrépa | WikiPrépa