N.B. : le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

RAPPEL DES CONSIGNES

Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
Ne pas utiliser de correcteur.
Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont interdites.

Le sujet est composé de cinq parties, pouvant être traitées indépendamment.
Important : vous pouvez utiliser les fonctions des questions précédentes, même si vous ne les avez pas toutes implémentées.

Vous devez répondre directement sur le Document Réponse, soit à l'emplacement prévu pour la réponse lorsque celle-ci implique une rédaction, soit en complétant les différents programmes en langage Python.

Le sujet comporte :

le texte du sujet : 10 pages;
les Annexes : 3 pages;
le Document Réponse (DR) : 8 pages.

Seul le Document Réponse est à rendre dans son intégralité.

Gestion de Tests dans une entreprise

Une entreprise d'e-commerce vend des meubles tous identifiés par une référence et par un QR code

. Tous les clients sont identifiés par leur numéro de sécurité sociale. Tous les achats s'effectuent à l'aide d'un numéro de carte de crédit. Cette entreprise met en œuvre différents tests afin d'éviter les erreurs de numéros de sécurité sociale, de numéros de carte de crédit ou de QR codes.

Partie I-Tests de code de sécurité sociale

En France, le numéro de sécurité sociale correspond au numéro d'inscription au répertoire national d'identification des personnes physiques (RNIPP). Il est formé du numéro d'inscription (NIR) à 13 chiffres et d'une clé de contrôle à 2 chiffres. Le NIR, créé à partir de l'état civil, est composé de la façon suivante :

Sexe (1 chiffre);
Année de naissance (les deux chiffres suivants);
Mois de naissance (les deux chiffres suivants);
Lieu de naissance (les cinq chiffres ou caractères suivants - 2 chiffres du code du département de naissance, suivis de 3 chiffres du code commune officiel de l'Insee );
Numéro d'ordre permettant de distinguer les personnes nées au même lieu à la même période (les 3 chiffres suivants).
Les deux derniers chiffres, compris entre 01 et 97 , permettent de déterminer la clé, appelée aussi "clé de contrôle", qui permettra de contrôler l'exactitude du numéro de sécurité sociale.

Pour obtenir cette clé, on détermine tout d'abord, le reste de la division par 97 du nombre formé par les 13 premiers chiffres. La clé correspond au résultat de ce nombre retranché de 97.

Exemple : soit le numéro de sécurité sociale à 13 chiffres : "2 910175018 002". Le reste de la division de 2910175018002 par 97 est égal à 29. La clé est constituée du résultat : 97-29 = 68. Le numéro de sécurité sociale complet est donc : "2910175018002 68".

Dans cette partie, le numéro de sécurité sociale de 13 chiffres est une chaîne de caractères composée uniquement de chiffres avec des espaces de séparation entre les différents éléments constituant ce numéro. On ne prendra pas en compte le cas de la Corse.

Ne pas oublier qu'il est toujours possible de transformer un nombre entier en une chaîne de caractères composées de chiffres (fonction str) et réciproquement (fonction int), (annexe 3).

Q1. Écrire la fonction num_secu qui, à partir de la chaîne de caractères d'un numéro de sécurité sociale, donne le numéro sous la forme d'un entier. Le programme devra parcourir la chaîne de caractères représentant le numéro de sécurité sociale en supprimant les caractères d'espacement, puis la transformer en un nombre entier. Cette fonction a un paramètre de type string et retourne une valeur de type int.

Un QR code (Quick Response code) désigne un type de code-barres en deux dimensions, lequel se compose de modules noirs disposés dans un carré à fond blanc (voir figure 1).
Pour simplifier le problème, nous supposons que les deux départements corses 2 A et 2 B sont représentés par le code 20 comme avant 1976.
Institut national de la statistique et des études économiques.

Exemple:

>>> num_secu("2 91 01 75 018 002")
2910175018002

Q2. Écrire la fonction clef qui détermine la valeur de la clé d'un numéro de sécurité sociale. Cette fonction a un paramètre de type int et retourne un élément de type int.

Exemple :

>>>clef(2910175018002)

68
Q3. Écrire la fonction num_secu_complet qui détermine le numéro complet de sécurité sociale. Cette fonction a un paramètre de type int et retourne un élément de type int.
Exemple :

>>>num_secu_complet(2910175018002)
291017501800268

Q4. Écrire la fonction test_num_secu qui détermine si un numéro de sécurité sociale est correct. Cette fonction a un paramètre de type string et retourne un élément de type bool.

Exemples:

>>>test_num_secu('2 91 01 75 018 002 68')
True
>>>test_num_secu('2 91 01 75 018 002 93')
False

Partie II - Test de numéro de carte de crédit

Pour savoir si un numéro de carte de crédit est valide, on utilise très souvent l'algorithme de Luhn

. Comme pour le numéro de sécurité sociale, il y a une clé appelée somme de contrôle (checksum en anglais) qui fait partie du numéro d'une carte de crédit. Ce numéro est un entier composé de 16 chiffres. Le dernier chiffre est la clé qui permet de contrôler l'exactitude du numéro.

Le principe de l'algorithme de Luhn est le suivant. On commence toujours par le chiffre se trouvant le plus à droite. Ce chiffre sera le premier élément de la liste dites des "indices impairs". Puis on complète cette liste en prenant un chiffre sur deux du numéro de carte bancaire, toujours en le lisant de la droite vers la gauche.

Pour la liste des chiffres "d'indices pairs", on commence par le deuxième chiffre le plus à droite du numéro de la carte de crédit, on se déplace de la droite vers la gauche comme pour la liste précédente et on construit la liste, en prenant un chiffre sur deux. Pour les nombres de cette liste des indices pairs, on double tous les chiffres. Si un nombre est supérieur à 9 , on réalise la somme des deux chiffres qui le composent (exemple si on obtient 16, on additionne 1 et 6 pour avoir 7). Par conséquent, tous les nombres des deux listes sont

composés uniquement de chiffres compris entre 0 et 9 . On calcule alors la somme totale des chiffres de ces deux listes. Si cette somme est un multiple de 10, alors le numéro de la carte de crédit est valide.

Exemple : soit 4762 un nombre (on se limite à 4 chiffres mais le raisonnement est identique pour un nombre à 16 chiffres). Appliquons-lui la formule de Luhn. On commence par le chiffre 2, celui se trouvant le plus à droite. Le nombre 4762 se transforme en deux listes correspondant aux indices impairs et pairs soit [2, 7] et [6, 4]. Puis en deux autres listes, la liste des indices impairs inchangés [2,7] et la liste des indices pairs doublés [12, 8]. La somme des éléments de ces deux listes est égale à 20 car la liste des indices pairs

se réduit en la liste

du fait de la sommation des chiffres constituant le nombre 12. La somme des éléments des deux listes obtenues [2,7] et [3,8] est bien égale à 20. Ce résultat est un multiple de 10 , le nombre 4762 est donc correct au sens de l'algorithme de Luhn.

On aurait pu raisonner sur une seule liste et obtenir le même résultat. 4762 se transforme en la liste [8, 7, 12, 2] puis en la liste [8, 7, 3, 2] après réduction. La somme des chiffres

est égale à 20 .
Q5. Écrire une fonction num_en_liste qui transforme un nombre entier en une liste de chiffres. Cette fonction a un paramètre de type int et retourne un élément de type list.

Exemple:

num_en_liste(4532015112830465)
[4, 5, 3, 2, 0, 1, 5, 1, 1, 2, 8, 3, 0, 4, 6, 5]

Q6. Écrire une fonction tuple_pairs_impairs qui détermine un tuple représentant la liste des chiffres d'indice pair et la liste des chiffres d'indice impair d'un numéro de carte de crédit. Le chiffre le plus à droite de ce numéro est considéré comme le premier chiffre d'indice impair. Cette fonction a un paramètre de type int et retourne un tuple composé de deux éléments de type list.
Exemple :

tuple_pairs_impairs(4532015112830465)
([6, 0, 8, 1, 5, 0, 3, 4], [5, 4, 3, 2, 1, 1, 2, 5])

Q7. Écrire une fonction cree_dico qui, à partir d'un numéro de carte de crédit, crée un dictionnaire avec deux clés nommées 'pair' et 'impair'. La clé 'pair' est constituée de la liste des nombres d'indice pairs du numéro de la carte de crédit et la clé 'impair' de la liste des nombres d'indice impairs.

Exemple:

>>> cree_dico(4532015112830465)
{'pair': [6, 0, 8, 1, 5, 0, 3, 4], 'impair': [5, 4, 3, 2, 1, 1, 2, 5]}

Q8. Écrire une fonction traitement_nb_pairs qui multiplie par 2 tous les chiffres de la liste associée à la clé 'pair'. Si un chiffre est supérieur à 9 , il faut réaliser la somme des deux chiffres qui le composent. Cette fonction a un paramètre de type dictionnaire et retourne un dictionnaire.
Remarque : la partie correspondant à la clé 'impair' n'est pas modifiée par le traitement de cette fonction.

Exemple:

>>> un_dico=cree_dico(4532015112830465)
>>> traitement_nb_pairs(un_dico)
{'pair': [3, 0, 7, 2, 1, 0, 6, 8], 'impair': [5, 4, 3, 2, 1, 1, 2, 5]}

Q9. Écrire une fonction test_num_carte_credit qui utilise l'algorithme de Luhn pour savoir si un numéro de carte de crédit est correct. Vous devez utiliser la fonction traitement_nb_pair pour sa réalisation. Cette fonction a un paramètre de type int et retourne une valeur de type bool.

Exemple :

test_num_carte_credit(4532015112830465)
True

Partie III - Tests de QR code

Les QR codes ont été inventés en 1994, par Masahiro Hara, un ingénieur de l'entreprise japonaise Denso-Wave. Cette invention a permis d'assurer le référencement des pièces détachées dans les usines Toyota. Les QR codes sont constitués essentiellement de pixels noirs et blancs codés dans le format RGB (annexe 1). Cependant, il existe des QR codes bicolores mais avec un jeu de couleurs très contrastées. Les QR codes peuvent être partiellement raturés ou déchirés car un de leurs avantages est qu'ils peuvent accepter un certain taux d'erreurs, entre

suivant la version du QR code. Il existe 40 versions qui peuvent stocker entre 10 et 7089 caractères numériques. Nous nous restreignons ici à la version 1 qui utilise une matrice de

pixels pour sa représentation.

En fait sur la figure 1, l'image du QR code correspond à u ne m atrice de

pixels (programme P1), alors que la matrice initiale d'un QR code de version 1 ne compte que

pixels. Pour qu'un QR code soit plus visible, on a créé la notion de module qui correspond à un bloc de pixels identiques pour représenter un pixel du QR code initial. C'est un mécanisme de zoom pour que le QR code soit visible. Un module a une taille de 2020 pixels. Chaque module représente globalement une valeur binaire : 1 pour le blanc et 0 pour le noir. Attention : ne pas confondre la taille d'un QR code (ici, 420420) avec la taille d'un module (ici, 2020 ) [la valeur 420 correspond à 2120]. Enfin, un QR code est constitué de différents éléments : des motifs de positionnement ( 3 blocs de

pixels), des motifs de synchronisation (6 zones blanches de séparation et 11 pixels de couleur blanc et noir), des motifs de format d'information et une zone comprenant les données utilisateurs avec des motifs de correction (figure 2).

Dans la suite de cette partie, nous n'utiliserons que les QR codes de version 1.

Figure 1 －QR code version 1

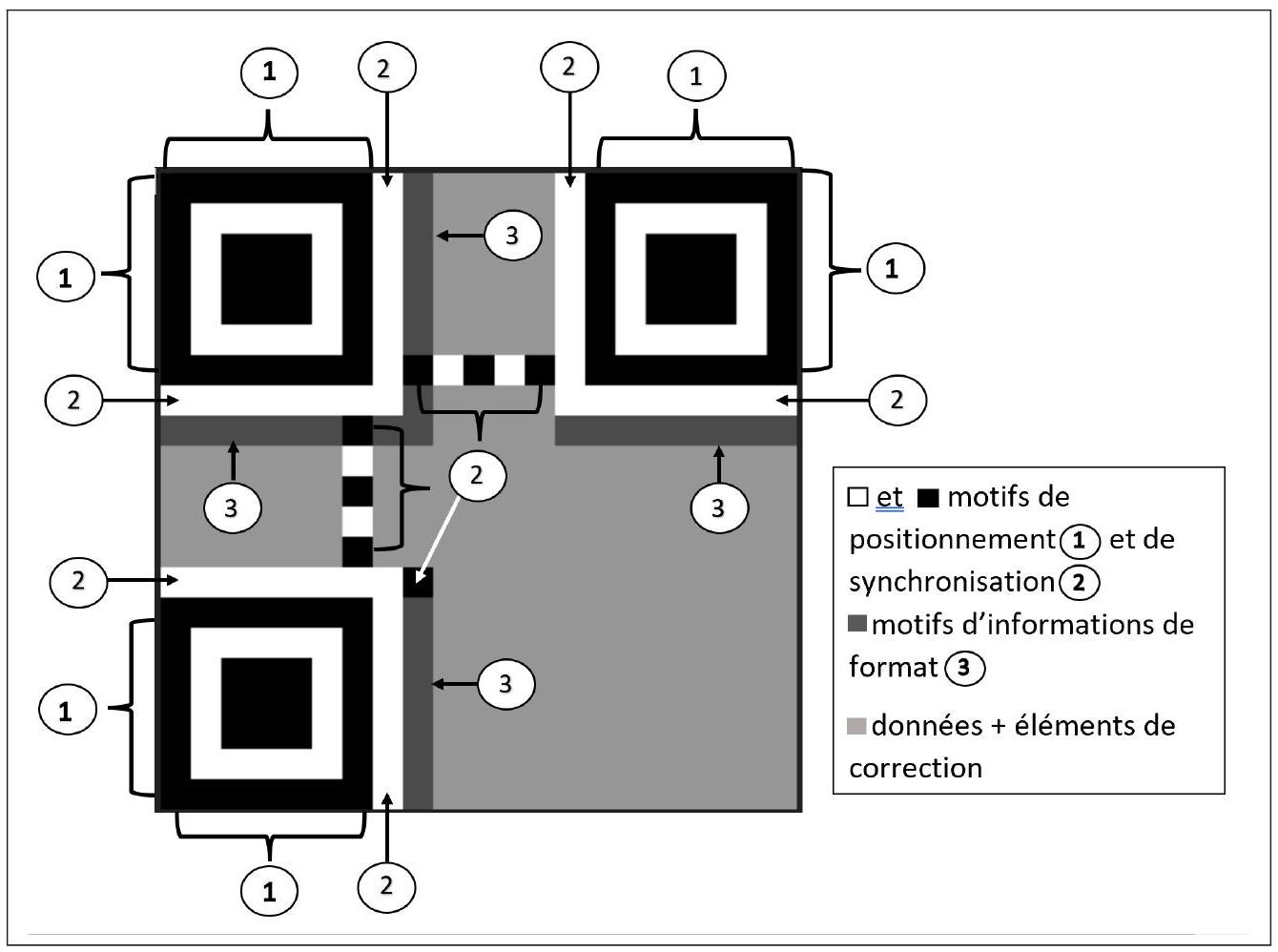
Figure 2 －Organisation d＇un QR code

Q10．Écrire une fonction init qui réalise l＇initialisation d＇une liste de dimension

où chaque élément est également une liste de dimension

．Cette liste de listes représente ainsi une matrice de taille

．Cette fonction a un paramètre de type int et retourne une liste de listes qui représente un QR code initialisé avec des valeurs 0.
Exemple ：

>>> init(4)
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]

On donne le programme P1 suivant : (annexe 1 pour la description du module Gestion_QRCode).

P1
1 from Gestion_QRCode import *
2
3 img=open("./Image/ccinp.png")..........# Lecture de l'image
4 img.show().....................................# Affichage de l'image (figure 1)
5 largeur,hauteur=img.size..................# La taille de l'image (largeur, hauteur)
6 position = (largeur,hauteur) .............# Résultat : (420, 420)

Q11. Écrire la fonction charge_valeur qui a pour but de réduire les données de l'image dans une liste de listes de dimension 2121. Attention : l'image correspondant à un QR code représente une liste de listes de dimension 420420 dont on veut réduire tous les blocs constitués de 20*20 pixels à un seul pixel pour avoir à partir de l'image une liste de listes de dimension

. Ne pas oublier que tous les pixels d'un bloc sont identiques. Cette fonction a un paramètre de type image et retourne une liste de listes de triplets (couleur des pixels).
Indication : utiliser la fonction getpixel du module Python Gestion_QRCode (voir sa définition dans l'annexe 1).
On prend comme bloc de positionnement celui représenté dans la figure 3.

Figure 3 - Bloc de positionnement

Q12. Écrire une fonction cree_bloc qui crée un bloc de positionnement. Cette fonction, qui n'a pas de paramètre, retourne une liste de listes de dimension

.
Exemple :

    >>> cree_bloc()
[[0, 0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 1, 1, 0],
    [0, 1, 0, 0, 0, 1, 0],
    [0, 1, 0, 0, 0, 1, 0],
    [0, 1, 0, 0, 0, 1, 0],
    [0, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 0, 0, 0, 0]]

Q13. Écrire une fonction test_bloc qui teste si un bloc de positionnement (rappel : il y en a trois) est bien représenté pixel par pixel dans un QR code. Cette fonction a 3 paramètres : les coordonnées

donnant la position du début d'un bloc de positionnement d'un QR code (toujours les coordonnées du pixel le plus haut et à gauche) et la liste de listes de dimension 21*21 associée au même QR code. Cette fonction retourne un booléen.
Remarque : on cherche à tester si un bloc de positionnement d'un QR code n'a pas subi une modification. Les coordonnées du pixel le plus haut et à gauche pour le premier bloc sont égales à

, pour le second bloc à

et pour le troisième bloc à ( 14,0 ).

Exemples:

test_bloc( 0,0 , mat1)
True

test_bloc(1,3, mat1)
False
Q14. On considère qu'un QR code est bien positionné lorsque ses 3 blocs de contrôle sont effectivement présents en haut à gauche, en haut à droite et en bas à gauche (comme sur la figure 1). Écrire une fonction test_QRcode qui permet de tester si un QR code est bien positionné. Cette fonction a pour paramètre une matrice de dimension 21 *21 et retourne un booléen.

Exemple :

test_QRcode(mat1)
True

Lors de la lecture d'un QR code par un appareil dédié (scanner, caméra ou autre) le processus de lecture permet de placer un QR code dans l'une des quatre positions possibles, comme illustré dans la figure 4. Cela dépend bien évidemment de l'orientation du QR code lors de sa lecture.

On se propose de faire tourner un QR Code par rotation successive de

afin qu'il puisse se trouver dans la bonne position comme celui de la figure 1.

Figure 4 - Les 4 positions possibles lors de la lecture d'un QR code

Q15.
Écrire une procédure

tourHoraire qui réalise une rotation de

, dans le sens des aiguilles d'une montre, des 4 éléments du QR code. La fonction a trois paramètres, les coordonnées

d'un élément de la liste de listes et une liste de listes de dimension 21*21.

Exemple :

>>> tourHoraire(0,1, mat1)

On se limite à un exemple d'une liste de listes de dimension 4*4 pour expliquer le fonctionnement, mais ce serait la même chose pour une liste de listes de dimension 21 *21. Si on prend les 4 éléments (

) de la liste de listes table 1 de la figure 5 ,

doit se trouver, après une rotation de

, à la place de l'élément

, l'élément

à la place de l'élément

, l'élément

à la place de l'élément

et l'élément

à la place de l'élément

. Le résultat de la transformation est illustré dans la table 2 de la figure 5. Le mécanisme doit s'exécuter de la même manière sur les autres éléments de la table 2. Le résultat de la transformation finale est illustré dans la table 3 de la figure 5.

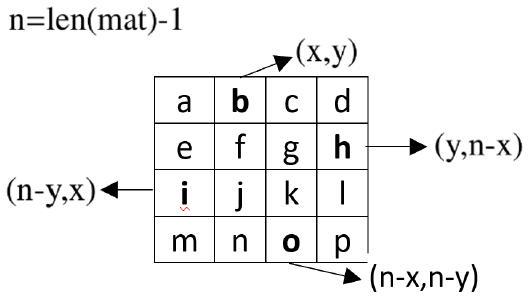
Table 1

a	i	c	d
e	f	g	b
o	j	k	l
m	n	h	p

Table 2

Table 3

Figure 5 - Simple rotation

Q16. Écrire la procédure rotationHoraire qui réalise la rotation de

d'un QR code. Cette procédure a un seul paramètre, une liste de listes de dimension

.
Par exemple, dans la figure 4 cette fonction réalisera la première rotation de

du QR code.

Q17. Connaissant les 4 positions possibles lors de la lecture d'un QR code par un appareil dédié, écrire la procédure QRcode_posi qui positionne correctement un QR code. Cette procédure a un seul paramètre, une liste de listes de dimension 21*21. Indication : utiliser les fonctions rotationHoraire et test_QRcode .

Partie IV - Gestion réseau

Cette entreprise possède de nombreux magasins dans le monde entier. Des serveurs ont été placés dans tous les pays et sont nommés par des lettres.

Les différentes informations envoyées dans le réseau circulent de serveur en serveur. Les serveurs sont représentés par des nœuds, figure 6, et plusieurs routes sont possibles entre chacun d'eux. Le poids associé aux arêtes correspond à la valeur du temps de transmission entre deux nœuds du graphe multiplié par un facteur correctif. L'entreprise souhaite optimiser les temps de transmission entre deux nœuds du réseau en utilisant l'algorithme de Dijkstra.

L'algorithme de Dijkstra permet de déterminer les plus courts chemins à partir d'un sommet unique

vers les autres sommets d'un graphe pondéré orienté ou non

, avec

un ensemble de sommets et

un ensemble d'arêtes qui sont des paires de sommets. Toutes les arêtes de

sont de poids positif.

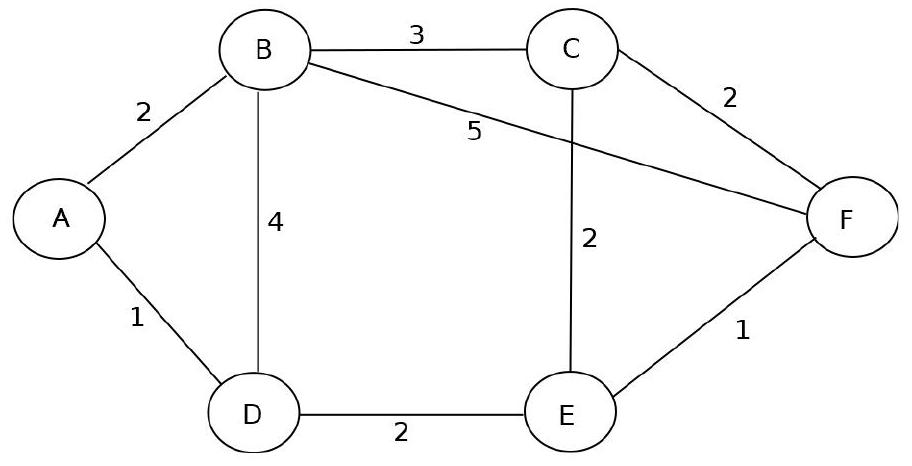
Figure 6 - Organisation des serveurs

Principe de l'algorithme de Dijkstra

Entrée :
    $G(S, A)$ : un graphe pondéré,
            $d$ : le sommet de départ à partir duquel on veut déterminer les plus courts chemins aux
                autres sommets,
            $P$ : construction d'un sous-graphe tel que la distance entre un sommet de $P$ depuis $d$ soit
                définie et soit un minimum dans le graphe $G$,
    Parent : tableau pour noter les sommets par où on passe. Parent est utilisé comme le tableau
                des précédents de chaque sommet, initialisé avec un élément n'appartenant pas à $S$,
            $M$ : tableau où les indices représentent les sommets du graphe : 0 désigne le sommet
                " $A$ ", 1 désigne le sommet " $B$ ", 2 désigne le sommet " $C$ ", etc...
                Les éléments de ce tableau sont corrigés au fur et à mesure de l'algorithme afin
                d'obtenir les distances les plus courtes du sommet de départ à un sommet du graphe.
Début:
        $\mathrm{P} \leftarrow \emptyset$
        $\mathrm{M}[\mathrm{d}] \leftarrow 0 \quad / /$ la distance de $d$ à lui-même est égale à 0
        $\mathrm{M}[\mathrm{s}] \leftarrow+\infty$ pour chacun des sommets du graphe autre que $d$
        Tant qu'il existe un sommet qui ne soit pas dans $P$
                Choisir un sommet $s$ hors de $P$ de plus petite distance $M[s]$
                Ajouter $s$ à $P$
                Pour chaque sommet $u$ hors de $P$ mais voisin de $s$
                    si M[u] > M[s] + poids(s,u)
                        $\mathrm{M}[\mathrm{u}]=\mathrm{M}[\mathrm{s}]+$ poids $(\mathrm{s}, \mathrm{u})$
                        Parent $[u]=s \quad / /$ le sommet $s$ est le prédécesseur du sommet $u$
                Fin du pour
        Fin tant que
Fin

En utilisant l'algorithme de Dijkstra, on souhaite déterminer tous les plus courts chemins, en terme de temps de communication, en partant du sommet

du graphe de la figure 6.

II est plus simple de réaliser l'exécution de l'algorithme de Dijkstra avec un tableau particulier que l'on nomme

. Ce tableau est dans le

. Une première colonne précise l'évolution des distances d'un sommet spécifique depuis le sommet de départ lors de l'exécution de l'algorithme. Chaque ligne correspond à une étape de l'algorithme. Chaque ligne donne les valeurs des distances courantes des sommets depuis le sommet de départ avec éventuellement une mise à jour si une distance est plus petite que celle déjà calculée.

Dans le tableau

, l'élément

correspond à la colonne choisie qui est

, à la valeur 2 du chemin et au sommet précédent

. Sur la ligne de l'élément

on choisit la valeur (3) de la colonne

pour l'étape suivante.
Q18. Compléter les 3 lignes manquantes du tableau

sur le

.
Q19. Donner la valeur du plus court chemin entre "A" et "F". Expliquer comment on obtient cette valeur à l'aide du tableau

. Expliciter le chemin le plus court trouvé pour aller de "

" à "

Partie V - Requêtes SQL

L'entreprise possède une base de données nommée Gestion_Entreprise constituée de trois tables : clients, produits et ventes. Les contenus de ces tables se trouvent en annexe 2.
La table "clients" est constituée de 5 champs :

id : de type INTEGER - clé primaire auto-incrémentée ;
num_secu : de type INTEGER - entier de 15 chiffres ;
nom : de type TEXT;
prenom : de type TEXT;
num_CB : de type INTEGER.

La table "produits" est constituée de 5 champs :

id : de type INTEGER - clé primaire auto-incrémentée ;
ref_produit : de type INTEGER ;
nom_produit : de type TEXT;
qrcode : de type TEXT;
prix : de type DECIMAL.

La table "ventes" est constituée de 3 champs :

date : de type TEXT ;
ref_produit : de type INTEGER ; - clé étrangère, pointe vers la clé primaire id de la table produits;
num_client : de type INTEGER; - clé étrangère, pointe vers la clé primaire id de la table clients.

Les dates dans cette table sont définies par une chaîne de 10 caractères suivant le format année-mois-jour. Exemple de dates : "2019-06-01", "2022-12-30".
Q20. Écrire, en SQL, la requête (1) qui permet d'obtenir le numéro de carte de crédit de toutes les personnes référencées dans la base de données de l'entreprise dont le numéro de sécurité sociale commence par 2. On utilisera le caractère "_" comme le séparateur des milliers. Par exemple 10000000 sera réécrit comme 10_000_000.

Q21. Écrire, en SQL, la requête (2) permettant d'obtenir le nom et le prénom de toutes les personnes ayant effectué un achat avec un résultat sans doublon.

Q22. Écrire, en SQL, la requête (3) qui permet d'obtenir les produits associés à chaque numéro de carte de crédit du client et qui ont été vendus entre le 1 juin 2020 et le 30 juillet 2020. On rappelle que SQL compare les variables de type TEXT grâce à l'ordre lexicographique : par exemple "13-06-1989 < 13-07-1999" est vrai.

Annexe 1

Module "Gestion_QRCode"

fonction Gestion_QRCode.open(fp)

Paramètre :

fp : nom de fichier (chaîne de caractères) représentant une image sous différents formats tels que PPM, PNG, JPEG, GIF, TIFF et BMP.

Retour :

retourne une variable qui est un descripteur d'image (un objet image).

Attention : la valeur retournée n'est en aucun cas une liste de listes ou une liste de listes similaire à celle de la bibliothèque Numpy.

Exemple :
img=Gestion_QRCode.open("uneImage.png")

fonction Gestion_QRCode.Show()

Retour :

retourne la valeur None.

Cette fonction affiche l'image dans n'importe quelle visionneuse d'images.

Exemple:

img.show()

attribut Gestion_QRCode.size

Permet de connaître la taille de l'image en pixels, le résultat est un tuple (largeur, hauteur).
Exemple :
print(img.size)

(360, 160) # soit largeur = 360 pixels et hauteur = 160 pixels

fonction Gestion_QRCode.getpixel(x,y)

Paramètres :

x : la coordonnée x du pixel référencé ;
y : la coordonnée y du pixel référencé.

Retour:

retourne les attributs de la couleur du pixel, au format RVB

La valeur retournée est un tuple (

) correspondant à la couleur du pixel : le plus souvent

pour un pixel noir et

pour un pixel blanc pour un QR code.

Exemple:
(r,v,b) = img.getpixel(100,30)

pour un pixel noir
6. La valeur None est une valeur qui correspond à l'absence de valeur.
7. Le système RVB (Rouge, Vert, Bleu), ou en anglais RGB (Red, Green, Blue), permet de coder les couleurs en informatique. Un écran informatique est composé de pixels représentant une couleur au format RVB. La composante R est codée sur 8 bits de 0 à 255 en décimal. Il en va de même pour les composantes suivantes. Le codage des couleurs va du plus foncé au plus clair.

Annexe 2

Base de données "Gestion_Entreprise"

Le contenu des tables clients, produits et ventes de la base de données Gestion_Entreprise est donné ci-après.

Table "clients"

id	num_secu	nom	prenom	num_CB
1	286128817863441	Eldyn	Sophie	6767342589219928
2	298082934500890	Gomez	Maria	2324563490665454
3	298082934500896	Ruiza	Flor	9889454573204522
4	109086723487917	Kovitz	Boris	6789543778653678
5	175105642102321	Mottreff	Erwan	4745342178563217
6	189027511732543	Settin	Michel	7856432167453492
7	191017511318196	Valérie	Georges	8787564521392354

Table "produits"

id	ref_produit	nom_produit	qrcode	prix
1	27	Buffet chêne		320
2	102	Chaise rustique		65
3	453	Table ronde		75
4	756	Table ovale		120
5	921	Coffret Bali		170

Table "ventes"

date	ref_produit	num_client
2020-05-15	2	2
2020-06-17	3	1
2020-06-21	3	7
2020-07-19	4	5
2020-08-19	5	5
2020-09-05	4	6

Annexe 3

Rappels des syntaxes en Python

Définir une liste.

Définir une liste de listes.

>>> LL[1] [3,4]

Ajouter un élément à la fin d'une liste.

L.append(5) LL.append([9, 10])

Convertir un nombre entier en une chaîne de caractères.

>>> str(12345) '12345'

Convertir une chaîne de caractères en un nombre entier.

Attention : si la chaîne de caractères contient un espace, l'appel de la fonction int provoque une erreur.

>>> int('12345') 12345

donne le quotient de la division euclidienne de

par

>>> 10//3 3

donne le reste de la division euclidienne de

par

>>> 10%3 1

Définir une chaîne de caractères.

mot='Python'

Longueur d'une chaîne.

len(mot)

Le slicing permet d'extraire des éléments d'une liste ou d'une chaîne.

FIN

DOCUMENT RÉPONSE

Seul ce document est à rendre dans son intégralité.

Q1. Fonction num_secu

Q2. Fonction clef

Q3. Fonction num_secu_complet

Q4．test＿num＿secu

｜

Q5．Fonction num＿en＿liste

－

．

－

｜

－

｜

－

｜

－

｜

－

｜

－

0.1

－

－ 0.000

－

－ 0.0 .00

－

－

0.00 .0

－

0.00000

－

｜ 0.00

Q6．Fonction tuple＿pairs＿impairs

－

－

｜

－

｜

－

｜

－

｜

－

｜

－

－

都鎄

－

都讍

－

Q7. Fonction cree_dico

Q8. Fonction traitement_nb_pairs

	-	-	-	-	-	-	-	-	-	-	lo		-	-	-	-	\|	-	-	-	\|	-	-	-	.	-	-	-	-	\|	\|
-	-		-	-		-		-			-	-			-	-	-		-							-					-
	-





	0.00000

Q9. Fonction test_num_carte_credit

Q10. Fonction init

Q11. Fonction charge_valeur

Q12. Fonction cree_bloc

Q13. Fonction test_bloc

Q14. Fonction test_QRcode

Q15. Fonction tourHoraire

Q16. Fonction rotationHoraire

Q17. Fonction QRcode_posi

Q18．Compléter les 3 lignes manquantes du tableau

	A	B	C	D	E	F
étape initiale	0
	－	2		（1）
	－	（2）		－	3
	－	－	5	－	（3）	7

Q19．Donner et expliquer la valeur obtenue du plus court chemin entre＂

＂et＂

＂． Expliciter le chemin le plus court entre＂

＂et＂

＂．

類－

颣

－

類

，

－

，

－

｜

都

－

都

｜

－

｜

－

．

－

Q20. Requête 1

Q21. Requête 2

Q22. Requête 3

1. L'algorithme de Luhn, ou code de Luhn, ou encore formule de Luhn est aussi connu comme l'algorithme "modulo 10".
1. Une procédure est une fonction qui retourne la valeur None mais cette valeur n'est pas destinée à être utilisée ou à être capturée.