ÉPREUVE MUTUALISÉE AVEC E3A-POLYTECH ÉPREUVE SPÉCIFIQUE - FILIÈRE MP

INFORMATIQUE

RAPPEL DES CONSIGNES

• Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
• Ne pas utiliser de correcteur.
• Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont interdites

Partie I - Logique et calcul des propositions

I. 1 - Définitions

• On appelle minterme toute formule de la forme où pour tout est un élément de .
• On appelle maxterme toute formule de la forme où pour tout est un élément de .

• On appelle forme normale conjonctive de toute conjonction de maxtermes logiquement équivalente à .
• On appelle forme normale disjonctive de toute disjonction de mintermes logiquement équivalente à .

I. 2 - Le connecteur de Sheffer

Partie II - Le problème de Freudenthal (Informatique pour tous)

• Pierre: "Je ne connais pas les nombres x et y."
• Sophie : "Avant même que tu me le dises, je savais déjà que tu ne connaissais pas x et y."
• Pierre : "Ah! eh bien maintenant je connais x et y."
• Sophie : "Très bien, mais moi aussi alors maintenant je connais x et y."

• il existe deux sommes et dans la liste Candidat_S(n) telles que ;
• apparaît dans les listes et .

Partie III - Mots de Lyndon et de de Bruijn

III. 1 - Mots de Lyndon

III.1.1 - Définitions

• (valeur du caractère)
• l'opérateur de concaténation ^
• la fonction String.length : string -> int String. length retourne la longueur de .
• la fonction String.sub : string -> int -> int -> string.

• est le concaténé de et .
• est un préfixe de si et pour .
• est un suffixe de si et pour .

III.1.2 - Génération de mots de Lyndon

Algorithme 1 : Algorithme de génération d'un mot de Lyndon
Données : $\mathbf{m} \in \Sigma^{*}$ un mot de Lyndon, $n \geq|m|$
Résultat : $\mathbf{q}$ le mot de Lyndon généré à partir de $\mathbf{m}$.
*** Etape 1 ***
Concaténer le mot $\mathbf{m}$ à lui même jusqu'à obtenir un mot $\mathbf{q}$ de longueur $n$. La dernière occurrence de
    m pourra être tronquée pour arriver à un mot de longueur exactement $n$.
*** Etape 2 ***
tant $\mathbf{q u e}$ le dernier symbole de $\mathbf{q}$ est le plus grand symbole de $\Sigma$ faire
    Ôter ce symbole de $\mathbf{q}$.
*** Etape 3 ***
Remplacer le dernier symbole de $\mathbf{q}$ par le symbole qui suit dans $\Sigma$.
retourner q.

III.1.3 - Factorisation de mots de Lyndon

Algorithme 2 : Algorithme de factorisation d'un mot de Lyndon
Données : $\mathbf{m} \in \Sigma^{*}$ un mot de Lyndon.
Résultat : la liste $\mathcal{L}$ des mots de Lyndon décroissants de la factorisation de $\mathbf{m}$.
$\mathcal{L} \leftarrow[]$
$j \leftarrow 1$
$k \leftarrow 0$
tant que $j \leq|\mathbf{m}|$ faire
    si $j=|\mathbf{m}|$ ou $m_{k}>m_{j}$ alors
        $\mathbf{p}=m_{0} \cdots m_{j-k-1}$
        Ajouter $\mathbf{p}$ à $\mathcal{L}$
        Supprimer $\mathbf{p}$ de $\mathbf{m}$
        $k \leftarrow 0$
        $j \leftarrow 1$
    sinon
        si $m_{k}=m_{j}$ alors
            $k \leftarrow k+1$
            $j \leftarrow j+1$
        sinon
            $k \leftarrow 0$
            $j \leftarrow j+1$
retourner $\mathcal{L}$.

III. 2 - Mots de de Bruijn

III.2.1 - Définition

III.2.2 - Graphe de de Bruijn

• est l'ensemble des sommets du graphe;
• est l'ensemble des arcs orientés du graphe.

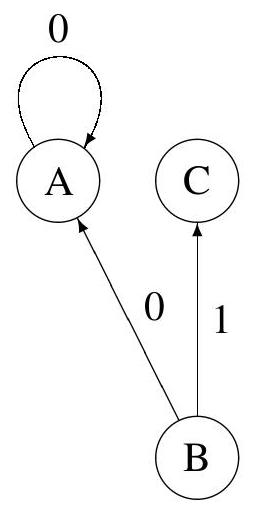
Figure 1 - Exemple de graphe avec boucle sur le sommet A.

III.2.3 - Construction des mots de de Bruijn

III.2.3.1 - Construction à l'aide de

III.2.3.2 - Construction à l'aide de l'algorithme Prefer One

Algorithme 3 : Algorithme Prefer One
Données : $n, \Sigma$
Résultat : $\mathbf{m}$ mot de de Bruijn de longueur $n$ sur $\Sigma$.
$\mathbf{m} \leftarrow$ suite de $n$ zeros
$\mathrm{STOP} \leftarrow$ false
tant que $S T O P=$ false faire
    Etape 1
    Ajouter un 1 à la fin de $\mathbf{m}$.
    si les $n$ derniers symboles de $\mathbf{m}$ n'ont pas été rencontrés auparavant alors
        Répeter Etape 1
    sinon
        Retirer le 1 ajouté à la fin de $\mathbf{m}$.
        Passer à Etape 2
    Etape 2
    Ajouter un 0 à la fin de $\mathbf{m}$.
    si les $n$ derniers symboles de $\mathbf{m} n$ 'ont pas été rencontrés auparavant alors
        Aller à l'Etape 1
    sinon
        $\mathrm{STOP} \leftarrow$ true
retourner m.

III.2.3.3 - Construction à l'aide de la relation aux mots de Lyndon

III.2.4 - Application

• pour la borne supérieure, on considèrera que l'on met bout à bout tous les mots possibles de chiffres construits sur ;
• pour la borne inférieure, on cherchera un mot sans redondance, c'est-à-dire qui contient une et une seule fois chaque mot de chiffres.

• et .
• et .

FIN