N.B. : le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

RAPPEL DES CONSIGNES

Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, bleu clair ou turquoise, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
Ne pas utiliser de correcteur.
Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont interdites.

Le sujet est composé de trois parties indépendantes.

Partie I- Coloration de graphes

L'objectif de cette partie est de proposer une implémentation en Python d'une solution au problème de coloration d'un graphe.

l. 1 - Définitions et propriétés

Soit

un graphe fini non orienté avec

son ensemble de sommets et

son ensemble d'arêtes. On suppose que le graphe est simple c'est-à-dire qu'il ne comporte pas de boucles et que chaque paire de sommets est reliée par au plus une arête. On note

, le cardinal de l'ensemble

. Les sommets sont numérotés de 0 à

. Étant donné un entier naturel

, une

-coloration des sommets de

est une application

telle que pour chaque arête

d'extrémités

. Si

, on considèrera que la couleur

est affectée au sommet

. Si

admet une

-coloration, il est

-coloriable. On définit le nombre chromatique

d'un graphe

fini par

est

-coloriable

.
Une clique est un sous-ensemble de sommets du graphe, adjacents 2 à 2 . On dit qu'un graphe est complet si il est une clique. On notera

le graphe complet à p sommets.
On pose

est une clique de G

, avec

l'ensemble des entiers naturels.

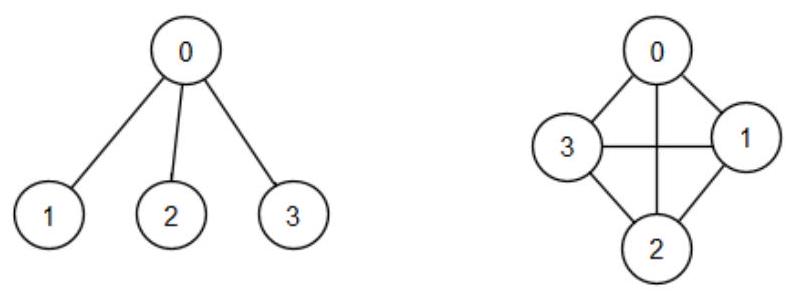
Figure 1 - de gauche à doite, le graphe

et le graphe

Q1. Le graphe

de la figure 1 ci-dessus est-il 2-coloriable ? Justifier votre réponse.
Q2. Pour un entier naturel

, déterminer le nombre chromatique du graphe

.
Q3. Montrer que pour tout graphe

sommets, on a

1.2 - Algorithmique et programmation en Python (Informatique Commune)

La coloration d'un graphe

avec

couleurs est un problème complexe. Dans cette sous-partie, nous présentons une heuristique permettant de construire une coloration d'un graphe donné.
Dans la suite, on implémente un graphe par un dictionnaire (type dict en Python), contenant les listes d'adjacence des sommets. Les clés du dictionnaire sont les numéros des sommets et la valeur correspondant à la clé i du dictionnaire est la liste d'adjacence du sommet numéro i. Notons qu'il serait ici possible d'implémenter le graphe par des listes d'adjacence dans un tableau, dans la mesure où les sommets sont numérotés de 0 à

Q4. Définir en Python le dictionnaire d1 correspondant au graphe

.
Q5. Écrire une fonction Python degres_sommets(d) qui prend en paramètre un dictionnaire

représentant un graphe et renvoie une liste de couples (di,i), i étant le numéro d'un sommet parcourant l'ensemble

et di le degré du sommet i .

Q6. On suppose qu'on dispose d'une fonction Python tri (1) qui trie une liste de couples 1 dans l'ordre décroissant par rapport à la première composante du couple. En déduire une fonction tri_degres (d) qui prend en paramètre un dictionnaire d représentant un graphe et renvoie une liste contenant les numéros des sommets, triés par degrés décroissants.

Q7. Écrire une fonction Python test

qui prend en paramètre un dictionnaire

représentant un graphe

, un dictionnaire c dont les clés représentent les sommets du graphe

et les valeurs, leurs couleurs. La fonction renvoie True si c est une 2-coloration pour

On considère ci-dessous, l'algorithme de coloriage de Welsh-Powel.

Algorithme 1: Welsh-Powel (coloration de graphe)
Entrée : un graphe G à n sommets
Sortie : liste d'entiers contenant en position i la couleur du sommet numéro i
Début
    Ordonner les sommets selon les degrés décroissants dans une liste li;
    colorie : dictionnaire vide qui à terme, associera à chaque clé i, la couleur du sommet i;
    Tant qu' il reste des sommets à colorier faire
        Chercher dans li le premier sommet non colorié et le colorier avec la plus petite couleur
            c non utilisée ;
        Colorier avec cette même couleur, en respectant leur ordre dans li, tous les sommets
            non coloriés et non adjacents à des sommets de couleur c;
    Fin
    Retourner colorie
Fin

Q8. Que contient colorie si on déroule l'algorithme de coloriage ci-dessus avec le graphe

en entrée?

Q9. Écrire une fonction Python adjacent

qui prend en paramètre un graphe représenté par un dictionnaire

, un dictionnaire dc contenant la couleur des sommets coloriés, le numéro d'un sommet

, une couleur

et renvoie True si le sommet

est adjacent à l'un des sommets de couleur c, False sinon.

Q10. Proposer une implémentation en Python de l'algorithme de Welsh-Powel.

Application

Le tableau ci-dessous représente les liens d'amitiés entre huit étudiants : Alice (A), Béatrice (B), Carl (C), David (D), Eloïs (E), Fanny (F), Gary(G) et Hedge (H).

Prénom
Ami e avec

On souhaite créer des groupes de travail. Dans le contexte de l'application, un groupe contient au moins 2 étudiants tel que chaque étudiant soit dans un groupe différent de celui de ses amis.
Q11. Modéliser la situation par un graphe et en déduire une solution.

Partie II - Satisfiabilité d'une formule propositionnelle

Le langage utilisé dans cette partie est OCaml.

Une formule propositionnelle est construite à l'aide de constantes propositionnelles, de variables propositionnelles et de connecteurs logiques. Les connecteurs logiques seront notés

(négation),

(conjonction),

(disjonction). Dans cette partie, on étudie le problème de satisfiabilité d'une formule et son application à la détermination d'une conséquence logique entre 2 formules propositionnelles. Le problème CNF-SAT est défini de la façon suivante. Étant donné une formule sous forme normale conjonctive, admet-elle un modèle, c'est-à-dire une valuation des variables, qui rende la formule vraie? On souhaite écrire un programme qui teste si une valuation donnée rend une telle formule vraie.
Dans cette partie, on considère que si une formule contient

variables propositionnelles, elles seront désignées par

.
On définit le type OCaml suivant :
type clause=Var of int|Non of clause | Ou of clause*clause
L'argument du constructeur Var correspond au numéro de la variable concernée.
Une formule sous forme normale conjonctive ayant

clauses sera implémentée par une liste de

clauses. Les tableaux seront implémentés par le module Array dont les éléments suivants pourront être utilisés :

type 'a array, notations [| |]
création d'un tableau: make : int -> 'a -> 'a array
accès à l'élément d'indice i du tableau t : t. (i)
modification de l'élément placé à l'indice i du tableau t : t. (i) <- v
taille du tableau: length : 'a array int

Q12. Donner le code OCaml correspondant à la clause

.
Q13. Donner le code OCaml permettant de définir la formule :

.
Q14. Écrire une fonction de signature evalue_clause : clause -> bool array -> bool qui prend en paramètre une clause et une valuation représentée par un tableau contenant à l'indice

, la valeur de vérité de la variable

et renvoie la valeur de vérité de la clause.

Q15. Écrire une fonction de signature evalue_FNC : clause list -> bool array -> bool qui prend en paramètre une clause et une valuation représentée par un tableau contenant à l'indice

, la valeur de vérité de la variable

et évalue une formule donnée sous forme normale conjonctive.

Q16. Quel résultat obtient-on avec la formule

et le tableau de valuations [|false; true; true|]? Justifier.

Q17. On souhaite énumérer toutes les valuations possibles pour un nombre de variables fixé. Étant donné une valuation, on considérera que si la valeur true correspond à 1 et la valeur false correspond à 0 , la valuation suivante correspond à l'ajout de 1 au nombre binaire associé. Ainsi, la valuation suivante de [|false;true;falsel] est [|false;true;true|]. On considère que la valuation suivante de [|true; true; true|] n'existe pas. Écrire une fonction de signature suivant : bool array

bool qui prend en paramètre un tableau de booléens, lui attribue la valuation "suivante" si possible et renvoie true; sinon renvoie false.

Q18. En déduire une fonction de signature satisfiable : clause list

int

bool qui prend en paramètre une formule en forme normale conjonctive, son nombre de variables et renvoie true si il existe une valuation qui rend la formule vraie, false sinon.

Q19. Quelle est la complexité en temps de cette fonction par rapport aux paramètres d'entrée?
Q20. Proposer une stratégie de retour sur trace pour résoudre le problème de satisfiabilité d'une formule.

Conséquence logique entre 2 formules

Définition

Une formule

est une conséquence logique d'un ensemble fini de

formules

étant un entier naturel supérieur ou égal à 1 , si tout modèle de

est un modèle de

. On note

. On admettra que toute formule admet une formule équivalente sous forme normale conjonctive.

Q21. Déduire de la fonction précédente, un algorithme en pseudo-code permettant de déterminer si une formule

est une conséquence logique d'un ensemble de formules

Q22. Afin de déterminer si

, on peut prouver le séquent

. Justifier cette méthode, puis construire un arbre de preuve qui démontre le séquent

où

désignent des variables propositionnelles représentant des formules logiques, à partir des règles d'inférence de la déduction naturelle; les règles et notations utilisées seront clairement mentionnées.

Partie III - Automates et reconnaissance de motifs

Dans cette partie, le langage utilisé est OCaml.

On s'intéresse à la reconnaissance de motifs dans un texte en utilisant une méthode naïve, puis des automates.

III. 1 - Autour de l'algorithme naïf de recherche de caractères

Définitions

Un alphabet

est un ensemble fini non vide d'éléments appelés lettres. Un mot défini sur

est une suite finie d'éléments de

. Le mot vide sera noté

. L'ensemble des mots sur l'alphabet

est noté

. La longueur d'un mot

, notée

est le nombre de lettres de ce mot. Pour i allant de 0 à

désignera la lettre en position

. Ainsi,

est un mot de longueur 3, sur tout alphabet contenant les lettres

.
Un mot

est un facteur d'un mot

si il existe 2 mots

tels que

. Dans ce cas, on dit qu'il y a une occurrence de

dans

. Quand

est un préfixe de

et quand

est un suffixe de

. Soit

un mot non vide. Un entier

est une période de

pour

. On définit la période de

comme étant la plus petite des périodes.
Un bord d'un mot non vide

est un facteur de

, différent de

et qui est à la fois un préfixe et un suffixe de la chaîne de caractères. Par exemple,

, a,aa,aabaa sont les bords du mot aabaabaa. On note

le plus long bord de

. On constate que lorsqu'il est défini, le bord d'un bord d'un mot

est aussi un bord de

. On le note

. On définit ainsi récursivement

avec

un entier naturel.

En OCaml, les fonctions suivantes pourront être utilisées sur le type string:

String. length : longueur de la chaîne de caractères
s. [i] : accès à la lettre d'indice de la chaîne
- : opérateur concaténation

Q23. Justifier le fait que tout mot non vide possède au moins une période.
Q24. Écrire une fonction de signature occurrence : string

string

bool qui prend en paramètre 2 chaînes de caractères x , y et renvoie true si il existe une occurrence de x dans y, false sinon.

Q25. Quelle est la complexité en temps de la fonction occurrence en fonction de la longueur des chaînes de caractères en entrée?

Q26. Déterminer la période du mot

aabaabaa défini sur l'alphabet

.
Q27. Écrire une fonction de signature periode : string -> int qui renvoie la période d'une chaîne de caractères.

Q28. Soit

une chaîne de caractères non vide et

un entier naturel tel que

. Montrer que

est une période de

si et seulement si il existe 3 chaînes de caractères

telles que

Q29. Soit

une chaîne de caractères non vide et

le plus grand entier tel que

est bien défini. On a donc

. Montrer par récurrence sur la longueur des mots que

est la suite des bords de

dans l'ordre décroissant de leur longueur et que

est la suite des périodes de

dans l'ordre croissant.

Q30. Expliquer brièvement comment la connaissance des bords peut permettre d'améliorer la complexité en temps dans le pire cas, de l'algorithme naïf de recherche d'une occurrence d'un mot.

III. 2 - Localisation des occurrences d'un motif à l'aide d'un automate

Un automate déterministe

sur l'alphabet

est composé d'un ensemble d'états finis

, d'un état initial

, d'un ensemble d'états terminaux

et d'une fonction de transitions

. On le désigne par un quintuplet (

). On dit qu'il est complet si

est définie pour chaque élément de

.
Certains automates peuvent être utilisés comme machine de recherche pour le traitement séquentiel de textes. Étant donné un alphabet

, un motif

représente un langage non vide ne contenant pas le mot vide. Le problème de la recherche de motifs est celui de la localisation d'occurrences de mots du langage dans d'autres mots. On suppose qu'on dispose d'un automate déterministe

complet qui reconnaît le langage

, autrement dit, l'automate

reconnaît les mots qui ont comme suffixe un mot de

.
L'algorithme suivant permet de localiser les mots de

reconnus dans un texte

, considéré comme une chaîne de caractères.
Dans la suite, l'automate

de la figure 2 ci-après sera cité en exemple. Il est défini sur l'alphabet

Algorithme 2 : reconnaissance de mots dans un texte
Cherche ( $M, t$ ) ;
Début
    $\mathrm{e} \leftarrow$ initial[M];
    lst $\leftarrow$ liste vide;
    Pour chaque lettre $\lambda$ de $t$ prise dans l'ordre croissant de leurs indices faire
        $\mathrm{e} \leftarrow \delta(\mathrm{e}, \lambda)$;
        Si e est un état terminal alors
            ajouter à lst l'indice de $\lambda$ dans t ;
        Fin
    Fin
    Retourner lst;
Fin

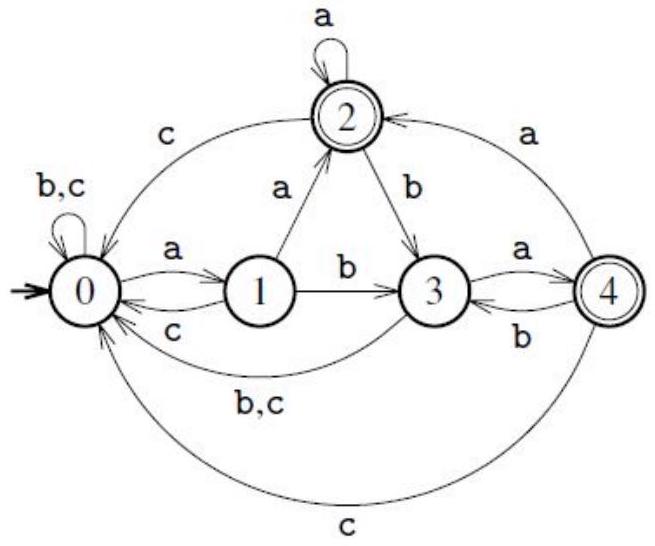
Figure 2 - Automate

On définit en OCaml un type automate par :
type auto={etats: int list; alphabet : char list; initial: int;
transition: int -> char ->int; final : int list}; ;
Q31. Créer une variable automate qui représente l'automate

de la figure 2.
Q32. L' automate

est-il émondé? Justifier.
Q33. Présenter les premières étapes de l'algorithme d'élimination des états appliqué à l'automate

. On éliminera l'état 0 .

Q34. Que représentent les indices mémorisés dans la liste lst de l'algorithme cherche? Que contient la liste 1 de l'algorithme cherche avec l'automate ci-dessus et

cabaac?

Q35. Écrire une fonction de signature cherche : auto -> string -> int list qui implémente l'algorithme cherche.

Q36. Montrer la correction de l'algorithme cherche.