J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

CCINP Physique 1 MP 2005

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ccinp
🔗 Explorer
Banque
CCINP
Année
2005
Filière
MP
Matière
Physique
CCINP MPCCINP 2005MP PhysiquePhysique 2005
2025_09_04_97035f63837e6a3d5d82g

EPREUVE SPECIFIQUE - FILIERE MP

PHYSIQUE 1

Durée : 4 heures

Les calculatrices sont autorisées.

NB : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction.
Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

Conformément à l'usage international, les vecteurs sont représentés en gras.

MECANIQUE

  • Toute réponse non justifiée ne sera pas prise en considération.
  • Toutes les grandeurs physiques seront exprimées en fonction des paramètres du problème (ou des paramètres spécifiés) et simplifiées à l'extrême.
  • Elles seront évaluées numériquement chaque fois que demandé (A.N.).
Pour les applications numériques, on prendra:
Soit un référentiel galiléen , où représente la verticale ascendante. Par rapport à ce référentiel, on considère un disque horizontal en acier, , de rayon et de centre . Le disque peut tourner autour de l'axe vertical passant par son centre et se situe à une hauteur du sol horizontal. On considère le référentiel lié au disque. Le
mouvement de rotation du disque par rapport à est repéré par l'angle , orienté de vers (cf. figure 1). Les axes et sont confondus à l'instant de la mise en mouvement du disque qui sera pris comme origine des temps. Le mouvement donné au disque (à ) est un mouvement de rotation uniformément accéléré, caractérisé par l'accélération angulaire . Le seul champ de forces externe est le champ de pesanteur terrestre que l'on considérera comme uniforme, .
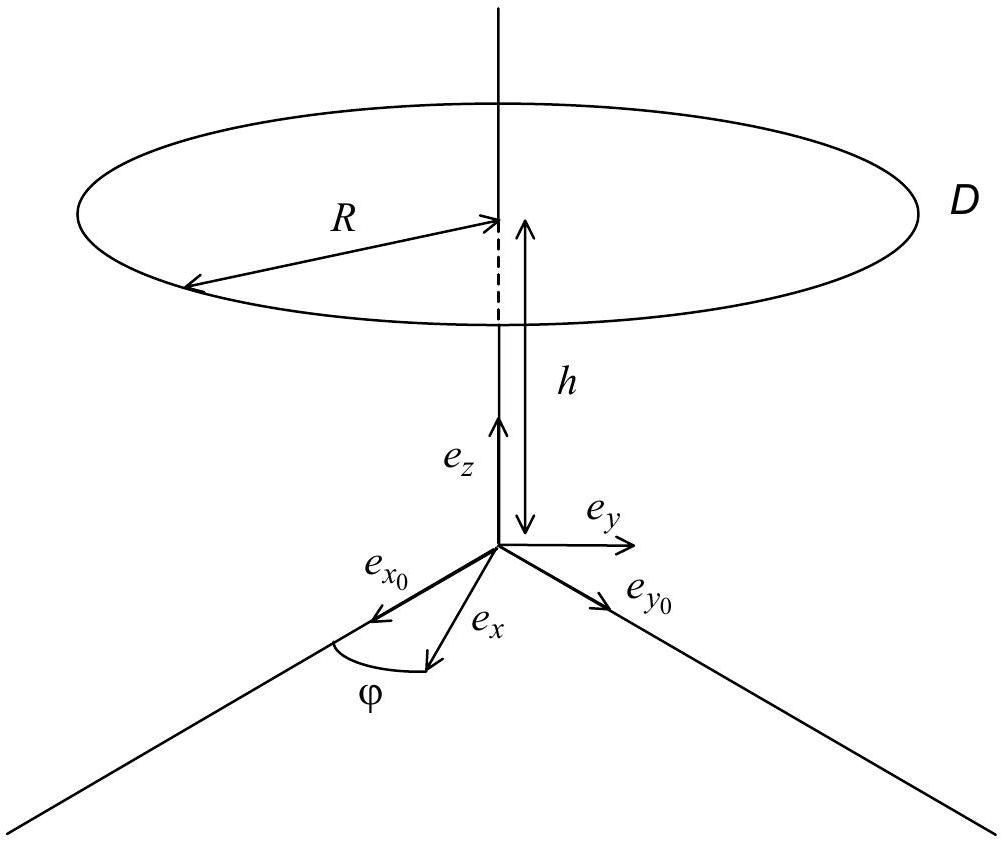
Figure 1

Mouvement d'une pièce de monnaie sur le disque

Le but du problème est l'étude du mouvement d'une pièce de monnaie placée sur le disque.

Une pièce de monnaie en cuivre est posée sur le disque. Elle est assimilée à un point matériel , de masse . Elle est placée sur le disque avant sa mise en mouvement en avec . Le contact entre et est caractérisé par un coefficient de frottement solide statique et un coefficient de frottement solide dynamique .
On note :
  • la force de contact exercée par le disque sur le point .
  • sa composante normale au disque.
  • sa composante dans le plan du disque.

1. Mouvement sur le disque

1.1 Mise en mouvement

On s'intéresse dans cette partie au mouvement de dans , c'est-à-dire, au mouvement de la pièce par rapport au disque.
On note :
1.1.1 Phase précédant la mise en mouvement de la pièce
a. Exprimer et en fonction de .
b. Donner l'expression des forces d'inertie dans . Les exprimer en fonction de et , en supposant immobile dans .
c. Rappeler les lois de Coulomb sur le frottement entre deux solides.
d. Ecrire les équations d'équilibre de dans sa position initiale .
e. Donner la condition pour que soit à l'équilibre.
f. Déterminer l'accélération maximale du disque pour qu'au démarrage (à ) le point reste immobile. A.N.
g. Calculer, en fonction de et du rapport et dans le cas , le temps au bout duquel le point se met en mouvement.
h. Calculer, en fonction de et , la vitesse angulaire de rotation atteinte par le disque lorsque le point se met en mouvement.
i. Calculer de même, l'accélération maximale pour que le point reste immobile pendant au moins une rotation du disque. A.N. : calculer et .

1.1.2 Conditions initiales du mouvement

On suppose désormais, et pour toute la suite, .
a. Montrer qu'alors peut être considéré comme grand devant 1 .
b. En déduire une expression approchée de . A.N.
c. En déduire une expression approchée de . A.N. : calculer .
d. Donner une borne supérieure des erreurs relatives correspondantes : et . A.N.
e. Comparer alors et à l'instant .
f. En déduire la direction approchée initiale du mouvement de et des valeurs initiales approchées et de à et . A.N.

1.2 Mouvement

Dès que le point se met en mouvement, la vitesse de rotation du disque est maintenue constante à la valeur qu'elle avait à ce moment là.

1.2.1 Equations différentielles du mouvement

a. Etablir les équations différentielles exactes du mouvement de vérifiées par et .
b. Calculer, en fonction de et de , l'accélération initiale approchée à . A.N.

1.2.2 Mouvement guidé

A partir de maintenant et pour toute la suite du mouvement sur le disque, la pièce est contrainte à se déplacer suivant .
a. Etablir l'équation horaire du mouvement de . On exprimera et en fonction de , et .
b. Déterminer alors, en fonction de et , l'instant où la pièce arrive au bord du disque. A.N. : calculer pour l'instant d'arrivée au bord et la durée du mouvement .
c. Donner l'expression de l'évolution temporelle de la force de contact . A.N. : la calculer à .
d. Donner une estimation de la limite supérieure du déplacement que la pièce aurait eu à l'instant si le mouvement n'avait pas été guidé. A.N. Conclusion ?

2. Sortie du disque

2.1 On s'intéresse ici aux conditions initiales du mouvement de par rapport au sol (référentiel ).
a. Dans les conditions du mouvement guidé, calculer la vitesse de par rapport à dans la base de . Commenter ce résultat. A.N.
b. Calculer l'angle qu'elle fait avec . A.N. : calculer sa valeur pour (on précisera le nombre de tours complets effectués).
c. Soit la vitesse de par rapport à . Calculer sa norme . A.N.
d. Calculer l'angle qu'elle fait avec l'axe . A.N. : calculer sa valeur pour .
2.2 On désigne désormais par l'instant origine où la pièce quitte le disque. Son point de sortie est choisi comme origine du référentiel du laboratoire: .
Le disque a été accéléré avec une accélération angulaire de telle sorte que la vitesse de à l'instant soit parallèle à et de même sens: avec .
On prendra pour les applications numériques .
a. Déterminer la vitesse en à l'instant où le point entre en contact avec le sol. On donnera sa norme et ses composantes dans . A.N.
b. Calculer la durée de la chute . A.N.
c. Calculer alors la distance horizontale parcourue . A.N.

THERMODYNAMIQUE

L'objectif de ce problème est l'étude du fonctionnement stationnaire d'une machine ditherme de réfrigération.

Le cycle représenté, dans un diagramme de Clapeyron, par la figure 1 constitue un modèle de fonctionnement d'une machine de réfrigération dans laquelle une masse de fluide frigorigène subit les transformations suivantes :
  • : compression adiabatique dans le compresseur.
  • : refroidissement et liquéfaction isobares de la vapeur dans le condenseur.
  • : détente adiabatique et isenthalpique dans le détendeur.
  • : vaporisation isobare dans l'évaporateur.
Les sources froide (intérieur de l'enceinte à réfrigérer) et chaude (milieu ambiant) sont assimilées à des thermostats de températures, respectives, et constantes.
Les variations d'énergie cinétique et d'énergie potentielle du fluide sont négligeables.

Données :



Enthalpies massiques du fluide frigorigène dans les états représentés par les points et :
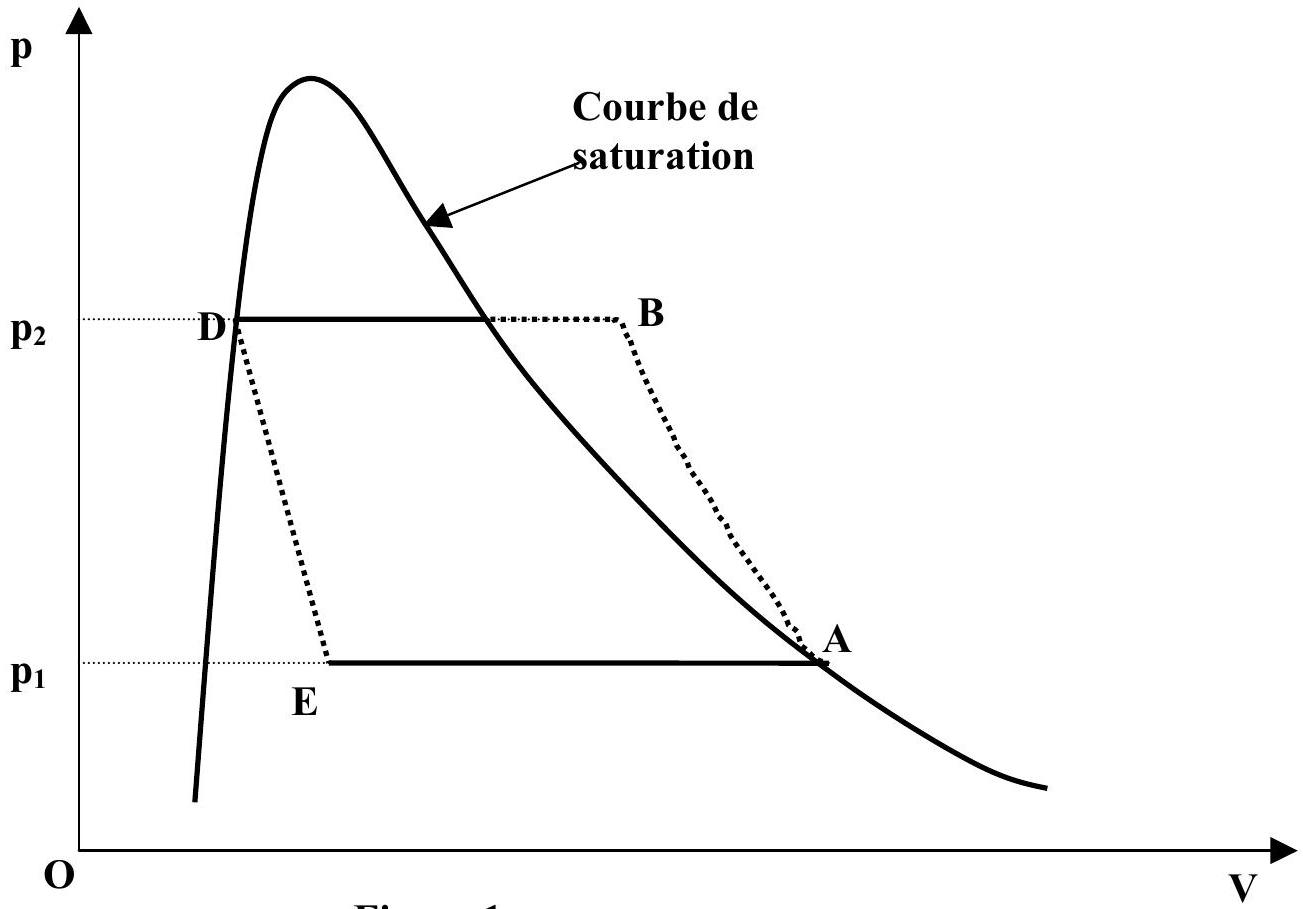
Figure 1

A - Performances de l'installation

A-1 Un système fermé subit une transformation isobare qui le fait évoluer de l'état initial à l'état final . Au cours de cette transformation le système reçoit les quantités d'énergie par transfert thermique et par transfert mécanique (travail).
A-1-1 Appliquer le premier principe de la thermodynamique à cette transformation.
A-1-2 Etablir la relation entre la variation d'enthalpie du système et .
A-2 On désigne par et les quantités d'énergie reçues par le fluide, par transfert thermique, respectivement, au contact de la source froide et au contact de la source chaude, au cours du cycle défini ci-dessus.
A-2-1 Exprimer et en fonction des données.
A-2-2 Calculer et .
A-3 On désigne par l'énergie reçue par le fluide, par transfert mécanique (travail), au cours d'un cycle.
A-3-1 Exprimer en fonction des données.
A-3-2 Calculer .
A-4 On désigne par et les valeurs algébriques des entropies échangées par le fluide, respectivement, avec la source froide et la source chaude au cours du cycle.
A-4-1 Exprimer et en fonction des données.
A-4-2 Calculer et .
A-4-3 Calculer l'entropie créée au cours du cycle. Conclusion.
A-5 Calculer l'efficacité de cette installation.
A-6 Sachant que la puissance à extraire de la source froide pour maintenir sa température constante est de 500 W , calculer le débit massique que l'on doit imposer au fluide frigorigène.

B - Etude de la compression de la vapeur

La vapeur issue de l'évaporateur est comprimée de la pression bar (état ) à la pression bar (état ).
Dans cette partie du problème on admettra que l'on peut assimiler la vapeur à un gaz parfait dont le rapport des capacités thermiques conserve une valeur constante égale à 1,14 dans le domaine étudié.
B-1 On envisage le cas où cette compression pourrait être supposée adiabatique et réversible.
B-1-1 Etablir la relation que vérifieraient les variables température et pression .
B-1-2 Sachant que , calculer la température que l'on atteindrait en fin de compression.
B-2 En réalité la compression subie par la vapeur peut être supposée adiabatique mais n'est pas réversible car on ne peut pas négliger les frottements fluides qui se produisent à l'intérieur du compresseur ; de ce fait la température en fin de compression est supérieure à celle calculée précédemment.
La transformation polytropique est la transformation réversible qui permettrait au fluide d'évoluer de l'état à l'état en recevant, par transfert thermique, une quantité d'énergie équivalente à celle générée par les frottements internes au cours de la transformation irréversible .
Pour établir la loi d'évolution polytropique, on considère une transformation élémentaire réversible caractérisée par les variations d'énergie interne , d'entropie et de volume . La quantité d'énergie reçue par le fluide, par transfert thermique, au cours de cette transformation, s'écrit . Dans cette expression a désigne un facteur qui sera supposé constant dans tout le domaine étudié.
B-2-1 Exprimer en fonction de et .
B-2-2 Montrer qu'au cours de l'évolution polytropique les variables pression et volume vérifient la relation constante dans laquelle désigne une constante appelée facteur polytropique.
B-2-3 Exprimer en fonction de et de .

C-Détermination des conditions de fonctionnement permettant d'obtenir l'efficacité maximale.

C-1 Préciser la nature du cycle réversible que devrait décrire le fluide afin de parvenir à l'efficacité maximale de la machine de réfrigération. On indiquera avec précision la nature et le rôle des différentes transformations subies par le fluide au cours de ce cycle.
C-2 Sachant qu'au cours de ce cycle la variation d'entropie massique du fluide au cours de la transformation qu'il subit au contact de la source chaude est de , calculer les quantités d'énergie et reçues, par transfert thermique, par 1 kg de fluide frigorigène, au cours d'un cycle, respectivement, au contact de la source froide et au contact de la source chaude.
C-3 Exprimer l'efficacité en fonction des températures et et calculer .

D - Etude de la diffusion thermique dans les parois des échangeurs

Les conditions de fonctionnement, idéales et théoriques, définies ci-dessus ne prennent pas en compte l'épaisseur des parois des échangeurs thermiques situés au contact des sources froide et chaude.
Dans cette quatrième partie du problème on se propose de tenir compte de la diffusion thermique à travers les parois des échangeurs. On supposera cette diffusion unidirectionnelle.
On considère la diffusion thermique unidirectionnelle suivant l'axe à travers une paroi plane, homogène et isotrope, d'épaisseur , de surface et de conductivité thermique (figure 2).
En régime stationnaire les faces d'abscisses et sont des surfaces isothermes aux températures et avec .
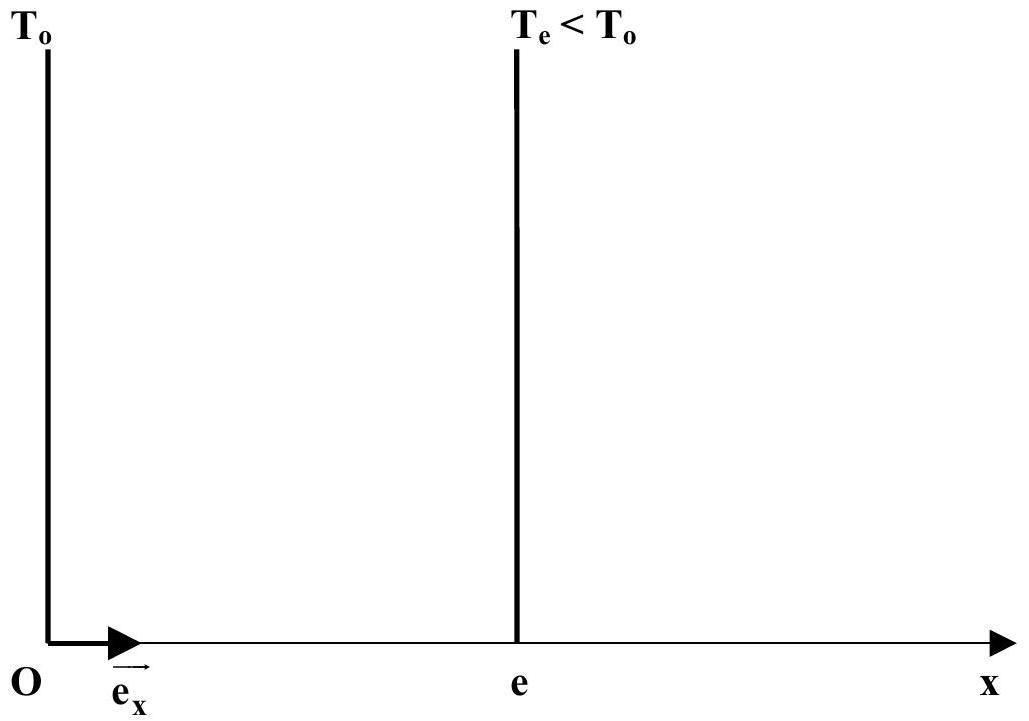
Figure 2
D-1 Rappeler l'expression du vecteur flux thermique surfacique à travers la paroi considérée (loi phénoménologique de Fourier).
D-2 Exprimer le flux thermique à travers cette paroi en fonction des températures et et de la conductance thermique de la paroi.
D-3 Exprimer la durée nécessaire au transfert d'une quantité de chaleur à travers cette paroi. Qu'advient-il si tend vers 0 ?
D-4 On considère de nouveau la machine de réfrigération définie ci-dessus et on suppose que le fluide frigorigène décrit un cycle réversible au cours duquel les transferts thermiques avec les sources froide et chaude se produisent lors de transformations isothermes aux températures respectives et .
On admet que dans les échangeurs thermiques qui assurent les échanges avec les sources de chaleur, la face en contact avec le fluide est à la température du fluide et celle en contact avec la source de chaleur est à la température de cette source.
On désigne par et les conductances thermiques des parois des échangeurs situés, respectivement, au contact de la source froide et de la source chaude.
D-4-1 On désigne, respectivement, par et les quantités d'énergie reçues par le fluide, par transfert thermique, au contact des sources froide et chaude et par et
les durées de transfert de ces quantités d'énergie. Exprimer en fonction de , et et en fonction de et .
D-4-2 Exprimer l'efficacité du cycle décrit par le fluide en fonction de et de .
D-4-3 Sachant que et , calculer .
D-4-4 Exprimer et en fonction de et du travail reçu par le fluide au cours d'un cycle.
D-4-5 Exprimer en fonction de et et en fonction de et .

E-Conditions permettant d'obtenir une consommation minimale

On cherche à déterminer les températures et qui rendent minimale la puissance consommée par la machine au cours d'un cycle. On suppose que la durée des transformations adiabatiques est négligeable devant celle nécessaire aux transferts thermiques.
E-1 Exprimer la puissance moyenne consommée par le fluide au cours d'un cycle en fonction de et .
E-2 On pose et . Exprimer en fonction de et de .
E-3 Déterminer les conditions que doivent vérifier et pour que la puissance consommée soit minimale.
Fin de l'énoncé
CCINP Physique 1 MP 2005 - Version Web LaTeX | WikiPrépa | WikiPrépa