Version interactive avec LaTeX compilé
Les calculatrices sont autorisées.
N.B. : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.
Les candidats doivent respecter les notations des énoncés et préciser, dans chaque cas, la numérotation de la question traitée.
Les candidats doivent respecter les notations des énoncés et préciser, dans chaque cas, la numérotation de la question traitée.
DOSSIER REMIS AUX CANDIDATS
- Le sujet comporte 9 pages
L'épreuve comporte deux problèmes totalement indépendants. Dans chaque problème, de nombreuses questions sont indépendantes.
PROBLÈME A : CAPTEUR DE DILATATION INTERFEROMETRIQUE
Dans ce problème, la lumière se propage dans des fibres optiques à saut d'indice, très fines. On pourra confondre le trajet de la lumière avec l'axe de la fibre.
A. 1 COUPLEUR OPTIQUE
On réalise un coupleur optique en approchant suffisamment deux fibres optiques. Ceci est réalisé actuellement avec des composants à base de semi-conducteurs.
A.1.1 Citer un exemple de matériau semi-conducteur très répandu.
A.1.2 Le schéma de principe du coupleur est donné sur la figure 1.
A.1.1 Citer un exemple de matériau semi-conducteur très répandu.
A.1.2 Le schéma de principe du coupleur est donné sur la figure 1.
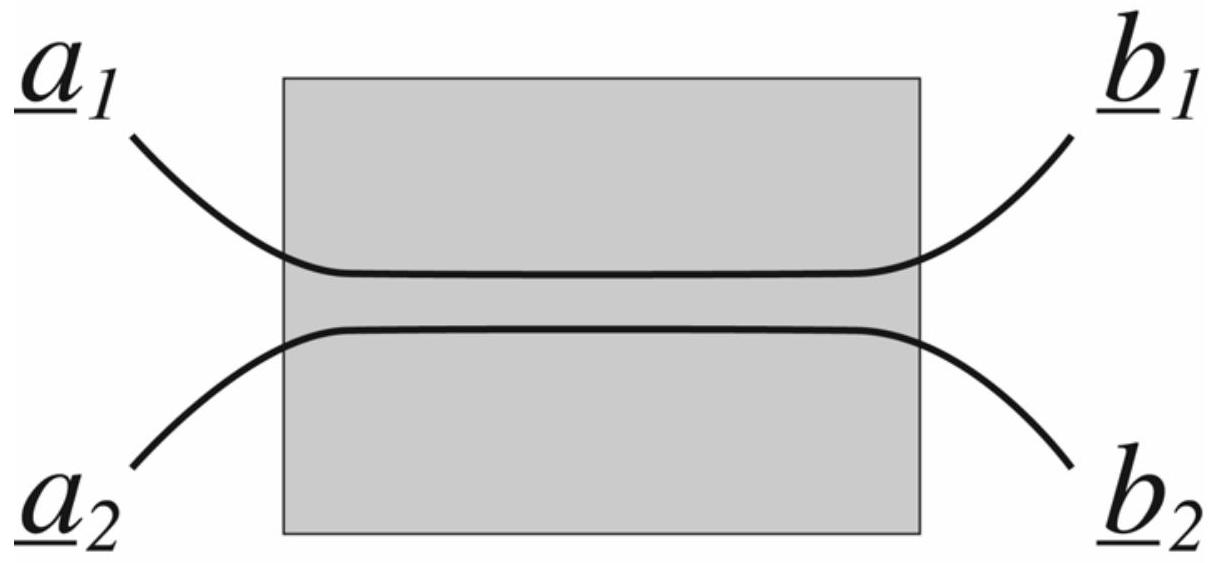
Figure 1 : schéma de principe d'un coupleur optoélectronique
Si
où
Ecrire les amplitudes
A.1.3 Par quel instrument couramment utilisé en optique pourrait-on remplacer ces coupleurs ?
A.1.3 Par quel instrument couramment utilisé en optique pourrait-on remplacer ces coupleurs ?
A. 2 INTERFEROMETRE DE MACH - ZEHNDER ET DETECTION DE DILATATION
Le dispositif est schématisé ci-dessous :
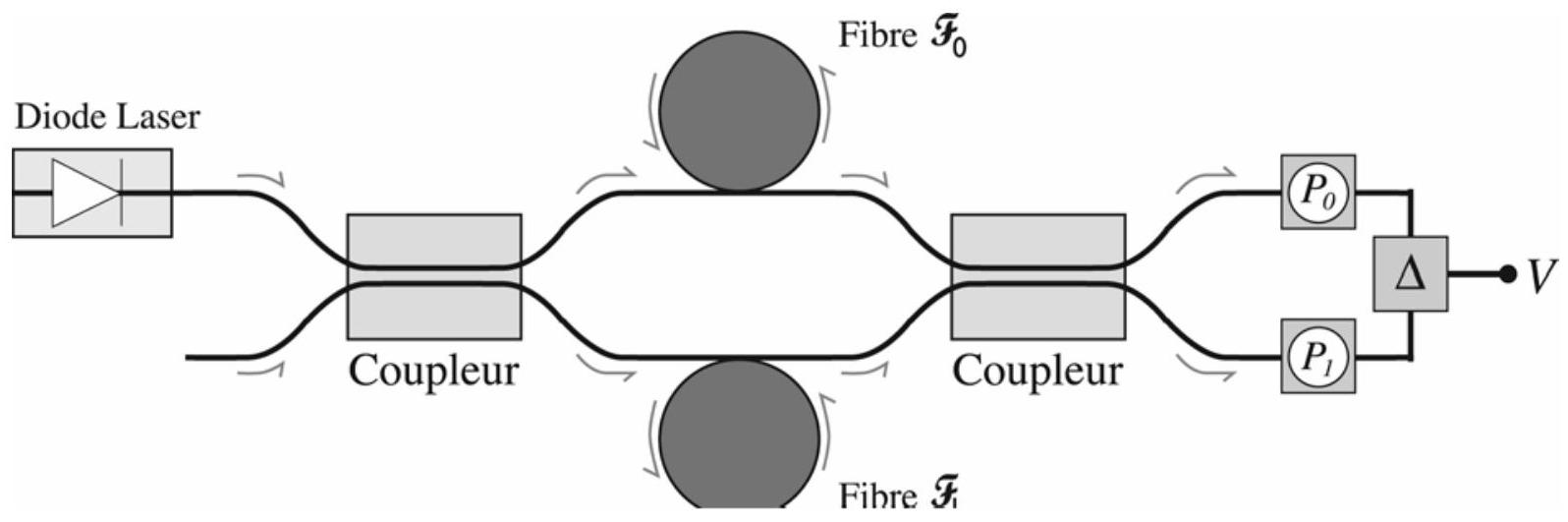
Figure 2 : dispositif de Mach - Zehnder à fibres optiques
Une fibre optique
Une deuxième fibre
A.2.1 A quel domaine du spectre électromagnétique appartient la radiation émise par la diode Laser?
A.2.2 Quelle est l'unité du coefficient
A.2.3 Exprimer les amplitudes
A.2.4 Exprimer alors les intensités
A.2.1 A quel domaine du spectre électromagnétique appartient la radiation émise par la diode Laser?
A.2.2 Quelle est l'unité du coefficient
A.2.3 Exprimer les amplitudes
A.2.4 Exprimer alors les intensités
Des photodiodes
A.2.5 Le dispositif est réglé de telle façon à avoir
A.2.6 Il se peut que le cylindre sur lequel est enroulé la fibre
A.2.5 Le dispositif est réglé de telle façon à avoir
A.2.6 Il se peut que le cylindre sur lequel est enroulé la fibre
A.3. REALISATION DES CIRCUITS ELECTRONIQUES UTILISES
A.3.1 On considère le circuit suivant (cf. figure 3) où l'amplificateur est idéal et fonctionne en régime linéaire. Les tensions
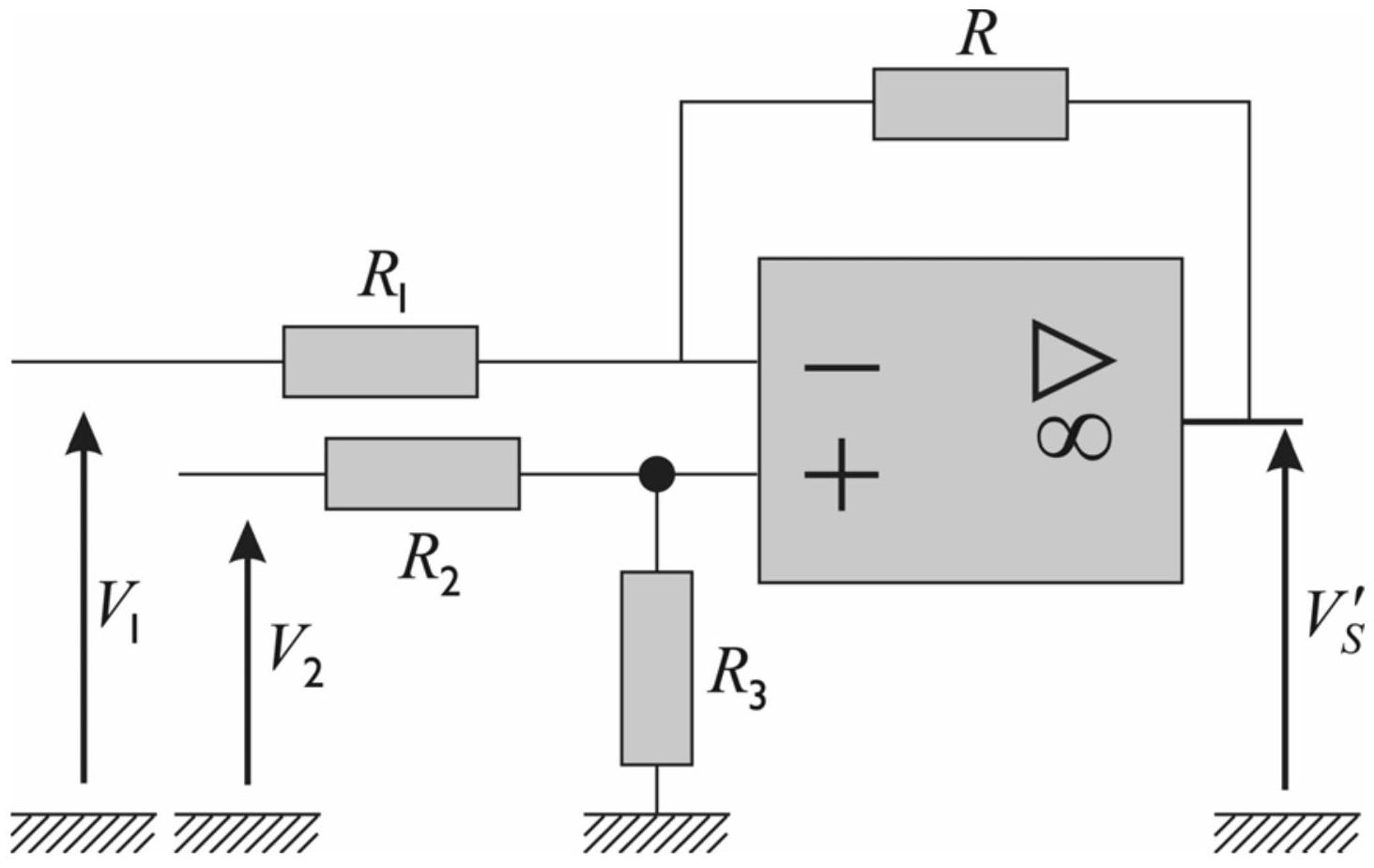
Figure 3 : montage soustracteur
A.3.2 Une photodiode est un composant non linéaire dont la caractéristique courant - tension dépend de l'intensité lumineuse arrivant sur la photodiode (aucune connaissance sur les dipôles non linéaires n'est requise pour traiter cette question). La caractéristique de la photodiode est donnée sur la figure 4 . Dans quelle partie de la caractéristique devrait se situer le point de fonctionnement (
A.3.3 On branche la photodiode en série avec un générateur de Thévenin
A.3.4 Quelle tension peut-on alors injecter à l'une des entrées du soustracteur ?
A.3.3 On branche la photodiode en série avec un générateur de Thévenin
A.3.4 Quelle tension peut-on alors injecter à l'une des entrées du soustracteur ?
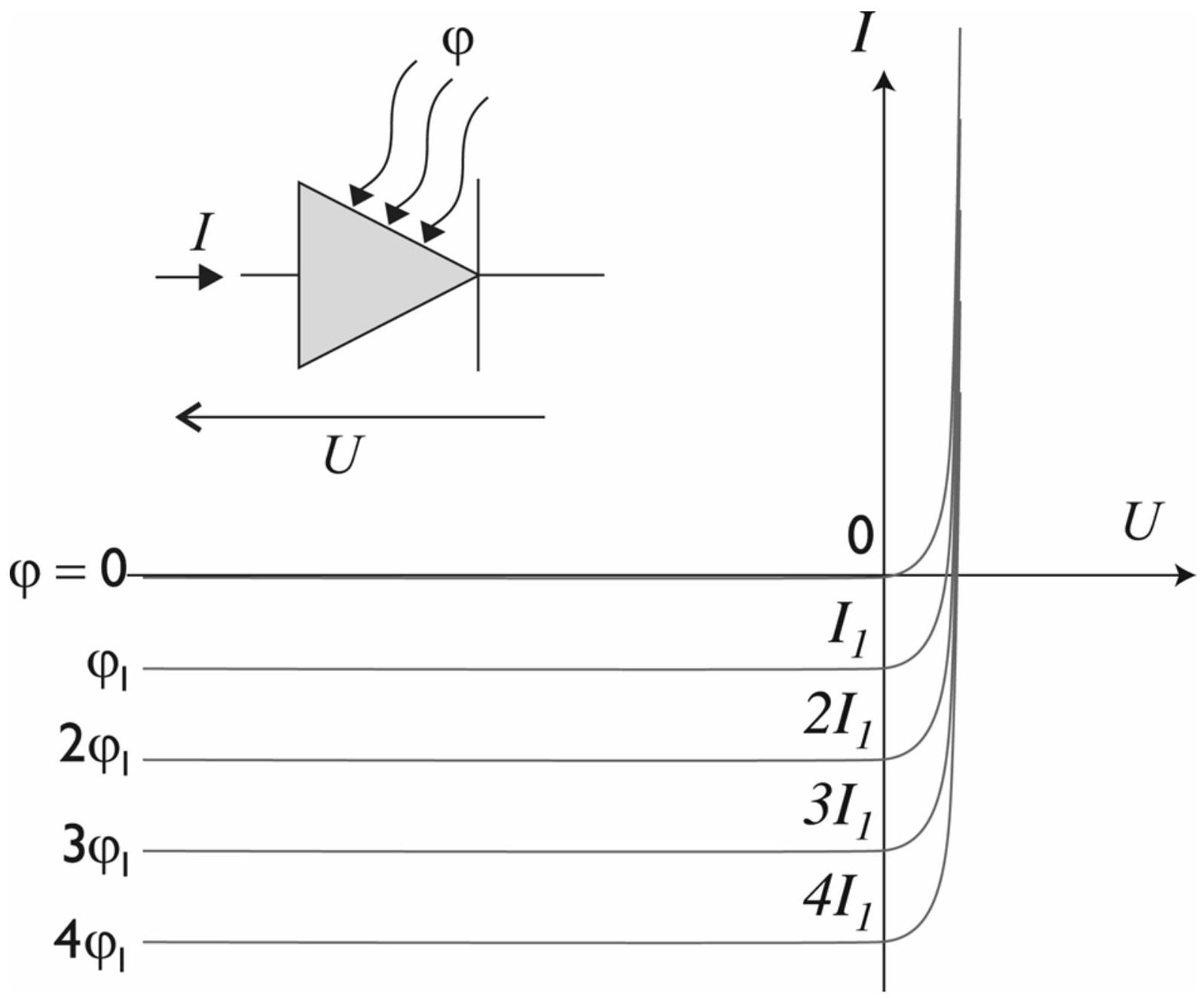
Figure 4 : Caractéristique de la photodiode
FIN DU PREMIER PROBLÈME
PROBLÈME B : VARIATION DE PRESSION DANS UN TUBE INDEFORMABLE
Les questions de ce problème constituent une suite logique et sont donc à traiter dans l'ordre indiqué. Certaines des questions peuvent donner lieu à une application numérique, une attention toute particulière y sera donnée lors de la correction de ce problème.
Dans ce problème, on prendra pour la constante des gaz parfaits
B. 1 PRÉAMBULE
On considère un gaz réel (air) contenu dans un tube indéformable de section interne
B.1.1 Sachant que la densité au repos vaut
B.1.1 Sachant que la densité au repos vaut
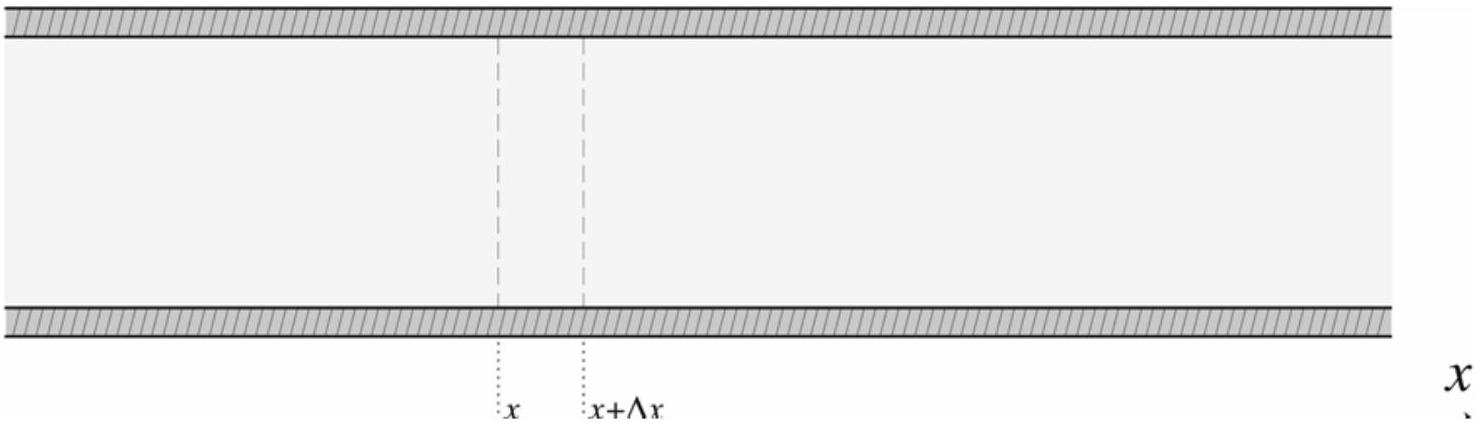
Figure 1: vue en coupe du tube de section interne
B.1.2 Sous l'effet d'une variation de pression
B.1.3 Le volume
B.1.3 Le volume
Dans tout ce problème, on se limitera au premier ordre des développements limités utilisés.
B.1.4 En déduire l'équation qui régit le mouvement
B.1.4 En déduire l'équation qui régit le mouvement
B. 2 EQUATIONS DU MOUVEMENT
Dans un milieu élastique, les variations relatives de volume
B.2.1 Notons
B.2.2 En déduire la relation qui lie la surpression
B.2.3 En utilisant les résultats de B.1.4 et B.2.2, déterminer les équations du mouvement. On écrira cette expression de manière à n'avoir qu'une seule constante.
B.2.4 Reconnaissez-vous cette équation ?
B.2.5 Donner la signification physique de la constante.
B.2.6 Commenter l'influence respective des différents paramètres physiques régissant cette constante. Ces paramètres vous paraissent-ils indépendants ?
B.2.1 Notons
B.2.2 En déduire la relation qui lie la surpression
B.2.3 En utilisant les résultats de B.1.4 et B.2.2, déterminer les équations du mouvement. On écrira cette expression de manière à n'avoir qu'une seule constante.
B.2.4 Reconnaissez-vous cette équation ?
B.2.5 Donner la signification physique de la constante.
B.2.6 Commenter l'influence respective des différents paramètres physiques régissant cette constante. Ces paramètres vous paraissent-ils indépendants ?
B. 3 EVOLUTION DE LA PRESSION
B.3.1 Connaissant les équations régissant les déplacements
B.3.2 Donner et commenter les formes des solutions attendues pour
B.3.3 Par analogie, déduire les équations qui pourraient, dans ce cadre, régir la pression
B.3.2 Donner et commenter les formes des solutions attendues pour
B.3.3 Par analogie, déduire les équations qui pourraient, dans ce cadre, régir la pression
B. 4 EVOLUTION DE LA DENSITE
On s'intéresse maintenant à la densité
B.4.1 En vous souvenant de la définition de la densité
B.4.2 En déduire la relation entre la densité
B.4.3 En déduire l'équation régissant la densité
B.4.1 En vous souvenant de la définition de la densité
B.4.2 En déduire la relation entre la densité
B.4.3 En déduire l'équation régissant la densité
B. 5 VITESSE CARACTERISTIQUE
B.5.1 Considérons maintenant un gaz parfait mono-atomique. En utilisant B.4.2 déterminer la valeur de
B.5.2 On applique ce résultat à différents gaz mono-atomiques dont les masses molaires sont consignées dans le tableau suivant. Compléter le tableau (sur votre copie) et commenter les valeurs obtenues. Vous attendiez-vous à ces valeurs ?
B.5.2 On applique ce résultat à différents gaz mono-atomiques dont les masses molaires sont consignées dans le tableau suivant. Compléter le tableau (sur votre copie) et commenter les valeurs obtenues. Vous attendiez-vous à ces valeurs ?
| élément | He | Ne | Ar | Kr | Xe | |||||
|
|
4,003 | 20,18 | 39,95 | 86,8 | 131,3 |
B.5.3 Dans le cas d'une transformation adiabatique réversible, on peut utiliser la loi de Laplace. Citez-la.
B.5.4 Quelle relation entre la densité et la pression implique-t-elle ?
B.5.5 Quel est le nombre de degrés de liberté
B.5.6 Quels sont les degrés de liberté qui se rajoutent dans le cas d'une molécule diatomique supposé rigide comme l'oxygène (
B.5.7 La constante
B.5.8 En différentiant l'expression de Laplace, déterminer l'expression littérale de
B.5.9 Déterminer la valeur de
B.5.10 Quelle masse intervient dans B.5.9 dans le cas de l'air? On rappelle que l'air est composé d'environ
B.5.11 Dans ces conditions, quelle valeur obtenez-vous dans l'application numérique de B.5.9 ? Est-ce la valeur que vous attendiez ? Commentez.
B.5.4 Quelle relation entre la densité et la pression implique-t-elle ?
B.5.5 Quel est le nombre de degrés de liberté
B.5.6 Quels sont les degrés de liberté qui se rajoutent dans le cas d'une molécule diatomique supposé rigide comme l'oxygène (
B.5.7 La constante
B.5.8 En différentiant l'expression de Laplace, déterminer l'expression littérale de
B.5.9 Déterminer la valeur de
B.5.10 Quelle masse intervient dans B.5.9 dans le cas de l'air? On rappelle que l'air est composé d'environ
B.5.11 Dans ces conditions, quelle valeur obtenez-vous dans l'application numérique de B.5.9 ? Est-ce la valeur que vous attendiez ? Commentez.
B. 6 SOLUTIONS
Maintenant que notre système est formalisé, il nous reste à l'appliquer à une situation concrète. On considère donc un tube de longueur
B.6.1 Donner les solutions physiques pour la pression acoustique
B.6.2 A quoi correspond cette solution?
B.6.3 En déduire la solution donnant
B.6.4 Que vaut la constante d'intégration? Expliquer pourquoi.
B.6.5 Quelle est la relation de phase entre
B.6.6 Faites un petit dessin illustrant la situation.
B.6.7 Commenter les conditions aux limites pour
B.6.1 Donner les solutions physiques pour la pression acoustique
B.6.2 A quoi correspond cette solution?
B.6.3 En déduire la solution donnant
B.6.4 Que vaut la constante d'intégration? Expliquer pourquoi.
B.6.5 Quelle est la relation de phase entre
B.6.6 Faites un petit dessin illustrant la situation.
B.6.7 Commenter les conditions aux limites pour
B. 7 FLUX D'ENERGIE ACOUSTIQUE
On se place maintenant dans un milieu infini où une source sonore de petite taille produit un son sinusoïdal caractérisé par une variation de pression acoustique
B.7.1 Quelle est la principale différence par rapport à la situation B.6 ?
B.7.2 Quelle solution pouvez-vous proposer dans ces conditions pour la pression acoustique ? On introduira l'amplitude crête-à-crête
B.7.3 Quelle relation définit le vecteur d'onde
B.7.4 Donner l'expression du déplacement
B.7.5 On s'intéresse à la densité de flux d'énergie acoustique
B.7.6 L'intensité acoustique
B.7.7 Le seuil d'audition d'une oreille humaine correspond à une intensité de
B.7.8 Quelle est l'amplitude crête-à-crête
B.7.1 Quelle est la principale différence par rapport à la situation B.6 ?
B.7.2 Quelle solution pouvez-vous proposer dans ces conditions pour la pression acoustique ? On introduira l'amplitude crête-à-crête
B.7.3 Quelle relation définit le vecteur d'onde
B.7.4 Donner l'expression du déplacement
B.7.5 On s'intéresse à la densité de flux d'énergie acoustique
B.7.6 L'intensité acoustique
B.7.7 Le seuil d'audition d'une oreille humaine correspond à une intensité de
B.7.8 Quelle est l'amplitude crête-à-crête
B. 8 INTENSITE ACOUSTIQUE
La sensation auditive étant, d'après la loi de Fechner, proportionnelle au Log (décimal) de l'excitation, cette dernière est exprimée dans l'unité appropriée, le décibel :
où
B.8.1 Laquelle des deux expressions convient à la définition de l'intensité acoustique en fonction de la surpression
B.8.2 La pression de référence ( 0 dB ) correspond à 2 dixmillièmes de millibar. Quelle est la valeur correspondante en unité SI et quelle est l'unité appropriée ?
B.8.3 En prenant cette valeur pour la surpression crête-à-crête
B.8.4 Un train passant en gare à pleine vitesse produirait sur le quai un son dont l'intensité peut atteindre les 120 dB à une fréquence de l'ordre de 100 Hz . Quel est le rapport entre l'amplitude crête-à-crête générée par le train
B.8.5 Comparer ce déplacement à celui lié au seuil d'audition. Commentez.
B.8.1 Laquelle des deux expressions convient à la définition de l'intensité acoustique en fonction de la surpression
B.8.2 La pression de référence ( 0 dB ) correspond à 2 dixmillièmes de millibar. Quelle est la valeur correspondante en unité SI et quelle est l'unité appropriée ?
B.8.3 En prenant cette valeur pour la surpression crête-à-crête
B.8.4 Un train passant en gare à pleine vitesse produirait sur le quai un son dont l'intensité peut atteindre les 120 dB à une fréquence de l'ordre de 100 Hz . Quel est le rapport entre l'amplitude crête-à-crête générée par le train
B.8.5 Comparer ce déplacement à celui lié au seuil d'audition. Commentez.
FIN DU PROBLÈME B
FIN DE L'ENONCE.
