La théorie cinétique des gaz vise à expliquer le comportement macroscopique d'un gaz à partir des mouvements des particules qui le composent. Depuis la naissance de l'informatique, de nombreuses simulations numériques ont permis de retrouver les lois de comportement de différents modèles de gaz comme celui du gaz parfait.
Ce sujet s'intéresse à un gaz parfait monoatomique. Nous considérerons que le gaz étudié est constitué de

particules sphériques, toutes identiques, de masse

et de rayon

, confinées dans un récipient rigide. Les simulations seront réalisées dans un espace à une, deux ou trois dimensions ; le récipient contenant le gaz sera, suivant le cas, un segment de longueur

, un carré de côté

ou un cube d'arête

.
Dans le modèle du gaz parfait, les particules ne subissent aucune force (leur poids est négligé) ni aucune autre action à distance. Elle n'interagissent que par l'intermédiaire de chocs, avec une autre particule ou avec la paroi du récipient. Ces chocs sont toujours élastiques, c'est-à-dire que l'énergie cinétique totale est conservée.
Les seuls langages de programmation autorisés dans cette épreuve sont Python et SQL. Pour répondre à une question il est possible de faire appel aux fonctions définies dans les questions précédentes. Dans tout le sujet on suppose que les bibliothèques math, numpy et random ont été importées grâce aux instructions

import math
import numpy as np
import random

Si les candidats font appel à des fonctions d'autres bibliothèques ils doivent préciser les instructions d'importation correspondantes.
Ce sujet utilise la syntaxe des annotations pour préciser le types des arguments et du résultat des fonctions à écrire. Ainsi

def maFonction(n:int, x:float, l:[str]) -> (int, np.ndarray):

signifie que la fonction maFonction prend trois arguments, le premier est un entier, le deuxième un nombre à virgule flottante et le troisième une liste de chaines de caractères et qu'elle renvoie un couple dont le premier élément est un entier et le deuxième un tableau numpy. Il n'est pas demandé aux candidats de recopier les entêtes avec annotations telles qu'elles sont fournies dans ce sujet, ils peuvent utiliser des entêtes classiques. Ils veilleront cependant à décrire précisément le rôle des fonctions qu'ils définiraient eux-mêmes.
Une liste de fonctions utiles est donnée à la fin du sujet.

Représentation en Python

Chaque particule est représentée par une liste de deux éléments, le premier correspond à la position de son centre, la deuxième à sa vitesse. Chacun de ces éléments (position et vitesse) est représenté par un vecteur (np.ndarray) dont le nombre de composantes correspond à la dimension de l'espace de simulation.
Les positions et vitesses sont exprimées sous forme de coordonnées cartésiennes dans un repère orthonormé dont l'origine est placée dans un coin du récipient contenant le gaz et dont les axes sont parallèles aux côtés du récipient issus de ce coin de façon à ce que tout point situé à l'intérieur du récipient ait ses coordonnées comprises entre 0 et

.
Les positions sont exprimées en mètres et les vitesses en

. La figure 1 propose des exemples de particules dans des espaces de diverses dimensions.

p1 = [np.array([5.3]), np.array([412.3])] # 1D
p2 = [np.array([3.1, 4.8]), np.array([241, -91.4])] # 2D
p3 = [np.array([5.2, 3.2, 2.3]), np.array([-130.1, 320, 260.2])] # 3D

Figure 1 Exemples de particules

I Initialisation

Pour pouvoir réaliser une simulation, il convient de disposer d'une situation initiale, c'est-à-dire d'un ensemble de particules réparties dans le récipient et dotées d'une vitesse initiale connue. Cette partie s'intéresse au positionnement aléatoire d'un ensemble de particules. L'attribution de vitesses initiales à ces particules ne sera pas abordé ici.

I.A - Placement en dimension 1

Nous cherchons d'abord comment placer

particules (sphères de rayon

) le long d'un segment de longueur

sans qu'elles se chevauchent ni qu'elles sortent du segment. La figure 2 montre quelques exemples de placements possibles avec

Figure 2 Exemples de placement de 5 particules de rayon 0,5 sur un segment de longueur 10

La fonction placement1D construit aléatoirement, à partir des paramètres géométriques du problème (nombre et rayon des particules, taille du récipient), une liste de coordonnées correspondant à la position initiale du centre de chaque particule.

def placement1D(N:int, R:float, L:float) -> [np.ndarray]:
    def possible(c:np.ndarray) -> bool:
        if c[0] < R or c[0] > L - R: return False
        for p in res:
            if abs(c[0] - p[0]) < 2*R: return False
        return True
    res = []
    while len(res) < N:
        p = L * np.random.rand(1)
        if possible(p): res.append(p)
    return res

Q 1. Détailler l'action de la ligne 9.
Q 2. Quelle est la signification du paramètre c de la fonction possible (ligne 2) ?
Q 3. Expliquer le rôle de la ligne 3.
Q 4. Expliquer le rôle des lignes 4 et 5.
Q 5. Donner en une phrase le rôle de la fonction possible.
Q 6. Proposer une nouvelle version de la ligne 9 permettant d'éviter certains rejets de la part de la fonction possible.
Q 7. On considère l'appel placement1D(4,

) et on suppose que les trois premières particules ont été placées aux points d'abscisses

et 4 (figure 3). Quelle sera la suite du déroulement de la fonction placement1D?

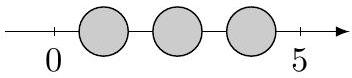
Figure 3

Q 8. Quelle est la complexité temporelle de la fonction placement1D dans le cas où

, nombre maximal de particules de rayon

pouvant être placées sur un segment de longueur

?
Q 9. Pour remédier de manière simple (mais non optimale) à la situation de la question 7 , on décide de recommencer à zéro le placement des particules dès qu'une particule est rejetée par la fonction possible. Réécrire les lignes 7 à 11 de la fonction placement1D pour mettre en œuvre cette décision.

I.B - Optimisation du placement en dimension 1

Pour placer aléatoirement

particules le long d'un segment, nous envisageons une approche plus efficace que celle étudiée dans la sous-partie I.A.
L'idée est de calculer l'espace laissé libre sur le segment cible par

particules puis de répartir aléatoirement cet espace libre entre les particules. Afin de conserver une répartition uniforme des particules dans tout le segment, nous utilisons l'algorithme suivant:

déterminer , espace laissé libre par les particules dans le segment ;
placer aléatoirement dans le segment particules virtuelles ponctuelles ; à cette étape, deux particules peuvent parfaitement occuper la même abscisse : il n'y a pas de conflit ;
remplacer chaque particule virtuelle par une particule réelle de rayon en décalant toutes les particules (réelles et virtuelles) situées plus à droite de façon à dégager l'espace nécessaire.
Q 10. Écrire la fonction d'entête
def placement1Drapide(N:int, R:float, L:float) -> [np.ndarray]:
qui implante cet algorithme et renvoie la liste des coordonnées des centres de particules de rayon réparties aléatoirement le long d'un segment situé entre les abscisses 0 et L . On précise que l'ordre de la liste résultat n'est pas important.
Q 11. Quelle est la complexité de la fonction placement1Drapide ? Commenter.

I.C - Analyse statistique

Afin de vérifier que la fonction placement1Drapide produit une répartition de particules uniformément répartie sur le segment cible, on l'appelle un grand nombre de fois et on comptabilise pour chaque résultat obtenu la position initiale de chaque particule. Le résultat final est présenté sous forme d'un histogramme dont l'axe horizontal correspond à l'abscisse du centre de la particule dans l'intervalle

et l'axe vertical au nombre total de particules placées à cette abscisse au cours des différentes exécutions de la fonction.
Q 12. Tracer et justifier l'allure des histogrammes pour

dans le cas où

I.D - Dimension quelconque

L'algorithme optimisé pour un segment, n'est pas utilisable pour des espaces de dimensions supérieures. Nous allons donc généraliser la fonction placement1D pour la transformer en une fonction utilisable dans un espace de dimension 1,2 ou 3 .
Q 13. En s'inspirant de la fonction placement1D, écrire la fonction d'entête
def placement(D:int, N:int, R:float, L:float) -> [np.ndarray]:
qui renvoie la liste des coordonnées des centres de

particules sphériques de rayon

placées aléatoirement dans un récipient de côté L dans un espace à D dimensions. Les modifications prévues aux questions 6 et 9 seront prises en compte dans cette fonction.

II Mouvement des particules

On suppose que l'on dispose désormais d'une fonction d'entête
def situationInitiale(D:int, N:int, R:float, L:float) -> [[np.ndarray, np.ndarray]]:
qui renvoie une liste de

particules de rayon

, représentées chacune par une liste à deux éléments (position et vitesse, cf. figure 1), placées aléatoirement à l'intérieur d'un récipient de taille

dans un espace à

dimensions. À partir de cette situation initiale, les positions et vitesses des particules vont évoluer au gré du déplacement des particules, des différents chocs entre elles et des rebonds sur les parois. On appelle évènement chaque choc ou rebond.

II.A - Analyse physique

Q 14. Comment évolue une particule entre deux évènements ?
Plaçons-nous dans un espace à une dimension et considérons deux particules de masses

qui entrent en collision avec les vitesses initiales

. Les vitesses

des deux particules après le choc sont données par

Q 15. Que deviennent ces formules lorsque

? Commenter.
Q 16. Que deviennent ces formules lorsque

? À quelle situation ce cas correspond-t-il dans le problème qui nous occupe ?

II.B - Évolution des particules

Q 17. Écrire la fonction d'entête
def vol ( p : [np.ndarray, np.ndarray],

float)

None:
qui met à jour l'état de la particule p (position et vitesse dans un espace de dimension quelconque) au bout d'un vol de

secondes sans choc ni rebond.
Q 18. Écrire la fonction d'entête
def rebond(p:[np.ndarray, np.ndarray], d:int) -> None:
qui met à jour la vitesse de la particule

suite à un rebond sur une paroi perpendiculaire à la dimension d'indice d, c'est-à-dire l'axe des abscisses si d vaut 0 , l'axe des ordonnées si d vaut 1 et l'axe des cotes si d vaut 2 .
Par généralisation du résultat obtenu dans un espace à une dimension, on supposera que le rebond d'une particule sur une paroi ne modifie pas la composante de la vitesse parallèle à la paroi et change le signe de sa composante normale à la paroi (rebond parfait). La fonction rebond n'est pas chargée de vérifier que la particule se trouve au contact d'une paroi.
Q 19. On revient dans un espace à une dimension. Écrire la fonction d'entête def choc(p1:[np.ndarray, np.ndarray], p2:[np.ndarray, np.ndarray]) -> None:
qui modifie les vitesses des deux particules, p1 et p2, suite au choc de l'une contre l'autre. La fonction choc n'est pas chargée de vérifier que les deux particules sont en contact.
On supposera dans la toute la suite que l'on dispose d'une version de la fonction choc également opérationnelle dans un espace à deux et trois dimensions.

III Inventaire des évènements

Chaque évènement sera représenté par une liste de cinq éléments avec la signification suivante :
0 . un booléen indiquant si l'évènement est valide ou pas ;

un flottant donnant le nombre de secondes, à partir de l'instant courant, au bout duquel l'évènement aura lieu;
un entier compris entre 0 et donnant l'indice dans la liste des particules de la première (ou seule) particule concernée par l'évènement;
un entier compris entre 0 et donnant l'indice de la deuxième particule concernée par l'évènement ou None s'il n'y a pas de deuxième particule concernée (l'évènement est un rebond sur une paroi) ;
un entier compris entre 0 et donnant l'indice de la dimension perpendiculaire à la paroi concernée par l'évènement ou None s'il n'y a pas de paroi concernée (l'évènement est un choc entre deux particules).
On supposera, sans avoir besoin de le vérifier, qu'on a toujours une et une seule valeur None parmi les deux derniers éléments de tout évènement.
Ainsi [True, 0.4, 34, 57, None] désigne le choc entre les particules d'indice 34 et 57 qui aura lieu dans . Et [True, 1.7, 34, None, 1] désigne le rebond de la particule d'indice 34 sur une paroi perpendiculaire à la dimension d'indice 1 (axe des ordonnées) qui aura lieu dans .

III.A - Prochains évènements dans un espace à une dimension

Q 20. Écrire, pour un espace à une dimension, la fonction d'entête
def

. ndarray, np.ndarray], R:float, L:float) -> None or (float, int):
qui détermine dans combien de temps la particule p , de rayon

, rencontrera une paroi du récipient de taille

, en faisant abstraction de toute autre particule qui pourrait se trouver sur son chemin. Cette fonction renvoie None si la particule ne rencontre jamais de paroi, sinon elle renvoie un couple dont le premier élément est la durée (en secondes) avant le rebond et le deuxième la direction de la paroi désignée par l'indice de sa dimension perpendiculaire.
Q 21. Toujours dans un espace à une dimension, écrire la fonction d'entête
def tc(p1:[np.ndarray, np.ndarray], p2:[np.ndarray, np.ndarray], R:float) -> None or float: qui détermine si les deux particules p1 et p2, de rayon

, vont se rencontrer, en faisant abstraction de la présence des autres particules et des parois, autrement dit en considérant que ces deux particules sont seules dans un espace infini. Cette fonction renvoie None si les deux particules ne se rencontrent jamais, sinon elle renvoie le temps (en secondes) au bout duquel les particules entrent en collision.
On supposera dans la toute la suite que l'on dispose d'une version des fonction tr et tc également opérationnelles dans un espace à deux et trois dimensions.

III.B - Catalogue d'évènements

Afin d'alimenter l'algorithme de la partie suivante, on souhaite construire un catalogue des évènements qui pourraient se produire prochainement. Ce catalogue sera représenté par une liste dans laquelle les évènements, représentés par la liste de cinq éléments décrite au début de cette partie, sont ordonnés par date décroissante : le plus lointain en début de liste, le plus proche en fin de liste.
Q 22. Écrire la fonction d'entête
def ajoutEv(catalogue:[[bool, float, int, int or None, int or None]], e: [bool, float, int, int or None, int or None]) -> None:
qui ajoute au bon endroit dans la liste catalogue l'évènement e. La liste catalogue contient des évènements ordonnés par temps décroissant.
Q 23. Écrire la fonction d'entête
def ajout1p(catalogue:[[bool, float, int, int or None, int or None]], i:int,
R:float, L:float, particules:[[np.ndarray, np.ndarray]]) -> None:
qui ajoute, dans la liste ordonnée d'évènements catalogue, les prochains évènements potentiels concernant la particule d'indice i de la liste particules qui contient toutes les particules présentes dans le récipient. Le paramètre R donne le rayon d'une particule et L la taille du récipient. Les évènements à prendre en compte sont le prochain rebond contre une paroi et le prochain choc avec chacune des autres particules (cf III.A). Les prochains évènements seront supposés valides et la fonction veillera à maintenir ordonnée la liste catalogue.
Q 24. Écrire la fonction d'entête
def initCat(particules:[[np.ndarray, np.ndarray]], R:float,
L:float) -> [[bool, float, int, int or None, int or None]]:
qui utilise la fonction ajout1p et qui renvoie la liste, ordonnée par temps décroissant, des prochains évènements potentiels concernant une liste de particules particules de rayon

dans un récipient de taille

.
Q 25. Expliquer pourquoi la liste renvoyée par la fonction initCat contient certains éléments qui correspondent en fait au même évènement.
Q 26. Déterminer la complexité temporelle de la fonction initCat pour un espace à une dimension.
Q 27. Quelle est la fonction à optimiser en priorité afin d'améliorer la complexité de la fonction initCat ? Quel algorithme classique peut être utilisé pour optimiser cette fonction?

IV Simulation

Nous disposons désormais des éléments de base pour simuler l'évolution d'un ensemble de particules identiques enfermées dans un récipient. En partant d'une situation initiale, nous pouvons déterminer les prochains évènements possibles, le plus proche de ces évènements va forcément avoir lieu. Nous pouvons alors établir un nouvel état de l'ensemble des particules juste après cet évènement, puis déterminer une nouvelle liste des prochains évènements possibles à partir de cette nouvelle situation. En répétant ce traitement, il est théoriquement possible de déterminer la position et la vitesse de chacune des particules à un instant quelconque dans le futur.
Q 28. Montrer que la liste des prochains évènements possibles ne peut jamais être vide, sauf si toutes les particules sont initialement à l'arrêt.
Dans toute la suite, nous considèrerons qu'au moins une particule est en mouvement.
Q 29. Écrire la fonction d'entête
def etape(particules:[[np.ndarray, np.ndarray]],
e: [bool, float, int, int or None, int or None]) -> None:
qui, partant d'une liste de particules particules représentant la situation à l'instant courant, modifie l'état de chaque particule pour refléter la situation des particules juste après l'évènement e (supposé valide), en supposant qu'aucun autre évènement n'arrive avant celui-ci.
Disposant de la fonction etape, il suffirait de la combiner avec la fonction initCat pour implanter l'algorithme de simulation décrit plus haut. Cependant, étant donné la complexité de initCat, il semble intéressant d'optimiser cette phase de l'algorithme. Pour cela, remarquons que les évènements qui ne concernent par les particules impliquées dans l'évènement traité par la fonction etape restent valides, à un décalage temporel près. Les seuls nouveaux prochains évènements possibles concernent les particules impliquées dans l'évènement traité.
Q 30. Écrire la fonction d'entête
def majCat(catalogue:[[bool, float, int, int or None, int or None]],
particules: [[np.ndarray, np.ndarray]],
e:[bool, float, int, int or None, int or None], R:float, L:float) -> None:
qui met à jour son paramètre catalogue, liste ordonnée des prochains évènements potentiels, en supposant que particules représente la situation juste après l'évènement e, supposé valide et déjà retiré de catalogue. Les paramètres R et

désignent respectivement le rayon d'une particule et la taille du récipient. Afin de limiter les
manipulations de listes, les évènements qui n'ont plus cours seront conservés dans le catalogue et simplement marqués non valides.
On dispose de la fonction d'entête

def enregistrer(bdd, t:float, e:[bool, float, int, int or None, int or None],
    particules:[[np.ndarray, np.ndarray]]) -> None:

qui enregistre dans la base de données bdd des informations à propos de l'évènement e survenu au temps t de la simulation. Le temps de la simulation est exprimé en secondes, le début de la simulation étant pris comme origine. Le paramètre particules donne la situation (position, vitesse) des particules au temps t considéré, juste après la survenue de l'évènement

.
Q 31. Écrire la fonction d'entête
def simulation(bdd, d:int, N:int, R:float, L:float, T:float) -> int:
qui simule l'évolution de

particules identiques de rayon

dans un récipient de côté

dans un espace à

dimensions pendant la durée T (exprimée en secondes). Cette fonction utilise une situation initiale générée aléatoirement par l'intermédiaire de la fonction situationInitiale (partie II) et renvoie le nombre d'évènements ayant eu lieu pendant toute la simulation. D'autre part, elle enregistre chaque évènement dans la base de données bdd.
Q 32. Comment sont gérés les doublons repérés à la question 25 ?
Q 33. Dans la représentation choisie pour les évènements, le temps auquel cet évènement peut survenir est donné par rapport à un instant courant (qui correspond à l'instant de l'évènement précédent dans l'implantation choisie) ce qui oblige à recaler chaque évènement au fur et à mesure que le temps de la simulation s'écoule. Une autre possibilité aurait été d'indiquer le temps de chaque évènement par rapport à une référence fixe (le début de la simulation). Discuter des avantages et des inconvénients de chaque représentation en terme de précision du résultat et de complexité de l'algorithme. La représentation retenue ici est-elle la mieux adaptée des deux pour traiter le problème posé ?

V Exploitation des résultats

On dispose d'une version plus générale de la fonction simulation pour laquelle toutes les particules ne sont plus nécessairement identiques. Cette fonction enregistre ses résultats dans une base de données dont la structure est donnée figure 4.

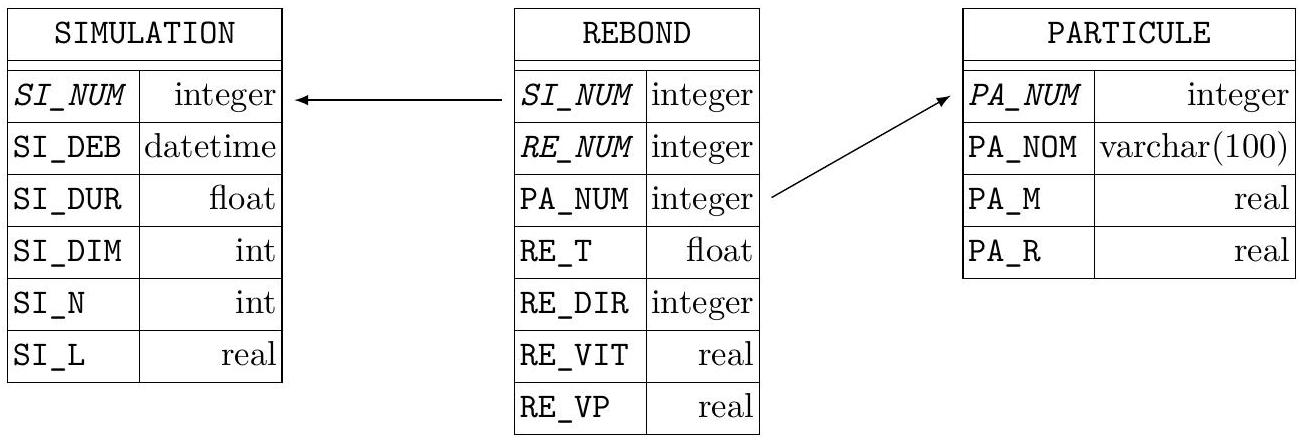
Figure 4 Structure physique de la base de données des résultats de simulation

Cette base comporte les trois tables suivantes:

la table SIMULATION, de clef primaire SI_NUM, donne les caractéristiques de chaque simulation effectuée. Elle contient les colonnes
SI_NUM numéro d'ordre de la simulation (clef primaire)
SI_DEB date et heure du lancement du programme de simulation
SI_DUR durée (en secondes) de la simulation (il ne s'agit pas du temps d'exécution du programme, mais du temps simulé)
SI_DIM nombre de dimensions de l'espace de simulation
SI_N nombre de particules pour cette simulation
SI_L (en mètres) taille du récipient utilisé pour la simulation
la table PARTICULE, de clef primaire PA_NUM, des types de particules considérées. Elle contient les colonnes
PA_NUM numéro (entier) identifiant le type de particule (clef primaire)
PA_NOM nom de ce type de particule
PA_M masse de la particule (en grammes)
PA_R rayon (en mètres) de la particule
la table REBOND, de clef primaire (SI_NUM, RE_NUM), liste les chocs des particules avec les parois du récipient. Elle contient les colonnes
SI_NUM numéro d'ordre de la simulation ayant généré ce rebond
RE_NUM numéro d'ordre du rebond au sein de cette simulation
PA_NUM numéro du type de particule concernée par ce rebond
RE_T temps de simulation (en secondes) auquel ce rebond est arrivé
RE_DIR paroi concernée : entier non nul de l'intervalle [-SI_DIM, SI_DIM] donnant la direction de la normale à la paroi. Ainsi -2 désigne la paroi située en alors que 1 désigne la paroi située en
RE_VIT norme de la vitesse de la particule qui rebondit (en )
RE_VP valeur absolue de la composante de la vitesse normale à la paroi (en )

Q 34. Écrire une requête SQL qui donne le nombre de simulations effectuées pour chaque nombre de dimensions de l'espace de simulation.
Q 35. Écrire une requête SQL qui donne, pour chaque simulation, le nombre de rebonds enregistrés et la vitesse moyenne des particules qui frappent une paroi.
Q 36. Écrire une requête SQL qui, pour une simulation

donnée, calcule, pour chaque paroi, la variation de quantité de mouvement due aux chocs des particules sur cette paroi tout au long de la simulation. On se rappellera que lors du rebond d'une particule sur une paroi la composante de sa vitesse normale à la paroi est inversée, ce qui correspond à une variation de quantité de mouvement de

où

désigne la masse de la particule et

la composante de sa vitesse normale à la paroi.

Opérations et fonctions Python disponibles

Fonctions

range(n) renvoie la séquence des n premiers entiers ( )
list (range(n)) renvoie une liste contenant les n premiers entiers dans l'ordre croissant:
list(range(5))
random. randrange(a, b) renvoie un entier aléatoire compris entre et inclus (a et entiers)
random. random() renvoie un nombre flottant tiré aléatoirement dans [ 0,1 [ suivant une distribution uniforme
random.shuffle(u) permute aléatoirement les éléments de la liste u (modifie u)
random.sample(u, n) renvoie une liste de n éléments distincts de la liste u choisis aléatoirement, si len(u), déclenche l'exception ValueError
math.sqrt(x) calcule la racine carrée du nombre
math.ceil(x) renvoie le plus petit entier supérieur ou égal à
math.floor(x) renvoie le plus grand entier inférieur ou égal à
sorted(u) renvoie une nouvelle liste contenant les éléments de la liste u triés dans l'ordre « naturel » de ses éléments (si les éléments de u sont des listes ou des tuples, l'ordre utilisé est l'ordre lexicographique)

Opérations sur les listes

len(u) donne le nombre d'éléments de la liste u:
construit une liste constituée de la concaténation des listes et :
construit une liste constitué de la liste u concaténée n fois avec elle-même:
e in u et e not in u déterminent si l'objet e figure dans la liste u

2 in

True ; 2 not in [

]

False

u.append(e) ajoute l'élément e à la fin de la liste (similaire à )
u.pop() renvoie le dernier élément de la liste u (u[-1]) et le supprime (del u[-1])
del u[i] supprime de la liste u son élément d'indice i
del supprime de la liste tous ses éléments dont les indices sont compris dans l'intervalle [i,j[
u.remove(e) supprime de la liste u le premier élément qui a pour valeur e, déclenche l'exception ValueError si e ne figure pas dans u
u.insert (i, e) insère l'élément e à la position d'indice i dans la liste u (en décalant les éléments suivants) ; si i len (u), e est ajouté en fin de liste
— permute les éléments d'indice i et j dans la liste u
u.sort() trie la liste u en place, dans l'ordre «naturel» de ses éléments (si les éléments de u sont des listes ou des tuples, l'ordre utilisé est l'ordre lexicographique)

Opérations sur les tableaux (np.ndarray)

np.array(u) crée un nouveau tableau contenant les éléments de la liste u. La taille et le type des éléments de ce tableau sont déduits du contenu de u
np.empty(n, dtype), np.empty((n, m), dtype) crée respectivement un vecteur à n éléments ou une matrice à n lignes et m colonnes dont les éléments, de valeurs indéterminées, sont de type dtype qui peut être un type standard (bool, int, float, ...) ou un type spécifique numpy (np.int16, np.float32, ...). Si le paramètres dtype n'est pas précisé, les éléments seront de type float
np.zeros(n, dtype), np.zeros((n, m), dtype) fonctionne comme np.empty en initialisant chaque élément à la valeur zéro pour les types numériques ou False pour les types booléens
np.random.rand(n), np.random.rand(n, m) crée un tableau de la forme indiquée (n lignes, m colonnes) en initialisant chaque élément avec une valeur aléatoire issue d'une distribution uniforme sur
a.ndim nombre de dimensions du tableau a (1 pour un vecteur, 2 pour une matrice, etc.)
a.shape tuple donnant la taille du tableau a pour chacune de ses dimensions
len(a) taille du tableau a dans sa première dimension (nombre d'éléments d'un vecteur, nombre de lignes d'une matrice, etc.) équivalent à a.shape[0]
a.size nombre total d'éléments du tableau a
a.flat itérateur sur tous les éléments du tableau a
a.min(), a.max() renvoie la valeur du plus petit (respectivement plus grand) élément du tableau a; ces opérations ont une complexité temporelle en (a.size)
b in a détermine si b est un élément du tableau a ; si b est un scalaire, vérifie si b est un élément de a ; si b est un vecteur ou une liste et a une matrice, détermine si b est une ligne de a
np.concatenate((a1, a2)) construit un nouveau tableau en concaténant deux tableaux ; a1 et a2 doivent avoir le même nombre de dimensions et la même taille à l'exception de leur taille dans la première dimension (deux matrices doivent avoir le même nombre de colonnes pour pouvoir être concaténées)
a.sort(d) trie le tableau a en place suivant sa dimension d'indice (par défaut, la dernière du tableau): a.sort(0) trie les éléments du vecteur a ou les lignes de la matrice a; a.sort(1) trie les colonnes de la matrice a
np.sort(a,d) renvoie une copie triée du tableau a suivant sa dimension d'indice d (voir a.sort(d) pour la signification exacte du paramètre d)