Version interactive avec LaTeX compilé
Le jeu de go
I Introduction au jeu de go
I.A - Présentation du sujet
Ce sujet s'intéresse au jeu de go et à différentes facettes de la construction d'un programme jouant au jeu. La partie 1 présente des règles simplifiées du jeu de go qui seront utilisées tout au long de ce sujet, et qui seront particulièrement utiles aux parties 2 et 5 . Plusieurs fonctions permettant de mener une partie de go seront à implémenter en langage
I.B - Présentation et règles du jeu de go
Le jeu de
Les deux joueurs sont nommés d'après la couleur des pierres qu'ils placent sur le goban : Noir, qui joue en premier et place des pierres noires, et Blanc qui place des pierres blanches. À chaque tour, un joueur place une pierre de sa couleur sur une intersection libre du goban, c'est-à-dire sans pierre. Un coup correspond donc simplement à l'ajout d'une pierre sur une intersection libre, les joueurs ne peuvent pas déplacer une pierre déjà posée.
Nous appellerons configuration du goban, ou simplement goban, l'état du plateau à un moment de la partie, c'est-à-dire la donnée des positions et couleurs de toutes les pierres placées sur le goban. La figure 1 illustre différentes configurations progressives au cours d'une partie possible de go.
Les deux joueurs sont nommés d'après la couleur des pierres qu'ils placent sur le goban : Noir, qui joue en premier et place des pierres noires, et Blanc qui place des pierres blanches. À chaque tour, un joueur place une pierre de sa couleur sur une intersection libre du goban, c'est-à-dire sans pierre. Un coup correspond donc simplement à l'ajout d'une pierre sur une intersection libre, les joueurs ne peuvent pas déplacer une pierre déjà posée.
Nous appellerons configuration du goban, ou simplement goban, l'état du plateau à un moment de la partie, c'est-à-dire la donnée des positions et couleurs de toutes les pierres placées sur le goban. La figure 1 illustre différentes configurations progressives au cours d'une partie possible de go.
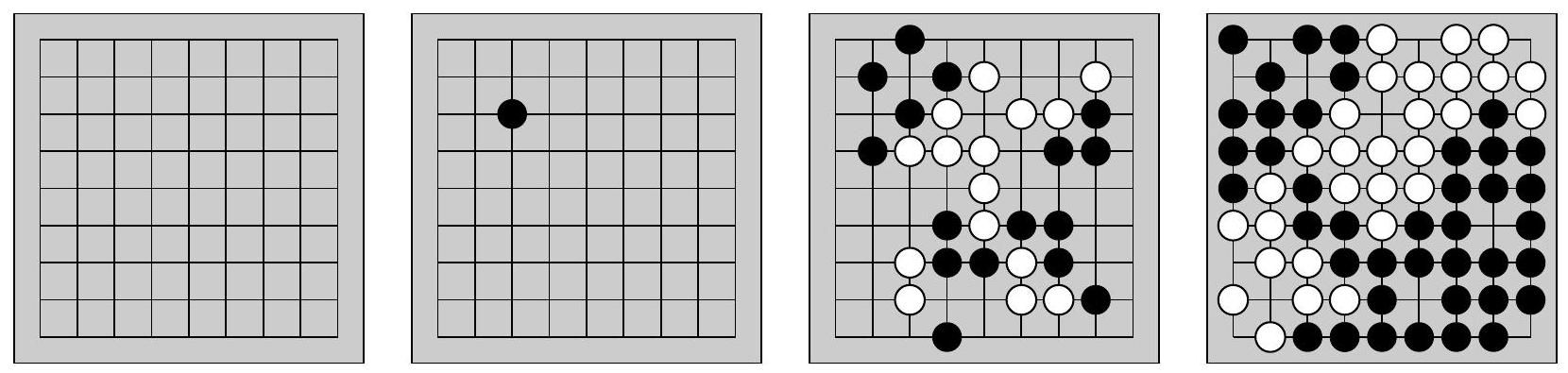
Figure 1 Un goban vide de dimension 9, un premier coup de Noir, une configuration du jeu à un moment intermédiaire, et une configuration à la fin de la partie dans laquelle chaque intersection est contrôlée par un des deux joueurs.
Chaque intersection possède plusieurs intersections voisines qui sont les intersections orthogonalement adjacentes à cette dernière (et non diagonalement adjacentes). Une intersection a donc au plus 4 intersections voisines, celles sur les extrémités du goban pouvant en avoir moins. Par extension, les intersections voisines d'une pierre sont celles de l'intersection où elle est placée.
Deux pierres d'une même couleur sont dites connectées si elles se trouvent sur des intersections voisines. Nous appellerons groupe de pierres une composante connexe pour cette relation de connexion. Chaque groupe possède un nombre de libertés qui est défini comme le nombre d'intersections libres qui sont voisines d'une pierre du groupe. Une intersection voisine de plusieurs pierres du groupe n'est comptée qu'une seule fois.
Un groupe de pierres auquel on vient de supprimer la dernière liberté est capturé, et les pierres de ce groupe sont alors immédiatement retirées du plateau. Ces notions de libertés et de capture sont illustrées dans la figure 2.
Deux pierres d'une même couleur sont dites connectées si elles se trouvent sur des intersections voisines. Nous appellerons groupe de pierres une composante connexe pour cette relation de connexion. Chaque groupe possède un nombre de libertés qui est défini comme le nombre d'intersections libres qui sont voisines d'une pierre du groupe. Une intersection voisine de plusieurs pierres du groupe n'est comptée qu'une seule fois.
Un groupe de pierres auquel on vient de supprimer la dernière liberté est capturé, et les pierres de ce groupe sont alors immédiatement retirées du plateau. Ces notions de libertés et de capture sont illustrées dans la figure 2.
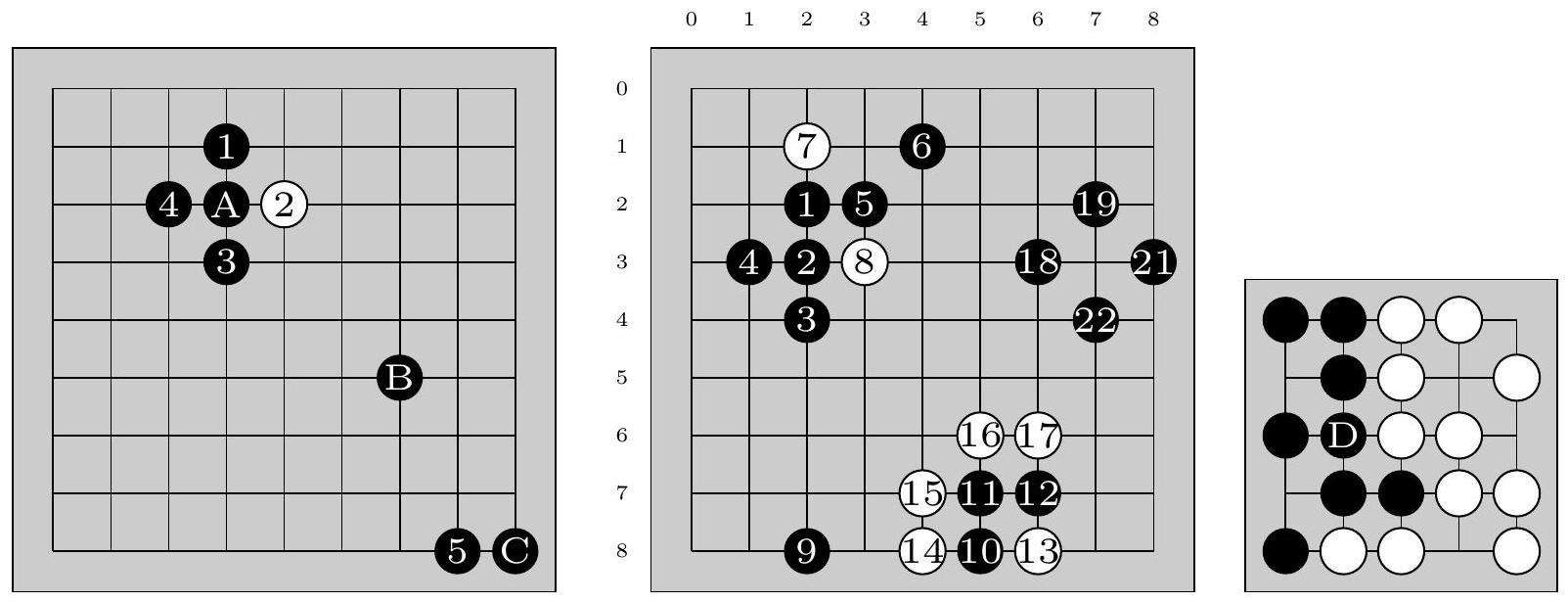
Figure 2 À gauche: la pierre A a une pierre sur chacune de ses 4 intersections voisines. La pierre B n'a pas de pierres sur ses 4 intersections voisines. La pierre C a une pierre sur une de ses deux intersections voisines. Au milieu : les pierres 1,2,3,4 et 5 forment un groupe de pierres noires, la pierre 6 ne fait pas partie de ce groupe, ni les pierres blanches 7 et 8 . Ce groupe a 7 libertés. La pierre 9 a 3 libertés. Le groupe de pierre 10, 11, 12 a une seule liberté, si Blanc joue en ( 7,7 ) alors il capture immédiatement ce groupe, et les pierres 10, 11, 12 sont retirées du plateau. L'intersection
Cette règle de capture permet d'aboutir à des configurations avec moins de pierres sur le goban. Afin de s'assurer que la partie termine, une règle supplémentaire interdit de jouer un coup qui fasse revenir à une configuration du goban déjà vue durant la partie.
Lorsqu'une pierre est placée, on commence par regarder si elle permet de capturer des pierres adverses, et dans ce cas on retire immédiatement ces pierres capturées du goban. On regarde ensuite si le groupe de la pierre placée possède des libertés. Si elle ne possède aucune liberté, le coup est interdit. Cependant, si elle a permis de capturer des pierres, son groupe a nécessairement au moins une liberté. Il est donc possible de jouer sur une position sans libertés, mais uniquement dans le cas où cela permet de capturer des pierres à l'adversaire.
Une intersection est dite contrôlée par un joueur si une de ses pierres est placée dessus, ou si l'intersection est vide mais que toutes les intersections voisines contiennent des pierres de sa couleur.
La partie s'arrête lorsque toutes les intersections sont contrôlées par un des deux joueurs. Une telle configuration du goban est alors dite finale. Le score de chaque joueur est défini comme le nombre d'intersections contrôlées par ce dernier. Le joueur avec le score le plus élevé remporte la partie.
Lorsqu'une pierre est placée, on commence par regarder si elle permet de capturer des pierres adverses, et dans ce cas on retire immédiatement ces pierres capturées du goban. On regarde ensuite si le groupe de la pierre placée possède des libertés. Si elle ne possède aucune liberté, le coup est interdit. Cependant, si elle a permis de capturer des pierres, son groupe a nécessairement au moins une liberté. Il est donc possible de jouer sur une position sans libertés, mais uniquement dans le cas où cela permet de capturer des pierres à l'adversaire.
Une intersection est dite contrôlée par un joueur si une de ses pierres est placée dessus, ou si l'intersection est vide mais que toutes les intersections voisines contiennent des pierres de sa couleur.
La partie s'arrête lorsque toutes les intersections sont contrôlées par un des deux joueurs. Une telle configuration du goban est alors dite finale. Le score de chaque joueur est défini comme le nombre d'intersections contrôlées par ce dernier. Le joueur avec le score le plus élevé remporte la partie.
I.C - Généralités sur le jeu de go
Q 1. Compter le nombre de libertés du groupe auquel appartient la pierre D dans le goban de la figure 2 Droite. Donner le score de Blanc, celui de Noir et le joueur gagnant de cette partie.
Q 2. Montrer qu'il y a toujours un gagnant dans une configuration finale sur un goban standard de dimension 19.
Q 2. Montrer qu'il y a toujours un gagnant dans une configuration finale sur un goban standard de dimension 19.
II Implémentation du jeu de go
L'objectif de cette première partie est d'implémenter diverses fonctions permettant de manipuler le goban pour mener une partie de go. Ces fonctions sont à écrire en langage
#include <assert.h>
#include <stdbool.h>
#include <stddef.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
Afin de représenter et manipuler un goban, nous utiliserons la structure de données suivante pour représenter une configuration.
struct goban_s {
int d;
int* m;
};
typedef struct goban_s goban;
Le champ d est ici la dimension du goban, et
Q 3. Écrire une fonction goban initialisation(int d) prenant en argument un entier d et qui renvoie un goban de dimension
La position d'une intersection du goban sera représentée par une structure de couple d'entiers, contenant la ligne
Q 3. Écrire une fonction goban initialisation(int d) prenant en argument un entier d et qui renvoie un goban de dimension
La position d'une intersection du goban sera représentée par une structure de couple d'entiers, contenant la ligne
struct couple_int {
int i;
int j;
};
typedef struct couple_int position;
Une position pourra être initialisée avec la fonction suivante :
position pos(int i, int j) {
position p = {.i = i, .j = j};
return p;
}
Un goban pourra être lu et modifié grâce aux deux fonctions ci-dessous, en supposant que la position correspond à une intersection valide du goban.
int lire(goban g, position p) {
return g.m[p.i * g.d + p.j];
}
void ecrire(goban g, position p, int couleur) {
g.m[p.i * g.d + p.j] = couleur;
}
Les questions suivantes vont permettre d'isoler un groupe de pierres. Pour cela, nous représentons les intersections voisines d'une intersection donnée grâce à la structure suivante :
struct voisins_s {
int nb;
position t[4];
};
typedef struct voisins_s voisins;
Le nombre de voisins de l'intersection est donné par le champ nb, et t est un tableau de positions de taille 4, dont les nb premières cases contiennent les positions des intersections voisines de l'intersection. La fonction incomplète suivante permet ce calcul des voisins :
voisins pos_voisins(goban g, position p) {
int i = p.i;
int j = p.j;
voisins v;
if (...) {v.t[k] = pos(i - 1, j); k = k + 1;}
if (...) {v.t[k] = pos(i + 1, j); k = k + 1;}
if (...) {v.t[k] = pos(i, j - 1); k = k + 1;}
if (...) {v.t[k] = pos(i, j + 1); k = k + 1;}
v.nb = k;
return v;
}
Q 4. Compléter cette fonction pos_voisins en donnant l'instruction à écrire en ligne 5 ainsi que les conditions à écrire pour chacune des lignes
Q 5. Écrire une fonction goban groupe (goban g, position p) qui renvoie un nouveau goban dans lequel seules les pierres du groupe de la pierre en position p sont présentes. Expliquer par une phrase, avant le code de votre fonction, l'approche choisie. Il pourra être utile de commencer par implémenter une fonction auxiliaire récursive, dont la spécification sera clairement explicitée. Donner la complexité obtenue.
Une première tentative pour calculer le nombre de libertés du groupe de la pierre en position
Q 5. Écrire une fonction goban groupe (goban g, position p) qui renvoie un nouveau goban dans lequel seules les pierres du groupe de la pierre en position p sont présentes. Expliquer par une phrase, avant le code de votre fonction, l'approche choisie. Il pourra être utile de commencer par implémenter une fonction auxiliaire récursive, dont la spécification sera clairement explicitée. Donner la complexité obtenue.
Une première tentative pour calculer le nombre de libertés du groupe de la pierre en position
int liberte(goban g, position p) {
goban g1 = groupe(g, p);
int cpt = 0;
int couleur = lire(g, p);
for (int i = 0; i < g.d; i = i + 1) {
for (int j = 0; j < g.d; j = j + 1) {
position p2 = pos(i, j);
if (lire(g1, p2) == couleur) {
voisins v = pos_voisins(g1, p2);
for (int k = 0; k < v.nb; k = k + 1) {
if (lire(g, v.t[k]) == 0) {
cpt = cpt + 1;
}
}
}
}
}
return cpt;
}
Q 6. Proposer un jeu de quatre tests permettant de tester cette fonction liberte. Deux tests seront passés par la fonction, et deux montreront qu'elle n'est pas correcte. Les gobans en entrées pourront être représentés par des schémas. On prendra soin de justifier l'intérêt des tests proposés et d'indiquer les valeurs attendues.
Q 7. Proposer des modifications à apporter au code de la fonction liberte pour qu'elle renvoie bien le nombre de libertés, et qu'elle libère les structures créées pendant son appel.
Q 8. Écrire une fonction void retire_groupe(goban g, position p) prenant en argument un goban, une position et qui retire toutes les pierres du groupe de la pierre à cette position. Une complexité linéaire en la taille du groupe à retirer est attendue.
Q 9. Écrire une fonction void joue (goban g, position p, int couleur) prenant en argument un goban, une position et une couleur et qui modifie le goban en ajoutant une pierre de la couleur donnée à la position donnée. On prendra en compte les possibles pierres à retirer et on utilisera des assertions pour vérifier que le coup est valable. On ne vérifiera cependant pas si la configuration du goban a déjà été rencontrée au cours de la partie. Donner la complexité de cette fonction.
Q 7. Proposer des modifications à apporter au code de la fonction liberte pour qu'elle renvoie bien le nombre de libertés, et qu'elle libère les structures créées pendant son appel.
Q 8. Écrire une fonction void retire_groupe(goban g, position p) prenant en argument un goban, une position et qui retire toutes les pierres du groupe de la pierre à cette position. Une complexité linéaire en la taille du groupe à retirer est attendue.
Q 9. Écrire une fonction void joue (goban g, position p, int couleur) prenant en argument un goban, une position et une couleur et qui modifie le goban en ajoutant une pierre de la couleur donnée à la position donnée. On prendra en compte les possibles pierres à retirer et on utilisera des assertions pour vérifier que le coup est valable. On ne vérifiera cependant pas si la configuration du goban a déjà été rencontrée au cours de la partie. Donner la complexité de cette fonction.
III Prédiction et évaluation d'un prochain coup
Dans cette partie, nous envisageons de réaliser un programme qui renvoie ou évalue un prochain coup pertinent à jouer depuis une configuration donnée du goban, afin de simuler un adversaire. La dimension stratégique du jeu de go est réputée pour être complexe, c'est pourquoi une première approche simple peut être de s'inspirer de coups joués par des joueurs humains professionnels.
Pour cela nous nous baserons sur une base de données de 160000 parties de maîtres, jouées sur des gobans standards de dimension 19. Nous avons commencé par décomposer ces parties en 29.4 millions de triplets (configuration du goban, joueur dont c'est le tour, coup suivant choisi), que nous appellerons observations, et qui peuvent être redondantes.
Q 10. À partir des informations sur la base de données, donner une estimation de la profondeur du jeu de go, c'est-à-dire du nombre de coups moyen d'une partie de go. En utilisant la description du jeu ainsi que la profondeur, donner une estimation de la largeur du jeu de go, c'est-à-dire le nombre moyen de coups valables lors d'une partie.
Est-il envisageable de mettre en place un algorithme min-max pour trouver une stratégie gagnante à ce jeu? Justifier.
Pour cela nous nous baserons sur une base de données de 160000 parties de maîtres, jouées sur des gobans standards de dimension 19. Nous avons commencé par décomposer ces parties en 29.4 millions de triplets (configuration du goban, joueur dont c'est le tour, coup suivant choisi), que nous appellerons observations, et qui peuvent être redondantes.
Q 10. À partir des informations sur la base de données, donner une estimation de la profondeur du jeu de go, c'est-à-dire du nombre de coups moyen d'une partie de go. En utilisant la description du jeu ainsi que la profondeur, donner une estimation de la largeur du jeu de go, c'est-à-dire le nombre moyen de coups valables lors d'une partie.
Est-il envisageable de mettre en place un algorithme min-max pour trouver une stratégie gagnante à ce jeu? Justifier.
III.A - K plus proches voisins
Afin de jouer en un temps raisonnable, dans cette sous-partie nous allons implémenter l'algorithme des
Q 11. Proposer une fonction double* k_plus_petits (double* distances, int n, int k) qui prend en entrée un tableau de
Q 12. Proposer une structure de données abstraite qui permette d'améliorer la complexité asymptotique de la fonction k_plus_petits. Rappeler en une phrase une façon d'implémenter cette structure de données ainsi que la complexité obtenue.
Dans le cadre d'un adversaire jouant en temps réel, il est préférable d'avoir une borne précise sur le nombre de comparaisons qui seront réalisées. Nous supposerons désormais que
Nous appellerons comparatif un algorithme prenant en entrée un tableau de distances pour lequel la seule opération autorisée sur les distances du tableau est la comparaison entre deux distances du tableau.
Q 13. Montrer que tout algorithme comparatif renvoyant l'indice du plus petit élément d'un tableau devra réaliser la comparaison du plus petit élément et du second plus petit élément du tableau.
Q 14. Proposer un algorithme qui renvoie les indices des deux plus petits éléments d'un tableau de
Q 11. Proposer une fonction double* k_plus_petits (double* distances, int n, int k) qui prend en entrée un tableau de
Q 12. Proposer une structure de données abstraite qui permette d'améliorer la complexité asymptotique de la fonction k_plus_petits. Rappeler en une phrase une façon d'implémenter cette structure de données ainsi que la complexité obtenue.
Dans le cadre d'un adversaire jouant en temps réel, il est préférable d'avoir une borne précise sur le nombre de comparaisons qui seront réalisées. Nous supposerons désormais que
Nous appellerons comparatif un algorithme prenant en entrée un tableau de distances pour lequel la seule opération autorisée sur les distances du tableau est la comparaison entre deux distances du tableau.
Q 13. Montrer que tout algorithme comparatif renvoyant l'indice du plus petit élément d'un tableau devra réaliser la comparaison du plus petit élément et du second plus petit élément du tableau.
Q 14. Proposer un algorithme qui renvoie les indices des deux plus petits éléments d'un tableau de
III.B - Hachage de Zobrist
Le but de cette sous-partie est de présenter une autre approche utilisant la base de données des parties de maîtres, cette fois pour apprendre une fonction d'évaluation des prochains coups qui s'intéresse uniquement à l'état local du goban autour d'une position envisagée. Nous chercherons, dans la base de données, si des configurations localement identiques ont mené à un coup à cette position. Cette recherche sera implémentée de manière efficace dans cette partie grâce à un prétraitement de la base de données utilisant des tables de hachage et une fonction de hachage adaptée, nommée hachage de Zobrist.
Un état local sera modélisé par différents zooms autour d'une position, qui considèrent la disposition du plateau autour d'une intersection en ignorant le reste du goban, appelée motif. Nous noterons
Le but d'un zoom sur une position est d'évaluer un coup potentiel à cette position. Étant donné un motif centré sur une intersection libre sur laquelle il est possible de jouer, nous allons chercher dans la base de données si des configurations possédant ce même motif ont mené à un coup à cette position. Nous considérerons toujours que le centre du motif est une intersection vide.
Q 15. Donner une borne supérieure sur le nombre de motifs distincts pour un zoom
Les fonctions de cette partie sont à écrire en langage
Pour savoir combien de fois un motif a conduit à un coup en son centre, nous allons construire et remplir une table de hachage, pour chaque niveau de zoom. La fonction de hachage associée assignera à chaque motif un entier non signé de 64 bits, de type uint64_t. Cette fonction de hachage particulière se base sur une table d'entiers uint64_t fixés, ayant autant de colonnes que de positions dans le motif, et quatre lignes pour les quatre
Un état local sera modélisé par différents zooms autour d'une position, qui considèrent la disposition du plateau autour d'une intersection en ignorant le reste du goban, appelée motif. Nous noterons
Le but d'un zoom sur une position est d'évaluer un coup potentiel à cette position. Étant donné un motif centré sur une intersection libre sur laquelle il est possible de jouer, nous allons chercher dans la base de données si des configurations possédant ce même motif ont mené à un coup à cette position. Nous considérerons toujours que le centre du motif est une intersection vide.
Q 15. Donner une borne supérieure sur le nombre de motifs distincts pour un zoom
Les fonctions de cette partie sont à écrire en langage
Pour savoir combien de fois un motif a conduit à un coup en son centre, nous allons construire et remplir une table de hachage, pour chaque niveau de zoom. La fonction de hachage associée assignera à chaque motif un entier non signé de 64 bits, de type uint64_t. Cette fonction de hachage particulière se base sur une table d'entiers uint64_t fixés, ayant autant de colonnes que de positions dans le motif, et quatre lignes pour les quatre
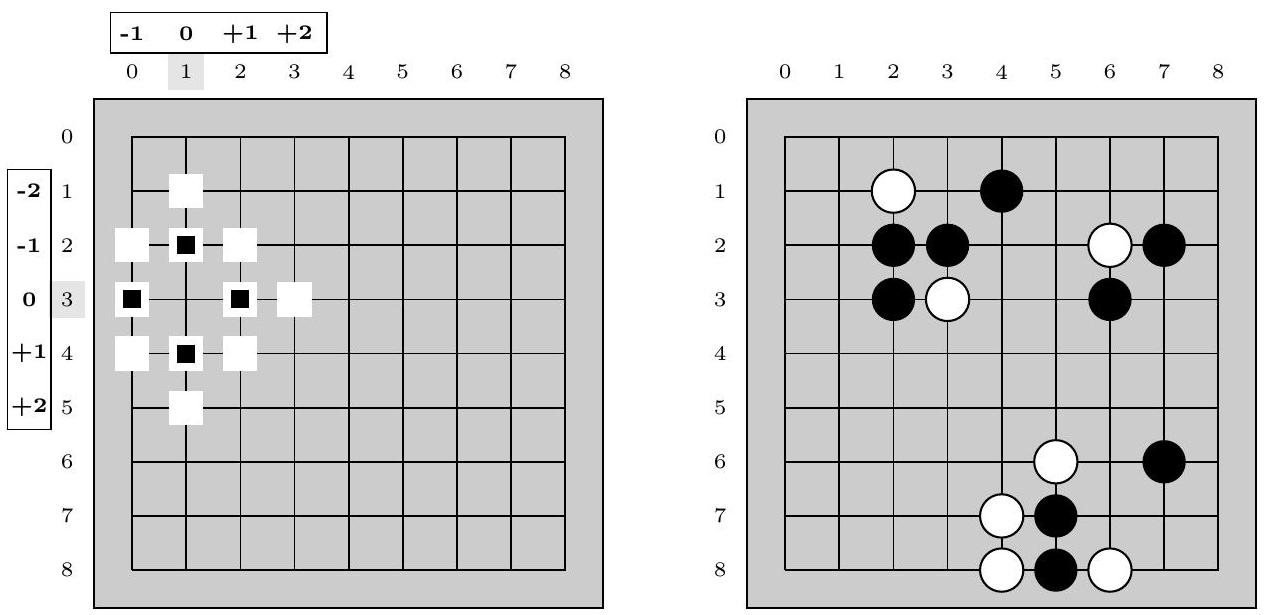
Figure 3 Gauche : l'étendue du zoom 1 (les 4 intersections avec un carré noir), et du zoom 2 (les 11 intersections avec des carrés blancs, et une intersection extérieure à la grille non représentée) sur la position
Droite: un exemple de goban. Les motifs correspondant au zoom 1 en position ( 2,4 ) et au zoom 1 en position ( 3,7 ) sont identiques, ce motif est ici observé deux fois dans cette configuration. Si Noir choisit de jouer en
couleurs possibles (libre, noir, blanc et hors du goban). Afin de manipuler à la main un nombre raisonnable de bits, sur la table donnée en exemple en figure 4 , nous utilisons des entiers codés sur 8 bits et non sur 64 bits La valeur de hachage est alors calculée comme le ou exclusif (XOR) bit à bit, noté
Formellement, en notant
couleurs possibles (libre, noir, blanc et hors du goban). Afin de manipuler à la main un nombre raisonnable de bits, sur la table donnée en exemple en figure 4 , nous utilisons des entiers codés sur 8 bits et non sur 64 bits La valeur de hachage est alors calculée comme le ou exclusif (XOR) bit à bit, noté
Formellement, en notant
| a | b | a XOR b |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
| Couleur et position |
|
|
(0, -1) | (
|
| 0 (vide) | 00001111 | 11100111 | 00011000 | 01111011 |
| 1 (noir) | 11110110 | 11111110 | 01101001 | 10011111 |
| 2 (blanc) | 10100001 | 10001101 | 00110111 | 00110100 |
| 3 (au delà du bord) | 10100000 | 01101010 | 10111011 | 11000010 |
Figure 4 Table de vérité du XOR, et une table d'entiers fixés sur 8 bits associés à des couples couleur et position dans le motif. Par exemple une pierre noire en position (
Q 16. Dans le goban de la figure 3 Droite, et avec le tableau de valeurs sur 8 bits donné dans la figure 4, calculer la valeur de hachage du motif en position
Nous disposons désormais d'une fonction uint64_t hachage(position p, goban g, int zoom) qui calcule la valeur de hachage
De plus, en connaissant la valeur de hachage
Nous nous intéressons maintenant uniquement aux choix des coups de Noir. Il nous faut dénombrer les motifs observés et les motifs choisis dans la base de données de parties. Pour un niveau de zoom fixé, nous stockerons ces valeurs dans une table de hachage, associant un motif à son nombre d'observations et de choix.
Pour un niveau de zoom fixé, dans une configuration du goban où c'est au tour de Noir de jouer, nous observons un motif par position libre de cette configuration. Noir va alors jouer dans une de ces positions libres, et on dit que le motif associé à la position libre où Noir joue est choisi (voir la figure 3).
Nous disposons désormais d'une fonction uint64_t hachage(position p, goban g, int zoom) qui calcule la valeur de hachage
De plus, en connaissant la valeur de hachage
Nous nous intéressons maintenant uniquement aux choix des coups de Noir. Il nous faut dénombrer les motifs observés et les motifs choisis dans la base de données de parties. Pour un niveau de zoom fixé, nous stockerons ces valeurs dans une table de hachage, associant un motif à son nombre d'observations et de choix.
Pour un niveau de zoom fixé, dans une configuration du goban où c'est au tour de Noir de jouer, nous observons un motif par position libre de cette configuration. Noir va alors jouer dans une de ces positions libres, et on dit que le motif associé à la position libre où Noir joue est choisi (voir la figure 3).
Pour chaque niveau de zoom, les valeurs stockées dans sa table de hachage associée seront représentées par la structure suivante:
struct observation_s {
int n; //nombre d'observations du motif au total
int v; //nombre de fois ou ce motif a ete choisi
};
typedef struct observation_s observation;
Le champ n correspond au nombre d'observations du motif dans des gobans où c'était à Noir de jouer. Le champ v correspond au nombre de fois où le motif était observé au moment où c'était à Noir de jouer et où le coup de Noir a été de placer une pierre au centre de ce motif.
Nous définissons alors une structure de table de hachage composée d'un tableau d'observations, et d'un entier nt correspondant à sa taille.
Nous définissons alors une structure de table de hachage composée d'un tableau d'observations, et d'un entier nt correspondant à sa taille.
struct table_de_hachage_s {
int nt;
observation* t;
};
typedef struct table_de_hachage_s t_hachage;
La table de hachage est initialisée avec
Pour remplir la table de hachage, nous allons simuler la partie de maître configuration après configuration, en utilisant la fonction maj_hachage pour mettre à jour les valeurs de hachages. Au départ, nous partons donc de la configuration initiale du goban, et nous allons garder en mémoire les valeurs de hachage pour chaque position du goban, et les faire évoluer au fur et à mesure de la partie.
Q 17. Écrire une fonction uint64_t* init_t_hash (int d, int zoom) qui prend en entrée un entier d correspondant à la dimension d'un goban, et un entier zoom correspondant au niveau de zoom d'intérêt, et qui renvoie un tableau d'entiers non signés sur 64 bits alloué dynamiquement, de taille
On considère un goban
Pour remplir la table de hachage, nous allons simuler la partie de maître configuration après configuration, en utilisant la fonction maj_hachage pour mettre à jour les valeurs de hachages. Au départ, nous partons donc de la configuration initiale du goban, et nous allons garder en mémoire les valeurs de hachage pour chaque position du goban, et les faire évoluer au fur et à mesure de la partie.
Q 17. Écrire une fonction uint64_t* init_t_hash (int d, int zoom) qui prend en entrée un entier d correspondant à la dimension d'un goban, et un entier zoom correspondant au niveau de zoom d'intérêt, et qui renvoie un tableau d'entiers non signés sur 64 bits alloué dynamiquement, de taille
On considère un goban
void maj_coup(t_hachage table, uint64_t* tableau_hache, goban gN, goban gB, int zoom) {
for (int i = 0; i < gN.d; i = i + 1) {
for (int j = 0; j < gN.d; j = j + 1) {
position p = pos(i, j);
maj_n(table, tableau_hache, gN, p);
maj_v(table, tableau_hache, gN, gB, p);
}
}
}
void maj_t_hache(uint64_t* tableau_hache, goban gN, goban gNs, int zoom) {
for (int i = 0; i < gN.d; i = i + 1) {
for (int j = 0; j < gN.d; j = j + 1) {
position p = pos(i, j);
maj_h(tableau_hache, gN, gNs, zoom, p);
}
}
}
Q 18. Écrire les fonctions
void maj_n(t_hachage table, uint64_t* tableau_hache, goban gN, position p),
void maj_v(t_hachage table, uint64_t* tableau_hache, goban gN, goban gB, position p),
void maj_h(uint64_t* tableau_hache, goban gN, goban gNs, int zoom, position p),
pour que les fonctions maj_coup et maj_t_hache mettent correctement à jour la table de hachage et le tableau
des valeurs de hachage.
Une partie de go sera représentée par une structure de liste simplement chaînée, chaque coup étant représenté par le goban actuel, le joueur qui doit jouer, et un pointeur vers le reste de la partie. Nous supposerons que les parties commencent par le goban vide associé au joueur d'indice 1 (Noir).
struct partie_s {
goban g;
int joueur;
struct partie_s* suivant;
};
typedef struct partie_s partie;
Q 19. En s'intéressant uniquement aux coups de Noir, écrire une fonction t_hachage lit_partie(partie* lp, int zoom, t_hachage table) qui prend en entrée une partie et met à jour pour le zoom donné et dans toutes les positions libres du goban le nombre d'occurrences des motifs, et le nombre de choix des motifs choisis, dans la table de hachage donnée en entrée (qui a déjà été initialisée et mise à jour sur d'autres parties). On pourra supposer que la partie contient au moins 3 coups.
Q 20. Étant donné un tableau des valeurs de hachage initialisé avec le goban initial, montrer qu'au plus
Nous allons représenter toutes les tables de hachages pour les différents niveaux de zoom allant de 1 à
Q 20. Étant donné un tableau des valeurs de hachage initialisé avec le goban initial, montrer qu'au plus
Nous allons représenter toutes les tables de hachages pour les différents niveaux de zoom allant de 1 à
struct table_table_de_hachage {
int nz;
t_hachage* t;
};
typedef struct table_table_de_hachage tt_hachage;
Nous construisons cette table de tables de hachages tt telle que
Pour évaluer la pertinence d'un coup dans une configuration, nous allons chercher le plus grand zoom pour lequel le motif a été observé au moins une fois dans la base de données. La qualité estimée de ce coup est alors le nombre de fois où ce motif a été choisi sur le nombre de fois où il a été vu.
Q 21. Écrire une fonction booléenne bool appartient(position p, goban g, t_hachage table, int zoom) qui renvoie vrai si le motif en position
Q 22. Écrire une fonction float evalue_zoom (position p, goban g, t_hachage table, int zoom) qui renvoie la valeur associée au motif, c'est-à-dire le rapport entre le nombre d'observations et le nombre de choix.
Q 23. Écrire une fonction float evaluation(position p, goban g, tt_hachage tt ) qui renvoie l'évaluation du coup en position p sur le goban g. Une fonction de complexité logarithmique en le nombre de zooms
Pour évaluer la pertinence d'un coup dans une configuration, nous allons chercher le plus grand zoom pour lequel le motif a été observé au moins une fois dans la base de données. La qualité estimée de ce coup est alors le nombre de fois où ce motif a été choisi sur le nombre de fois où il a été vu.
Q 21. Écrire une fonction booléenne bool appartient(position p, goban g, t_hachage table, int zoom) qui renvoie vrai si le motif en position
Q 22. Écrire une fonction float evalue_zoom (position p, goban g, t_hachage table, int zoom) qui renvoie la valeur associée au motif, c'est-à-dire le rapport entre le nombre d'observations et le nombre de choix.
Q 23. Écrire une fonction float evaluation(position p, goban g, tt_hachage tt ) qui renvoie l'évaluation du coup en position p sur le goban g. Une fonction de complexité logarithmique en le nombre de zooms
IV Recherche arborescente de Monte-Carlo
Dans cette partie nous nous intéressons à la construction d'un programme en OCaml jouant au go, en utilisant l'approche de Recherche Arborescente de Monte-Carlo. C'est notamment sur cette méthode que s'est basé AlphaGo pour vaincre le champion du monde de go en 2017. Nous supposerons dans cette section que les parties de go finissent toujours dans une configuration finale, c'est-à-dire complètement contrôlée, sans égalité et que le goban est de dimension standard
Les fonctions de cette partie sont à écrire en langage OCaml. Une annexe rappelant des éléments de langage OCaml, modules Thread et Mutex, module List, type enregistrement et fonction de conversion de type, est proposée en fin de partie.
Commençons par décrire quatre types pour représenter les joueurs, les gobans et les positions:
Les fonctions de cette partie sont à écrire en langage OCaml. Une annexe rappelant des éléments de langage OCaml, modules Thread et Mutex, module List, type enregistrement et fonction de conversion de type, est proposée en fin de partie.
Commençons par décrire quatre types pour représenter les joueurs, les gobans et les positions:
type joueur = Noir | Blanc
type intersection = Libre | Pierre_noire | Pierre_blanche
type goban = intersection array array
type position = int * int
Nous supposerons que les fonctions suivantes ont été déjà implémentées et peuvent être librement utilisées.
- liste_coup_prior : goban -> joueur -> (position * float) list: prend un goban et un joueur et renvoie une liste, pour toutes les positions jouables dans le goban pour le joueur, de couples (position, prior) où prior est un flottant entre 0 et 1 correspondant à une estimation de la probabilité de victoire de Noir lorsque le joueur joue en position position.
- strategie_defaut : goban -> joueur -> position: prend un goban et un joueur et renvoie une position où jouer, en suivant une stratégie par défaut définie a priori, et qui peut contenir une part d'aléatoire. Cette fonction renvoie l'exception Pas_de_coup_valide lorsque le plateau est complètement contrôlé et qu'il n'y a plus de coup valide.
- gagnant : goban -> joueur : prend un goban complètement contrôlé et renvoie le joueur gagnant.
- joue : goban -> position -> joueur -> goban: prend un goban, une position et un joueur et renvoie le goban obtenu après que le joueur a joué en cette position. Le goban en entrée n'est pas modifié.
Q 24. Écrire une fonction de signature js : joueur -> joueur qui prend un joueur et renvoie le joueur suivant.
IV.A - Simulation de partie pour évaluer une configuration
Pour trouver un prochain coup pertinent, il est important de pouvoir évaluer si une configuration du goban est prometteuse ou non, ce qui est une tâche complexe. L'évaluation de Monte-Carlo permet d'estimer cette évaluation de goban, en jouant une partie depuis la configuration actuelle jusqu'au bout, et en choisissant les coups successifs grâce à une stratégie définie a priori. Celle-ci peut-être complètement aléatoire, ou basée sur des données d'apprentissage par exemple.
Q 25. Écrire une fonction de signature sim_defaut : goban
Q 25. Écrire une fonction de signature sim_defaut : goban
IV.B - Valeur d'action
Dans la recherche arborescente de Monte-Carlo, nous explorons l'arbre de toutes les parties possibles depuis le goban actuel, mais sans stocker explicitement cet arbre tout entier. De multiples explorations sont réalisées partant chacune de la racine de l'arbre et descendant jusqu'à une configuration finale, sans représentation explicite de l'arbre, en suivant des stratégies définies a priori. L'idée principale de la recherche arborescente de Monte-Carlo est d'ajouter à cette approche sans mémoire la construction d'un arbre partiel de jeu, dont les nœuds vont correspondre aux configurations souvent explorées, et pour lesquelles il sera possible d'enregistrer différentes informations:
- n : le nombre de visites du nœud, entier mutable
- v: le nombre de visites du nœud ayant mené à une victoire de Noir, entier mutable
- prior : la probabilité a priori de victoire de Noir donnée par la fonction liste_coups_prior, flottant
- pos: la position du coup associé au nœud, position
- t : un verrou, de type t . Mutex, qui sera utilisé pour mettre en place des parcours et mises à jour concurrentes de l'arbre.
Afin de stocker ces données, les nœuds de l'arbre seront étiquetés par le type enregistrement etiquette.
type etiquette =
{mutable n:int; mutable v:int; prior:float; pos:position; t:Mutex.t}
Enfin, nous définissons le type suivant pour l'arbre partiel:
1 type arbre = N of etiquette * arbre list
La première étape de la recherche arborescente de Monte-Carlo est une descente qui consiste à suivre un chemin dans l'arbre partiel qui semble prometteur jusqu'à atteindre une feuille. Pour un nœud
Cette valeur est un compromis entre la prior apprise par apprentissage et le taux de victoires obtenu lors des descentes dans l'arbre, l'importance de la prior décroissant avec l'augmentation du nombre de descentes dans l'arbre passant par le nœud. Une valeur d'action analogue peut être définie pour Blanc. En partant de la racine de l'arbre partiel, la feuille à explorer est atteinte en descendant le long d'une branche, en choisissant itérativement comme nœud suivant le fils de valeur d'action maximale pour le joueur qui doit jouer.
Q 26. Écrire une fonction de signature etiq : arbre -> etiquette qui prend un arbre et renvoie l'étiquette de cette arbre.
Q 27. Écrire une fonction de signature valeurActionNoir : arbre
Q 28. Donner la valeur à maximiser au tour de Blanc en suivant le même principe que pour la valeur d'action de Noir. Nous supposerons par la suite que la fonction valeurActionBlanc : arbre -> float a été également implémentée.
Q 29. Écrire une fonction de signature popargmax : 'a list
Q 26. Écrire une fonction de signature etiq : arbre -> etiquette qui prend un arbre et renvoie l'étiquette de cette arbre.
Q 27. Écrire une fonction de signature valeurActionNoir : arbre
Q 28. Donner la valeur à maximiser au tour de Blanc en suivant le même principe que pour la valeur d'action de Noir. Nous supposerons par la suite que la fonction valeurActionBlanc : arbre -> float a été également implémentée.
Q 29. Écrire une fonction de signature popargmax : 'a list
IV.C - Descente et remontée dans l'arbre
Pour affiner les évaluations des configurations stockées dans l'arbre partiel, la recherche arborescente de MonteCarlo procède en trois étapes clés :
- une descente dans l'arbre partiel en choisissant à chaque nœud le fils de valeur d'action maximale pour le joueur associé, afin de sélectionner une feuille qui semble prometteuse;
- une simulation de partie depuis cette feuille comme implémentée en partie IV.A, donnant un joueur vainqueur ;
- une remontée qui met à jour le nombre d'observations et de victoires pour Noir dans chaque nœud rencontré, le long de la branche reliant la feuille explorée à la racine de l'arbre.
Ces étapes pourront être exécutées en parallèles par plusieurs fils d'exécution. Il est donc nécessaire de faire attention à ce que deux fils ne rentrent pas en conflit d'écriture et de lecture pour un champ mutable d'une étiquette de l'arbre, ce qui justifie l'intérêt des verrous associés à chaque nœud.
De plus, pour décourager deux fils d'exécution de suivre la même branche lors de la descente, lorsque l'enfant d'un nœud est sélectionné par un fil d'exécution, ce fil va modifier l'étiquette de cet enfant pour lui ajouter des défaites virtuelles, ce qui baissera sa valeur d'action et donc son attractivité du point de vue des autres fils. Nous ajouterons 5 défaites virtuelles à un nœud s'il est sélectionné, en prenant soin d'enlever ces défaites virtuelles lors de la remontée.
Lors de la descente, nous empêcherons ainsi un fil d'exécution de commencer à traiter un nœud, (c'est-à-dire de chercher l'enfant de ce nœud de valeur d'action maximale) si un autre fil d'exécution est déjà en train de traiter ce nœud. Nous attendrons que le fil d'exécution en cours ait ajouté des défaites virtuelles à la branche qu'il a choisi de suivre avant de commencer le traitement.
Q 30. Écrire la fonction descente_remontee_arbre : gobanjoueur arbre joueur qui prend un goban, le joueur dont c'est le tour et un arbre de jeu, et qui réalise une descente, une simulation et une remontée de l'arbre. Cette fonction renverra le joueur gagnant, et lors de la remontée mettra à jour les champs mutables des nœuds rencontrés. Une attention particulière sera portée sur le fait que cette fonction puisse être exécutée par plusieurs fils d'exécution concurrents.
IV.D - Expansion de l'arbre
L'idée de la recherche arborescente de Monte-Carlo est d'alterner entre des étapes de descente, simulation et remontée de l'arbre pour améliorer les évaluations des nœuds, et des étapes d'expansion, où nous ajoutons de nouveaux nœuds à l'arbre partiel de jeu.
Q 31. Écrire une fonction de signature expansion_feuille : goban
Une étape d'expansion consiste à étendre une feuille, qui sera sélectionnée en partant de la racine et en choisissant à chaque nœud le fils ayant été le plus visité.
Q 31. Écrire une fonction de signature expansion_feuille : goban
Une étape d'expansion consiste à étendre une feuille, qui sera sélectionnée en partant de la racine et en choisissant à chaque nœud le fils ayant été le plus visité.
Q 32. Écrire une fonction de signature expansion : goban
IV.E - Algorithme complet
Pour pouvoir commencer à réaliser l'étape d'expansion, il est nécessaire d'attendre que tous les fils d'exécution réalisant des descentes et remontées aient terminé.
Q 33. Écrire une fonction de signature attendre : Thread.t list
Q 34. Écrire une fonction de signature etape_complete : int
Q 35. Montrer que cette fonction termine. Il est notamment attendu de montrer qu'il n'y a pas d'interblocages dans les exécutions de la fonction descente_remontee_arbre en se référant au code proposé en question 30.
Pour estimer le coup à jouer, il reste alors à réaliser plusieurs étapes complètes, par exemple un nombre ns fixé à l'avance. Puis, à la fin de ces étapes, l'algorithme renvoie la position du coup correspondant au nœud le plus visité parmi les fils de la racine.
Le sous-arbre associé à ce coup sera ensuite utilisé comme base pour la suite de la partie, ce qui permet de ne pas repartir de zéro à chaque coup.
Q 36. Écrire une fonction de signature recherche_arborescente : int -> int -> goban -> joueur -> arbre -> arbre * position telle que recherche_arborescente ns nt g j a effectue ns étapes de simulations sur l'arbre a en partant du goban
Q 33. Écrire une fonction de signature attendre : Thread.t list
Q 34. Écrire une fonction de signature etape_complete : int
Q 35. Montrer que cette fonction termine. Il est notamment attendu de montrer qu'il n'y a pas d'interblocages dans les exécutions de la fonction descente_remontee_arbre en se référant au code proposé en question 30.
Pour estimer le coup à jouer, il reste alors à réaliser plusieurs étapes complètes, par exemple un nombre ns fixé à l'avance. Puis, à la fin de ces étapes, l'algorithme renvoie la position du coup correspondant au nœud le plus visité parmi les fils de la racine.
Le sous-arbre associé à ce coup sera ensuite utilisé comme base pour la suite de la partie, ce qui permet de ne pas repartir de zéro à chaque coup.
Q 36. Écrire une fonction de signature recherche_arborescente : int -> int -> goban -> joueur -> arbre -> arbre * position telle que recherche_arborescente ns nt g j a effectue ns étapes de simulations sur l'arbre a en partant du goban
Éléments du langage OCaml
Module Thread
Thread.t : Le type des fils d'exécution.
Thread.create : ('a -> 'b) -> 'a -> Thread.t: Thread.create funct arg crée un nouveau fil d'exécution dans lequel l'application de funct arg est exécuté en même temps que les autres fils d'exécutions. L'application de Thread.create renvoie le fil d'exécution crée. Le nouveau fil termine quand l'application funct arg termine, soit normalement soit en remontant une exception Thread.Exit ou en remontant d'autres exceptions non rattrapées. Dans ce dernier cas, l'exception non rattrapée est affichée sur la sortie d'erreur standard, mais pas propagée au fil d'exécution parent. De la même manière le résultat de l'application funct arg est perdu et n'est pas directement accessible au fil d'exécution parent.
Thread.join :
Thread.t : Le type des fils d'exécution.
Thread.create : ('a -> 'b) -> 'a -> Thread.t: Thread.create funct arg crée un nouveau fil d'exécution dans lequel l'application de funct arg est exécuté en même temps que les autres fils d'exécutions. L'application de Thread.create renvoie le fil d'exécution crée. Le nouveau fil termine quand l'application funct arg termine, soit normalement soit en remontant une exception Thread.Exit ou en remontant d'autres exceptions non rattrapées. Dans ce dernier cas, l'exception non rattrapée est affichée sur la sortie d'erreur standard, mais pas propagée au fil d'exécution parent. De la même manière le résultat de l'application funct arg est perdu et n'est pas directement accessible au fil d'exécution parent.
Thread.join :
Module Mutex
Mutex.t: Le type des mutex.
Mutex.create : unit $\rightarrow$ Mutex.t: Renvoie un nouveau mutex.
Mutex.lock : Mutex.t -> unit: Verrouille le mutex donné. Un seul fil d'exécution peut verrouiller le
mutex à un moment donné. Un fil d'exécution tentant de verrouiller un mutex déjà verrouillé attendra
jusqu'à ce que l'autre fil d'exécution déverouille le mutex.
Mutex.unlock : Mutex.t $\rightarrow$ unit : Déverouille le mutex donné. Les autres fils d'exécution en pause ten-
tant de verouiller le mutex reprennent. Le mutex doit avoir été verrouillé par le fil d'exécution qui appelle
Mutex.unlock.
Module List
List.iter : ('a -> unit) -> 'a list -> unit:iter f [a1; ...; an] applique la fonction f tour à
tour à [a1; ...; an]. Cet application est équivalente à $f a 1 ; f a 2 ; \ldots ; f$ an.
List.map : ('a -> 'b) -> 'a list -> 'b list: map f [a1; ...; an] applique la fonction f à a1,
$\ldots$, an, et construit la liste $[\mathrm{f} \mathrm{a1;} \mathrm{...;} \mathrm{f} \mathrm{an]} \mathrm{avec} \mathrm{les} \mathrm{résultats} \mathrm{renvoyés} \mathrm{par} \mathrm{f}$.
Type enregistrement
type exemple = {mutable a : int; b int}: permet de définir un type enregistrement.
let c = {a = 1; b = 3} permet de définir une variable du type exemple.
c.a permet d'accéder au champ a de c.
c.a<-2 permet de modifier le champ mutable a du type enregistrement c.
Fonction de conversion de type
float_of_int : int -> float: convertit un int en float.
int_of_float : float -> int: convertit un float en int.
V Complexité du problème de la stratégie gagnante au go
Un problème classique qui survient lorsque l'on s'intéresse à des jeux est de se demander quel joueur possède une stratégie gagnante à partir d'une configuration donnée. Ce problème de décision sera étudié ici sous le nom de go généralisé.
Go généralisé
Entrée: Une configuration d'une partie de go géneralisé, c'est-à-dire un goban de dimension
Sortie : Oui s'il existe une stratégie gagnante pour Blanc à partir de cette configuration, non sinon.
Il est possible de montrer que ce problème est NP-dur à partir d'une chaîne de réductions depuis le problème SAT, dont la dernière étape sera montrée dans cette partie.
Q 37. Rappeler la définition de la classe NP, et expliquer ce que signifie être NP-dur et NP-complet. Donner un exemple de problème NP-complet classique autre que SAT et 3SAT, sans prouver son appartenance à cette classe de complexité.
Dans cette partie nous considérons une variante du problème 3SAT, nommée Rectilinear Planar 3SAT, qui est également NP-dur. Tout comme pour 3SAT, les instances de ce problème de décision sont des formules sous forme normale conjonctive avec exactement trois littéraux par clauses, mais désormais chaque clause ne possède que des littéraux positifs, ou que des littéraux négatifs. De plus, la formule en question doit pouvoir se représenter graphiquement de manière planaire rectiligne comme illustré en figure 5, avec toutes les variables alignées horizontalement et les clauses reliées verticalement à leurs variables associées sans aucune intersection. Une telle représentation graphique est également donnée en entrée du problème avec la formule, et n'a donc pas besoin d'être trouvée.
Sortie : Oui s'il existe une stratégie gagnante pour Blanc à partir de cette configuration, non sinon.
Il est possible de montrer que ce problème est NP-dur à partir d'une chaîne de réductions depuis le problème SAT, dont la dernière étape sera montrée dans cette partie.
Q 37. Rappeler la définition de la classe NP, et expliquer ce que signifie être NP-dur et NP-complet. Donner un exemple de problème NP-complet classique autre que SAT et 3SAT, sans prouver son appartenance à cette classe de complexité.
Dans cette partie nous considérons une variante du problème 3SAT, nommée Rectilinear Planar 3SAT, qui est également NP-dur. Tout comme pour 3SAT, les instances de ce problème de décision sont des formules sous forme normale conjonctive avec exactement trois littéraux par clauses, mais désormais chaque clause ne possède que des littéraux positifs, ou que des littéraux négatifs. De plus, la formule en question doit pouvoir se représenter graphiquement de manière planaire rectiligne comme illustré en figure 5, avec toutes les variables alignées horizontalement et les clauses reliées verticalement à leurs variables associées sans aucune intersection. Une telle représentation graphique est également donnée en entrée du problème avec la formule, et n'a donc pas besoin d'être trouvée.
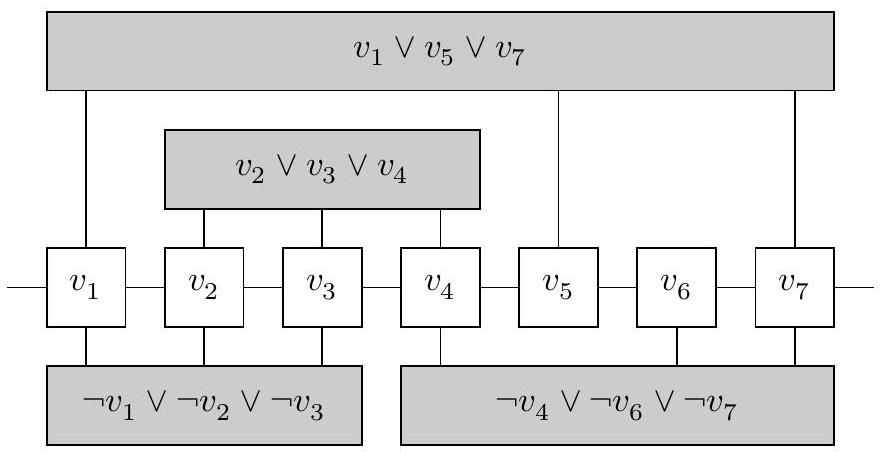
Figure 5 La formule
Soit
Q 38. Expliquer pourquoi si Blanc parvient à relier sa réserve à un gadget (d) de la figure 6, alors Noir ne peut plus capturer les pierres blanches de la réserve.
Ce gadget à atteindre pour sécuriser le groupe de pierres sera nommé des yeux. En tentant à tout prix de relier sa réserve à des yeux, Blanc va progressivement relier sa réserve à des gadgets, qui sont des dispositions
Q 38. Expliquer pourquoi si Blanc parvient à relier sa réserve à un gadget (d) de la figure 6, alors Noir ne peut plus capturer les pierres blanches de la réserve.
Ce gadget à atteindre pour sécuriser le groupe de pierres sera nommé des yeux. En tentant à tout prix de relier sa réserve à des yeux, Blanc va progressivement relier sa réserve à des gadgets, qui sont des dispositions
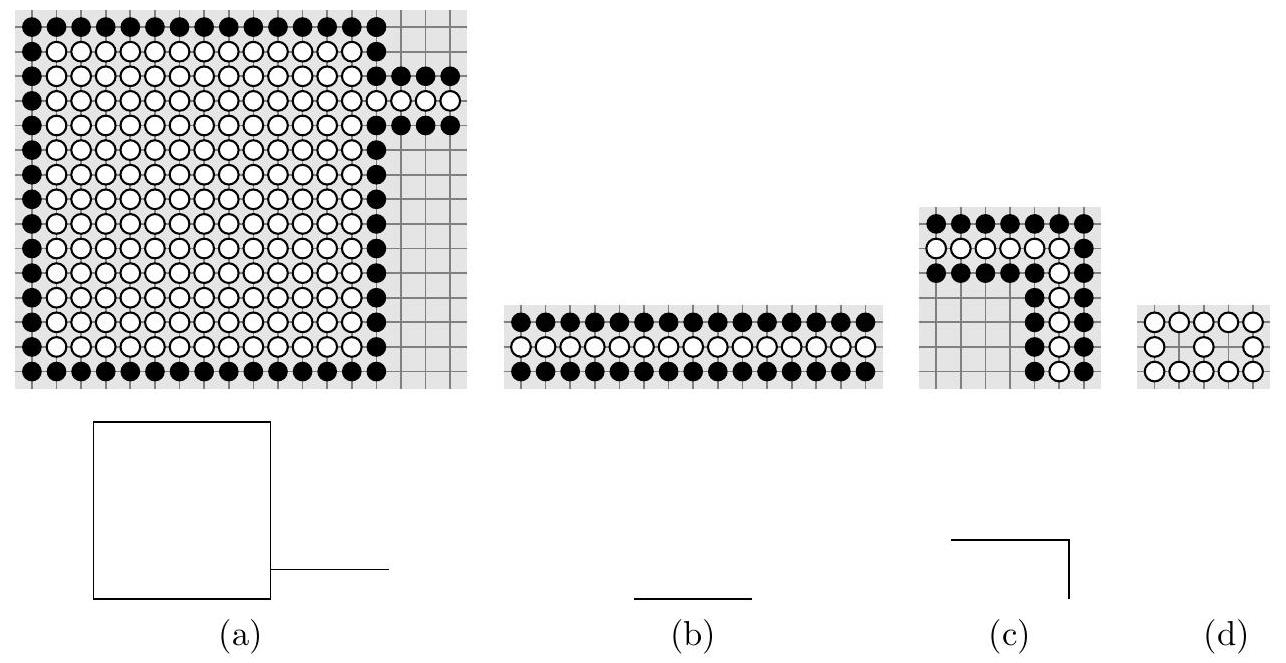
Figure 6 Un exemple de réserve de pierres blanches presque capturée par le joueur noir (a), ainsi que deux sections de tuyaux (b) et (c). Des représentations simplifiées sont données en bas. En (d) une configuration de 13 pierres blanches que Blanc va chercher à relier à sa réserve de pierres blanches pour les sécuriser.
locales de pierres qui vont permettre de simuler un comportement souhaité. Ces gadgets sont construits de sorte que le nombre de libertés du groupe de pierres blanches qui risquent d'être capturées soit toujours de 1 , ou exceptionnellement de 2 dans le gadget (figure 7 (a)) ce qui permet à Blanc de faire un choix ponctuellement. Ce premier gadget (figure 7 (a)) permet de modéliser un choix pour Blanc, qui décidera s'il veut relier le tuyau du haut (supposé relié à la réserve de pierres) au tuyau de gauche ou au tuyau de droite. Nous pourrons supposer que c'est à Blanc de poser la première pierre dans chaque gadget.
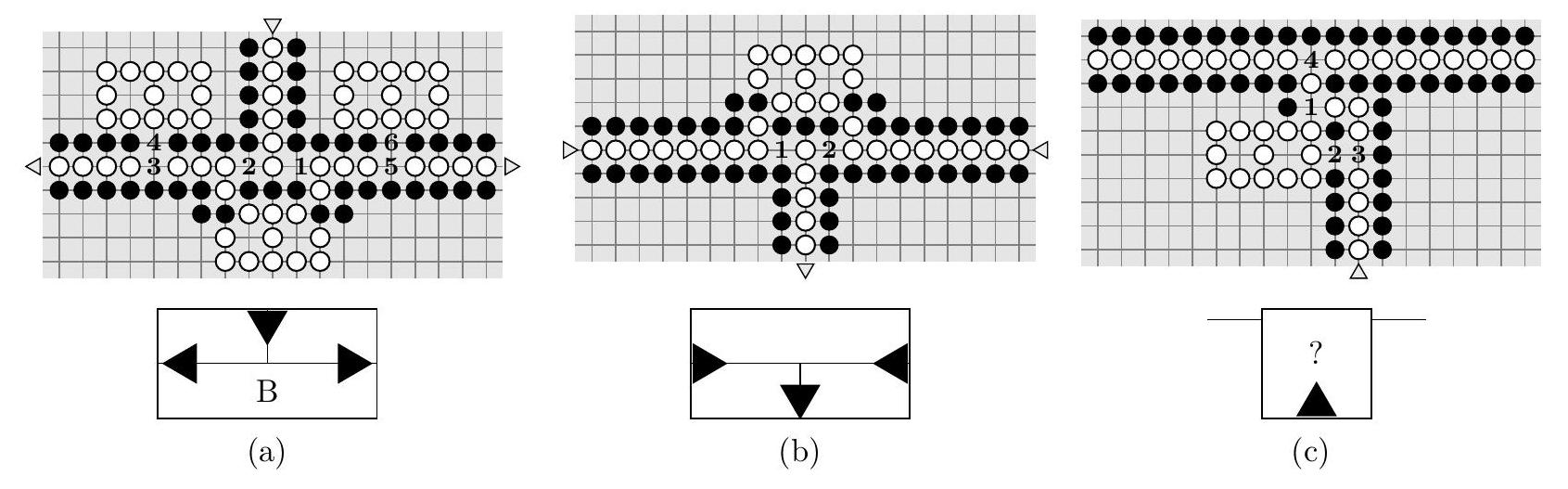
Figure 7 Trois gadgets qui seront utilisés pour la réduction, ainsi que leurs représentations simplifiées associées.
Q 39. Expliciter précisément les deux suites de coups possibles pour le gadget (a), et justifier à l'aide d'un arbre que si Blanc ou Noir s'écarte de l'une de ces deux stratégies, alors l'autre joueur peut arriver à ses fins en au plus deux coups.
Q 40. Décrire des modifications à apporter au gadget (a) pour obtenir un gadget représentant un branchement mais dans lequel c'est Noir qui décide si le tuyau de gauche ou de droite sera relié au tuyau du haut. On rappelle qu'on se place toujours dans le cas où Blanc joue en premier dans les gadgets.
Nous utiliserons, pour ce nouveau gadget, la même représentation simplifiée que le gadget (a) en remplaçant le
Q 41. Que permet de réaliser le gadget (b) ? Justifier.
Q 42. Justifier que le gadget (c) permet, en arrivant par le bas, de tester si le tuyau transversal du haut a déjà été relié à la réserve de pierres blanches par le passé ou pas. On pourra notamment justifier que la partie se décidera sur ce gadget précis, et l'issue en sera uniquement déterminée par le fait que le tuyau transversal du haut ait été préalablement relié à la réserve ou non.
Nous nous intéressons désormais à l'assemblage de ces gadgets pour former un circuit, qui pourra être représenté en utilisant les notations simplifiées. Dans un premier temps, nous allons simuler la valuation de chaque variable par le fait d'avoir relié une section à la réserve ou non.
Q 43. Vérifier que pour chaque variable
Q 44. Vérifier qu'il existe, pour toute valuation des variables, une stratégie permettant à Blanc de relier à la réserve de pierres blanches les sections associées à cette valuation.
Q 40. Décrire des modifications à apporter au gadget (a) pour obtenir un gadget représentant un branchement mais dans lequel c'est Noir qui décide si le tuyau de gauche ou de droite sera relié au tuyau du haut. On rappelle qu'on se place toujours dans le cas où Blanc joue en premier dans les gadgets.
Nous utiliserons, pour ce nouveau gadget, la même représentation simplifiée que le gadget (a) en remplaçant le
Q 41. Que permet de réaliser le gadget (b) ? Justifier.
Q 42. Justifier que le gadget (c) permet, en arrivant par le bas, de tester si le tuyau transversal du haut a déjà été relié à la réserve de pierres blanches par le passé ou pas. On pourra notamment justifier que la partie se décidera sur ce gadget précis, et l'issue en sera uniquement déterminée par le fait que le tuyau transversal du haut ait été préalablement relié à la réserve ou non.
Nous nous intéressons désormais à l'assemblage de ces gadgets pour former un circuit, qui pourra être représenté en utilisant les notations simplifiées. Dans un premier temps, nous allons simuler la valuation de chaque variable par le fait d'avoir relié une section à la réserve ou non.
Q 43. Vérifier que pour chaque variable
Q 44. Vérifier qu'il existe, pour toute valuation des variables, une stratégie permettant à Blanc de relier à la réserve de pierres blanches les sections associées à cette valuation.
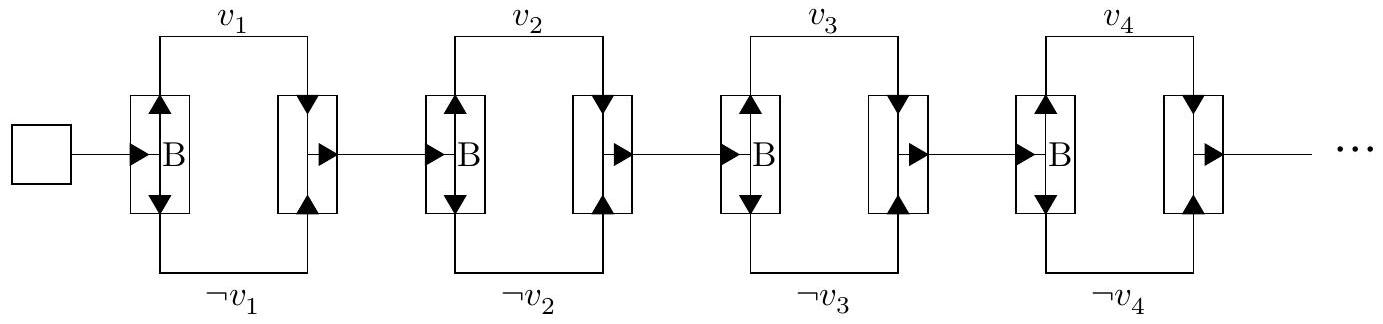
Figure 8 Un circuit représentant le choix d'une valuation, modélisée par le fait de choisir de relier le tuyau du haut ou le tuyau du bas à la réserve pour chaque variable.
Ainsi, Blanc a choisi de relier certaines sections à sa réserve de pierres blanches et la partie est encore en cours. Il reste désormais à déterminer si la valuation choisie par Blanc est un modèle de
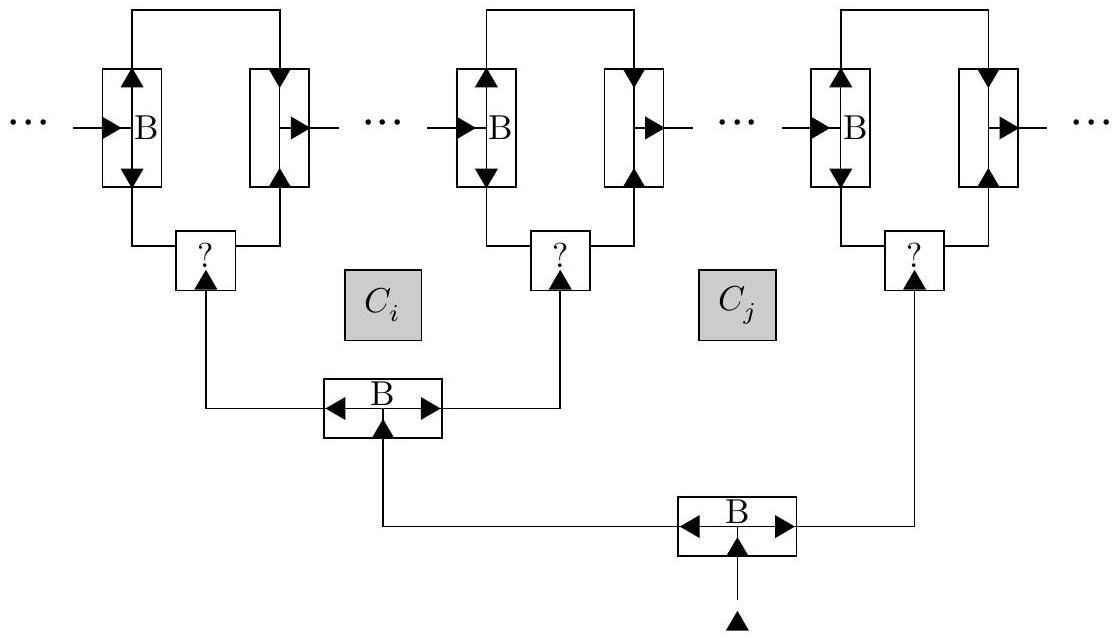
Figure 9 Un gadget permettant à Blanc de vérifier que le littéral de son choix est bien satisfait dans une clause, mais qui bloque le passage à d'autres clauses éventuelles comme
Q 45. Modifier le circuit de vérification de clause proposé, afin que Noir puisse en plus décider d'accéder à une clause intérieure s'il le souhaite, sans en modifier le comportement.
Q 46. En utilisant les questions précédentes, conclure en proposant une réduction complète de Rectilinear Planar 3SAT au jeu de go généralisé.
Q 46. En utilisant les questions précédentes, conclure en proposant une réduction complète de Rectilinear Planar 3SAT au jeu de go généralisé.
