Version interactive avec LaTeX compilé
INFORMATIQUE
Les deux parties sont indépendantes et peuvent être traitées dans un ordre quel conque
Partiel - Algorithmes pour la sélection
Pour
On s'intéresse au problème suivant, appelé problème de la sélection : on a un ensemble E de
Le médian d'un ensemble de n nombres est le
On insiste sur le fait que dans toute la partie I, on considère des tableaux ou listes d'entiers distincts deux à deux.
On s'intéresse au problème suivant, appelé problème de la sélection : on a un ensemble E de
Le médian d'un ensemble de n nombres est le
On insiste sur le fait que dans toute la partie I, on considère des tableaux ou listes d'entiers distincts deux à deux.
I.A - Recherche des deux plus grands éléments
Les éléments de
I.A.1) Soit
a) Donner le nombre de comparaisons nécessaires pour réaliser un tel tournoi.
b) Montrer qu'à l'aide de ce procédé, on peut trouver le maximum et le second plus grand élément des
En fait, on peut montrer (mais cen'est pas demandé) qu'un tel algorithme est optimal.
c) Exemple : appliquer la méthode précédente à l'entrée:
I.A.1) Soit
a) Donner le nombre de comparaisons nécessaires pour réaliser un tel tournoi.
b) Montrer qu'à l'aide de ce procédé, on peut trouver le maximum et le second plus grand élément des
En fait, on peut montrer (mais cen'est pas demandé) qu'un tel algorithme est optimal.
c) Exemple : appliquer la méthode précédente à l'entrée:
d) Comment généraliser cette méthode lorsque
I.A.2) On suppose qu'il existe un algorithme
Filière MP
existe une entrée
a) Si S est un ensemble fini non vide de cardinal
Un tel graphe est dit connexe lorsque pour toute paire de sommets
Montrer que si (
b) Construire une entrée
c) Conclure.
a) Si S est un ensemble fini non vide de cardinal
Un tel graphe est dit connexe lorsque pour toute paire de sommets
Montrer que si (
b) Construire une entrée
c) Conclure.
I.B - Recherche systématique dans un tableau
Les éléments de
I.B.1) On utilise l'algorithme suivant : en supposant
Calculer le nombre de comparaisons effectuées ; quel est son maximum lorsque i varie?
I.B.2) Indiquer un algorithmequi permettrait de résoudrele problème dela sélection pour un i quelconque en
I.B.1) On utilise l'algorithme suivant : en supposant
Calculer le nombre de comparaisons effectuées ; quel est son maximum lorsque i varie?
I.B.2) Indiquer un algorithmequi permettrait de résoudrele problème dela sélection pour un i quelconque en
I.C - Tri rapide dans une liste chaînée
I.C.1) Écrire une fonction (ou une procédure) partition qui, étant donné une liste chaînée d'entiers liste, et un entier pivot (appartenant ou non à la liste) :
- constitue deux listes avant et apres constituées des éléments de liste et telles que :
avant apres, pivot . - retourne les deux listes avant et apres, et le nombre d'éléments nb de la liste avant.
Les candidats rédigeant en Caml devront écrire une fonction de type:
partition : 'a liste 一>'a 一>'a list * 'a list * int = <fun>
partition : 'a liste 一>'a 一>'a list * 'a list * int = <fun>
Ceux rédigeant en Pascal utiliseront la déclaration de type
type
ptrliste=^element;
element=record
entier:integer;
suivant:ptrliste
end;
et ils écriront une procédure dédarée de la façon suivante:
procedure partition(liste:ptrliste; pivot:integer;
var avant,apres:ptrliste; var taille:integer);
I.C.2)
a) Écrire une fonction recherche récursive qui, pour un entier i et une liste d'entiers liste, retourne le i -ème élément de la liste
On utilisera la fonction/procédure partition précédente, en prenant comme pivot le premier élément de la liste. Les candidats ayant choisi Caml écriront une fonction de signature:
recherche : int一>'a list一>'a = <fun>
Ceux ayant choisi Pascal écriront une fonction déclarée:
fonction recherche (liste:ptrliste; i:integer) :integer;
b) J ustifier la terminaison et la correction de la fonction précédente.
c) Donner des indications sur son temps de calcul. On exhibera des «cas limites».
d) Si la distribution des entiers de E est uniforme dans un intervalle, comment choisir l'entier pivot pour réduire au mieux le temps de calcul ?
type
ptrliste=^element;
element=record
entier:integer;
suivant:ptrliste
end;
et ils écriront une procédure dédarée de la façon suivante:
procedure partition(liste:ptrliste; pivot:integer;
var avant,apres:ptrliste; var taille:integer);
I.C.2)
a) Écrire une fonction recherche récursive qui, pour un entier i et une liste d'entiers liste, retourne le i -ème élément de la liste
On utilisera la fonction/procédure partition précédente, en prenant comme pivot le premier élément de la liste. Les candidats ayant choisi Caml écriront une fonction de signature:
recherche : int一>'a list一>'a = <fun>
Ceux ayant choisi Pascal écriront une fonction déclarée:
fonction recherche (liste:ptrliste; i:integer) :integer;
b) J ustifier la terminaison et la correction de la fonction précédente.
c) Donner des indications sur son temps de calcul. On exhibera des «cas limites».
d) Si la distribution des entiers de E est uniforme dans un intervalle, comment choisir l'entier pivot pour réduire au mieux le temps de calcul ?
I.D - Recherche de l'élément médian
L' ensemble des éléments de
On suppose que les deux sous-tableaux
On suppose que les deux sous-tableaux
I.D.1)
a) En utilisant la fonction (supposée donnée) de fusion de deux tableaux triés, donner un algorithme déterminant le médian
b) Évaluer son temps de calcul (on prendra en compte seulement le nombre de comparaisons de deux éléments).
I.D.2) On veut améliorer la recherche précédente en effectuant une recherche dichotomique simultanée sur les deux moitiés du tableau
a) Expliquer (éventuellement à l'aide de schémas) une stratégie à adopter pour déterminer le médian de
b) Donner le code d'une telle fonction. On introduira une fonction récursive de la forme recherche_dicho (
a) En utilisant la fonction (supposée donnée) de fusion de deux tableaux triés, donner un algorithme déterminant le médian
b) Évaluer son temps de calcul (on prendra en compte seulement le nombre de comparaisons de deux éléments).
I.D.2) On veut améliorer la recherche précédente en effectuant une recherche dichotomique simultanée sur les deux moitiés du tableau
a) Expliquer (éventuellement à l'aide de schémas) une stratégie à adopter pour déterminer le médian de
b) Donner le code d'une telle fonction. On introduira une fonction récursive de la forme recherche_dicho (
On rappellequela taille du tableau initial est une puissancede 2.
c) Prouver la validité du programme précédent.
d) Donner un ordre de grandeur de son temps de calcul (on prendra en compte seulement le nombre de comparaisons de deux éléments).
c) Prouver la validité du programme précédent.
d) Donner un ordre de grandeur de son temps de calcul (on prendra en compte seulement le nombre de comparaisons de deux éléments).
I.E - Utilisation d'arbres binaires de recherche
Afin de pouvoir insérer puis rechercher rapidement n'importe quel élément del'ensemble E , on organise les données selon une structure d'arbres binaires de recherche. On utilisera les types suivants:
En Caml :
type arbre = vide | Noeud of Nd
and Nd = {valeur : int; mutable taille : int;
mutable gauche : arbre; mutable droit : arbre};;
En Pascal :
type
type
ptrNoeud=^Noeud;
Noeud = record
valeur, taille : integer;
gauche, droit : ptrNoeud;
end;
Chaque noeud N de la structure d'arbres binaires contient la valeur d'un entier de E , la taille (comptée en nombre de noeuds non vides) de l'arbre de racine N , et des pointeurs vers les deux fils.
I.E.1) Pour tester le fonctionnement du programme, on utilise des nombres entiers engendrés par un processus pseudo-aléatoire, qui sont rangés, l'un à la suite de l'autre, dans l'arbre binaire initial ement vide.
a) On considère la suite de nombres pseudo-aléatoires
b) Même question avec la séquence suivante:
I.E.1) Pour tester le fonctionnement du programme, on utilise des nombres entiers engendrés par un processus pseudo-aléatoire, qui sont rangés, l'un à la suite de l'autre, dans l'arbre binaire initial ement vide.
a) On considère la suite de nombres pseudo-aléatoires
b) Même question avec la séquence suivante:
I.E.2) Écrire une fonction (ou une procédure) insere, récursive, réalisant l'insertion d'un nouvel entier x dans l'arbre binaire a. Cette fonction/procédure devra retourner l'arbre dans lequel on a inséré l'entier x. Dans la mesure du possible, on modifiera les champs de l'arbre donné en paramètre, plutôt que d'en recréer un.
En Caml, la signature de insere sera:
insere : int -> arbre -> arbre = <fun>
En Pascal, la déclaration sera:
procedure insere (x:integer; var a : PtrNoeud)
I.E.3)
a) En supposant que l'arbre est bien équilibré (en un sens que l'on précisera), indiquer un ordre de grandeur du temps d'exécution de la fonction insere en fonction de la taille de l'arbre dans lequel on insère un nouvel élément.
b) Que se passe-t-il si l'arbre n'est pas équilibré ? Citer un cas où cela peut se produire.
I.E.4) Écrire une fonction recherche, récursive, déterminant le
Si on appelle g la tailledu sous-arbregauche, on pourra considérer divers cas suivant la valeur de
En Caml, on aura :
recherche : int
Et en Pascal :
function recherche (k:integer; a:PtrNoeud):integer;
b) Que se passe-t-il si l'arbre n'est pas équilibré ? Citer un cas où cela peut se produire.
I.E.4) Écrire une fonction recherche, récursive, déterminant le
Si on appelle g la tailledu sous-arbregauche, on pourra considérer divers cas suivant la valeur de
En Caml, on aura :
recherche : int
Et en Pascal :
function recherche (k:integer; a:PtrNoeud):integer;
Partie II - Portes Iogiques universelles
Rappels - notations - définitions
-
désigne l'ensemble des booléens: F aux, Vrai avec l'analogie 0 = Faux et Vrai . - Les fonctions logiques sont les applications de
dans , avec . - Les formules logiques sont construites à partir de variables, des connecteurs
, (et), non & (ou exclusif), ainsi éventuellement que des constantes Vrai et Faux. - On rappellequ'à touteformule
construitesur les variables ( ), on associede façon naturel le unefonction .
Réciproquement, siest une application de dans , on sait qu'il existeune formule construite avec les variables ( ) telleque . Il n'y a pas unicité de , mais on peut par exemple imposer à de n'utiliser que les connecteurs et . On dit quel'ensemble{ et } est complet. - Présentons sommairement les circuits logiques : il s'agit d'assemblages orientés de portes logiques élémentaires disposant d'entrées et de sorties.
- Uneporte
est constituéed'entrées et desorties ( ); chaque prend une valeur fonction des . Traditionnellement, les entrées sont repré sentées à gauche et les sorties à droite - On disposedes portes élémentaires suivantes : la porteNON est detype ( 1,1 ), avec
. Les portes OU, ET et XOR sont de type ( 2,1 ), avec (resp. et ).
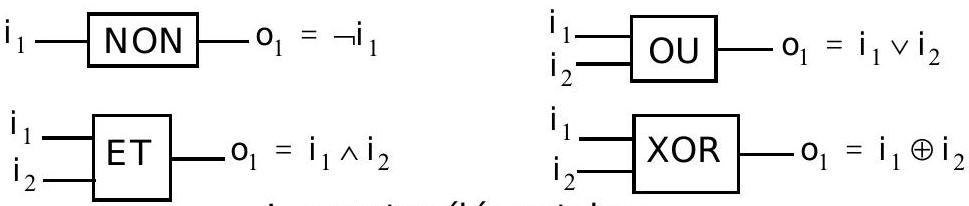
Les portes élémentaires
- Chaque entrée de porte peut constituer une entrée du circuit global, ou bien être reliée à la sortie d'une autre porte, ou encore à une source, qui constitue une porte particulièresans entrée, avec une sortie constante égale à 0 ou 1 .
- Chaque sortie de porte peut constituer une sortie du circuit global, ou bien être reliéeà l'entréed'uneautreporte, ou encoreà un puits, qui est uneporteparticulière sans sortie, avec une entrée: en somme, il s'agit d'une sortie «dont on ne tiendra pas compte».
- L'assemblageest acycliqueau sens où en suivant I'orientation des portes, il n'existe pas de boucle dans le circuit.
- Les duplicateurs sont des portes particulières à une entrée
et deux sorties en et égales à . Ils sont représentés par un cerde plein. Les sources sont repré

Un duplicateur, une source de 1, et un puits. sentées par un carré et les puits par des cercles.
- Un circuit C avec n entrées
et k sorties ( ) calcule de façon naturell e une fonction . Dans l'exemple qui suit, calcule la fonction
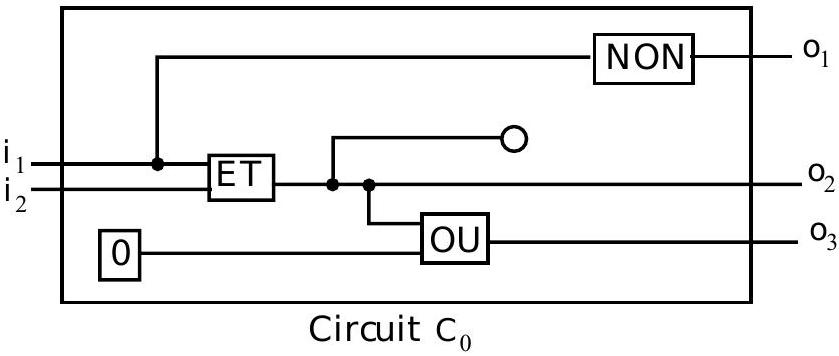
- Deux circuits seront dits équivalents lorsqu'ils cal culent la même fonction.
- Un ensemble E deportes sera dit universel Iorsquetout circuit est équivalent à un autre circuit constitué de portes de E, de duplicateurs, desources et de puits. Lorsque
est réduit à un singleton , on dit que est une porteuniverselle - Enfin, uneporte
detype ( ) sera diteréversiblelorsqu'il existeuneporte de type ( ) telle quel'assemblage constitué dela porte suivie de la porte calculela fonction identitéde . Par exemple, la porteNON est réversible (prendre ).
II.A - Donner deux formules logiques calculant les valeurs respectives deen fonction de et pour le circuit suivant:
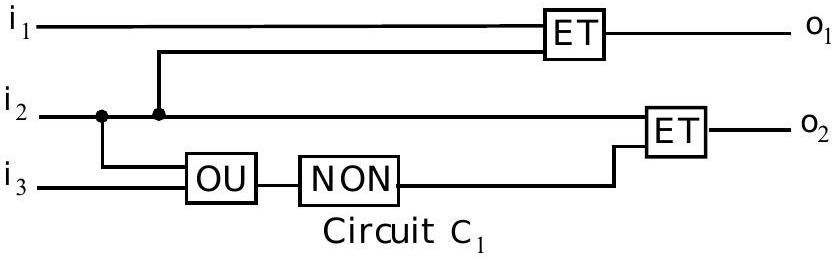
II.B - Ensembles de portes universelles
II.B.1) Construire un circuit logique
On utilisera uniquement des duplicateurs, sources, portes NON, OU et ET.
II.B.2)
a) Montrer que l'ensemble de portes {NON, ET} est universel.
b) Exemple : construire un circuit équivalent à
II.B.3)
a) Montrer que l'ensemble de portes {XOR, OU } est universel.
b) Exemple: construire un circuit équivalent à
II.B.4)
a) Montrer que la porte
b) Construire à partir de
II.B.2)
a) Montrer que l'ensemble de portes {NON, ET} est universel.
b) Exemple : construire un circuit équivalent à
II.B.3)
a) Montrer que l'ensemble de portes {XOR, OU } est universel.
b) Exemple: construire un circuit équivalent à
II.B.4)
a) Montrer que la porte
b) Construire à partir de
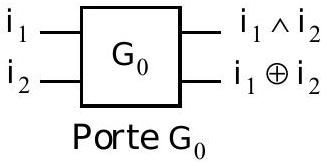
c) Montrer que la porte
II.C - Portes réversibles
II.C.1) Montrer quesi une porte logique (
II.C.2) Quelles sont les portes
II.C.3) Donner deux exemples simples mais non triviaux (i.e. dont les fonctions associées ne sont pas l'identité) de portes ( 2,2 ) réversibles.
II.C.4) Combien existe-t-il de portes
II.C.2) Quelles sont les portes
II.C.3) Donner deux exemples simples mais non triviaux (i.e. dont les fonctions associées ne sont pas l'identité) de portes ( 2,2 ) réversibles.
II.C.4) Combien existe-t-il de portes
II.D - Portes réversibles universelles
II.D.1) On se propose de montrer qu'il n'existe pas de porte (2, 2) réversible et universelle.
Soit G une porte réversible ( 2,2 ).
On note g la fonction de
a) Montrer que
Soit G une porte réversible ( 2,2 ).
On note g la fonction de
a) Montrer que
où + désigne la somme dans
On rappelle quesi
b) Montrer que tout circuit (
c) Conclure.
II.D.2) La porte de Toffoli est la porte logique
a) Montrer que la porte de Toffoli est réversible et universelle.
b) Vérifier que la fonction calculée par T n'est pas affine.
On rappelle quesi
b) Montrer que tout circuit (
c) Conclure.
II.D.2) La porte de Toffoli est la porte logique
a) Montrer que la porte de Toffoli est réversible et universelle.
b) Vérifier que la fonction calculée par T n'est pas affine.
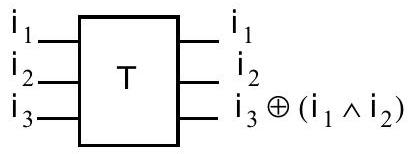
Porte de Toffoli
