Version interactive avec LaTeX compilé
Centrale Option Informatique MP 2020
Un système de vote
Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Un système de vote
Le seul langage de programmation autorisé dans cette épreuve est Caml.
Toutes les fonctions des modules Array et List, ainsi que les fonctions de la librairie standard (celles qui s'écrivent sans nom de module, comme max ou incr ainsi que les opérateurs comme ©) peuvent être librement utilisées. Les candidats ne devront faire appel à aucun autre module.
En Caml, les matrices d'entiers sont représentées par des tableaux de tableaux, c'est-à-dire par le type int array array. L'expression
Toutes les fonctions des modules Array et List, ainsi que les fonctions de la librairie standard (celles qui s'écrivent sans nom de module, comme max ou incr ainsi que les opérateurs comme ©) peuvent être librement utilisées. Les candidats ne devront faire appel à aucun autre module.
En Caml, les matrices d'entiers sont représentées par des tableaux de tableaux, c'est-à-dire par le type int array array. L'expression
- Array.make_matrix : int -> int -> 'a -> 'a array array est telle que Array.make_matrix n p v renvoie une matrice de n lignes et p colonnes dont toutes les cases contiennent la valeur v ;
- Array.length : 'a array -> int est telle que Array.length tab renvoie le nombre d'éléments du tableau tab. Si tab est une matrice, c'est le nombre de lignes de tab;
- min : 'a -> 'a -> 'a renvoie le minimum des deux valeurs en argument ;
- max : 'a -> 'a -> 'a renvoie le maximum des deux valeurs en argument ;
- l'opérateur © concatène deux listes. Par exemple, [2; 0] © [4; 2] renvoie [2; 0; 4; 2].
Dans ce problème, les graphes ont un ensemble de sommets de la forme
I Vote par préférence
Nous considérons une élection, à laquelle se présentent
Les trois types de données suivants sont utilisés pour représenter un vote:
Les trois types de données suivants sont utilisés pour représenter un vote:
- type candidat
int ;; chaque candidat est désigné par un numéro de 0 à ; - type bulletin = candidat list ; ; un bulletin de vote est une liste (ordonnée) de candidats ;
- type urne = bulletin list ;; une urne est un ensemble de bulletins de vote.
Par exemple, s'il y a trois candidats et qu'un électeur préfère le candidat 2 , puis le candidat 0 et enfin considère que le candidat 1 est le moins souhaitable, son bulletin de vote sera
Une fois le vote effectué, on compare les résultats de deux candidats particuliers
Une fois le vote effectué, on compare les résultats de deux candidats particuliers
I.A - Premier exemple
On considère une élection avec trois candidat et trois votants :
Q 1. Écrire une fonction duel : candidat
On peut alors synthétiser le contenu d'une urne u en construisant le graphe de préférence des votants : ses sommets correspondent aux candidats et l'arc du sommet i vers le sommet j est pondéré par la comparaison entre le candidat i et le candidat j, c'est-à-dire la valeur de duel i j u.
La figure 1 donne le graphe de préférence obtenu à partir du vote de l'exemple 1 ainsi que sa matrice d'adjacence
Q 1. Écrire une fonction duel : candidat
On peut alors synthétiser le contenu d'une urne u en construisant le graphe de préférence des votants : ses sommets correspondent aux candidats et l'arc du sommet i vers le sommet j est pondéré par la comparaison entre le candidat i et le candidat j, c'est-à-dire la valeur de duel i j u.
La figure 1 donne le graphe de préférence obtenu à partir du vote de l'exemple 1 ainsi que sa matrice d'adjacence
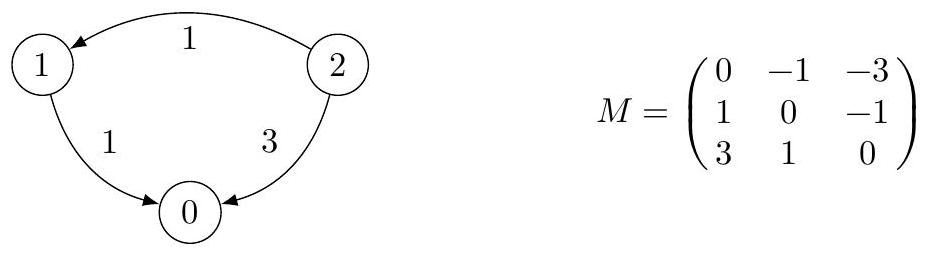
Figure 1
I.B - Deuxième exemple
On considère une élection avec trois candidats et 4 votants :
Q 2. Tracer le graphe de préférence de l'urne (en ne dessinant que les arcs ayant un poids strictement positif) et donner sa matrice d'adjacence.
Q 2. Tracer le graphe de préférence de l'urne (en ne dessinant que les arcs ayant un poids strictement positif) et donner sa matrice d'adjacence.
I.
Q 3. Expliquer pourquoi la matrice d'adjacence d'un graphe de préférence est antisymétrique et pourquoi tous ses coefficients non-diagonaux ont la même parité.
Étant donné une urne
Q 4. Écrire une fonction depouillement : int
Étant donné une urne
Q 4. Écrire une fonction depouillement : int
I.D - Théorème de McGarvey
Le but de cette sous-partie est de démontrer le théorème de McGarvey : «Pour toute matrice antisymétrique à coefficients pairs
Soient
Q 5. Soit
Q 6. On considère deux urnes
Q 7. Démontrer le théorème de McGarvey.
Q 8. Écrire une fonction mcgarvey : int array array
Q 9. Estimer la complexité de la fonction mcgarvey en fonction de
Soient
Q 5. Soit
Q 6. On considère deux urnes
Q 7. Démontrer le théorème de McGarvey.
Q 8. Écrire une fonction mcgarvey : int array array
Q 9. Estimer la complexité de la fonction mcgarvey en fonction de
II Recherche du vainqueur
L'objectif de cette partie est de déterminer le vainqueur, ou les vainqueurs ex aequo, d'un vote par préférence.
II.A - Vainqueur de Condorcet
On appelle vainqueur de Condorcet tout sommet tel que, dans le graphe de préférence, les arcs sortant de ce sommet ont tous un poids positif ou nul. Ainsi, dans le premier exemple de la partie I, le candidat 2 est un vainqueur de Condorcet.
Q 10. Expliquer pourquoi un vainqueur de Condorcet peut être qualifié de «vainqueur» de l'élection.
Q 11. Écrire une fonction condorcet : int array array
Q 12. En se plaçant dans le cas
Q 10. Expliquer pourquoi un vainqueur de Condorcet peut être qualifié de «vainqueur» de l'élection.
Q 11. Écrire une fonction condorcet : int array array
Q 12. En se plaçant dans le cas
II.B - Graphe intermédiaire de Schultze
À la fin du
On appelle poids d'un chemin du graphe de préférence, le minimum des poids des arcs constituant ce chemin. Ainsi, dans le premier exemple de la partie I, le poids du chemin
Le graphe intermédiaire de Schulze est un graphe orienté pondéré complet dont les sommets sont les candidats et dont l'arc du sommet
On appelle poids d'un chemin du graphe de préférence, le minimum des poids des arcs constituant ce chemin. Ainsi, dans le premier exemple de la partie I, le poids du chemin
Le graphe intermédiaire de Schulze est un graphe orienté pondéré complet dont les sommets sont les candidats et dont l'arc du sommet
Q 13. Pour
Q 14. Démontrer que
Q 15. En adaptant l'algorithme de Floyd-Warshall, programmer une fonction intermediaire : int array array
Q 16. Estimez la complexité de la fonction intermediaire en fonction de
Q 17. Serait-il pertinent d'utiliser l'algorithme de Dijkstra au lieu de l'algorithme de Floyd-Warshall ? Argumenter la réponse.
Q 14. Démontrer que
Q 15. En adaptant l'algorithme de Floyd-Warshall, programmer une fonction intermediaire : int array array
Q 16. Estimez la complexité de la fonction intermediaire en fonction de
Q 17. Serait-il pertinent d'utiliser l'algorithme de Dijkstra au lieu de l'algorithme de Floyd-Warshall ? Argumenter la réponse.
II.C - Graphe de préférence de Schulze
Le graphe de préférence de Schulze est défini à partir du graphe intermédiaire de Schulze. Si I est la matrice d'adjacence du graphe intermédiaire de Schulze, alors la matrice d'adjacence
Q 18. Montrer que la matrice d'adjacence d'un graphe de préférence de Schulze est antisymétrique et que tous ses coefficients sont pairs.
Q 19. Écrire une fonction graphe_schulze : int array array
Q 18. Montrer que la matrice d'adjacence d'un graphe de préférence de Schulze est antisymétrique et que tous ses coefficients sont pairs.
Q 19. Écrire une fonction graphe_schulze : int array array
II.D - Vainqueur de Schulze
Un vainqueur de Schulze est un vainqueur de Condorcet dans le graphe de préférence de Schulze.
Q 20. Écrire une fonction schulze : int
Q 21. Estimer la complexité de la fonction schulze en fonction du nombre de candidats
À partir d'un graphe de préférence de Schulze représenté par la matrice
Q 22. Montrer que la relation
Q 20. Écrire une fonction schulze : int
Q 21. Estimer la complexité de la fonction schulze en fonction du nombre de candidats
À partir d'un graphe de préférence de Schulze représenté par la matrice
Q 22. Montrer que la relation
Si
Q 23. Montrer que quelle que soit l'urne non vide considérée, il existe toujours au moins un vainqueur de Schulze.
Q 23. Montrer que quelle que soit l'urne non vide considérée, il existe toujours au moins un vainqueur de Schulze.
III Satisfiabilité d'une formule de logique propositionnelle
Étant donné une variable propositionnelle
On appelle conjonction de clauses, une formule qui est la conjonction entre plusieurs clauses. Par exemple
On appelle interprétation une fonction qui à chaque variable propositionnelle associe une valeur de vérité (vrai ou faux).
On dit qu'une conjonction de clauses est satisfiable s'il existe une interprétation qui la rend vraie, c'est-à-dire qui rend vrai toutes ses clauses, autrement dit qui rend vrai au moins un littéral de chacune de ses clauses.
Le problème SAT consiste à déterminer si une conjonction de clauses est satisfiable :
Entrées : Une conjonction de clauses
Sortie : Un booléen. Vrai si
Q 24. Montrer qu'il est possible de résoudre le problème SAT avec une complexité en
On appelle conjonction de clauses, une formule qui est la conjonction entre plusieurs clauses. Par exemple
On appelle interprétation une fonction qui à chaque variable propositionnelle associe une valeur de vérité (vrai ou faux).
On dit qu'une conjonction de clauses est satisfiable s'il existe une interprétation qui la rend vraie, c'est-à-dire qui rend vrai toutes ses clauses, autrement dit qui rend vrai au moins un littéral de chacune de ses clauses.
Le problème SAT consiste à déterminer si une conjonction de clauses est satisfiable :
Entrées : Une conjonction de clauses
Sortie : Un booléen. Vrai si
Q 24. Montrer qu'il est possible de résoudre le problème SAT avec une complexité en
On considère un vote par préférence pour lequel on a réparti les candidats en trois groupes :
- un candidat
, appelé champion; - un ensemble
de candidats dits automatiques; - un ensemble
de candidats optionnels.
Le problème appelé CONTROL-ADD-ALT consiste à déterminer s'il est possible d'éliminer un certain nombre de candidats optionnels de façon à ce que
Entrées : Le candidat
Sortie: Un booléen. Vrai, s'il est possible de choisir
Sortie: Un booléen. Vrai, s'il est possible de choisir
Pour obtenir le graphe de préférence de l'élection avec l'ensemble de candidats
On appelle instance de CONTROL-ADD-ALT une entrée du problème CONTROL-ADD-ALT et instance de SAT une entrée du problème SAT.
On considère l'algorithme «Transformation d'une formule en élection» qui, étant donné une instance de SAT (c'est-à-dire une conjonction de clauses), construit une instance de CONTROL-ADD-ALT :
On appelle instance de CONTROL-ADD-ALT une entrée du problème CONTROL-ADD-ALT et instance de SAT une entrée du problème SAT.
On considère l'algorithme «Transformation d'une formule en élection» qui, étant donné une instance de SAT (c'est-à-dire une conjonction de clauses), construit une instance de CONTROL-ADD-ALT :
Entrées : Une conjonction de clauses
Sortie : Un candidat
pour tout
fin pour
Créer un nouveau candidat
Créer un graphe
pour tout
Créer un nouveau candidat
Ajouter à
fin pour
pour tout
Créer un nouveau candidat
Créer un nouveau candidat
Ajouter à
fin pour
pour tout couple
Ajouter à
fin pour
Compléter le graphe
renvoyer
Q 25. Donner le graphe de préférence créé à partir de la formule
Q 26. Montrer que si on peut choisir
Q 27. Justifier que
On dit qu'un algorithme est en temps polynomial en un paramètre
Conjecture. Il n'existe pas d'algorithme en temps polynomial en nombre de littéraux de l'entrée qui résout SAT.
Q 28. Montrer que, si la conjecture précédente est vraie, alors il n'existe pas d'algorithme en temps polynomial en nombre de candidats qui résout CONTROL-ADD-ALT.
Sortie : Un candidat
pour tout
fin pour
Créer un nouveau candidat
Créer un graphe
pour tout
Créer un nouveau candidat
Ajouter à
fin pour
pour tout
Créer un nouveau candidat
Créer un nouveau candidat
Ajouter à
fin pour
pour tout couple
Ajouter à
fin pour
Compléter le graphe
renvoyer
Q 25. Donner le graphe de préférence créé à partir de la formule
Q 26. Montrer que si on peut choisir
Q 27. Justifier que
On dit qu'un algorithme est en temps polynomial en un paramètre
Conjecture. Il n'existe pas d'algorithme en temps polynomial en nombre de littéraux de l'entrée qui résout SAT.
Q 28. Montrer que, si la conjecture précédente est vraie, alors il n'existe pas d'algorithme en temps polynomial en nombre de candidats qui résout CONTROL-ADD-ALT.
