Version interactive avec LaTeX compilé

Centrale Option Informatique MP 2023

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

Centrale MP Centrale 2023 MP Info Info 2023

2025_08_29_81da5cf7f41f43d14325g

Ce sujet comporte quatre parties.
La partie I est totalement indépendante des suivantes et étudie des transformations sur des langages.
Les autres parties s'intéressent à des structures de données représentant des ensembles d'entiers naturels

contenus dans

, «denses » au sens où

est du même ordre de grandeur que

. On cherche à optimiser le temps d'exécution des opérations de test d'appartenance, d'insertion ou de suppression d'un élément, de calcul du minimum, de calcul de l'élément de

immédiatement supérieur à

(qu'on appellera successeur de

dans

, même si

n'appartient pas à

) ou d'opérations ensemblistes telles que l'union.
Dans la partie II, on étudie des structures ordinaires dont on identifie le défaut. Dans la partie III, on étudie une structure simple d'arbre complet modélisant des parties de

et dans la partie IV, on implémente des arbres de van Emde Boas qui, sur des parties

, donnent des opérations en temps quasi-constant.

I Langages et automates

Dans cette partie, on s'intéresse à des transformations sur des langages définis sur un alphabet à deux lettres

. On note

la réunion de deux langages

le mot vide (ou le langage réduit au mot vide, suivant le contexte). Les automates considérés sont des quadruplets (

) où

est l'ensemble des états de l'automate,

l'ensemble de ses états initiaux,

l'ensemble de ses états finals et

l'ensemble de ses transitions.

Soit

deux langages. On définit le langage noté

par

Q1. Déterminer les langages suivants :

Q 2. Soit

trois langages. Exprimer à l'aide de

les langages suivants :

On ne justifiera que la formule portant sur l'étoile de Kleene.
Q 3. Montrer que si

sont deux langages réguliers,

est régulier.
Q 4. Donner l'exemple d'un langage régulier

et d'un langage non régulier

tel que

soit régulier. On justifiera en détail que le langage

proposé n'est pas régulier.
Q 5. À l'aide d'automates reconnaissant des langages réguliers

et d'

-transitions, construire un automate à

-transitions reconnaissant

. On expliquera la construction puis on formalisera l'automate correspondant. Il est inutile de justifier qu'il convient.
On définit sur

l'application

par:

On note alors pour tout langage

le langage défini par :

Q 6. Pour chacun des langages

suivants, déterminer

puis

Q 7. Soit

un langage régulier et

un automate le reconnaissant. Pour

, on note

l'ensemble des mots qui étiquettent un chemin de l'état

à l'état

dans

. Exprimer

à l'aide de langages

et du langage

. On portera une attention particulière au cas du mot vide et on justifiera la formule proposée.

Q 8. Montrer que si

est régulier,

est régulier.
Q 9. Montrer que si

n'est pas régulier,

ne l'est pas non plus.
Q 10. Montrer que si

est régulier,

est régulier. Étudier la réciproque.

II Représentations classiques d'ensembles

Dans cette partie, on implémente des ensembles par des structures connues. On note

le cardinal d'un ensemble

II.A - Avec une liste triée

Q 11. Dans cette question uniquement, on implémente un ensemble d'entiers positifs par la liste de ses éléments, rangés dans l'ordre croissant. Écrire une fonction succ_list de signature int list

int

int prenant en arguments une liste d'entiers distincts dans l'ordre croissant et un entier

et renvoyant le successeur de

dans la liste, c'est-à-dire le plus petit entier strictement supérieur à

de la liste ( -1 si cela n'existe pas). Donner sa complexité dans le pire cas.

II.B - Avec un vecteur trié

Soit

un entier naturel strictement positif, fixé pour toute cette partie. On choisit de représenter un ensemble d'entiers

de cardinal

par un tableau t de taille

dont la case d'indice 0 indique le nombre

d'éléments de

et les cases d'indices 1 à

contiennent les éléments de

rangés dans l'ordre croissant, les autres cases étant non significatives. Par exemple, le tableau [|3;2;5;7;9;1;14|] représente l'ensemble à 3 éléments

.
Q 12. Pour une telle implémentation d'un ensemble

, décrire brièvement des méthodes permettant de réaliser chacune des opérations ci-dessous (on ne demande pas d'écrire des programmes) et donner leurs complexités dans le pire cas :

déterminer le maximum de ;
tester l'appartenance d'un élément à ;
ajouter un élément dans (on suppose la taille du tableau suffisante et que n'appartient pas à ).

Q 13. Par une méthode dichotomique, écrire une fonction succ_vect de signature int array

int

int prenant en arguments un tableau t codant un ensemble

comme ci-dessus et un entier x et renvoyant le successeur de x dans

( -1 si cela n'existe pas).
Q 14. Calculer la complexité dans le pire cas de la fonction succ_vect en fonction de

.
Q 15. Écrire une fonction union_vect de signature int array

int array

int array prenant en arguments deux tableaux

, de taille

, codant deux ensembles

et renvoyant le tableau correspondant à

. On supposera que

II.C - Avec un arbre binaire de recherche

On choisit maintenant de représenter un ensemble d'entiers à l'aide d'un arbre binaire de recherche, les nœuds étant étiquetés par les éléments de

. On définit le type
type abr

Nil | Noeud of int

abr

abr
Pour un tel arbre, pour tout nœud

, les étiquettes de tous les nœuds du sous-arbre gauche de

, s'il y en a, doivent être inférieures à l'étiquette de

et les étiquettes de tous les nœuds du sous-arbre droit de

, s'il y en a, doivent être supérieures à l'étiquette de

.
Par exemple, on peut représenter l'ensemble

par l'arbre figure 1.

Figure 1 Un arbre binaire de recherche pour l'ensemble

Q 16. Écrire une fonction min_abr de signature abr

int prenant en argument un arbre binaire de recherche représentant un ensemble

et renvoyant son étiquette minimale ( -1 si l'ensemble est vide).
Q 17. Écrire une fonction récursive partitionne_abr de signature abr -> int -> (bool * abr * abr) prenant en arguments un arbre binaire de recherche représentant un ensemble

et un entier

et renvoyant un
triplet (b, ag, ad) où b vaut true si

appartient à

et false sinon, ag est un arbre binaire de recherche codant les éléments de

strictement plus petits que

et ad un arbre binaire de recherche codant les éléments de

strictement plus grands que

.
Q 18. Écrire une fonction insertion_abr de signature abr

int

abr prenant en arguments un arbre binaire de recherche représentant un ensemble

et un entier

et renvoyant un arbre binaire de recherche associé à l'ensemble

et de racine étiquetée par

. Calculer sa complexité dans le pire cas en fonction de l'arbre reçu puis en fonction de

.
Q 19. Écrire une fonction union_abr de signature abr

abr

abr prenant en arguments deux arbres binaires de recherche représentant deux ensembles

et renvoyant un arbre binaire de recherche associé à l'ensemble

. On expliquera brièvement la méthode choisie.

III Représentation par arbres binaires complets

On considère dans cette partie des arbres binaires complets dont les nœuds sont étiquetés par des booléens. On rappelle que la profondeur d'un nœud est égale à la longueur du chemin reliant la racine à ce nœud et la hauteur d'un arbre est la plus grande profondeur de ses feuilles (la racine est donc à la profondeur 0 ). Les nœuds seront numérotés à partir de la racine qui porte le numéro 1 dans l'ordre d'un parcours en largeur (de gauche à droite à chaque profondeur).

Figure 2 Numérotation des nœuds

Q 20. Dans un arbre binaire complet de hauteur

, quel numéro peut avoir un nœud à la profondeur

? Combien le sous-arbre dont la racine a le numéro

a-t-il de feuilles ?
Q 21. Dans un arbre binaire complet de hauteur

, pour le nœud numéro

, donner, en les justifiant, les numéros de son fils gauche, de son fils droit et de son père.
Informatiquement, un tel arbre complet de hauteur

sera implémenté par un tableau de booléens de taille

, la case d'indice

contenant l'étiquette du nœud numéroté

. La case d'indice 0 n'est pas utilisée. On notera que dans tous les programmes de cette partie, on peut avoir accès à la valeur

via la taille du tableau.
Soit

. On choisit de coder un ensemble

par un arbre binaire complet de hauteur

selon les règles suivantes:

chaque feuille numérotée est étiquetée par true si et seulement si ;
chaque nœud interne est étiqueté par le «ou logique» des étiquettes de ses deux fils.
let ensemble = bool array ;;

Par exemple, l'ensemble

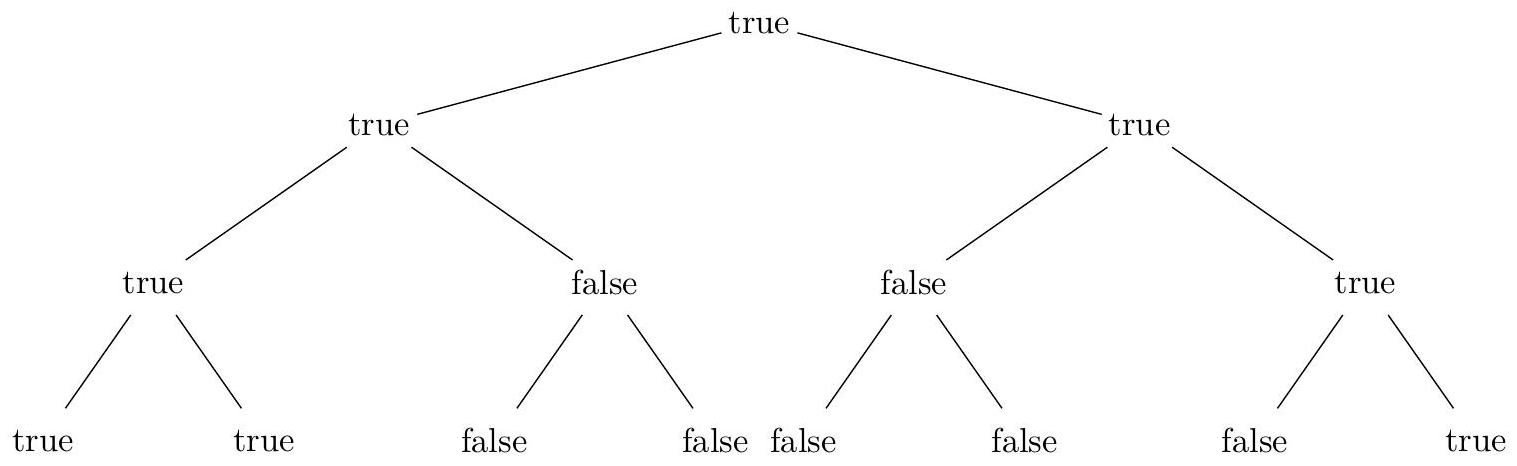
est représenté par l'arbre représenté figure 3.

Figure 3 Arbre associé à l'ensemble

pour

Q 22. Écrire une fonction appartient de signature ensemble -> int -> bool qui détermine si un entier quelconque appartient ou non à un ensemble donné. Calculer sa complexité.

Q 23. Écrire une fonction fabrique de signature int list

int

ensemble qui prend en arguments une liste d'entiers positifs distincts

et une valeur pour

et renvoie l'arbre associé à l'ensemble

dont les éléments sont ceux de la liste. On supposera que tous les éléments de

appartiennent à

. Cette fonction devra s'exécuter en

.
Q 24. Écrire une fonction insere de signature ensemble

int

unit qui ajoute un entier

à un ensemble

. On suppose

compatible avec la valeur de

associée à

. Cette fonction devra s'exécuter en

dans le meilleur cas.
Q 25. Écrire une fonction supprime de signature ensemble

int

unit qui retire un entier

d'un ensemble

. On suppose

compatible avec la valeur de

associée à

. Calculer la complexité de cette fonction dans le pire cas.
Q 26. Écrire une fonction minlocal de signature ensemble

int

int qui cherche l'élément de

minimal parmi ceux codés dans le sous-arbre de racine numérotée

dans l'arbre associé à

. Si un tel élément n'existe pas, cette fonction devra renvoyer -1 . Calculer la complexité de cette fonction en fonction de

.
On veut maintenant écrire une fonction qui calcule le successeur d'un entier

dans un ensemble

pour une telle structure. On propose l'algorithme suivant, pour

on part de la case numéro codant l'entier dans ;
tant que n'est pas le nœud le plus à droite à sa profondeur et que la case vaut false, on remplace par son père ;
on renvoie l'élément minimum du sous-arbre de racine ou -1 si était totalement à droite.

Q 27. Prouver l'algorithme décrit ci-dessus.
Q 28. Écrire une fonction successeur de signature ensemble

int

int prenant en arguments l'ensemble

et un entier

positif et renvoyant son successeur dans

( -1 si cela n'existe pas).
Q 29. Montrer que si

admet bien un successeur dans

, il existe une constante

indépendante de

telle que la complexité de successeur e x soit majorée par

. On admet que le même type de justification montre que si

est le maximum de

, la complexité de successeur e x est majorée par

.
Q 30. En utilisant la fonction successeur, écrire une fonction cardinal de signature ensemble

int prenant en argument un ensemble et renvoyant son cardinal.
Q 31. Déterminer la complexité de la fonction cardinal en fonction de

. On rappelle que la fonction

est concave.
Q 32. Quels sont les intérêts et inconvénients d'une telle structure ? Dans quels cas peut-elle s'avérer plus intéressante que des structures connues ?

IV Arbres de van Emde Boas

Soit

un entier positif et

. On supposera que tous les entiers manipulés restent représentables par la structure d'entier OCaml ordinaire. On considère le type de structure suivant (appelé arbre veb par suite) implémentant un ensemble

d'entiers positifs strictement inférieurs à

:
type veb

mutable mini : int; mutable maxi : int; table : veb array};;
Les champs mutables d'un arbre veb sont modifiables : par exemple, pour un arbre veb noté v, v.mini <- 1 change la valeur du champ v.mini.
Le codage d'un ensemble

par un arbre veb dit d'ordre

suit les règles suivantes :

Les champs mini et maxi représentent toujours la valeur minimale et maximale de . Ils sont mis arbitrairement à -1 si l'ensemble est vide.
Si , i.e. si l'arbre doit coder une partie de , le champ table est un tableau vide (i.e. [।|]), les champs mini et maxi suffisant à coder . On veillera à ce que les fonctions demandées traitent correctement ce cas particulier.
Pour , on note (où désigne le minimum de ). On décompose en ensembles définis par

le champ table est alors un tableau de

arbres veb d'ordre

pour , l'arbre veb stocké dans la case table. (k) code l'ensemble ;
l'arbre veb stocké dans la case table. code l'ensemble .

Par exemple, considérons l'arbre veb ex codant l'ensemble

avec

i.e.

. On a

puisque

et donc les cinq cases du tableau ex. table correspondent respectivement aux ensembles

On obtient la structure représentée figure 4.

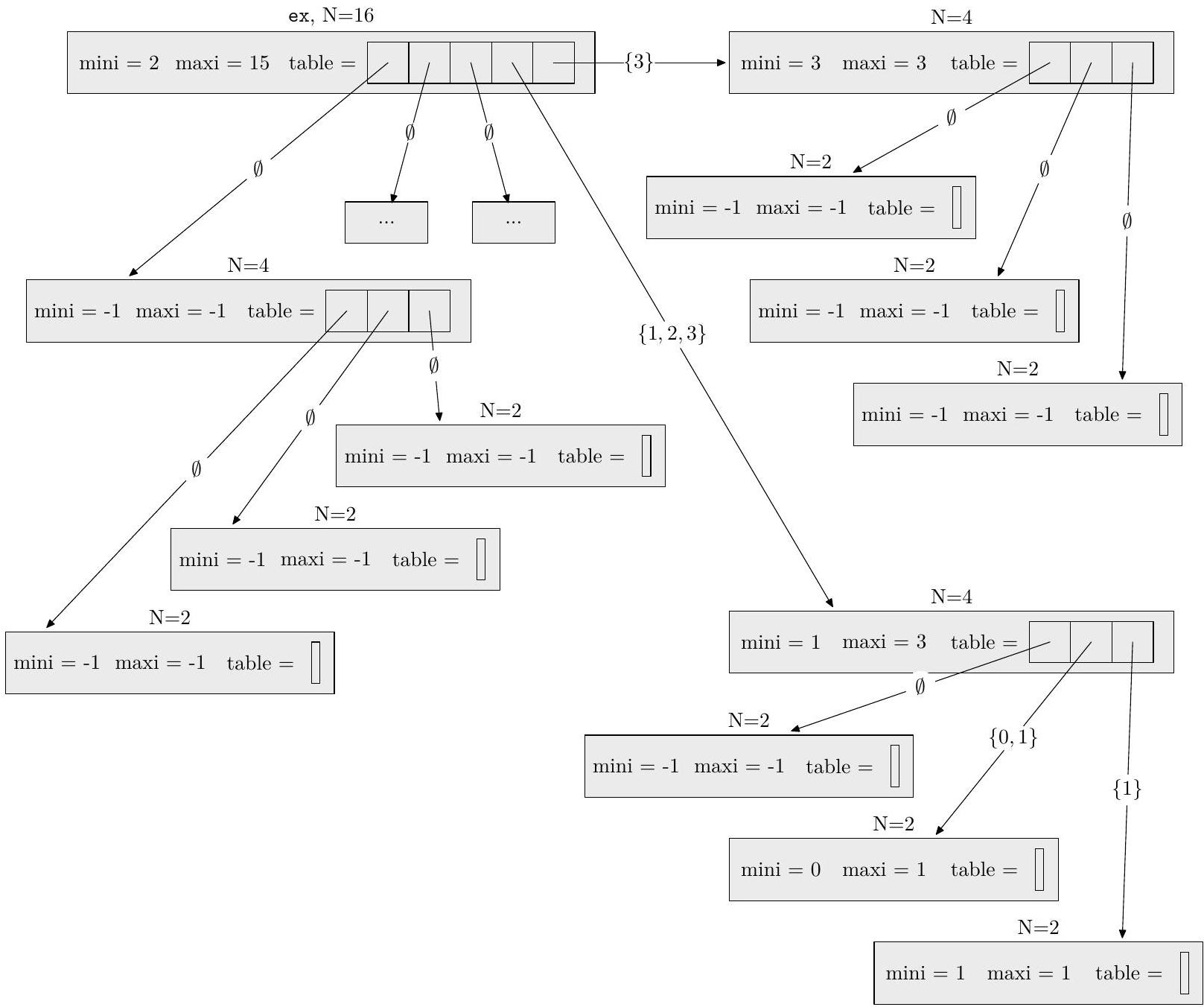
Figure 4 L'arbre veb ex associé à l'ensemble

avec

Q 33. On veut coder l'ensemble

par un arbre veb d'ordre

, noté ex_veb. Indiquer quel ensemble code chaque arbre veb stocké dans ex_veb.table puis préciser ex_veb.table. (3).
Q 34. Écrire une fonction creer_veb de signature int

veb prenant en argument un entier

et créant un arbre veb d'ordre

implémentant l'ensemble vide.
Q 35. Résoudre en fonction de

la récurrence

dans le cas où

.
Q 36. Écrire une fonction appartient_veb de signature veb

int

bool qui teste l'appartenance d'un entier

quelconque à un ensemble

codé par un arbre veb. Calculer sa complexité dans le pire cas.
Q 37. Écrire une fonction successeur_veb de signature veb

int

int qui calcule le successeur d'un entier

quelconque dans

( -1 s'il n'y en a pas). Calculer sa complexité dans le pire cas.
Q 38. Écrire une fonction insertion_veb de signature veb

int

unit qui insère un entier

dans un arbre veb. On suppose que

. Cette fonction devra avoir une complexité en

.
Q 39. Soit

la totalité de l'espace mémoire nécessaire pour stocker un ensemble par un arbre veb d'ordre

avec

. Donner la relation de récurrence vérifiée par

puis déterminer l'ordre de grandeur de