Version interactive avec LaTeX compilé
Quelques aspects de la physique du viseur de casque TopOwl
Le viseur de casque TopOwl

Figure 1 Pilote portant un casque TopOwl
Ce viseur de casque a pour but de permettre au pilote de lire un certain nombre d'informations relatives au vol (rôle de «tableau de bord»), tout en étant capable d'observer le «paysage»; les informations sont projetées sur sa visière et accompagnent donc les mouvements de la tête du pilote.
Ce problème, constitué de trois parties indépendantes, aborde deux aspects majeurs du fonctionnement du viseur de casque TopOwl
Ce problème, constitué de trois parties indépendantes, aborde deux aspects majeurs du fonctionnement du viseur de casque TopOwl
I Affichage par tubes cathodiques
La première technique encore employée aujourd'hui pour l'affichage des informations relatives au vol est à base de deux tubes cathodiques (cylindres de longueur 10 cm , de diamètre 2 cm environ) disposés sur les côtés gauche et droit du casque. Les tubes cathodiques délivrent une «image» lumineuse, représentant l'affichage des informations. Cette image est ensuite transportée et projetée sur la visière du casque par un dispositif à prismes et miroirs non étudié ici. Un tube cathodique est, en première approximation, un dispositif constitué d'un canon à électrons produisant un faisceau d'électrons, d'un dispositif de déviation du faisceau électronique et d'un écran fluorescent émettant de la lumière à l'endroit où il est frappé par le faisceau d'électrons. En réalité, il faut aussi prévoir un dispositif de focalisation du faisceau, ce qu'on appelle une «lentille électrostatique ». On n'étudiera pas ici ce dispositif.
Nous allons étudier ici les principaux éléments d'un modèle simplifié de tube cathodique.
Nous allons étudier ici les principaux éléments d'un modèle simplifié de tube cathodique.
I.A - Canon à électrons
Le canon à électrons est constitué d'une électrode métallique plane (appelée cathode) chauffée et émettant des électrons par effet thermoélectronique. La cathode est au potentiel 0 V . Les électrons sont émis avec une vitesse négligeable et sont ensuite accélérés sous l'effet d'un champ électrique, créé par la différence de potentiel régnant entre la cathode émettrice et une seconde électrode métallique plane (l'anode), parallèle à la cathode, portée au potentiel
de révolution
I.A.1) Exprimer la vitesse
I.A.2) Calculer
de révolution
I.A.1) Exprimer la vitesse
I.A.2) Calculer
I.B - Dispositif de déviation du faisceau
Le faisceau sortant du canon à électrons est supposé homocinétique (de vitesse
I.B.1) Écrire et projeter l'équation du mouvement d'un électron traversant cette zone.
I.B.2) On suppose que les composantes de vitesse
I.B.3) Entre la sortie de la zone de déviation et l'écran, l'électron traverse une zone de longueur
I.B.4) On cherche dans cette question à évaluer la qualité de l'approximation faite en I.B.2.
a) En intégrant directement et sans approximation les équations différentielles régissant les composantes
b) Toujours sans faire d'approximation, montrer que
c) En déduire que le temps de vol
d) Déduire de ce qui précède l'expression et la valeur numérique de la composante
I.B.1) Écrire et projeter l'équation du mouvement d'un électron traversant cette zone.
I.B.2) On suppose que les composantes de vitesse
I.B.3) Entre la sortie de la zone de déviation et l'écran, l'électron traverse une zone de longueur
I.B.4) On cherche dans cette question à évaluer la qualité de l'approximation faite en I.B.2.
a) En intégrant directement et sans approximation les équations différentielles régissant les composantes
b) Toujours sans faire d'approximation, montrer que
c) En déduire que le temps de vol
d) Déduire de ce qui précède l'expression et la valeur numérique de la composante
II Affichage par LCD (liquid crystal display)
Ces afficheurs tendent à remplacer les tubes cathodiques. Le temps de latence de l'afficheur à cristaux liquides du viseur de casque est de l'ordre de 5 ms , inférieur au temps de persistance rétinienne (lequel est de l'ordre de 120 ms ). Nous allons en étudier le principe de fonctionnement.
Les cristaux liquides sont des matériaux présentant des propriétés physiques intermédiaires entre les phases solides et liquides. Ils sont en général constitués de longues macromolécules organiques (que l'on peut assimiler à des bâtonnets).
Les cristaux liquides sont des matériaux présentant des propriétés physiques intermédiaires entre les phases solides et liquides. Ils sont en général constitués de longues macromolécules organiques (que l'on peut assimiler à des bâtonnets).
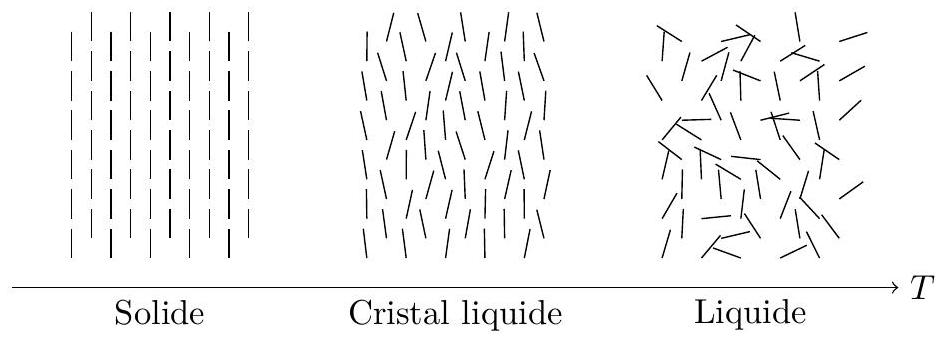
Figure 2
Une conséquence immédiate est l'anisotropie des propriétés physiques des cristaux liquides, et notamment de leurs propriétés optiques. Cette anisotropie est généralement plus élevée que dans les cristaux. L'existence d'un ordre liquide garantit par ailleurs le caractère fluide des cristaux liquides et dans une certaine mesure le basculement facile des axes des molécules en bâtonnets. Cette propriété est essentielle pour l'application aux affichages.
Il existe plusieurs phases cristal liquide, présentant différents degrés et types d'ordre. Nous ne considérerons que les cristaux liquides dits «nématiques», qui présentent un ordre d'orientation mais non de position : les bâtonnets ont tendance à s'aligner parallèlement les uns aux autres, mais sont libres de glisser les uns sur les autres. La direction moyenne locale des axes moléculaires est alors repérée par un vecteur unitaire
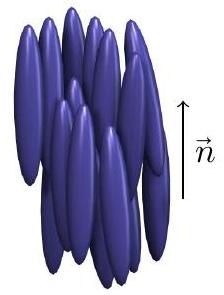
Figure 3 Molécules de cristal liquide orientées
II.A - Expérience préliminaire
On considère un cristal liquide contenu dans un prisme creux d'angle au sommet
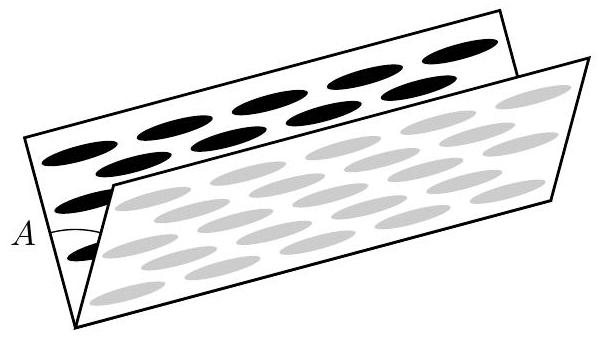
Figure 4 Molécules ancrées sur les faces du prisme
On envoie sur le prisme un faisceau laser non polarisé, perpendiculairement à l'arête du prisme et arrivant sur la face d'entrée du prisme sous incidence normale. On récupère en sortie du prisme deux faisceaux polarisés rectilignement : l'un, polarisé selon le directeur
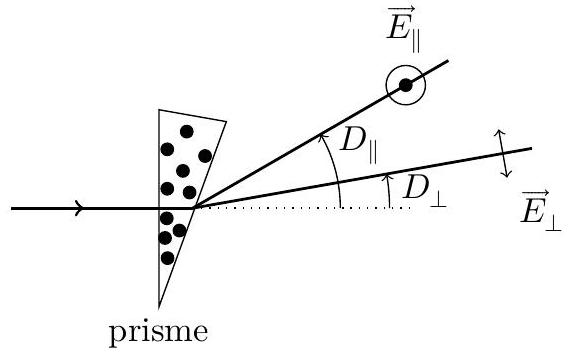
Figure 5
II.A.1) Expliquer comment et avec quel matériel vous procéderiez pour déterminer les états de polarisation des deux ondes émergentes.
II.A.2) L'expérience décrite ci-dessus suggère que les deux composantes du champ électrique
II.A.2) L'expérience décrite ci-dessus suggère que les deux composantes du champ électrique
II.B - Cellule d'affichage à nématique torsadé
La figure 6 représente une cellule d'affichage à nématique torsadé, correspondant à un pixel. Le schéma (a) montre que les directions d'ancrage des molécules en bâtonnets sur la face d'entrée de la cellule (en haut) et sur la face de sortie (en bas), forment un angle de
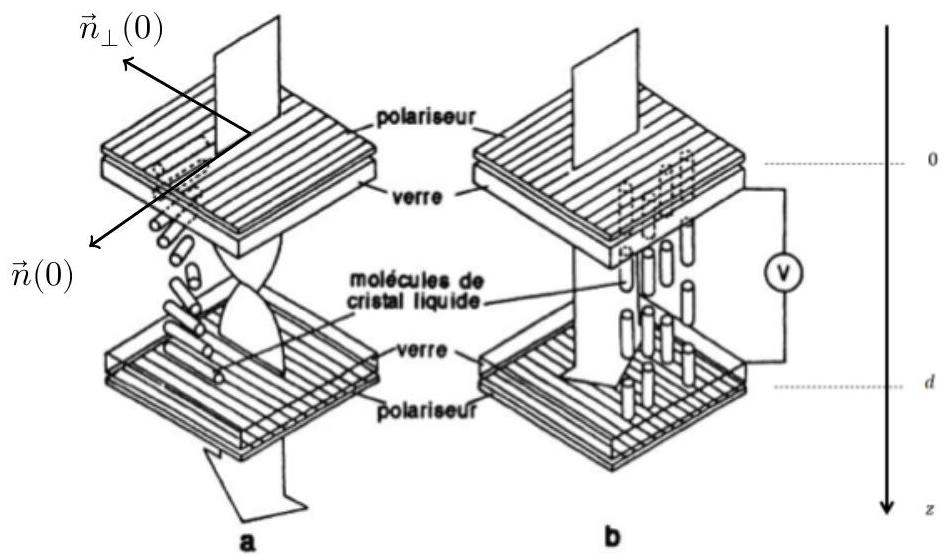
Figure 6 Cellule d'affichage à nématique torsadé
Le schéma (b) correspond au cas où la cellule est soumise à une tension
L'objet de cette partie est de comprendre le fonctionnement de cette cellule et, notamment, l'interaction entre les molécules du nématique et la polarisation de l'onde lumineuse.
II.B.1) On s'intéresse dans un premier temps au cas où la cellule est sous tension (cas de la figure 6b). L'onde incidente est plane, progressive, monochromatique (de pulsation
a) On suppose qu'on peut assimiler les molécules de nématique à des dipôles électrostatiques dont le moment dipolaire
b) Dans cette configuration, lequel des deux indices de réfraction
L'objet de cette partie est de comprendre le fonctionnement de cette cellule et, notamment, l'interaction entre les molécules du nématique et la polarisation de l'onde lumineuse.
II.B.1) On s'intéresse dans un premier temps au cas où la cellule est sous tension (cas de la figure 6b). L'onde incidente est plane, progressive, monochromatique (de pulsation
a) On suppose qu'on peut assimiler les molécules de nématique à des dipôles électrostatiques dont le moment dipolaire
b) Dans cette configuration, lequel des deux indices de réfraction
II.B.2) Propagation d'une onde électromagnétique polarisée rectilignement dans un nématique torsadé
On s'intéresse maintenant au cas où la cellule n'est soumise à aucune tension (cas de la figure 6a). On modélise le milieu torsadé par un empilement de couches
a) Exprimer
On introduit un vecteur unitaire
a) Exprimer
On introduit un vecteur unitaire
b) Soit
Par définition,
c) Exprimer le champ électrique
d) En supposant
d) En supposant
f) On définit l'approximation de Mauguin par la condition :
g) En s'aidant des résultats de la question II.A.2, justifier que, dans l'approximation de Maugin, le champ électrique est de la forme
h) Compte tenu de la condition aux limites en
i) Quelle épaisseur minimale doit-on donner à la cellule sachant que
i) Quelle épaisseur minimale doit-on donner à la cellule sachant que
II.B.3) Afficheur extra-plat
Les considérations développées ci-dessus montrent que la cellule d'affichage ne remplit correctement son office que si la condition de Mauguin
Dorénavant, on ne suppose plus la condition de Mauguin vérifiée :
a) Compte tenu de la condition aux limites en
Dorénavant, on ne suppose plus la condition de Mauguin vérifiée :
a) Compte tenu de la condition aux limites en
b) À l'aide d'une équation du système établi en II.B.2d, on peut montrer sans difficulté (ce qui n'est pas demandé) que:
On dispose ici le polariseur de sortie parallèlement au polariseur d'entrée.
Montrer que le rapport
Montrer que le rapport
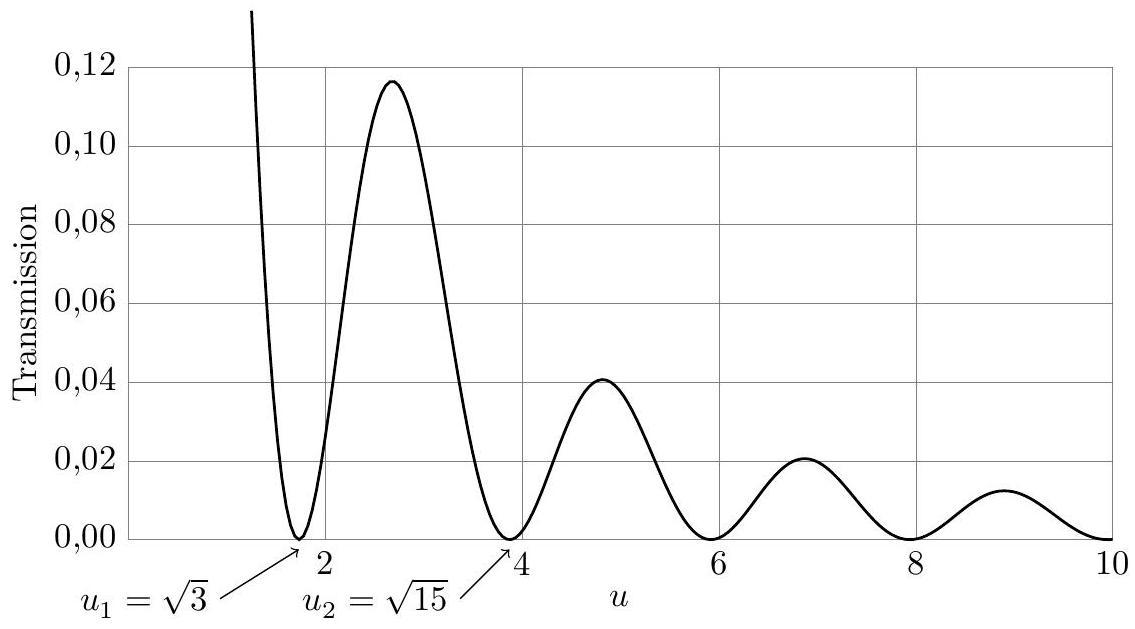
Figure 7
c) La figure 7 donne la courbe représentative de la fonction
d) Dans le cas où le polariseur de sortie est perpendiculaire au polariseur d'entrée, pouvez-vous sans calcul exprimer le facteur de transmission
d) Dans le cas où le polariseur de sortie est perpendiculaire au polariseur d'entrée, pouvez-vous sans calcul exprimer le facteur de transmission
III Détection électromagnétique de posture
Nous abordons dans cette partie l'étude du dispositif permettant de détecter la position et l'orientation de la tête du pilote par rapport au cockpit de l'hélicoptère. Il est constitué d'un «cube émetteur» d'environ 2 cm de côté, solidaire du cockpit et fixé au-dessus de la tête du pilote, et d'un «cube récepteur » identique au précédent, situé dans le casque du pilote. Les cubes sont constitués chacun de trois paires de bobines plates circulaires identiques, une paire par axe du cube. Chaque bobine plate est constituée de
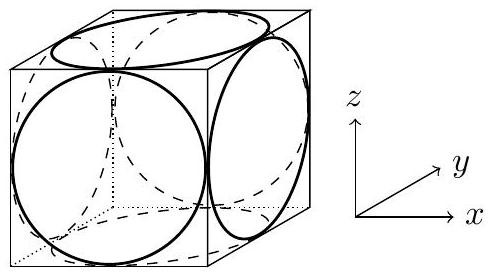
Figure 8
III.A - Paire de bobines parallèles
Chaque paire de bobines est disposée selon un arrangement particulier que l'on va déterminer et dont on va voir l'intérêt dans le contexte du problème posé.
III.A.1) Soit une bobine plate circulaire de centre
III.A.2) On considère maintenant deux bobines identiques à la précédente, de même axe de symétrie
a) Calculer le champ magnétique total en tout point
b) Montrer que le champ magnétique total en un point
III.A.1) Soit une bobine plate circulaire de centre
III.A.2) On considère maintenant deux bobines identiques à la précédente, de même axe de symétrie
a) Calculer le champ magnétique total en tout point
b) Montrer que le champ magnétique total en un point
III.A.3) À quelle condition sur
La disposition des bobines d'une paire qui vient d'être déterminée, parallèles et orientées dans le même sens, est donc celle qui réalise le mieux l'approximation dipolaire.
La disposition des bobines d'une paire qui vient d'être déterminée, parallèles et orientées dans le même sens, est donc celle qui réalise le mieux l'approximation dipolaire.
III.B - Détection de posture : principe de fonctionnement
Chaque paire de bobines parallèles émettrices est alimentée séquentiellement par un courant sinusoïdal de pulsation
Au cours de l'intervalle
III.B.1) La fréquence du signal alimentant les bobines émettrices vaut
La structure dipolaire du champ nous permet de connaître précisément la position du centre du cube récepteur par rapport au centre du cube émetteur
Dans la suite, on supposera, pour simplifier, que le centre
Au cours de l'intervalle
III.B.1) La fréquence du signal alimentant les bobines émettrices vaut
La structure dipolaire du champ nous permet de connaître précisément la position du centre du cube récepteur par rapport au centre du cube émetteur
Dans la suite, on supposera, pour simplifier, que le centre
III.B.2) On se place dans l'intervalle de temps
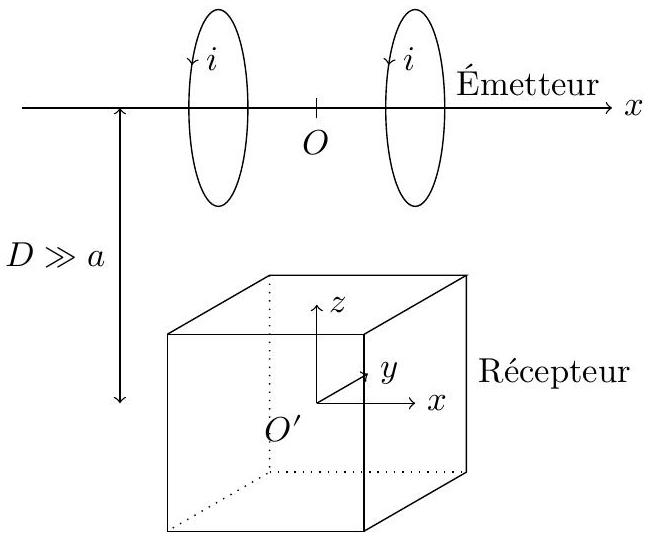
Figure 9
a) Que vaut le champ magnétique
b) Que vaut la force électromotrice
c) On suppose maintenant que le cube récepteur subit une rotation d'angle
d) On revient à l'état de référence et on fait subir au cube récepteur une rotation d'angle
e) On revient à l'état de référence et on fait subir au cube récepteur une rotation d'angle
f) Les résultats obtenus aux questions précédentes montrent que la force électromotrice
Montrer qu'on peut formellement écrire les résultats obtenus dans l'intervalle de temps [
III.B.3) On se place dans l'intervalle de temps [
III.B.4) Enfin, on se place dans l'intervalle de temps
III.B.5) Synthétiser les mesures effectuées au cours des trois intervalles de temps [
b) Que vaut la force électromotrice
c) On suppose maintenant que le cube récepteur subit une rotation d'angle
d) On revient à l'état de référence et on fait subir au cube récepteur une rotation d'angle
e) On revient à l'état de référence et on fait subir au cube récepteur une rotation d'angle
f) Les résultats obtenus aux questions précédentes montrent que la force électromotrice
Montrer qu'on peut formellement écrire les résultats obtenus dans l'intervalle de temps [
III.B.3) On se place dans l'intervalle de temps [
III.B.4) Enfin, on se place dans l'intervalle de temps
III.B.5) Synthétiser les mesures effectuées au cours des trois intervalles de temps [
Données numériques
| Célérité de la lumière dans le vide |
|
| Masse de l'électron |
|
| Charge élémentaire |
|
| Perméabilité magnétique du vide |
|
| Permittivité diélectrique du vide |
|
| Constante des gaz parfaits |
|
| Nombre d'Avogadro |
|
| Constante de Boltzmann |
|
| Constante de Planck |
|
Formulaire
Développement limité au voisinage de 0 :
Expression du champ magnétique créé par un dipôle magnétique
En réalité, le champ n'est pas parfaitement dipolaire du fait, notamment, des perturbations électromagnétiques de l'environnement. On doit alors réaliser une cartographie du champ magnétique dans la zone entourant le casque du pilote.
