Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

L'usage de calculatrices est interdit.

AVERTISSEMENT

Indiquer en tête de copie ou de chaque exercice le langage utilisé

Quel que soit le langage utilisé, le candidat pourra supposer qu'il dispose d'une fonction test_liste_vide qui prend en entrée une liste et renvoie le booléen 1 si la liste est vide et 0 sinon.

Le candidat pourra, s'il le juge utile, supposer que chaque liste se termine par un élément de marquage de fin de liste appelé

La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non justifiés ne seront pas pris en compte. Les candidats sont invités à encadrer les résultats de leurs calculs.

Exercice 1

Soit

un tableau non vide rempli avec des entiers naturels. Une pente positive (respectivement une pente négative) de longueur

est une suite de

indices consécutifs

sur lesquels

prend des valeurs croissantes

respectivement des valeurs décroissantes:

Ecrire la fonction :

MAXPENTEPOS données L:tableau d'entiers naturels
    résultat l:entier naturel

qui prend en entrée un tableau d'entiers naturels et renvoie la plus grande longueur de ses pentes positives.
2. Ecrire la fonction :

MAXPENTE données L:tableau d'entiers naturels
    résultat l:entier naturel

qui prend en entrée un tableau d'entiers naturels et renvoie la plus grande longueur de ses pentes (qu'elles soient positives ou négatives).

Exercice 2

Soit

un tableau de nombres entiers relatifs dont les cases sont numérotées de 1 à

. Si

sont deux entiers naturels tels que

, on note

le sous-tableau formé par les cases de

; on appelle sous-somme de

de la case

à la case

, et on note

, la somme des valeurs consécutives du sous-tableau

, c'est-à-dire

. On cherche la valeur maximale de toutes les sous-sommes de

. On se propose d'étudier différents algorithmes de résolution de ce problème.

Ecrire la fonction :

CUMUL données N:entier
    T: tableau d'entiers de longueur N
    résultat U:tableau d'entiers de longueur N

qui prend en entrée un tableau

d'entiers de longueur

et renvoie un tableau d'entiers de longueur

dont la

-ième case contient la sous-somme

, pour

compris entre 1 et

. On précisera la complexité de cet algorithme.
2. Ecrire la fonction :

MAXSOMME données N:entier
        T: tableau d'entiers de longueur N
    résultat k:entier

qui prend en entrée un tableau

de longueur

et renvoie une sous-somme maximale parmi les soussommes de ce tableau. On précisera la complexité de cet algorithme et on cherchera à minimiser cette complexité.
3. Une seconde méthode est basée sur le principe "diviser pour régner" : on divise le tableau en deux soustableaux de tailles presque égales. Proposer un algorithme récursif qui prend en entrée un tableau

de nombres entiers relatifs et calcule le quadruplet (

) tel que : Si

est un tableau à

cases numérotées de 1 à

est la somme ,
est le maximum des sous-sommes , pour compris entre 1 et ,
est le maximum des sous-sommes , pour et entiers tels que ,
est le maximum des sous-sommes , pour compris entre 1 et .

Quelle est la complexité de l'algorithme proposé?

Exercice 3

Les deux parties de cet exercice sont indépendantes.

On dispose d'une fonction ECHANGER qui prend en entrée un tableau d'entiers naturels et deux indices , compris entre 1 et la longueur du tableau , et échange les contenus des cases et dans le tableau.

On considère l'algorithme écrit en pseudo-langage:

PROC1 données $T$ : tableau[1..N] de 0,1
    variables $\quad I, J$ :entiers
    $I \leftarrow 1$
    $J \leftarrow N$
    tant que $I<J$ faire
        si $T[I]=0$ alors $I \leftarrow I+1$
        sinon ECHANGER $(T, I, J) ; J \leftarrow J-1$
        fin si
        fin faire

(a) Que fait ce programme sur le tableau

? Détailler son exécution.
(b) Démontrer que ce programme termine.
(c) Quel est le but de ce programme ? Le démontrer précisément.
(d) Proposer une implémentation de l'algorithme ci-dessus en remplaçant la boucle par une procédure récursive.
(e) Proposer un programme pour la fonction ECHANGER qui n'utilise pas une variable supplémentaire.
2. On dispose de deux fonctions:

La fonction par qui prend en entrée un entier naturel et renvoie la valeur 0 si cet entier est pair et 1 si cet entier est impair,
la fonction ent qui prend en entrée un nombre rationnel et renvoie sa partie entière.

On considère l'algorithme écrit en pseudo-langage:

PROC2 données $I, J$ : entiers
    variables $\quad t$ :entier
        $t \leftarrow 0$
    tant que $I \geq 1$ faire
        si $\operatorname{par}(I)=1$ alors $t:=t+J$
        fin si
        $J \leftarrow 2 * J$
        $I \leftarrow \operatorname{ent}(I / 2)$
        fin faire
    Retourner $t$

(a) Ecrire l'exécution de ce programme sur les entiers

.
(b) Ecrire l'exécution de ce programme sur les entiers

.
(c) Que calcule ce programme? Le justifier précisément.

Exercice 4

Soit

un alphabet fini. On note

l'ensemble des mots finis écrits avec des lettres de

.
On rappelle la définition : Soient

deux mots dans

. Soient

dans

tels que

. On dit que

est un facteur de

et s'il existe un entier naturel

compris entre 0 et

tel que, pour tout

compris entre 1 et

.
Soit

l'ensemble des automates finis

tels que :

L'ensemble des états est un ensemble fini, réunion d'un singleton et d'une partie de l'ensemble .
L'état est l'unique état initial.
L'ensemble est une partie de désignant l'ensemble des états finals.
désigne l'ensemble des transitions. Il vérifie la propriété : Pour toute lettre dans l'alphabet , les transitions étiquetées par la lettre ne peuvent aboutir que dans l'état .

En raison de cette dernière propriété, dans un automate de l'ensemble

, l'étiquette d'une transition est déterminée par l'état d'arrivée de la transition. Pour cette raison, si

est un automate de l'ensemble

, si

sont deux lettres de

telle qu'il existe une transition de l'état

vers l'état

dans

, on note

cette transition et son étiquette est alors

.
Un exemple d'un tel automate sur l'alphabet à trois lettres

est donné par la figure 1. Pour cet automate

On note

l'ensemble des langages reconnus par les automates de l'ensemble

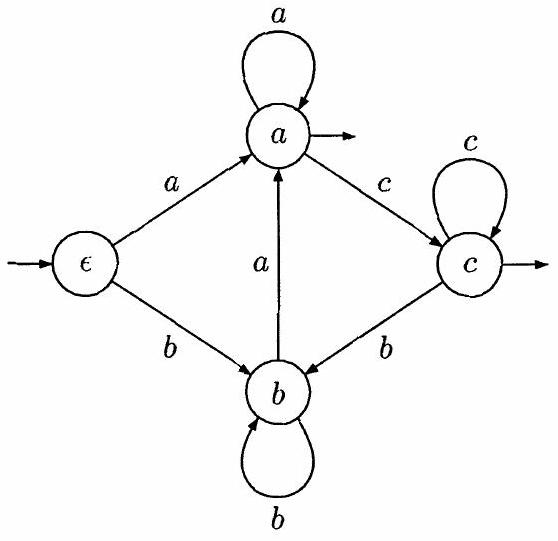
Figure 1: L'automate

de l'ensemble

Dans le cas particulier où est l'alphabet à une lettre , dresser la liste des (six) langages de l'ensemble . Pour chacun d'eux, on dessinera un automate de l'ensemble le reconnaissant.
On considère le cas particulier où est l'alphabet à trois lettres .
(a) Démontrer que le langage réduit au singleton appartient à . On dessinera explicitement un automate dans qui reconnait le langage ( ).
(b) Démontrer que le langage appartient à . On dessinera explicitement un automate dans qui reconnait le langage .
On revient au cas général. Soit un entier naturel . Soit un mot de longueur dans . On note le langage réduit au singleton .
(a) On suppose les lettres distinctes deux à deux.
i. Démontrer que est dans .
ii. Démontrer que est dans .
(b) Réciproquement, on suppose que le langage est dans . Démontrer que les lettres sont distinctes deux à deux.
Démontrer qu'un automate de est un automate déterministe.
Soit un langage dans reconnu par un automate dans . Démontrer que le langage est dans . On pourra utiliser l'automate pour construire un automate dans qui reconnait .
Soient et deux parties de et soit une partie formée de mots de longueur 2 . On note le langage formé par les mots dans dont la première lettre est dans , la dernière lettre est dans et ne contenant aucun facteur de longueur 2 dans .
(a) Dans le cas particulier où est l'alphabet à deux lettres et , décrire précisément le langage .
(b) Dans le cas particulier où est l'alphabet à trois lettres , déterminer et tels que .
(c) Toujours dans le cas particulier où est l'alphabet à trois lettres , déterminer et tels que désignant le langage reconnu par l'automate de la figure 1.
(d) On revient au cas général. Démontrer que le langage est dans .
(e) Soit un langage dans . On note l'ensemble des lettres dans telle qu'il existe un mot de dont la première lettre est . On note l'ensemble des lettres dans telle qu'il existe un mot de dont la dernière lettre est . On note l'ensemble complémentaire des facteurs de longueur 2 de mots de . On suppose que est un langage dans ne contenant pas le mot vide. Démontrer que .
On se donne des lettres , distinctes deux à deux. On considère les langages définis récursivement par : et, , pour un entier . Soit un entier .
(a) Démontrer que est un langage de .
(b) Proposer un algorithme qui prend en entrée l'entier naturel et retourne un automate de qui reconnait .
s!u.nof słuəunnoop sәุ.dde,a - ztol & 1 - дSIOHJ NI