Version interactive avec LaTeX compilé
CONCOURS ARTS ET MÉTIERS ParisTech - ESTP - POLYTECH
Durée 4 h
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
L'usage de calculatrices est autorisé.
AVERTISSEMENT
- Les données et formules utiles à la résolution du sujet figurent en fin d'énoncé.
- Tout au long de l'énoncé, les paragraphes en italique ont pour objet d'aider à la compréhension du problème.
- Tout résultat fourni dans l'énoncé peut être admis et utilisé par la suite, même s'il n'a pas été démontré par le(la) candidat(e).
- Le sujet comporte une résolution de problème. Elle devra présenter de manière claire une démarche scientifique détaillée et basée, d'une part sur les documents fournis, et d'autre part sur les connaissances du candidat. Toute tentative de réponse pertinente, même incomplète, sera prise en compte lors de la notation.
- À titre indicatif, une durée conseillée pour traiter chaque partie est indiquée en début de partie.
PREMIÈRE PARTIE OPTIMISATION DE RENDEMENTS THERMODYNAMIQUES
Lors de chaque étape de conversion d'énergie se pose la question du rendement, primordiale au niveau des applications. Alors que les moteurs et alternateurs réalisent une conversion de puissance électrique-mécanique quasi-totale, les machines thermiques présentent des limites strictes issues de la thermodynamique. Enoncées pour la première fois par Carnot, elles sont de nos jours abordées industriellement sous la forme du rendement à puissance maximale, menant à des résultats plus pertinents mais légèrement moins généraux. Nous traitons dans une première partie son application aux centrales nucléaires, géothermiques ou encore à combustible fossile.
La conversion d'énergie dans les piles peut aussi être abordée en thermochimie, le «rendement thermodynamique » étant rencontré assez couramment, surtout dans le milieu anglosaxon. Son interprétation est cependant différente de celle liée à une machine ditherme et sera discutée dans une seconde partie.
RENDEMENT À PUISSANCE MAXIMALE (
A / Cycle de Carnot
On considère un moteur ditherme fonctionnant entre une source chaude de température
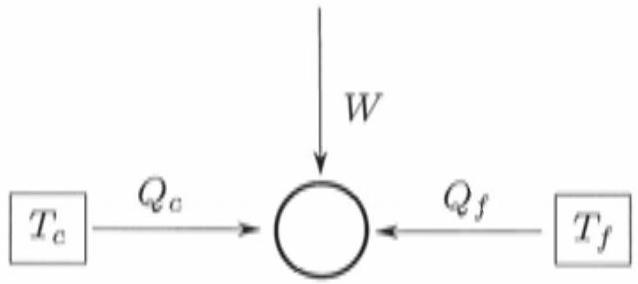
Figure 1 - Schéma général d'une machine ditherme.
A1. Lors du fonctionnement de la machine, quels sont les signes de
A2. Définir le rendement
A2. Définir le rendement
Ce rendement est obtenu pour un cycle de Carnot, constitué de quatre transformations : deux adiabatiques et deux isothermes.
A3. Lors des phases isothermes, fluide et thermostat sont à la même température : qu'est-ce que cela implique sur les transferts thermiques? Cela vous parait-il raisonnable industriellement?
A4. Sur le tableau de la figure 2 sont indiqués les rendements de différentes centrales électriques (
| Centrale électrique |
|
|
|
| Centrale à charbon (West Thurrock - Angleterre) | 25 | 565 | 0,36 |
| Centrale nucléaire (Canada) | 25 | 300 | 0,3 |
| Centrale géothermique (Larderello - Italie) | 80 | 250 | 0,16 |
Figure 2 - Rendements de certaines installations électriques.
B / Origine des résistances thermiques
Le cycle précédent présente un rendement optimal, le rendement de Carnot. Cependant, la propriété principale d'un moteur n'est pas son rendement, mais sa puissance maximale : pour cela, on diminue volontairement la température associée au contact avec la source chaude de
Une conduite cylindrique de cuivre de conductivité thermique
B1. Rappeler la loi de Fourier reliant le vecteur densité de courant thermique
B2. Schématiser la géométrie du problème. Justifier que
B3. On note
B2. Schématiser la géométrie du problème. Justifier que
B3. On note
B4. Justifier que le flux
B5. En déduire l'expression de la différence de température
B6. Rappeler la définition de la résistance thermique. Donner son unité. Quelle analogie peut-on faire avec l'électrocinétique et sous quelle(s) condition(s) est-elle valide?
B5. En déduire l'expression de la différence de température
B6. Rappeler la définition de la résistance thermique. Donner son unité. Quelle analogie peut-on faire avec l'électrocinétique et sous quelle(s) condition(s) est-elle valide?
B7. Déterminer l'expression de la résistance thermique
C / Rendement à puissance maximale
Les résistances thermiques étant décrites, on s'intéresse au fonctionnement général de la machine thermique. Ce travail, réalisé dans la seconde moitié du
On considère le cycle thermodynamique suivant :
On considère le cycle thermodynamique suivant :
- Une transformation adiabatique menant le fluide de
à ; - une transformation isotherme à
associée à un transfert thermique avec la source froide de température ; - une transformation adiabatique menant le fluide de
à ; - une transformation isotherme à
, associée à un transfert thermique avec la source chaude de température . On note sa durée et la résistance thermique associée .
Toutes les transformations du fluide sont supposées réversibles et la durée totale du cycle est notée, où est une constante. Le schéma de la figure 3 résume la situation.
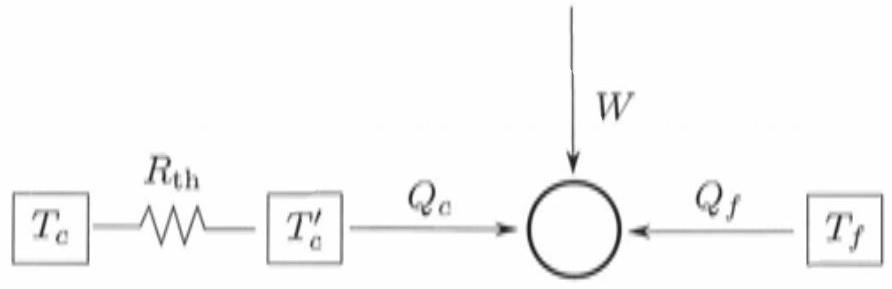
Figure 3 - Prise en compte d'une résistance thermique.
C1. Exprimer le transfert thermique
C2. Écrire les premier et second principes de la thermodynamique pour le fluide considéré.
C3. A l'aide des questions précédentes, exprimer la puissance moyenne fournie par la machine thermique
C4. Quelle doit être la valeur de
C5. Exprimer le rendement dans ces conditions en fonction de
C6. La machine thermique dans son ensemble ne fonctionne pas de manière réversible. Proposer des sources d'irréversibilité à considérer lors d'une utilisation pratique.
C2. Écrire les premier et second principes de la thermodynamique pour le fluide considéré.
C3. A l'aide des questions précédentes, exprimer la puissance moyenne fournie par la machine thermique
C4. Quelle doit être la valeur de
C5. Exprimer le rendement dans ces conditions en fonction de
C6. La machine thermique dans son ensemble ne fonctionne pas de manière réversible. Proposer des sources d'irréversibilité à considérer lors d'une utilisation pratique.
RENDEMENT THERMODYNAMIQUE DES PILES (
Les réactions de combustions sont principalement utilisées dans les moteurs à explosion. Cependant, elles peuvent aussi produire de la lumière, comme le montrent les couleurs bleues des flammes (issues de la recombinaisons de radicaux), ou encore de l'électricité via des réactions électrochimiques. C'est à cette dernière forme de transformation d'énergie que l'on s'intéresse ici, en étudiant un équivalent pour les piles du rendement d'un moteur thermique.
On s'intéresse à un système
On s'intéresse à un système
-
est le transfert thermique fourni au milieu extérieur lorsqu'aucun travail électrique n'est tiré de la réaction. est, dans ces conditions, le transfert thermique algébrique reçu par le système ; -
est le travail électrique maximal fourni au milieu extérieur lorsqu'un travail électrique est tiré de la réaction. est le travail électrique algébriquement reçu par .
On s'intéressera successivement à l'évaluation de ces différents termes en s'appuyant sur la réaction de combustion de l'hydrogène, puis on discutera le sens physique du rendement thermodynamique.
D / Expression du transfert thermique
On modélise l'évolution chimique du système lors de la combustion de l'hydrogène par la réaction suivante:
Cette réaction a lieu à l'air libre de température
D1. Dans quel but cette réaction peut-elle être utilisée en travaux pratiques?
D2. Citer une application industrielle la mettant en jeu.
D3. Rappeler la définition d'une grandeur de réaction et de l'enthalpie
D4. Estimer numériquement
D5. Établir que
D6. Dans quelle(s) condition(s) la température atteignable au cours de cette combustion (la température de flamme) est-elle maximale?
D7. Déterminer dans ce cas la valeur de cette température maximale. On se placera dans le cas d'un milieu contenant uniquement du dihydrogène et du dioxygène en proportions stœchiométriques et on détaillera avec soin le raisonnement utilisé.
D2. Citer une application industrielle la mettant en jeu.
D3. Rappeler la définition d'une grandeur de réaction et de l'enthalpie
D4. Estimer numériquement
D5. Établir que
D6. Dans quelle(s) condition(s) la température atteignable au cours de cette combustion (la température de flamme) est-elle maximale?
D7. Déterminer dans ce cas la valeur de cette température maximale. On se placera dans le cas d'un milieu contenant uniquement du dihydrogène et du dioxygène en proportions stœchiométriques et on détaillera avec soin le raisonnement utilisé.
E / Expression du travail électrique
Il est possible de générer un travail électrique via cette réaction chimique en séparant spatialement les deux réactifs : on parle de pile à combustible. Une membrane échangeuse de protons mais de résistance électrique élevée sépare alors l'anode de la cathode, où ont lieu des réactions d'oxydo-réduction différentes menant au même bilan global que précédemment. L'évolution est supposée isobare (à pression
E1. Le dihydrogène joue-t-il le rôle d'oxydant ou de réducteur? Écríre la demiéquation d'oxydoréduction associée.
E2. Le dioxygène joue-t-il le rôle d'oxydant ou de réducteur? Écrire la demi-équation d'oxydoréduction associée.
E3. Quelle est la définition d'un potentiel thermodynamique et de l'enthalpie libre
E4. Sous quelle condition l'enthalpie libre est-elle un potentiel thermodynamique? Quelle contrainte cela impose-t-il sur le signe de
E2. Le dioxygène joue-t-il le rôle d'oxydant ou de réducteur? Écrire la demi-équation d'oxydoréduction associée.
E3. Quelle est la définition d'un potentiel thermodynamique et de l'enthalpie libre
E4. Sous quelle condition l'enthalpie libre est-elle un potentiel thermodynamique? Quelle contrainte cela impose-t-il sur le signe de
Pour la suite de l'étude, on se placera dans les conditions standard.
E5. En partant des premier et second principes de la thermodynamique, montrer que le travail électrique maximal fourni par la pile
E6. A quel cas correspond la limite
E7. On donne
E8. Évaluer numériquement le travail maximal fourni par la réaction d'une mole de dihydrogène.
E5. En partant des premier et second principes de la thermodynamique, montrer que le travail électrique maximal fourni par la pile
E6. A quel cas correspond la limite
E7. On donne
E8. Évaluer numériquement le travail maximal fourni par la réaction d'une mole de dihydrogène.
Les contraintes environnementales actuelles ont entraîné le développement de la filière hydrogène : on remarque que la combustion étudiée ici ne génére pas de dioxyde de carbone.
E9. Comment est-il possible de synthétiser du dihydrogène de manière "verte", c'est-è-dire notamment sans produire de dioxyde de carbone?
E10. Quelle est la principale limite à son utilisation massive comme vecteur d'énergie?
E10. Quelle est la principale limite à son utilisation massive comme vecteur d'énergie?
F / Rendement thermodynamique
Dans cette partie, comme dans la fin de la précédente, nous travaillons dans les conditions standard.
F1. Quelle(s) analogie(s) et différence(s) existe-t-il entre la définition du rendement thermodynamique pour une pile et pour une machine thermique ditherme?
F2. Exprimer le rendement thermodynamique à partir des grandeurs de réaction standard relatives à l'enthalpie et l'entropie et l'évaluer numériquement dans le cas de la réaction étudiée.
F3. Dans les situations proposées suivantes, déterminer si la réaction chimique est thermodynamiquement possible, auquel cas donner une limite inférieure au rendement thermodynamique:
F2. Exprimer le rendement thermodynamique à partir des grandeurs de réaction standard relatives à l'enthalpie et l'entropie et l'évaluer numériquement dans le cas de la réaction étudiée.
F3. Dans les situations proposées suivantes, déterminer si la réaction chimique est thermodynamiquement possible, auquel cas donner une limite inférieure au rendement thermodynamique:
-
et . -
et .
Pour certaines piles, notamment les piles de concentration, la réaction associée est, en l'absence de travail autre que celui des forces de pression, athermique.
F4. Y a-t-il transformation d'énergie de liaison en travail électrique lors du fonctionnement d'une telle pile?
F5. Évaluer dans ce cas la variation d'enthalpie
F6. Peut-on parler de rendement thermodynamique dans ce cas?
F7. En conclusion, le rendement thermodynamique pour une pile est-t-il associé à des contraintes similaires à celui d'un moteur ditherme? Quel peut-être son intérêt pratique?
F4. Y a-t-il transformation d'énergie de liaison en travail électrique lors du fonctionnement d'une telle pile?
F5. Évaluer dans ce cas la variation d'enthalpie
F6. Peut-on parler de rendement thermodynamique dans ce cas?
F7. En conclusion, le rendement thermodynamique pour une pile est-t-il associé à des contraintes similaires à celui d'un moteur ditherme? Quel peut-être son intérêt pratique?
SECONDE PARTIE
Conversion d'énergie électrostatique par les phénomènes atmosphériques et nucléaires
L'utilisation des phénomènes électriques comme ressource énergétique peut être envisagée dans deux domaines très différents de la physique dont nous cherchons à évaluer les ordres de grandeur. D'une part, lors des orages, où suite aux travaux pionniers de Benjamin Franklin le lien entre électricité et foudre a été démontré. D'autre part en physique nucléaire, où le moteur d'une réaction de fission est essentiellement électrostatique.
ÉNERGIE DES ÉCLAIRS (
Document 1. Panorama de la physique, Édition Belin, 2007:
On est souvent étonné d'apprendre l'existence d'un champ électrique permanent dans l'atmosphère. Entre la haute atmosphère, vers 50 km , et la surface terrestre, la différence de potentiel est de 300 kV . [...] Quel est le générateur capable de maintenir 300 kV entre la surface et l'électrosphère malgré [l'existence d'un] courant de fuite ? Il a fallu attendre 1920 pour que C.T.R Wilson, prix Nobel de physique, l'identifie. Il s'agit des nuages, très développés pendant un orage, les cumulonimbus, qui sont chargés positivement dans leur partie haute et froide, et négativement dans leur partie basse et chaude. Ces charges électriques apparaissent en même temps que les chutes de grêle, signe que leur formation est líée à ces précipitations. [...] Lors du développement du nuage, la charge électrique de sa base induit une forte différence de potentiel avec le sol. Dès que [le champ électrique] atteint quelques
On est souvent étonné d'apprendre l'existence d'un champ électrique permanent dans l'atmosphère. Entre la haute atmosphère, vers 50 km , et la surface terrestre, la différence de potentiel est de 300 kV . [...] Quel est le générateur capable de maintenir 300 kV entre la surface et l'électrosphère malgré [l'existence d'un] courant de fuite ? Il a fallu attendre 1920 pour que C.T.R Wilson, prix Nobel de physique, l'identifie. Il s'agit des nuages, très développés pendant un orage, les cumulonimbus, qui sont chargés positivement dans leur partie haute et froide, et négativement dans leur partie basse et chaude. Ces charges électriques apparaissent en même temps que les chutes de grêle, signe que leur formation est líée à ces précipitations. [...] Lors du développement du nuage, la charge électrique de sa base induit une forte différence de potentiel avec le sol. Dès que [le champ électrique] atteint quelques
Document 2. Atmosphère, océan et climat, Édition Belin, 2007:
Description d'un cumulonimbus
Description d'un cumulonimbus
- Hauteur basse : 400 m à 1 km
- Épaisseur : Plusieurs km
- Composition : liquide et glace
- Précipitations : Forte pluie, parfois grêle
- Aspect : Nuage dense à extension verticale considérable se développant à partír de cumulus congestus. Sa partie supérieure s'étale souvent en forme d'enclume. C'est le nuage d'orage.
Document 3. Donnée issue de Météo-France :
Nombre moyen d'impacts de foudre au sol par
Nombre moyen d'impacts de foudre au sol par
Document 4. La vie du rail - Hors série - Le TGV Nord Europe, 1993 : Fiche technique du TGV Réseau
- Vitesse maximale en service commercial :
- Puissance aux arbres des moteurs de traction sous
- Puissance aux arbres des moteurs de traction sous
- Puissance unitaire des moteurs de traction : 1100 kW
- Nombre de moteurs de traction : 8
G / Résolution de problème
G1. Combien de temps pourrait-on faire avancer un TGV en récupérant durant un an toute l'énergie issue des éclairs frappant une grande ville française?
Cette résolution de problème devra présenter de manière claire une démarche scientifique détaillée et basée, d'une part sur les documents fournis, et d'autre part sur les connaissances du candidat. Toute tentative de réponse pertinente, même incomplète, sera prise en compte lors de la notation.
ÉNERGIE D'UN NOYAU (
La filière nucléaire représente actuellement près de
Le noyau atomique est modélisé par une boule de rayon
Le noyau atomique est modélisé par une boule de rayon
H / Champ électrostatique
Nous utilisons les coordonnées sphériques (
H1. Lister les invariances de la distribution volumique de charge. Qu'en déduit-on pour le champ électrostatique?
H2. Par l'utilisation de symétries, montrer que le champ créé en un point
H3. Déterminer ce champ en un point
H4. Déterminer ce champ en un point
H1. Lister les invariances de la distribution volumique de charge. Qu'en déduit-on pour le champ électrostatique?
H2. Par l'utilisation de symétries, montrer que le champ créé en un point
H3. Déterminer ce champ en un point
H4. Déterminer ce champ en un point
I / Énergie électrostatique
I1. Rappeler l'expression de la densité volumique d'énergie liée au champ électrique.
I2. Montrer que dans le cas présent, l'énergie électrostatique totale
I2. Montrer que dans le cas présent, l'énergie électrostatique totale
I3. En déduire que
où
J / Réaction de fission
De nombreuses réactions de fission différentes mettant en jeu l'uranium 235 se passent au sein d'un réacteur nucléaire. Nous nous intéressons à l'une d'entre elles, dont le bilan est :
Cette réaction libère une énergie de l'ordre de 200 MeV . Les données situées à la fin du sujet comprennent la constante de Coulomb ainsi que la densité volumique de nucléons dans le noyau.
J1. Quels noyaux peuvent être concernés par une réaction de fission?
J2. Évaluer le rayon
J3. En déduire l'énergie électrostatique libérée lors de la réaction de fission et comparer sa valeur à celle annoncée.
J4. Cette approche permet-elle d'expliquer le phénomène de fusion nucléaire?
J1. Quels noyaux peuvent être concernés par une réaction de fission?
J2. Évaluer le rayon
J3. En déduire l'énergie électrostatique libérée lors de la réaction de fission et comparer sa valeur à celle annoncée.
J4. Cette approche permet-elle d'expliquer le phénomène de fusion nucléaire?
DONNÉES
- Énergies de liaison :
-
-
- Capacités thermiques molaires à pression constante, supposées indépendantes de la température :
-
, -
. - Gradient et divergence en coordonnées cylindriques :
- Constante de Coulomb :
- Densité volumique de nucléons dans le noyau :
