Depuis les premières observations de signaux de résonances nucléaires en 1945, le magnétisme nucléaire s'est très largement développé initialement dans le domaine de la physique et de la chimie puis dans les domaines de la biologie et de la médecine. Le prix Nobel de médecine 2003 a ainsi été attribué à P.C. Lauterbur et P. Mansfield pour leurs travaux sur "I'lmagerie par Résonance Magnétique", version médicalisée des techniques par " Résonance Magnétique Nucléaire" des physiciens et chimistes.

La RMN est un phénomène apparaissant dans les systèmes magnétiques possédant un moment cinétique et un moment magnétique . Nous nous limiterons dans ce problème au cas du proton qui est le moment magnétique le plus présent dans les milieux biologiques.

Les grandeurs vectorielles sont notées en gras. Le référentiel fixe ( ) est caractérisé par le repère orthogonal ( ). On rappelle que l'expression du couple exercée par un champ magnétique sur un moment magnétique est donné par . L'énergie potentielle associée est donnée par-m.B.

Le moment cinétique et le moment magnétique du proton sont proportionnels:

où est le " facteur gyromagnétique ".
1/ Pour évaluer l'ordre de grandeur de dans le cas du proton, il est suffisant d'utiliser un modèle simpliste dans lequel ce proton de charge e est en mouvement circulaire uniforme sur une orbite circulaire de rayon , égale à la taille du noyau.

1a: Donner la définition du moment magnétique en fonction du courant I associé au mouvement du proton et du rayon . En déduire l'expression du moment magnétique en fonction de la charge , la vitesse du proton et du rayon .

1b: Donner la définition du moment cinétique . On notera la masse du proton. Calculer son module.

1c: Montrer que dans ce modèle, le facteur gyromagnétique est donné par :

1d: Le modèle précèdent donne le bon ordre de grandeur du facteur gyromagnétique mais doit être corrigé d'un facteur multiplicatif différent pour chaque noyau, pour obtenir le facteur gyromagnétique réel. Ce facteur a été déterminé par Rabi en 1936 et vaut 5.58 pour le proton. Calculer le facteur gyromagnétique correspondant. On prendra et .

2/ En fait, le moment cinétique associé au proton correspond à une contribution de "spin", purement "quantique" sans équivalent classique (une approche naïve associe le spin à la rotation du proton sur lui-même). Ce caractère "quantique" lui impose en présence d'un champ magnétique de ne prendre que deux valeurs ou où h est une constante dite "de Planck" Dans la suite de l'énoncé, ces deux valeurs seront associées à un proton se trouvant respectivement dans " l'état + " et " l'état - ".

2a: Donner l'expression des énergies magnétiques et associées à un proton se trouvant dans " l'état + " et " l'état - " en fonction de et . Quelle est l'énergie la plus basse? Montrer que la valeur absolue de la différence d'énergie entre ces deux " états " est proportionnelle à . Nous définissons la pulsation telle que . Donner l'expression de la pulsation en fonction de et .

2 b : Considérons un champ magnétique de 10 T , calculer la valeur de pour des protons (on prendra ). Comparer cette énergie à celle des fluctuations thermiques à (on prendra )

3/ On définit et les nombres par unité de volume de protons qui peuplent "l'état + " et " l'état - " à l'instant , ; ces nombres ne sont pas connus à ce stade car on étudie une situation hors d'équilibre. Après avoir donné l'expression des moments magnétiques associés à chacun des états, en déduire une expression de l'aimantation correspondante en fonction de et h .

4/ La différence d'énergies entre "l'état + " et " l'état - " étant inférieure aux fluctuations d'énergie thermique associées à l'environnement, des transitions entre les deux états sont possibles. Nous pouvons ainsi définir la probabilité pour qu'un proton passe d'un " état+ " à un " état- " pendant une unité de temps et P - pour qu'un proton passe d'un " état- " à un " état+ " pendant une unité de temps

4a: Considérons tout d'abord "l'état + ". La loi d'évolution du nombre est donnée par:

Justifier cette équation en donnant un sens physique à chacune des contributions. En déduire l'équation devant être vérifiée par N.(t).

4b : On définit . Quel est le sens physique de cette grandeur ? Montrer que constante.

4c: On définit . Etablir l'équation d'évolution devant être vérifiée par . Montrer que cette équation peut se mettre sous la forme où et sont des constantes. Exprimer et en fonction de - et N .

4d: En déduire que l'équation devant être vérifiée par la composante de l'aimantation s'écrit :

En déduire . Que représente ?
5/ A l'équilibre thermodynamique, le nombre de protons par unité de volume équi (respectivement équi ) est donné par la relation de Boltzmann (respectivement ) où est une constante et la température.

5 a : Montrer que . Donner l'expression au premier ordre de . lorsque (ce qui est généralement le cas)

5b : En déduire que .
5 c : Calculer la valeur de pour un champ magnétique de 10 T à . Que peut-on en conclure concernant cette différence de populations ?

6/ Ecrire l'expression de correspondante. En déduire l'expression de la susceptibilité statique en fonction de et .

Le comportement de l'aimantation d'un échantillon contenant des protons peut également être étudié en considérant les lois d'évolution de ses composantes du point de vue classique. Considérons donc un échantillon de volume unité caractérisé par une aimantation macroscopique ( ) placé dans un champ magnétique parallèle comme précédemment à l'axe OZ . A l'instant initial, nous supposons que cette aimantation est dans le plan (XOZ) et est caractérisée par le vecteur .

Nous négligeons dans un premier temps les contributions dites "de relaxation " du type de celles introduites à la question de la partie . Le système est dit " libre ".

1a: Donner l'expression du couple exercé par le champ magnétique sur l'échantillon en fonction de son aimantation et du champ magnétique .

1b : Ecrire l'équation de mouvement du moment cinétique associé correspondant dans le référentiel fixe ( ).

1c: Montrer que l'équation décrivant l'évolution de l'aimantation s'écrit :

2/ Montrer que la norme de reste constante au cours de ce mouvement. Montrer que l'angle entre et défini par reste également constant. En déduire la nature du mouvement de l'aimantation .

3/ Projeter l'équation d'évolution sur l'axe OZ . En déduire l'expression de .
4/ Projeter l'équation d'évolution selon les axes OX et OY . En déduire les expressions de et . En associant ces expressions à celle obtenue pour (t), vérifier les résultats obtenus en B2.

5/ II est en fait commode d'écrire ces équations dans le référentiel tournant ( O , x, y, z), l'axe Oz est confondu avec OZ, le vecteur rotation . A l'instant , l'axe Ox est confondu avec l'axe OX. Nous admettrons que l'évolution de dans le référentiel fixe sous l'effet du champ magnétique est la même que l'évolution de dans le référentiel tournant sous l'effet d'un champ magnétique effectif . Ecrire les équations d'évolution des composantes ( , ) de l'aimantation dans le référentiel tournant ( ). Montrer qu'un choix judicieux de que l'on précisera permet d'avoir des composantes indépendantes du
temps dans le référentiel tournant. Expliciter alors ces composantes en fonction de et .

6/ En déduire les composantes de l'aimantation dans le référentiel fixe ( ), on vérifiera que les résultats obtenus sont cohérents avec ceux des questions 3 et 4.

L'étude menée dans la partie A montre que l'on devrait avoir une aimantation parallèle à , ce qui n'est pas le cas à ce stade de la modélisation. Pour affiner le modèle, il faut introduire les contributions associées aux phénomènes de relaxation qui rendent compte de l'interaction de l'aimantation avec son environnement. L'équation d'évolution de est alors donnée par l'équation dite de "Bloch " établie en 1946 :

où représente l'aimantation à l'équilibre décrite dans la partie et le temps de relaxation qui est en général tel que . Pour obtenir l'équation correspondante dans le référentiel tournant ( ), il convient simplement de remplacer le champ magnétique par le champ magnétique effectif défini à la question 4.
Ecrire dans le référentiel tournant caractérisé par le vecteur l'équation d'évolution de . En déduire la loi d'évolution . Comment qualifie-t-on la nature de ce mouvement?

8/ Ecrire dans le référentiel tournant caractérisé par le vecteur les équations d'évolution des composantes et .

9/ Pour déterminer les lois d'évolution et il est commode d'introduire . Etablir l'équation d'évolution de .

10/ Calculer la loi d'évolution . En déduire les lois d'évolution des composantes et dans le référentiel tournant ( ).

11/ Que deviennent ces lois si le référentiel tournant retenu est celui dans lequel l'aimantation reste dans le plan ( ) ?

12/ En déduire les lois d'évolution des composantes et dans le référentiel fixe ( ). Comment qualifie-t-on la nature de ce mouvement?

13/ Vérifier que le modèle adopté est cohérent avec les résultats de la partie ? Quel est l'ordre de grandeur du temps caractéristique d'évolution vers l'état d'équilibre?

Les techniques classiques de RMN font intervenir un champ magnétique oscillant perpendiculaire au champ magnétique statique avec . L'objectif de cette partie est de déterminer les lois d'évolution de l'aimantation dans le référentiel fixe lorsque le système magnétique est soumis à ces deux champs croisés.

Comme dans la partie B , nous négligeons dans un premier temps les contributions dites " de relaxation" décrites par les équations de Bloch (Voir question 7 de la partie B).

1/ Supposons que le champ oscillant soit de la forme avec . Décrire sommairement un dispositif expérimental permettant de produire un tel champ.
Ecrire l'équation d'évolution de l'aimantation dans le référentiel fixe.
3/ En procédant comme dans la question B 5 , caractériser le référentiel ( , ) associé au repère ( ) dans lequel le champ magnétique est statique ? Montrer que dans ce référentiel particulier l'aimantation est soumise à un champ effectif constant. Préciser l'angle entre ce champ et le champ .

4/ Montrer que l'aimantation suit dans ce référentiel ( ) un mouvement périodique qu'il conviendra de préciser. Donner l'expression de la pulsation de ce mouvement en fonction de , et où et .

5/ Montrer que les composantes de dans ce référentiel ( ) sont solutions du système différentiel :

6/ Supposons que le champ magnétique oscille à une pulsation très éloignée de la pulsation de Larmor . En reprenant le résultat obtenu en 3 , donner à l'ordre 0 l'orientation et l'intensité du champ magnétique effectif Expliquer qualitativement ce phénomène.

7/ Supposons maintenant que le champ oscille à la pulsation telle que soit égale à la pulsation de Larmor .
7a : Quelle est alors l'orientation du champ effectif caractérisé par l'angle . En déduire les caractéristiques du mouvement de l'aimantation.
7 b: Ecrire dans ce cas les équations d'évolution des composantes de dans le référentiel ( ).

8/ Considérons maintenant un système initialement à l'équilibre dans le champ magnétique statique et appliquons lui à l'instant une impulsion de champ de durée . La pulsation associée à est choisie telle que .
8 a: Quel est l'ordre de grandeur du temps nécessaire pour que l'aimantation se retrouve perpendiculaire à . Une telle impulsion de durée est dite " de ".
8 b : Si on coupe le champ après une durée , quel sera le mouvement ultérieur de l'aimantation? Supposons de plus que les inhomogénéités locales du champ magnétique induisent une légère dispersion de la fréquence de Larmor de moments magnétiques individuels ( ), montrer qualitativement qu'après une impulsion de les orientations des moments individuels contribuant à l'aimantation se dispersent. Quelle est la dispersion angulaire des orientations de moments un temps t après la fin de l'impulsion de ? On applique alors une impulsion dite "de "sur le système (on précisera sa durée) Décrire qualitativement le comportement ultérieur des moments individuels après la coupure de cette impulsion? Au bout de combien de temps la dispersion des orientations des moments individuels est-elle redevenue nulle ? On parle alors "d'Echo de spins".

Nous introduisons maintenant les contributions associées aux phénomènes de relaxation. On suppose que (on limitera les calculs à l'ordre 1 en ) et la pulsation est dans la suite redevenue quelconque.

9 / Réécrire les équations d'évolution des composantes de l'aimantation dans le référentiel ( ) d'un système soumis aux champs croisées et en tenant compte de la relaxation décrite par les équations de Bloch.

10/, En admettant que les composantes et sont proportionnelles à , montrer en les explicitant que la composante obéit à une équation d'évolution à l'ordre 0 en .

11/ Calculer en régime stationnaire.
12/ Montrer que les composantes et obéissent à un système d'équations couplées d'ordre 1 en .

13/ Résoudre ce système d'équations et montrer qu'en régime stationnaire:

14/ Calculer l'amplitude de l'aimantation transverse correspondante. Calculer la pulsation pour laquelle cette amplitude est maximale. Comparer cette amplitude maximale à celle qui aurait été obtenue si le système avait été soumis à un unique champ statique d'intensité . On parle alors de " résonance ".

15/ Dans la pratique, le champ oscillant n'est en général pas un champ circulaire comme celui décrit mais un champ linéaire , montrer que ce champ est la superposition de deux champs circulaires d'intensités
. Etablir la relation entre et . Préciser les pulsations des deux champs circulaires.

16/ En déduire les expressions de dans le référentiel ( ) en présence de et de . Montrer que cette composante peut s'écrire . On explicitera ' et " en fonction de et . Donner les allures de ' et '' en fonction de . Montrer qu'à la résonance, il y a amplification de la susceptibilité.

Les techniques de détection de la RMN font généralement appel à une seule bobine dont l'axe est perpendiculaire au champ magnétique statique et dans laquelle apparaît un courant induit dû aux variations temporelles de l'aimantation transverse du système magnétique qu'elle contient.

Considérons une bobine cylindrique, de rayon et de longueur , constituée par un ensemble de spires jointives dont la densité par unité de longueur est n. L'axe de la bobine est confondu avec l'axe OX. On néglige les effets de bords c'est à dire qu'on adopte pour le champ magnétique créé par la bobine l'expression du champ B d'un solénoïde infini.

1/ Exprimer l'énergie du champ magnétique créé par la bobine parcourue par un courant constant en fonction de et . En déduire que la bobine possède une inductance propre qu'on exprimera en fonction de .

2/ On suppose maintenant que cette bobine est parcourue par un courant . Exprimer la puissance magnétique instantanée emmagasinée dans cette bobine en fonction de et .

3/ La bobine possède une résistance . Calculer la puissance instantanée dissipée par effet Joule.

4/ On définit le facteur de surtension Q de la bobine comme le rapport de la valeur maximale de la puissance instantanée emmagasinée dans la bobine sur celle de la puissance instantanée dissipée. Exprimer en fonction de et .

5/ Pour augmenter la sensibilité de la détection, cette bobine est montée en parallèle avec une capacité C ajustée telle que (on dit que " la bobine est accordée sur la capacité "). Montrer que si une force électromotrice est induite dans la bobine à une pulsation , il apparaît aux bornes du condensateur une différence de potentiel QE.

6/ Les caractéristiques de cette bobine sont données par:
. A la fréquence de Larmor pour un champ . On prendra . Calculer et .

Cette bobine est utilisée pour mesurer directement la relaxation de l'aimantation transverse. Dans cette technique connue sous le nom de "Free Induction Decay", la bobine n'est pas directement alimentée; elle n'est parcourue que par le courant induit associé à la force électromotrice crée par la variation de l'aimantation magnétique au sein du matériau.
Considérons le système magnétique de susceptibilité statique placé dans un champ magnétique et supposons que ce système ait été préparé par une " impulsion de ". La bobine contenant ce matériau est alors le siège d'une force électromotrice induite par l'aimantation créée au sein du matériau magnétique. En admettant que le champ magnétique au sein de la bobine est alors égal à , donner l'expression de cette f.e.m. en fonction de et . A partir des résultats obtenus à la question 12 de la partie , donner l'expression de .

Du fait que , on admet qu'on peut en première approximation traiter le facteur de décroissance exponentiel comme une constante et utiliser les résultats associés à un régime sinusoïdal de pulsation établis en D5.

8/ Sachant que le champ magnétique et que la susceptibilité magnétique est égale à , calculer les valeurs du facteur de qualité correspondant et de la tension maximale mesurée aux bornes du condensateur.

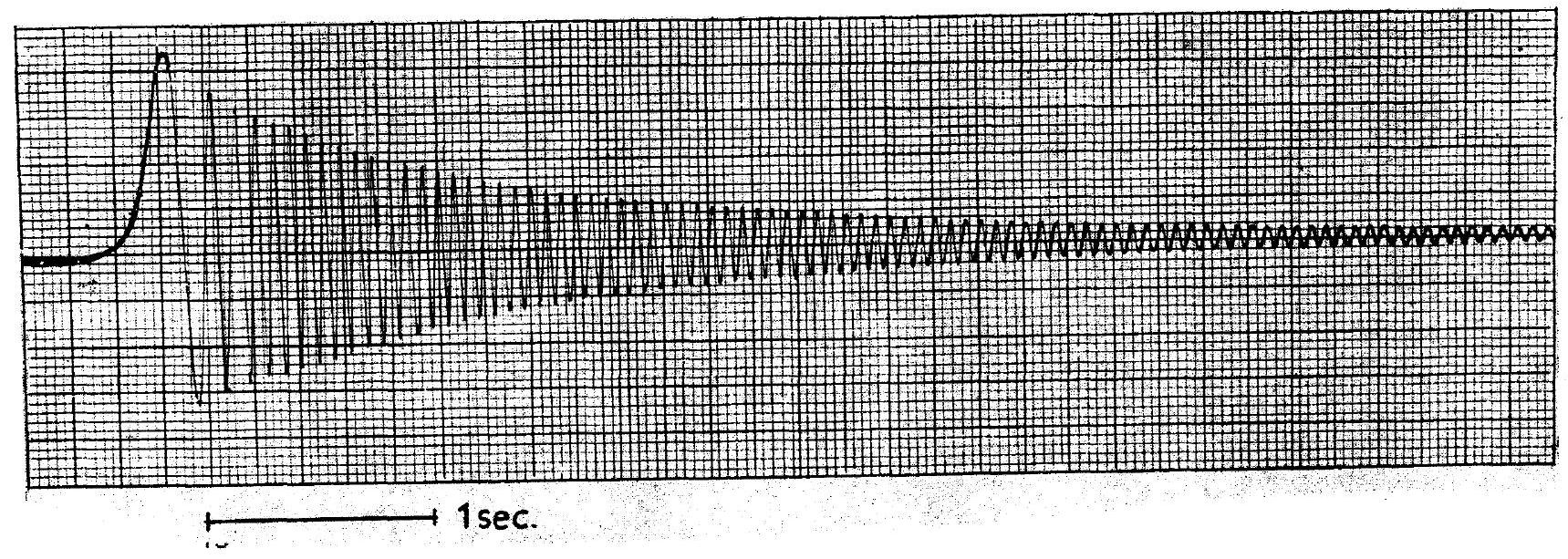
9/ La figure ci-dessous présente la décroissance du signal induit dans le cas de la RMN l'eau. A quel temps peut-on associer la décroissance de ce signal. En déduire l'ordre de grandeur de .