J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Informatique MP PC 2006

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2006
Filière
MP/PC
Matière
Info
X-ENS MP/PCX-ENS 2006MP/PC InfoInfo 2006
2025_08_29_c1a654decdafb16fbcfcg

Filière MP (groupes MPI et I)
Épreuve commune aux ENS de Paris, Lyon et Cachan

Filière PC (groupe I)Épreuve commune aux ENS de Paris et Lyon

INFORMATIQUE

Durée : 4 heures
L'usage de calculatrice est interdit
Ordre topologique et circuits booléens
Le sujet aborde la question du calcul des fonctions booléennes, en utilisant le modèle des circuits booléens.
La première partie introduit une notion fondamentale (ordre topologique sur un graphe sans cycle) et demande d'écrire ou d'étudier quelques algorithmes de base relatifs aux ordres topologiques. La seconde partie introduit les fonctions et les circuits booléens et aborde plusieurs questions relatives au calcul dans ce modèle, notamment d'expressivité. La troisième partie demande d'estimer des bornes de complexité, supérieures et inférieures.
Les seconde et troisième parties peuvent largement être abordées même si la première n'a pas été complètement résolue.

Définitions et conventions

Graphes. Un graphe (orienté) est un couple où est un ensemble fini (les sommets de ) et un sous-ensemble de (les arêtes de ). Si est un graphe à sommets, on identifiera à . Si est un ensemble, désignera son cardinal.
Si est une arête, on appelle son origine et on la note or ; on appelle l'extrémité de et on la note ex(a). Le sommet est dit fils de .
Un chemin de longueur est une suite d'arêtes telle que ex pour . On note l'ensemble de sommets . Ce chemin est un cycle si ex or .
Si est un sommet de , on appelle degré entrant de et on note in le nombre d'arêtes d'extrémité ; on appelle degré sortant de le nombre d'arêtes d'origine . Un sommet de degré entrant nul est appelé une entrée; un sommet de degré sortant nul est appelé une sortie; un sommet qui n'est pas une entrée est dit interne.
Structures de données et algorithmes. Dans la suite on manipulera des listes d'entiers, des tableaux d'entiers, de listes d'entiers, de booléens, ... Les indices d'un tableau de taille vont de 1 à ; la taille d'un tableau sera notée taille .
La liste vide est notée nil. Une liste non vide est formée d'un premier élément, noté tête , et de la liste formée par les autres éléments, notée queue . La primitive concat renvoie la liste formée en ajoutant en tête de . On note pour indiquer que l'élément appartient à la liste .
Vous pouvez utiliser le langage ou pseudo-langage de votre choix pour l'écriture de fonctions, en utilisant les structures de contrôle usuelles (Pour, Si, Tant que, . . .). La question 1.4. de la première partie illustre un choix possible. Certaines questions demandent de donner les principes d'un algorithme; pour ces questions, on ne demande pas d'écrire du pseudo-code, mais de décrire l'algorithme en français.
La complexité d'un algorithme désigne le nombre d'opérations élémentaires qu'il effectue : lecture ou écriture dans un tableau, tests, accès à la tête ou à la queue d'une liste, ... La création d'un tableau de taille a un coût . Si est une liste, le coût de l'affection est 1 . On ne cherchera pas à estimer les complexités exactement; on se contentera de donner un ordre de grandeur, en utilisant la notation asymptotique .

1 Ordre topologique et applications

Soit un graphe à sommets. Un ordre topologique sur est une bijection : telle que pour toute arête ( ) de ; l'ordre est représenté par le tableau . L'objectif de cette partie est de donner un algorithme pour déterminer un ordre topologique et quelques-unes de ses applications.

Question 1.1.

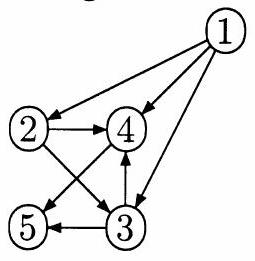
  1. Donner un ordre topologique pour chacun des graphes suivants, quand c'est possible.
  2. Montrer que admet un ordre topologique si et seulement s'il est sans cycle.
  3. Écrire une fonction Inverse(o) qui calcule le tableau . Quelle est sa complexité?
Le graphe est donné par listes d'adjacence, c'est-à-dire par un tableau , de taille , de listes d'entiers, tel que si et seulement si est une arête de . De plus, chaque liste est sans répétition.

Question 1.2.

  1. Écrire une fonction Parents qui renvoie un tableau , de taille , contenant des listes d'entiers, tel que si et seulement si est une arête de (chaque liste sera sans répétition). Quelle est sa complexité?
  2. Donner les principes d'un algorithme qui renvoie le tableau de taille donnant le degré entrant de chaque sommet et d'un algorithme qui renvoie la liste des entrées de . Quelle est la complexité de ces algorithmes?
  3. En utilisant les algorithmes précédents, donner les principes d'un algorithme qui calcule un ordre topologique sur (s'il existe), en complexité .
Dans toute la fin de cette partie, on suppose sans cycle. Si est un ordre topologique sur , on dit qu'une liste d'éléments distincts de est triée selon l'ordre o si, soit est vide, soit est réduite à un élément, soit tête tête(queue et queue est triée selon l'ordre .
Question 1.3. Soit un ordre topologique sur . Écrire une fonction TriSuccesseurs , de complexité , qui trie les listes d'adjacence contenues dans le tableau selon l'ordre .
La fermeture réflexive transitive de est le graphe tel que ( ) appartient à si et seulement s'il existe un chemin dans tel que et , ou bien si . L'objectif de la fin de cette partie est de calculer cette fermeture. Au vu des questions précédentes, quitte à renuméroter les sommets, on suppose désormais que l'application forme un ordre topologique sur et que les listes d'adjacence du tableau sont données triées selon cet ordre.
Question 1.4. On étudie dans cette question l'algorithme de la figure 1, page 4. Il prend en entrée le tableau des listes d'adjacence triées.
  1. Pour le graphe suivant, donner les valeurs de et à chaque entrée dans la boucle des lignes 2-27, ainsi qu'à la fin de l'algorithme.
  2. Montrer qu'à l'issue de cet algorithme, le tableau fournit une description de par listes d'adjacence.
  3. CréerTableau faux, CréerTableau nil,
    ( et sont des tableaux, respectivement de booléens et de listes d'entiers, respectivement initialisés à faux et nil, et de taille )
  4. Pour allant de à 1 Faire
  5. , nil
  6. vrai
  8. Tant que nil Faire
  9. tête
  10. queue
  11. Si faux Faire
  13. Tant que nil Faire
  14. tête
  15. queue
  16. Si faux Faire
  17. vrai
  19. Fin Si
  20. Fin Tant que
  21. Fin Si
  22. Fin Tant que
  24. Tant que nil Faire
  25. tête
  26. queue
  27. faux
  28. Fin Tant que
  29. Fin Pour
  30. Renvoyer
Fig. 1 - Algorithme de la question 1.4.
3. Soit le sous-ensemble des arêtes de tel que si et seulement si et s'il n'existe pas de chemin de longueur supérieure ou égale à 2 entre et dans . Montrer que le nombre de sommets internes de est borné par , que est borné par et estimer la complexité de l'algorithme étudié en fonction de et .
Indication : on pourra montrer que les lignes 10 à 18 sont exécutées si et seulement si ( ) est dans .
4. La grandeur est toujours inférieure à . Est-il possible de la majorer par une fonction de type , pour un ?
Une chaîne est un ensemble de sommets de soit réduit à un élément, soit de la forme , pour un chemin .
Question 1.5. On étudie pour conclure cette partie un second algorithme de fermeture réflexive transitive.
  1. Écrire une fonction Chaines qui calcule une partition de en chaînes, avec la propriété (de minimalité) suivante : pour toutes chaînes et calculées par cette fonction, n'est pas une chaîne.
    Cette fonction renverra un tableau de listes d'entiers triées en ordre croissant (c'est-àdire selon l'ordre topologique et sans répétition. Estimer sa complexité.
  2. Soit une partition de en chaînes, donnée par un tableau de listes d'entiers sans répétition, triées en ordre croissant. Pour et , on définit si cet ensemble n'est pas vide, et sinon. Enfin, on note le tableau de taille tel que est l'unique indice pour lequel .
    (a) Montrer que si et que, sinon, si cet ensemble n'est pas vide.
    (b) Soit et soit et . Si est vide, on pose ; sinon, on pose . Montrer que si et seulement si .
    (c) Écrire une fonction calculant les valeurs en complexité .
  3. Donner les principes d'un second algorithme qui calcule la fermeture réflexive transitive de et estimer sa complexité. La sortie sera présentée sous la forme d'un tableau de listes d'adjacence. On ne demande pas que ces listes soient triées.
    Remarque : si le graphe est aléatoire, au sens où chaque arête ( ) est présente avec une probabilité fixée, ces idées mènent à un algorithme de complexité moyenne , contre pour celui de la question 1.4.

2 Fonctions booléennes et circuits booléens

Définitions. Pour , on note l'ensemble des fonctions et on pose est l'ensemble des fonctions booléennes. On note la fonction ou, la fonction et, la fonction ou exclusif et la fonction non, définies ci-dessous :
0 0 0
0 1 1
1 0 1
1 1 1
0 0 0
0 1 0
1 0 0
1 1 1
0 0 0
0 1 1
1 0 1
1 1 0
0 1
1 0
On définit également les fonctions constantes et qui valent respectivement 0 et 1 .
Pour et dans , on note si pour tout . Pour un sous-ensemble non vide de , on note la valeur (cette valeur est bien définie, en vertu de l'associativité et de la commutativité de ) ; si est vide, vaut 0 . Finalement, une fonction est dite :
  • monotone si implique pour tous dans ;
  • auto-adjointe si pour tout ( ) dans ;
  • affine s'il existe et tels que pour tout dans .
    Pour , on note si et sinon. Pour , on dira alors que est de type
  • ET s'il existe tels que pour tous dans ;
  • XOR s'il existe tel que pour tous dans .

Question 2.1.

  1. Parmi toutes les fonctions de , quelles sont celles qui sont de type ET? De type XOR? Des deux types simultanément?
  2. Montrer qu'une fonction de type XOR est affine. Y a-t-il d'autres fonctions affines dans ?
  3. Que vaut pour ? Que vaut pour ?
Soient et dans . On dit que est une spécialisation de s'il existe un sous-ensemble et des constantes satisfaisant les conditions suivantes : pour tout , avec si et sinon. On dit que fixe les variables , pour .

Question 2.2.

  1. Montrer par récurrence sur que si n'est pas affine, il existe une spécialisation de qui fixe toutes les variables sauf deux d'entre elles, et , et telle que , pour des constantes dans .
  2. Pour , montrer que si n'est pas monotone, il existe une spécialisation de qui fixe toutes les variables sauf une d'entre elles, , et telle que .
Soit un ensemble fini de fonctions booléennes. Un circuit sur est la donnée
  • d'un graphe sans cycle . On suppose que forme un ordre topologique sur et que les entrées sont numérotées de 1 à .
  • d'une fonction telle que si in et, si est une entrée, pour .
    On associe à un circuit à entrées une application définie ainsi :
  • pour toute entrée de ;
  • si est un sommet interne, et si sont les arêtes d'extrémité , avec , on définit par pour tout .
    Intuitivement, au sommet , on applique la fonction aux valeurs calculées dans les sommets précédents. On dit que le sommet calcule la fonction . Une fonction est calculée par un circuit sur s'il existe un sommet du graphe associé tel que .
    La taille d'un circuit est le nombre de sommets internes de (c'est-à-dire de sommets qui ne sont pas des entrées). La profondeur d'un circuit est la longueur du plus long chemin dans .

Question 2.3.

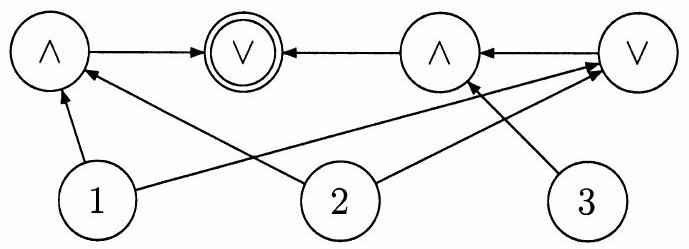
  1. Dans l'exemple suivant, indiquer quelle fonction est calculée par le sommet entouré deux fois (on ne donne que la numérotation des noeuds d'entrée, aucune ambiguïté n'étant possible).
  2. Pour dans , on définit par si et seulement si . Montrer que peut être calculée par un circuit sur de taille et de profondeur , en utilisant une approche de type "diviser pour régner".
  3. En déduire que pour tout , toute fonction dans peut être calculée par un circuit sur . Quelle est la taille de ce circuit? Sa profondeur?
Question 2.4. Un ensemble est complet si toute fonction de peut être calculée par un circuit sur .
  1. Réinterpréter le résultat de la question 2.3.3 en termes d'ensemble complet. Donner un ensemble complet, minimal au sens de l'inclusion.
  2. On va caractériser les ensembles complets. Considérons les conditions suivantes:
    (i) il existe telle que (ici, signifie que tous les arguments de sont mis à 0 );
    (ii) il existe telle que (même remarque que ci-dessus);
    (iii) il existe non monotone;
    (iv) il existe non auto-adjointe;
    (v) il existe non affine;
    (vi) il existe un circuit sur à une entrée et un sommet interne du graphe associé tels que calcule la fonction identité .
    (a) Montrer que ces conditions sont nécessaires.
    (b) Réciproquement, on suppose ces conditions satisfaites.
  • Montrer en utilisant (i)-(iii) et (vi) qu'on peut calculer la fonction par un circuit sur .
  • Montrer en utilisant (iv) et (vi) qu'on peut calculer les fonctions et par des circuits sur .
  • Montrer en utilisant (v) qu'on peut calculer par un circuit sur une fonction de type ET. Conclure.

3 Bornes supérieures et bornes inférieures

Dans toute cette partie, on pose : tous les sommets des graphes considérés sont donc de degré entrant 0,1 ou 2 . La première question traite un exemple de borne supérieure sur le coût du calcul de certaines fonctions; la fin du problème aborde des questions de bornes inférieures.
Une matrice booléenne de taille est la donnée de valeurs dans . Si et sont deux telles matrices, on note la matrice booléenne de taille définie par avec
On note par ailleurs la matrice booléenne de taille définie par avec . Pour , on définit les puissances par récurrence : est la matrice , qui a toute ses entrées nulles, à l'exception de la diagonale , remplie par des 1 ; pour , on pose .

Question 3.1.

  1. Soit un graphe à sommets. Sa matrice d'adjacence est la matrice booléenne de taille telle que si et seulement si . Caractériser les éléments de en fonction des chemins dans .
  2. Pour , soit la fonction qui à la matrice d'adjacence d'un graphe , de taille , associe 1 si et seulement si ou s'il existe un chemin de à dans . Montrer que pour tous peut se calculer par un circuit sur de taille et de profondeur .
Pour une fonction booléenne , on note la taille minimale d'un circuit qui calcule sur , si un tel circuit existe (sinon, on pose ). Un circuit qui calcule sur est optimal pour si sa taille vaut .

Question 3.2.

  1. Soit un graphe sans cycle, ayant entrées, sorties (toutes distinctes des entrées) et sommets (internes ou non) de degré sortant supérieur ou égal à 2 . Montrer que si tout sommet interne de a un degré entrant inférieur ou égal à 2 , alors contient au moins sommets internes.
    Indication : on pourra compter le nombre d'arêtes de deux façons différentes.
  2. Soit dans et soit un circuit sur qui calcule . Montrer les assertions suivantes :
    (a) Si est optimal pour , alors :
  • si et sont deux sommets distincts de ;
  • il existe un unique sommet de tel que et c'est une sortie de ;
  • il existe au plus un sommet interne de qui soit une sortie.
    (b) On suppose que n'est ni constante, ni de la forme . On suppose également que a sommets internes pour lesquels est dans ou n'est ni de type ET ni de type XOR. Montrer qu'alors est plus petit que la taille de .
Question 3.3. Soit . Pour dans , on note l'entier . Posant , on définit la fonction par
Le but de cette question est de donner une borne inférieure sur . Pour cela, pour , on définit par
de cardinal tel que .
Soit dans , avec dans , soit un circuit sur qui calcule optimalement et soit tel que est dans un ensemble associé à selon la définition ci-avant. En fixant , construire une fonction dans telle que . En déduire que .
Indication : on pourra distinguer selon le degré sortant de l'entrée correspondant à . Si ce degré est 1, on discutera selon la nature du fils et on utilisera la question 2.1.3.
Question 3.4. Soit dans , pour . On suppose qu'il existe de cardinal au moins 2, satisfaisant la propriété suivante : pour tous , avec , il existe des spécialisations et de qui fixent toutes les variables sauf et , et des constantes telles que
  1. Soit un circuit optimal qui calcule sur . Soient et dans , avec , et des chemins de l'entrée (respectivement l'entrée ) à , l'unique sommet de qui calcule . On note le sommet de plus petit indice commun aux deux ensembles et . Montrer qu'il existe, dans ou dans , un sommet d'indice strictement plus petit que celui de et de degré sortant supérieur ou égal à 2 .
  2. Montrer qu'il existe éléments tels que, pour tout , tout chemin de à contient un sommet de degré sortant au moins 2 . Montrer de plus qu'on peut choisir ces sommets de sorte qu'ils soient tous distincts. En déduire l'inégalité .
  3. Pour , que dire de la fonction définie par si et seulement si ?
Question 3.5. Montrer que pour assez grand, il existe telle que . Indication : on pourra compter le nombre d'éléments dans et utiliser une majoration sur le nombre de circuits de taille à entrées qu'on peut construire sur .
ENS Informatique MP PC 2006 - Version Web LaTeX | WikiPrépa | WikiPrépa