J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Physique C PC 2019

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2019
Filière
PC
Matière
Physique
X-ENS PCX-ENS 2019PC PhysiquePhysique 2019
2025_09_04_cd9f295dacbccea1db1fg

ECOLES NORMALES SUPERIEURES CONCOURS D'ADMISSION 2019

MERCREDI 24 AVRIL 2019-8h00-14h00 FILIERE PC - Epreuve n

COMPOSITION DE PHYSIQUE C
(U)

Détection et caractérisation des exoplanètes

Il y a trente ans, en 1989, était annoncée la première détection d'une exoplanète, c'est-à-dire une planète en orbite autour d'une étoile autre que le Soleil, en l'occurrence l'étoile , sous-géante orange et membre principal d'un système binaire situé à quelques 45 années-lumière de la Terre, dans la constellation de Céphée. Si l'existence de cette exoplanète ne fut confirmée définitivement qu'en 2002, on considère généralement que cette découverte fut la première du genre. À ce titre, cette planète fut choisie en 2014 pour recevoir un nom au terme du concours NameExo Worlds organisé par l'Union Astronomique Internationale. En décembre 2015, elle fut baptisée Tadmor, autre nom de la cité de Palmyre (Syrie).
Cette découverte ouvrit la voie à une moisson toujours plus importante d'objets exoplanétaires, jalonnée par plusieurs détections notables :
  • 1992 : première détection confirmée d'exoplanètes, autour du pulsar B1257+12 (Wolszczan et al.)
  • 1995 : première planète confirmée autour d'une étoile de la séquence principale, c'est-à-dire semblable au Soleil, 51Peg b, ultérieurement nommée Dimidium (Mayor & Queloz)
  • 1999 : détection d'un système composé de plusieurs planètes, en l'occurrence quatre, autour d'une étoile de la séquence principale, And.
  • 1999 : détection d'une exoplanète par la méthode des transits en sus de la méthode des vitesses radiales, HD209458 b, surnommée Osiris. Cet objet a également fourni la première détection d'une atmosphère exoplanétaire, en 2001.
  • 2004 : observation d'une exoplanète par imagerie directe infrarouge, 2M1207b, en orbite autour d'une naine brune (Chauvin et al.).
  • 2006 : détection d'une exoplanète par effet de microlentille gravitationnelle, OGLE-2005-BLG-390L b.
  • 2007 : découverte d'exoplanètes dans la zone d'habitabilité, c'est-à-dire potentiellement susceptibles de receler de l'eau sous forme liquide, dans le système Gliese581 (von Bloh et al.).
  • 2008 : détection d'une signature de molécule organique, en l'occurrence du méthane, dans une atmosphère exoplanétaire, celle de HD189733b.
  • 2008 : mesure du mouvement orbital de plusieurs planètes du système HR8799 par imagerie directe.
  • 2014 : détection de 715 exoplanètes, autour de 305 étoiles, par la mission spatiale Kepler.
  • 2016 : découverte d'une exoplanète de masse comparable à la Terre, dans la zone d'habitabilité de Proxima Centauri, plus proche voisine du Soleil.
  • 2017 : détection d'un système, TRAPPIST-1, composé de sept planètes de masses comparables à la Terre et situées dans la zone d'habitabilité de leur étoile.
Au janvier 2019, on compte 2946 systèmes exoplanétaires confirmés, dont 650 multiples, pour un total de 3947 exoplanètes.
Nous allons nous intéresser dans ce problème à quelques uns des aspects de la physique mise en jeu pour la détection et la caractérisation des exoplanètes. L'information permettant de mettre en évidence ces exoplanètes étant de nature électromagnétique, la première partie introduit les grandeurs physiques utiles dans le traitement des questions de rayonnement. La deuxième partie traite de la méthode des vitesses radiales, qui a permis les premières découvertes. La troisième partie traite de la méthode des transits, mise à l'honneur par la mission spatiale Kepler. Si la problématique est commune aux différentes parties du problème, celles-ci sont néanmoins très largement indépendantes. On précise que dans tout le problème, les notations en gras représentent des vecteurs. En particulier, la notation rot désigne le vecteur rotationnel du vecteur , la notation en désignant la divergence. La notation désigne le produit vectoriel des deux vecteurs et , et la notation leur produit scalaire. La calculatrice n'étant pas autorisée, on fera les applications numériques à la main, en utilisant les valeurs indiquées dans le formulaire ci-après. Pour certaines de ces applications, on pourra donner une estimation grossière. Les candidats sont invités à ne pas négliger ces questions.

Formulaire

Vitesse de la lumière dans le vide
Constante de Planck
Constante de Boltzmann
Constante de la gravitation
Charge élémentaire
Nombre d'Avogadro
Masse de l'électron
Masse du proton
Permittivité du vide
Perméabilité du vide
Masse du Soleil
Rayon du Soleil
Température de surface du Soleil
Rayon de la Terre
Masse de la Terre
Distance moyenne Soleil-Terre [unité astronomique]
Rayon de Jupiter
Masse de Jupiter
Distance moyenne Soleil-Jupiter

I. Préambule : quelques éléments de physique du rayonnement

Au cours de ce problème, on considère des grandeurs physiques liées à l'observation du rayonnement des étoiles et des planètes. Ce préambule permet de poser les notations et les relations fondamentales de ce domaine, en partant des lois de l'électromagnétisme dans le vide. On rappelle que celles-ci sont fondées classiquement sur l'ensemble des quatre équations de Maxwell :
Les objets qu'on sera amené à considérer étant très lointains, on pourra supposer que les ondes électromagnétiques qui nous en parviennent sont planes et progressives. On considère dans cette partie une telle onde se propageant dans une direction repérée par un vecteur unitaire , et on rappelle que le champ électrique et le champ magnétique de cette onde sont reliés par
où est la célérité de la lumière dans le vide. Dans les questions Q1 à Q4, l'onde plane progressive est de plus supposée monochromatique.
Q1. Représenter schématiquement les vecteurs et en un point de l'espace et à un instant donné.
Q2. Montrer, à partir des équations de Maxwell dans le vide, qu'on peut établir une équation de conservation de l'énergie du champ électromagnétique sous la forme
Dans cette équation, appelée identité de Poynting, est la densité volumique d'énergie électromagnétique et est le vecteur de Poynting. On a noté le module du vecteur champ électrique et celui du vecteur champ magnétique.
Q3. Montrer que le vecteur de Poynting s'écrit et expliciter son module .
La formule de Green-Ostrogradsky permet d'écrire l'identité de Poynting sous une forme intégrale, en considérant un volume fixe, dont on note la surface frontière fermée . En posant avec le vecteur normal à la surface dirigé vers l'extérieur de , et l'élément de volume, on montre alors que
∯é
Cette expression permet d'interpréter le flux du vecteur de Poynting apparaissant dans le membre de droite comme la puissance électromagnétique traversant la surface .
Q4. On considère une petite surface perpendiculaire à la direction de propagation . À l'aide d'un schéma, justifier que l'énergie électromagnétique traversant cette surface pendant un petit temps s'écrit . Justifier à l'aide d'un second schéma que si la petite surface est inclinée d'un angle par rapport à la direction de propagation, cette expression devient .
On considère maintenant un rayonnement constitué d'un ensemble d'ondes planes progressives, avec une répartition spectrale continue en fonction de la longueur d'onde , se propageant toutes dans la même direction. On considère que ces différentes ondes n'interfèrent pas entre elles et on peut donc traiter le rayonnement de longueur d'onde à près comme une onde plane progressive monochromatique.
Q5. Dans une approche corpusculaire du rayonnement, l'énergie électromagnétique est donc portée par des photons de différentes longueurs d'onde , et l'on rappelle que l'énergie d'un photon est liée à sa longueur d'onde par . On note le nombre de photons par unité de volume dont la longueur d'onde est comprise entre et , et la densité volumique d'énergie du champ électromagnétique dans cet intervalle de longueur d'onde. Exprimer , puis , en fonction de .
Q6. En déduire que si l'on ne s'intéresse qu'à l'énergie électromagnétique traversant la surface pendant et portée par des photons de longueur d'onde comprise entre et , on peut l'écrire
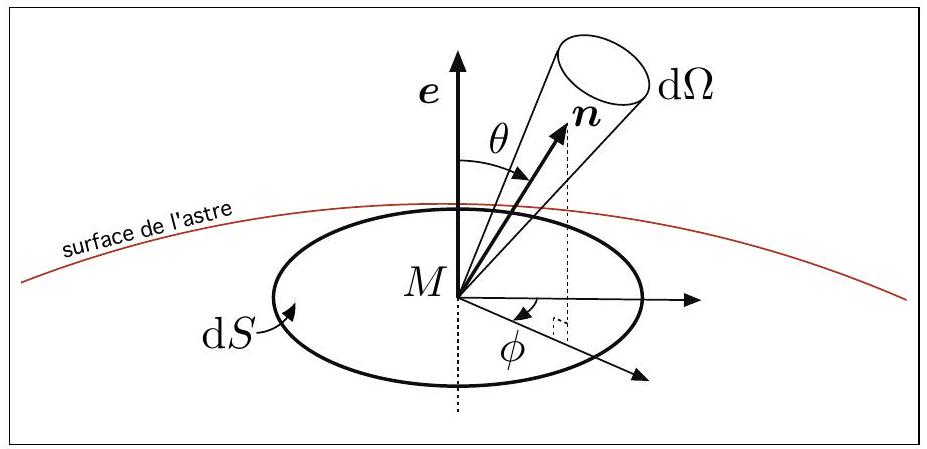
Jusqu'à présent, nous avons considéré que la direction de propagation des photons était parfaitement déterminée. En réalité, il convient de tenir compte du fait que cette direction de propagation n'est pas à valeurs discrètes, mais peut varier continûment. Il faut donc exhiber un "élément d'intégration" sur les directions, semblable à ce que peut être pour le temps ou pour la longueur d'onde. Comme on repère la direction de propagation par le couple d'angles indiqué sur la Fig. 1, avec et , cet élément d'intégration sur les directions doit faire intervenir les variations infinitésimales et . On admettra qu'il s'agit de l'angle solide élémentaire .
Figure 1 - Définition des angles et , et de l'élément d'angle solide .
On sera amené dans la suite à considérer des éléments à la surface d'astres (planètes et étoiles). La Fig. 1 indique comment orienter la normale à , à savoir de l'intérieur de l'astre vers son extérieur.
Q7. Montrer que l'angle solide correspondant à l'ensemble des directions de l'espace est .
On introduit la quantité de telle sorte que le nombre de photons par unité de volume dont la longueur d'onde est comprise entre et et dont la direction de propagation est à près soit . L'énergie portée par ces photons et traversant la surface pendant s'écrit alors
ce qui définit la quantité , appelée intensité spécifique ou encore brillance. La propriété fondamentale de l'intensité spécifique est qu'elle se conserve lors de la propagation de la lumière dans le vide. Ainsi, si l'on suit le parcours d'un rayon lumineux de la surface d'une source jusqu'au détecteur utilisé par un astronome, elle est identique au niveau de la source et au niveau du détecteur.
Q8. Exprimer en fonction de .
Q9. La densité spectrale de flux, notée , est la puissance électromagnétique, par intervalle de longueur d'onde et par unité de surface, intégrée sur toutes les directions, à savoir
Exprimer comme une intégrale sur et faisant intervenir l'intensité spécifique .
Le rayonnement émis par les corps que nous considérerons dans ce problème peut être modélisé par celui dit d'un corps noir à la température , cette température étant celle de la surface de l'étoile ou de la planète. Avec les notations de la Fig. 1, on supposera que l'intensité spécifique entrante dans l'astre est nulle, soit pour , et que l'intensité spécifique sortante de l'astre ( ) est indépendante de et et prend la forme
qu'on appelle fonction de Planck.
Q10. Montrer que la densité spectrale de flux sortant d'un élément de surface du corps est , puis que le flux sortant total, c'est-à-dire la densité spectrale de flux sortant intégrée sur toutes les longueurs d'onde, est donné par la loi de Stefan-Boltzmann, , où est la constante de Stefan, qu'on exprimera en fonction de constantes physiques fondamentales.
Q11. La luminosité bolométrique d'un astre est la puissance lumineuse totale qu'il émet. Pour un corps noir sphérique, exprimer cette luminosité en fonction du rayon et de la température du corps. Exprimer également la luminosité spectrale , qui est la puissance émise par intervalle de longueur d'onde, de sorte que
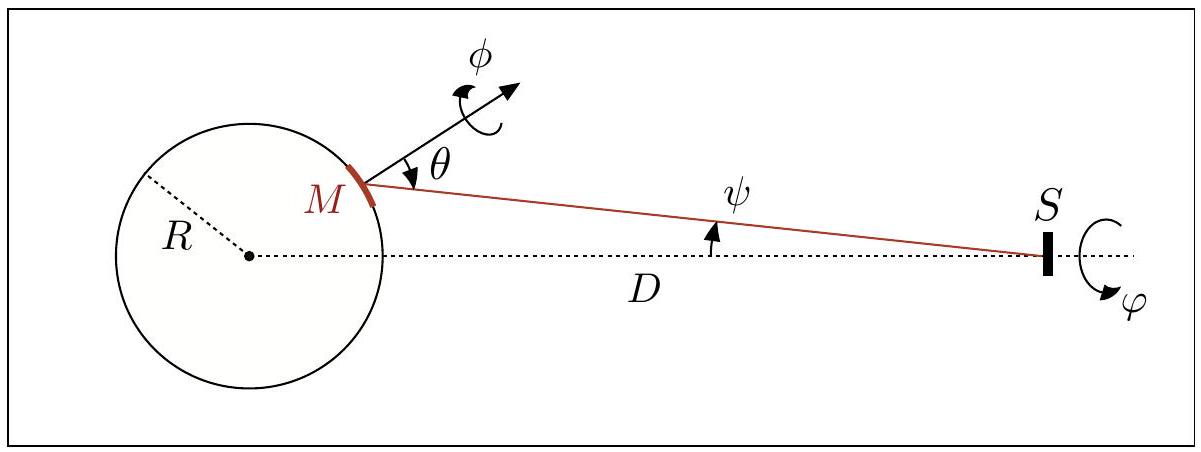
Figure 2 - Détection du rayonnement d'un corps céleste.
Q12. On sera amené, dans la partie III, à considérer la puissance reçue par un détecteur de surface , situé à une distance du corps noir et placé perpendiculairement à la ligne de visée, laquelle est la droite joignant le centre du système observé à l'observateur (Fig. 2). Calculer , en raisonnant sur la puissance lumineuse par unité de surface à la distance . Que vaut la puissance spectrale reçue par intervalle de longueur d'onde au niveau du détecteur?

II. Détection par la méthode des vitesses radiales

La première méthode fiable de détection des exoplanètes repose sur l'exploitation du fait que l'interaction gravitationnelle entre une étoile et une planète a non seulement un impact sur le mouvement de la planète, mais aussi, et réciproquement, sur le mouvement de l'étoile. C'est la mesure de ce mouvement stellaire, et plus précisément de la vitesse radiale de l'étoile, c'est-à-dire de la composante de sa vitesse projetée sur la ligne de visée la reliant à l'observateur, qui permet de détecter l'existence d'une planète en orbite autour de cette étoile. Dans cette partie, nous allons d'abord établir l'expression de cette vitesse radiale, en fonction des différents paramètres physiques du problème. Nous étudierons ensuite le principe de fonctionnement d'un instrument dédié à sa mesure.

II. 1 - Réduction du problème de Kepler à deux corps

On considère le problème suivant, dit de Kepler : un système constitué d'une étoile , de masse , et d'une planète , de masse , toutes deux assimilées à des objets ponctuels, en interaction gravitationnelle. On fait l'hypothèse que ce système est isolé, et on se place dans un référentiel ( ), supposé Galiléen, attaché à un observateur terrestre . On note le rayon vecteur liant cet observateur à l'étoile, celui le liant à la planète, et le rayon vecteur liant l'étoile à la planète.
Q13. Écrire les équations du mouvement de chacun des deux corps dans .
Q14. On note le centre de masse du système. Déterminer son rayon vecteur en fonction des paramètres du problème.
Q15. Montrer que le mouvement du centre de masse est rectiligne uniforme. Dans toute la suite du problème, on supposera, sans perte de généralité, que est fixe par rapport à , soit . Le référentiel barycentrique ( ) est alors confondu avec ( ).
Q16. Exprimer les vecteurs et en fonction de , et des masses et , puis les vecteurs position et des deux astres par rapport au centre de masse .
Q17. Montrer que le mouvement relatif de par rapport à obéit à l'équation
où est la masse réduite, et où l'on explicitera l'expression de la force . On pourra poser pour désigner la masse totale du système. Une fois qu'on aura résolu le mouvement relatif décrit par l'équation (10), ce qu'on fera dans la partie II.2, comment s'en déduiront les trajectoires de et dans le référentiel ( ) ? Pourquoi dit-on que l'on a ainsi réduit le problème de Kepler?

II. 2 - Résolution du mouvement relatif

On considère donc le mouvement , décrit par l'équation (10), d'une particule ponctuelle fictive de masse , soumise à la force centrale , dans le référentiel ( ). Le vecteur est le vecteur unitaire radial dirigé vers l'extérieur du centre de force, et . On note le vecteur vitesse de .
Q18. Montrer que la force dérive d'une énergie potentielle
Q19. Montrer que le moment cinétique de par rapport au centre de force se conserve. Quelle conséquence peut-on en tirer quant à la trajectoire de ?
Q20. On prend comme coordonnées un système cylindrique ( ) dans lequel l'axe est celui portant le moment cinétique, . Exprimer en fonction de ces coordonnées.
Q21. Montrer que l'énergie mécanique de , qui se conserve, peut se mettre sous la forme
où est une énergie potentielle effective qu'on exprimera en fonction de , et .
Q22. Représenter graphiquement l'énergie potentielle effective . Discuter la nature des trajectoires en fonction de la valeur de . En particulier, quelle est la condition sur pour que la trajectoire de la particule soit bornée? On se place dans ce cas de figure pour le reste du problème.
Q23. En posant , montrer que les distances minimale (périastre) et maximale (apoastre) entre le centre de force et la particule fictive peuvent se mettre sous la forme
On exprimera les paramètres et en fonction de et . Quelles sont les bornes des valeurs possibles de ?
Q24. Montrer, à partir de l'équation énergétique (12), que si l'on considère la trajectoire de par le biais de plutôt que par celui du couple , on aboutit à une équation de la forme
On précisera les constantes et en fonction de et . En déduire que obéit à une équation d'oscillateur harmonique. En posant comme condition "initiale" que passe au périastre lorsque , en déduire que la trajectoire a pour équation
qui est celle d'une ellipse. Les coefficients et sont respectivement le paramètre et l'excentricité de cette ellipse.
Q25. On se place désormais dans le cas d'un mouvement circulaire. Que vaut l'excentricité dans ce cas? Calculer le rayon de cette trajectoire, en fonction de et . Que peut-on dire du module de la vitesse de la particule fictive ? Calculer sa valeur , en fonction des mêmes paramètres que . Montrer que l'angle évolue avec le temps selon , en explicitant la pulsation .
Q26. À partir du système de coordonnées cylindriques ( ) de la question Q20, on peut aussi définir un système de coordonnées cartésiennes ( ), tel que et . Exprimer le mouvement de la particule fictive en prenant comme origine des temps un instant où et , afin de fixer . Montrer que . Comment s'appelle cette relation?

II. 3 - Cinématique de l'étoile en présence d'une planète

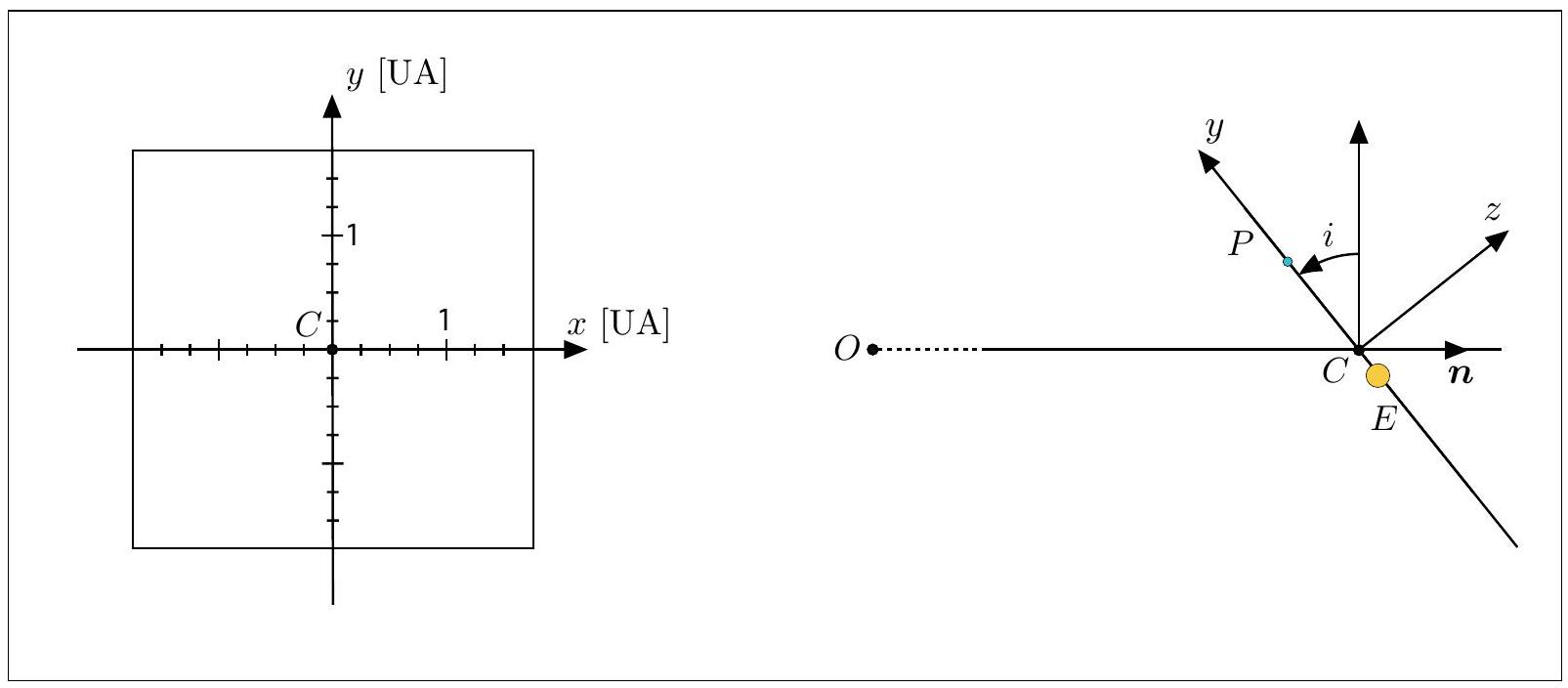
Q27. Maintenant que nous avons déterminé le mouvement de la particule fictive , on revient à la situation considérée initialement, pour laquelle une étoile de masse et une planète de masse sont en interaction gravitationnelle. On rappelle qu'on se place dans le cas d'un mouvement circulaire. En utilisant les résultats de Q16 et Q26, exprimer les lois du mouvement et des deux astres par rapport au centre de masse supposé fixe. On posera .
Figure 3 - Gauche : Représentation du plan de la trajectoire - Droite : Définition de l'angle d'inclinaison du plan de la trajectoire par rapport à la ligne de visée. Le vecteur unitaire définit la ligne de visée vers le centre de masse du système.
Q28. Reproduire le schéma de gauche de la Fig. 3 et y tracer les trajectoires de la particule fictive et des deux astres et , dans le cas UA et . On représentera également les positions de , et à un instant donné.
Q29. Le plan des trajectoires de et forme un angle , compris entre et , avec le plan du ciel (c'est-à-dire le plan perpendiculaire à la ligne de visée ), comme indiqué sur le schéma de droite de la Fig. 3. Calculer la composante de la vitesse de l'étoile le long de la ligne de visée. Cette composante est appelée vitesse radiale.
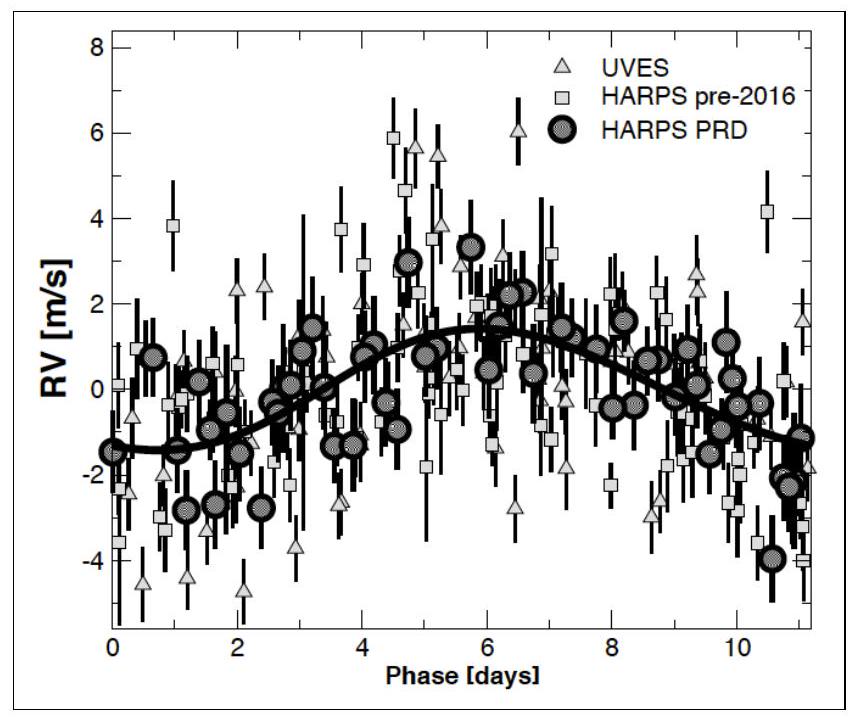
Q30. Tracer l'allure de la vitesse radiale en fonction du temps. C'est ce signal que l'on détecte par spectroscopie Doppler, comme on le verra dans la suite. Montrer que la mesure de l'amplitude et de la période de la variation de cette vitesse radiale en fonction du temps permet de contraindre la masse de la planète en orbite autour de l'étoile, si l'on connaît la masse de cette dernière et l'angle de l'orbite planétaire. On fera apparaître la fonction de masse du système, définie par
Figure 4 - Mesures de la vitesse radiale de l'étoile Proxima Centauri avec les instruments HARPS et UVES de l'ESO. Les données (représentées par les cercles, carrés et triangles) ont été prises au cours de 16 ans d'observations, et compilées pour faire ressortir, par ajustement (courbe en traits pleins), le signal périodique associé à la présence d'une planète (Anglada-Escudé et al., 2016).
Q31. Simplifier le résultat obtenu dans le cas où la masse de la planète est très petite devant celle de l'étoile. Donner alors une estimation de la masse minimale de la planète. Pour quelle inclinaison de l'orbite est-il plus facile de détecter la présence d'une planète en orbite autour de l'étoile? Vaut-il mieux que l'étoile soit de faible masse ou de grande masse?
Q32. La Fig. 4, tirée de Anglada-Escudé et al. (2016) représente les mesures de la vitesse radiale de l'étoile Proxima Centauri effectuées à l'aide de deux instruments, HARPS et UVES, de l'Observatoire Européen Austral (ESO), au Chili. Estimer la période et l'amplitude du signal, et en déduire une estimation (grossière) de la masse minimale de la planète Proxima Centauri b. La masse de l'étoile Proxima Centauri est de , soit 0,12 masse solaire.

II. 4 - Principe de la spectroscopie Doppler

Le principe de la mesure des vitesses radiales des étoiles, et de leurs variations au cours du temps qui signalent la présence d'une planète, repose sur l'effet Doppler-Fizeau. Celui-ci stipule que la longueur d'onde d'un signal en provenance d'une source , telle que mesurée par un observateur , diffère de la longueur d'onde du signal dans le référentiel de la source si celle-ci est en mouvement par rapport à . En notant la projection de la vitesse de la source sur la ligne de visée, on a
où est la célérité de l'onde (électromagnétique dans notre cas). La convention utilisée est que si la source s'éloigne de l'observateur. On précise que la mesure des vitesses radiales se fait en mesurant le décalage au cours du temps de raies spectrales en absorption dans le spectre de l'étoile.
Q33. Montrer que si la vitesse est faible ( ), alors le décalage en longueur d'onde vérifie
On se placera dans cette approximation classique, c'est-à-dire non-relativiste, pour le reste du problème.
Q34. Citer un exemple de cet effet dans un autre domaine de la physique que l'électromagnétisme.
Les spectromètres sont de manière générale des instruments permettant de disperser, c'est-à-dire de séparer spatialement des vibrations lumineuses de différentes longueurs d'onde présentes dans un faisceau. Leur caractéristique fondamentale est le pouvoir de résolution
où est le plus petit écart entre longueurs d'onde qui puisse être distingué au voisinage de .
Q35. Étant donné un spectromètre dont le pouvoir de résolution est , quelle doit être l'amplitude de la vitesse radiale de l'étoile pour détecter la présence d'une exoplanète? Montrer que le pouvoir de résolution du spectromètre utilisé pour détecter la planète Proxima Centauri b (Fig. 4) doit satisfaire
L'instrument en question, HARPS ( igh A ccuracy adial velocity lanet earcher ), est un spectromètre à réseau de type échelle installé au foyer du télescope de de diamètre de l'ESO, à l'Observatoire de La Silla, au Chili. On discute dans la suite de cette partie du principe de cet instrument.

II. 5 - Étude d'un réseau en réflexion

L'élément de base de l'instrument est un réseau de diffraction fonctionnant en réflexion, constitué de éléments répartis uniformément sur une longueur , comme indiqué sur la Fig. 5. On peut se les représenter comme des bandes réfléchissantes de largeur , et on note le pas du réseau, avec . Il est éclairé sous une incidence par une onde lumineuse plane, et on considère les rayons réfléchis avec un angle . On commence par supposer que chaque élément du réseau est infiniment étroit ( ), et que l'onde plane incidente est monochromatique, de pulsation . Le champ électrique qui la caractérise peut alors être représenté en notation complexe par
On notera la convention utilisée ici pour la phase de l'onde, à savoir et non . On notera aussi que cette écriture (21) nous place dans l'approximation scalaire et on ignore donc tout effet lié à la polarisation. Le vecteur d'onde incident est , avec le nombre d'onde. Les différents éléments du réseau sont repérés par les vecteurs avec un entier variant de 0 à .
Q36. Montrer que le champ électrique incident sur l'élément s'écrit
en exprimant le déphasage en fonction de et .
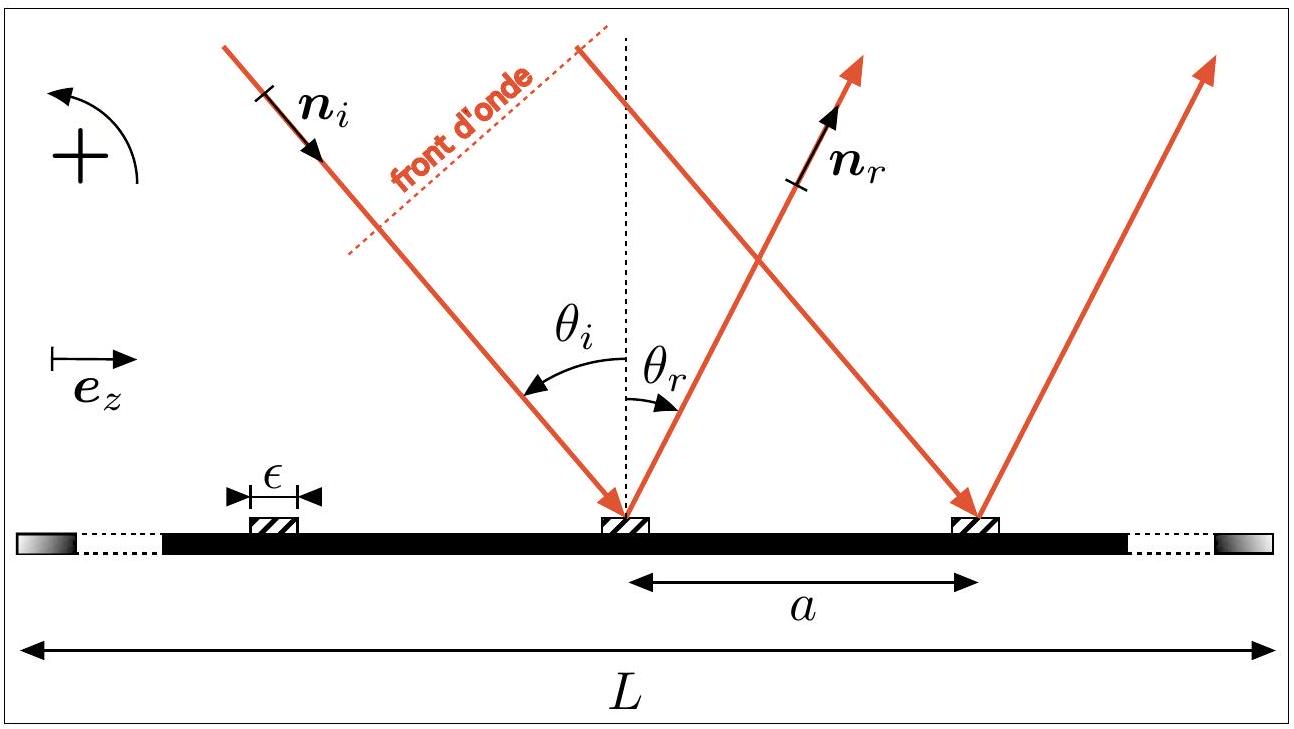
Figure 5 - Schéma d'un réseau en réflexion de pas . Les angles sont comptés algébriquement selon la convention indiquée. On a donc, dans le cas représenté ici, et .
Q37. Chaque élément est la source d'une onde plane dans la direction , dont le champ électrique est
où le coefficient de réflexion complexe est supposé de module unité, . Le vecteur d'onde réfléchi est , ce qui suppose que la réflexion se fait sans changement de la longueur d'onde. Montrer que cette onde peut se mettre sous la forme
en précisant l'expression du déphasage en fonction de et . Pour la suite on posera .
Q38. En déduire que l'onde réfléchie totale dans la direction est aussi une onde plane progressive monochromatique, dont le champ électrique est représenté par
en explicitant l'amplitude complexe en fonction de et .
Q39. Montrer que l'interférence des ondes réfléchies par deux éléments adjacents et est constructive si et seulement si et vérifient la relation
où est un entier relatif quelconque appelé ordre de diffraction. Cette relation constitue la formule des réseaux en réflexion. Dans ce cas, les interférences entre les ondes réfléchies sont bien évidemment toutes constructives.
Q40. Montrer que l'intensité lumineuse dans la direction peut se mettre sous la forme
où est une constante qu'on ne cherchera pas à calculer.
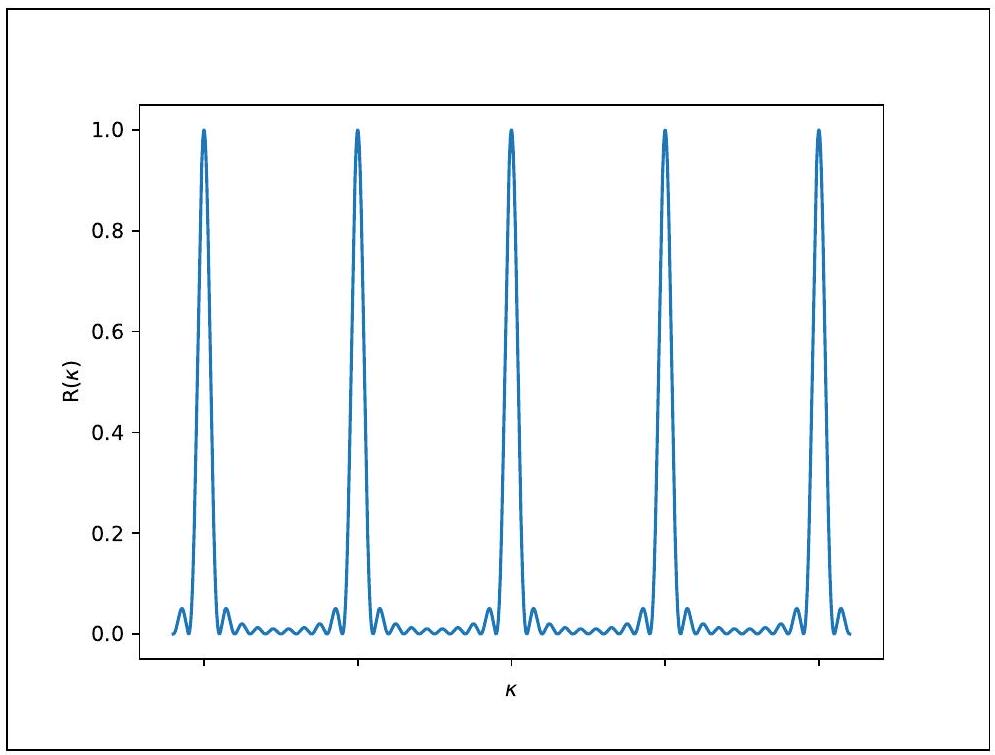
Figure 6 - Fonction réseau .
Q41. La fonction réseau est représentée sur la Fig. 6 mais sans l'indication des valeurs des abscisses. Que valent l'écart entre deux pics consécutifs (où ) et la largeur caractéristique de chacun de ces pics (calculée comme étant l'intervalle entre les premières annulations de part et d'autre du pic)? On exprimera ces grandeurs en fonction de et .
Q42. On considère une lumière dont le spectre couvre l'intervalle , où les deux longueurs d'onde extrêmes correspondent au bleu et au rouge. Par exemple, la couverture spectrale de HARPS va de à . On suppose pour simplifier, dans toute la suite, que ce spectre est plat, c'est-à-dire que l'intensité est indépendante de . La lumière est-elle dispersée dans l'ordre ?
Q43. On pose où est l'angle de réflexion de la composante de longueur d'onde dans l'ordre . Représenter graphiquement pour quelques ordres successifs ( ) et en déduire qu'on a un recouvrement des ordres et (en expliquant ce que cela signifie) si
On pourra faire un schéma. À partir de quel ordre observe-t-on un recouvrement dans le cas de HARPS?
Q44. En considérant que deux longueurs d'ondes proches et (avec ) sont distinguables dans l'ordre dès lors que le pic de diffraction de l'une correspond au premier zéro de l'autre, montrer que le pouvoir de résolution du réseau dans l'ordre est . Comment doit-on alors choisir l'ordre dans lequel travailler?
Q45. On tient maintenant compte de la largeur finie de chacun des éléments. Justifier par analogie que le champ électrique associé à l'onde réfléchie par l'élément s'écrit maintenant sous la forme
Q46. En déduire que l'intensité lumineuse dans la direction est alors donnée par
La fonction correspond à la figure de diffraction d'un élément unique. Représenter la nouvelle distribution de l'intensité lumineuse en fonction de , en supposant, pour cet exemple, que . Pour quel ordre de diffraction a-t-on une intensité maximale? Quelle relation classique de l'optique géométrique retrouve-t-on alors?
Q47. À quelle difficulté se heurte-t-on pour travailler à fort pouvoir de résolution?

II. 6 - Un réseau échelle "blazé"

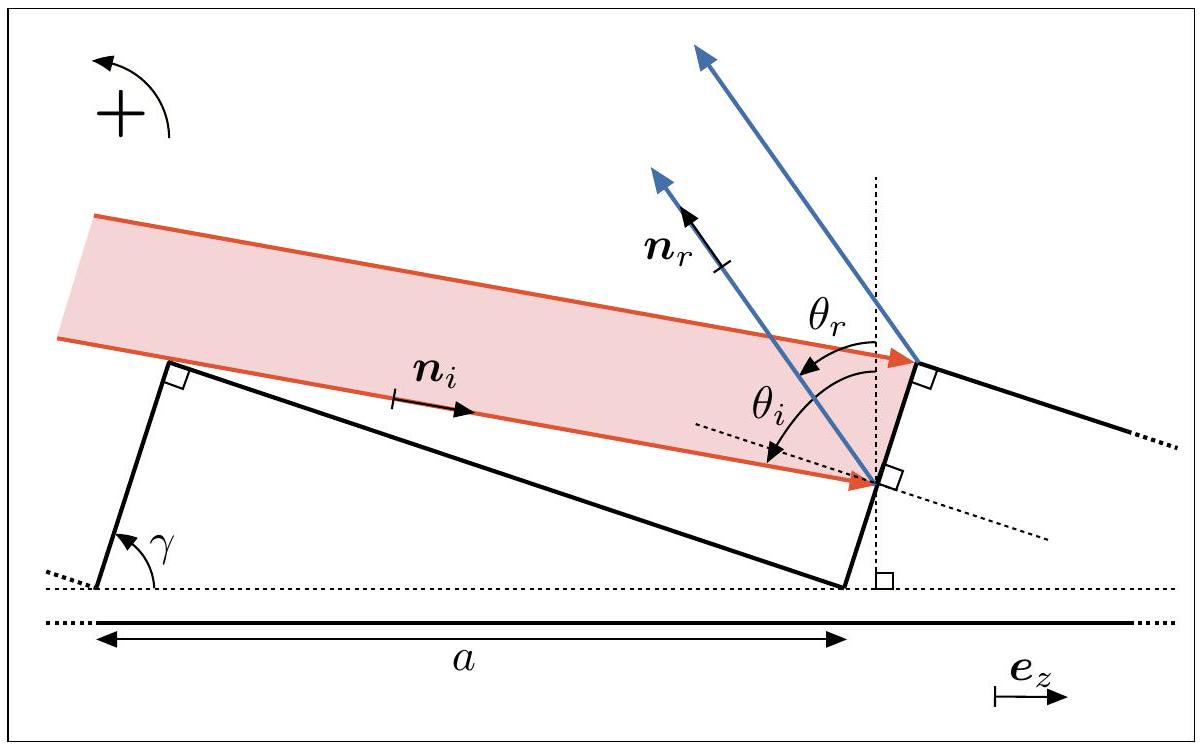
Pour remédier à ce problème, les réseaux sont en pratique blazés pour présenter un maximum de luminosité dans un ordre . Pour ces réseaux, la forme du motif est celle représentée sur la Fig. 7. On appelle l'angle de blaze. On ne cherchera pas à calculer la forme de la nouvelle figure de diffraction associée à ce motif individuel, et on admettra que son maximum correspond à la direction déterminée par la relation de l'optique géométrique retrouvée à la question Q46. On suppose également que l'angle d'incidence est grand, avec .
Figure 7 - Schéma d'un motif de réseau en réflexion blazé.
Q48. Déterminer l'angle correspondant au maximum de luminosité de , en fonction de et .
Q49. Le réseau échelle de HARPS fonctionne dans la configuration de Littrow, pour laquelle l'incidence est normale sur les facettes courtes du motif du réseau. Que devient alors ? En déduire l'expression de l'ordre de diffraction dans lequel se concentre le maximum d'émission, en fonction de et . Inverser cette relation pour obtenir , longueur d'onde de la composante la plus intense dans un ordre donné.
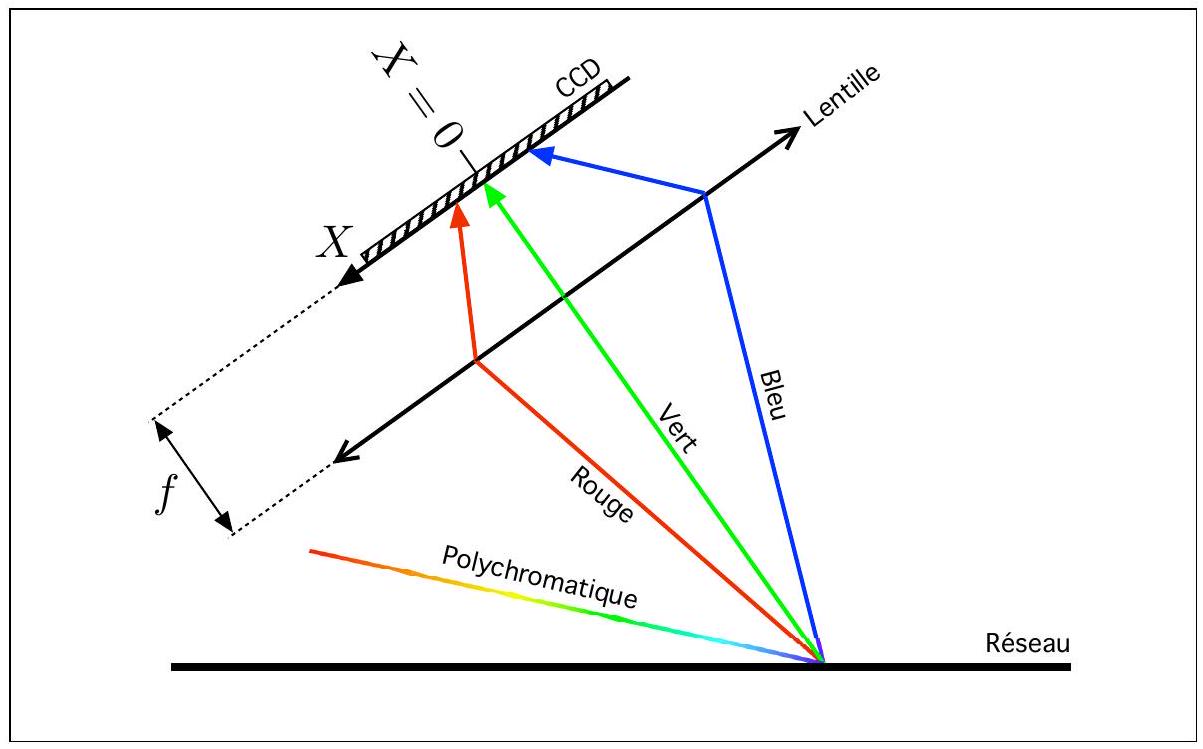
Q50. HARPS présente un angle de blaze , et contient 31,6 éléments individuels par millimètre. En déduire une estimation (grossière) des ordres et dans lesquels les longueurs d'ondes extrêmes présentent le maximum de luminosité.
Figure 8 - Montage Réseau-Lentille-CCD
Q51. En sortie du réseau, on place une lentille, de focale , comme indiqué sur la Fig. 8, et une barrette CCD qui sert de détecteur dans le plan focal de cette lentille. On précise qu'une barrette CCD est un ensemble de détecteurs ponctuels placés les uns à côté des autres sur une ligne, et repérés par une coordonnée . On place cette barrette de telle sorte que corresponde à . On pose et on suppose que . Quelle est la relation entre et ?
Q52. Montrer que pour un ordre de diffraction donné, la position de la radiation de longueur d'onde sur le détecteur est donnée par
Représenter graphiquement en fonction de , pour quelques ordres .
À une position donnée sur le détecteur, ou - ce qui revient au même - dans une direction donnée, on a donc une superposition d'un ensemble discret de composantes de longueurs d'onde , solutions de l'équation . Pour les séparer, on dispose un second élément disperseur entre le réseau échelle et le détecteur. Ce second élément est typiquement un grism, c'est-à-dire un prisme auquel on accole un réseau de diffraction en transmission. Pour parvenir à séparer les ordres qui se recouvrent, on place ce grism de telle sorte qu'il disperse la lumière perpendiculairement à la direction . C'est ce qu'on appelle une dispersion croisée. On ne la traitera pas ici.

III. Détection par la méthode des transits

La méthode la plus efficace en termes de nombres de détections est désormais la méthode des transits. Elle repose sur l'observation de très faibles fluctuations de luminosité d'une étoile dues au passage d'une planète s'interposant entre elle et l'observateur, de manière tout à fait comparable à ce qui se passe sur Terre pendant une éclipse du Soleil par la Lune. Cette configuration est appelée transit. 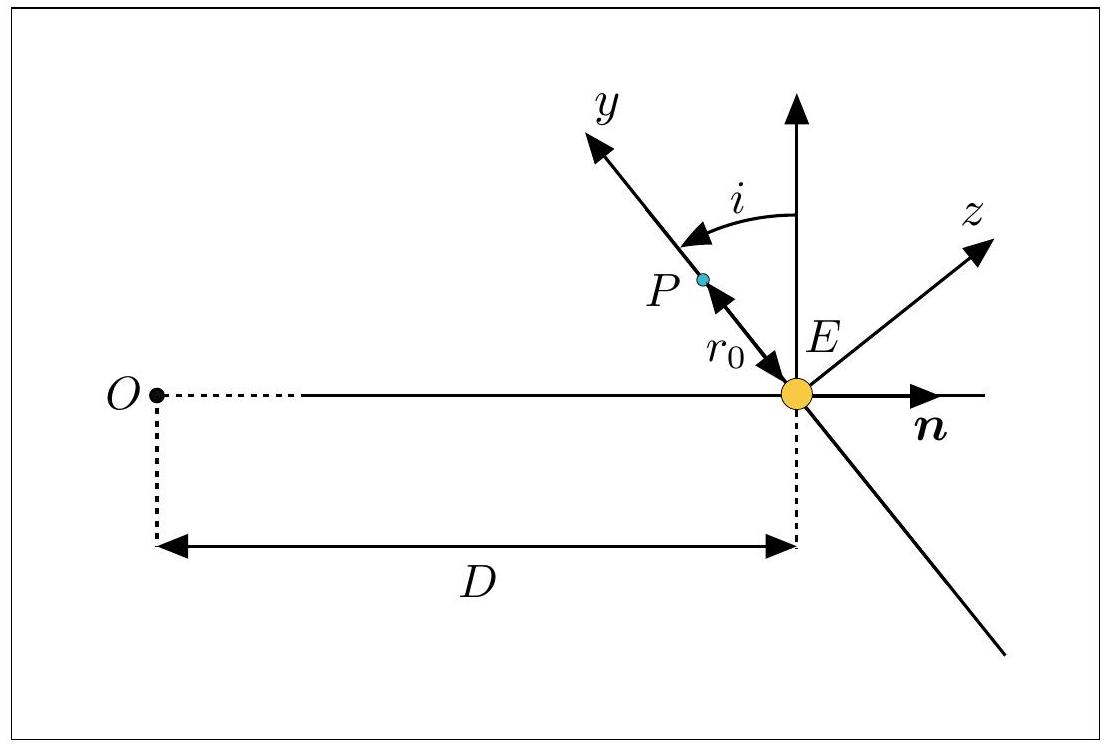On considère donc dans cette partie un système constitué d'une étoile de masse , assimilée à une sphère de rayon et émettant un rayonnement de corps noir à la température , et d'une planète de masse et de rayon . On suppose pour l'instant, et ce jusqu'à la question Q64 incluse, que cette planète n'émet pas par elle-même. L'orbite de la planète autour de l'étoile est supposée circulaire de rayon , et inclinée d'un angle par rapport au plan du ciel. On suppose que le rapport des masses est suffisamment petit pour qu'on puisse considérer que le centre de masse du système est confondu avec le centre de l'étoile, de sorte qu'on a la configuration présentée sur la Fig. 9 ci-dessous.
Figure 9 - Configuration de l'orbite planétaire discutée dans cette partie.

III. 1 - Caractéristiques d'un transit sur la courbe de lumière

Q53. Exprimer l'angle apparent maximal entre la planète et l'étoile, vu depuis la Terre, laquelle est située à une distance . Quelle approximation est-il probablement légitime de faire sur les paramètres qui interviennent dans cette expression? On admettra dans toute la suite que cet angle est suffisamment petit pour que le système planétaire ne soit pas résolu spatialement par le télescope. La seule mesure accessible sur Terre est alors la puissance lumineuse émise par le système entier {étoile+planète}.
Q54. Établir la condition sur l'angle pour qu'un transit puisse être observé. On se placera d'abord dans un cas général, puis on simplifiera la condition obtenue dans le cas où le rayon de la planète est très petit devant celui de l'étoile, .
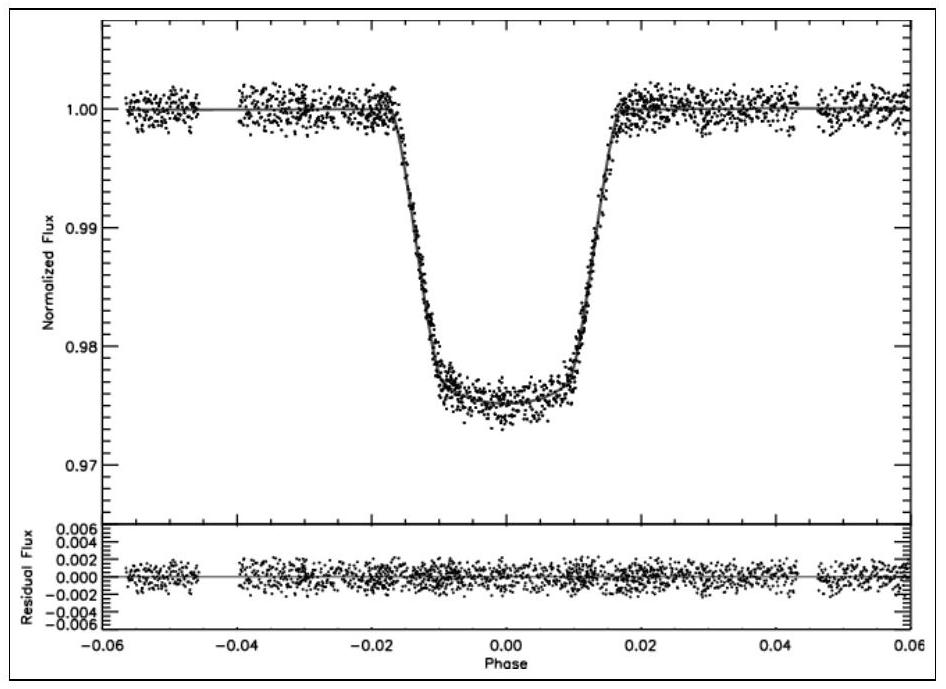
Q55. Si l'on considère un ensemble de tels systèmes planétaires, tous identiques à l'exception de l'angle d'inclinaison de l'orbite , qu'on suppose être aléatoire et distribué uniformément entre et , quelle est la probabilité d'observer un transit exoplanétaire en observant un de ces systèmes au hasard?
Figure 10 - Puissance lumineuse spectrale normalisée reçue de l'étoile HD198733 (Sing et al., 2009).
La Fig. 10 représente la puissance lumineuse spectrale (voir ) reçue en direction de l'étoile HD189733, autour de . Elle est normalisée à celle reçue lorsque la planète n'occulte pas l'étoile. Les données, issues du Hubble Space Telescope, sont représentées par les points, et la courbe en trait plein montre un ajustement de ces données. La figure du bas représente les résidus, une fois la courbe d'ajustement soustraite des données. L'axe des abscisses représente la phase orbitale, qui va normalement de à pour une orbite complète, mais sur cette figure elle a été renormalisée d'une manière qui n'est pas précisée dans l'article d'origine, ce qui la rend inexploitable en l'état.
Q56. Identifier quatre instants particuliers sur cette courbe et représenter sur un schéma montrant le disque stellaire et le disque planétaire les quatre configurations correspondantes, qu'on nomme premier, deuxième, troisième et quatrième contact.
Q57. Montrer que la puissance spectrale peut se mettre sous une forme faisant intervenir la surface apparente du disque stellaire . On notera la surface du détecteur utilisé. En déduire de manière géométrique l'expression de la puissance spectrale reçue lorsque la planète est au milieu de son transit devant l'étoile.
Q58. Montrer que l'on peut déduire le rayon de l'exoplanète à partir de la mesure de la profondeur du transit, si l'on connaît le rayon de l'étoile. Quelle serait la chute relative de puissance spectrale mesurée par une civilisation extraterrestre observant le transit de Jupiter devant le Soleil? Celui de la Terre? Estimer le rayon de la planète HD189733b, sachant que le rayon de l'étoile est .
Q59. Pour un angle , à quelle condition peut-on supposer que la trajectoire de la planète passant devant son étoile, projetée sur le plan du ciel, est une droite? On se placera dans ce cas pour la suite.
Q60. Lors du transit de la planète, la distance apparente - c'est-à-dire projetée sur le plan du ciel - entre le centre de l'étoile et le centre de la planète varie au cours du temps. On appelle paramètre d'impact et on note sa plus petite valeur. On suppose que . Montrer que le temps entre le premier et le quatrième contact vaut
et que celui entre le deuxième et le troisième contact vaut quant à lui
où est la période orbitale de la planète. On justifiera soigneusement le raisonnement.
Q61. En déduire l'expression du paramètre d'impact en fonction de et de ces deux durées. Simplifier cette expression dans le cas . Estimer pour le cas de HD189733b.
Q62. Sachant que la période orbitale de HD189733b est jours et que la durée du transit total est d'environ 6000 s (Beaulieu et al., 2009), en tirer une estimation grossière du rayon .
Q63. Quelle est la relation entre le paramètre d'impact et l'angle d'inclinaison ? En déduire une estimation de dans le cas de HD189733b. On pourra donner une valeur en radians.
Q64. Comment pourrait-on obtenir une estimation de la masse de l'étoile HD189733 à l'aide des résultats précédents? En donner une estimation grossière.

III. 2 - Détection de l'antitransit

Jusqu'à présent, nous avons ignoré le fait que la planète est susceptible d'émettre par elle-même, notamment dans le domaine infrarouge. Ceci est lié au fait que la planète est chauffée par le rayonnement reçu de la part de son étoile, et qu'à l'équilibre thermique, la puissance absorbée doit être contrebalancée par une puissance émise. On admet que la planète est ainsi portée à une certaine température uniformément sur toute sa surface, et on fait l'hypothèse que, comme l'étoile, elle se comporte comme un corps noir. Cette modélisation va nous permettre d'interpréter la Fig. 11, qui représente la courbe de lumière observée par la mission spatiale Kepler en direction de l'étoile HAT-P7, sur plus d'une période orbitale. Les données brutes sont représentées par les points noirs fins, les points verts plus épais sont des moyennes lissées permettant de réduire le bruit, et la courbe en trait plein est un ajustement sur ces moyennes. La figure du bas montre la même courbe mais avec une échelle en ordonnées fortement agrandie.
Q65. Comment interpréter la faible chute de la courbe de lumière entre deux transits? On appelle antitransit cette configuration du système {étoile+planète}. On appellera disjonction les configurations intermédiaires entre le transit et l'antitransit.
Q66. Sachant que , que peut-on dire de la relation entre les intensités spécifiques issues de l'étoile et de la planète ?
Q67. On note , et les puissances spectrales lumineuses reçues par l'observateur, dans les trois configurations décrites (transit, antitransit, disjonction). En posant , exprimer ces puissances spectrales en fonction de et .
Q68. Représenter schématiquement une courbe de lumière complète théorique à partir des expressions trouvées ci-dessus pour , et .
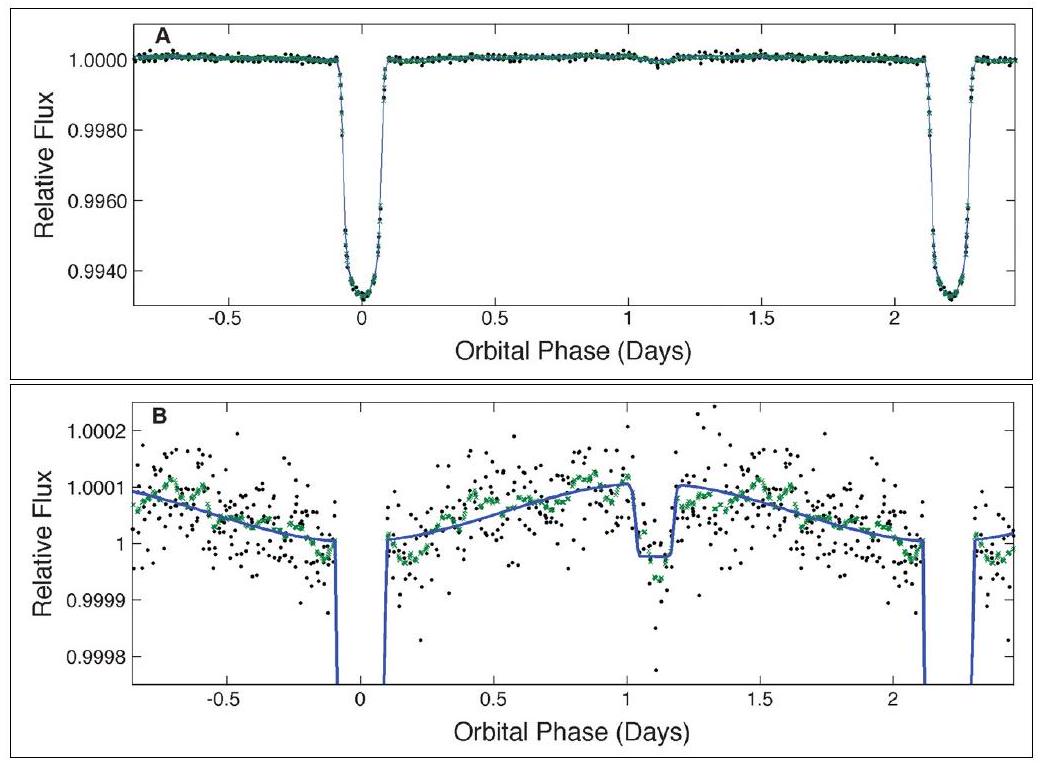
Figure 11 - Puissance lumineuse normalisée reçue de l'étoile HAT-P7 (Borucki et al., 2009). Les données brutes sont représentées par les points noirs fins, les points verts plus épais sont des moyennes lissées permettant de réduire le bruit, et la courbe en trait plein est un ajustement sur ces moyennes. La figure du bas montre la même courbe que celle du haut, mais avec une échelle en ordonnées fortement agrandie.
Q69. Quelle différence constate-t-on entre ce modèle et l'observation de la Fig. 11? Quel phénomène a-t-on omis qui pourrait expliquer cette différence? On justifiera la réponse.
Q70. Dans le cas d'une orbite elliptique, montrer que l'on peut en principe déduire de la courbe de lumière une estimation de l'excentricité de l'orbite. On pourra se placer dans le cas d'une orbite dont le grand axe est perpendiculaire à la ligne de visée, et on ne cherchera pas à calculer explicitement . L'orbite de HAT-P7b est-elle faiblement ou fortement excentrique?
Q71. Du fait du bruit inhérent aux mesures, il faut observer un grand nombre d'orbites pour détecter un signal dans la courbe de lumière. Ce signal, , est bien entendu la chute relative de puissance lumineuse reçue, représentée sur la courbe de la Fig. 11. Le bruit , quant à lui, correspond à l'amplitude de la dispersion des mesures autour de cette courbe. Si l'on note le nombre d'orbites nécessaires pour atteindre un rapport signal-à-bruit donné pour la détection du transit de HAT-P7b, quel serait l'ordre de grandeur du nombre d'orbites nécessaires pour détecter l'antitransit avec le même rapport signal-à-bruit? Faire l'application numérique.
    1. http://nameexoworlds.iau.org
    1. Ces deux angles sont associés au système de coordonnées sphériques. On fait remarquer que est le même angle que celui qui nous a servi à la question Q4 .
ENS Physique C PC 2019 - Version Web LaTeX | WikiPrépa | WikiPrépa