Version interactive avec LaTeX compilé
SESSION 2004
Filière PC
PHYSIQUE
ENS de Paris
Durée : 6 heures
L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est admise sur la table ou le poste de travail, et aucun échange n'est autorisé entre les candidats.
L'objectif de ce problème est de décrire l'interaction rayonnement-interface dans le cas de la déformation d'une interface entre deux fluides par un laser. Le sujet se décompose en trois parties largement indépendantes. On se place à température constante
En coordonnées cylindriques (
En coordonnées cylindriques (
où on note
On donne également les relations:
On donne également les relations:
où le symbole
La formule du double produit vectoriel s'écrit:
La formule du double produit vectoriel s'écrit:
On prendra pour les applications numériques les valeurs suivantes :
Table des valeurs
masse volumique de l'air
masse volumique de l'eau
masse volumique du mélange eau-huile lourd
masse volumique du mélange eau-huile léger
tension superficielle air/eau
tension superficielle (eau-huile lourd) /(eau-huile léger)
indice optique de l'air
indice optique de l'eau
indice optique du mélange eau-huile lourd
indice optique du mélange eau-huile léger
largeur du faisceau laser
gravité
vitesse de la lumière
élément d'aire en coordonnées sphériques:
masse volumique de l'air
masse volumique de l'eau
masse volumique du mélange eau-huile lourd
masse volumique du mélange eau-huile léger
tension superficielle air/eau
tension superficielle (eau-huile lourd) /(eau-huile léger)
indice optique de l'air
indice optique de l'eau
indice optique du mélange eau-huile lourd
indice optique du mélange eau-huile léger
largeur du faisceau laser
gravité
vitesse de la lumière
élément d'aire en coordonnées sphériques:
1 Tension de surface
On considère deux fluides (notés F1 et F2) distincts immiscibles séparés par une interface d'aire
On suppose que lors d'une transformation infinitésimale réversible l'aire de cette surface varie d'une grandeur
où le coefficient
1.1
Donner l'origine physique de ce travail.
1.2
Quelle est la dimension de la tension superficielle
1.3
En considérant la déformation plane d'un rectangle de section
1.4
On suppose que l'interface F1-F2 est une sphère de rayon
a) Calculer la variation d'énergie
b) A l'équilibre, montrer alors qu'il existe un saut de pression entre les deux fluides appelé pression superficielle :
a) Calculer la variation d'énergie
b) A l'équilibre, montrer alors qu'il existe un saut de pression entre les deux fluides appelé pression superficielle :
c) Calculer la surpression à l'intérieur d'une bulle d'air de 1 mm de diamètre, entourée d'eau. En déduire la surpression dans une bulle de savon de même rayon. La comparer à la pression atmosphérique. Cette bulle contient de l'air et est séparée de l'air extérieur par une membrane de rayon
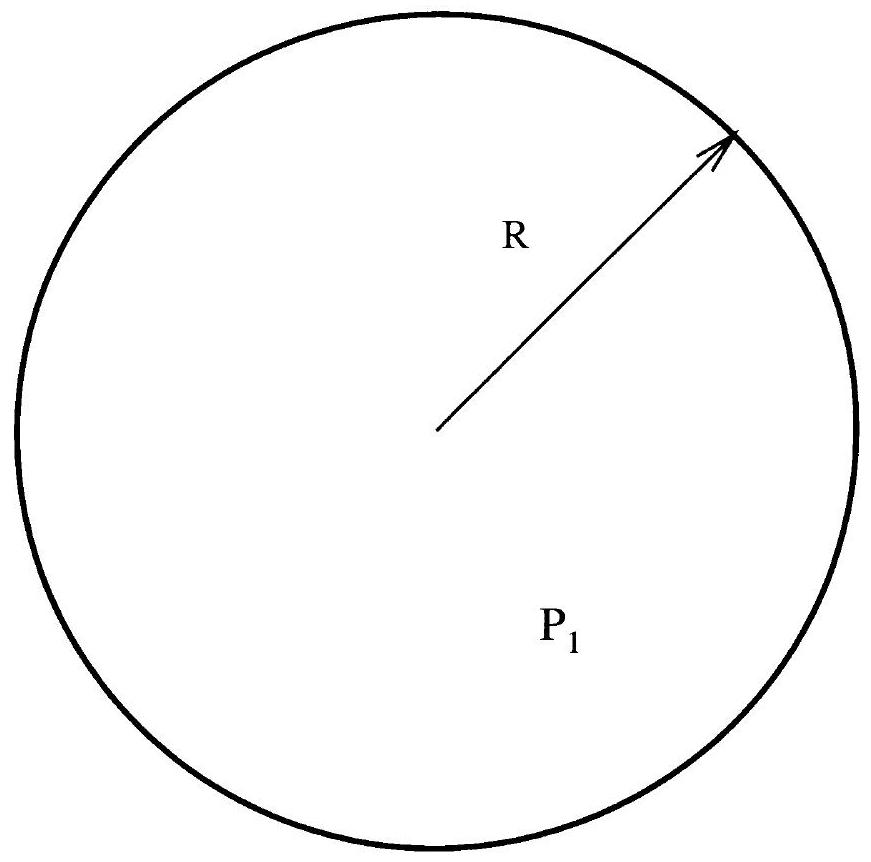
Figure 1: Bulle de rayon R du fluide F 1 (pression
d) Sous quelle condition a-t-on pu négliger la gravité? Pour déterminer cette condition on calculera la variation de pression due à la gravité et liée à la différence de masse volumique entre le fluide F1 et le fluide F2. Pour une bulle d'air dans l'eau, calculer le rayon typique au dessous duquel on peut négliger la gravité.
e) On considère la même situation avec des fluides F1 et F2 très similaires, composés chacun d'un mélange eau-huile de différentes concentrations relatives. Le fluide F 1 , le plus lourd a pour masse volumique
d) Sous quelle condition a-t-on pu négliger la gravité? Pour déterminer cette condition on calculera la variation de pression due à la gravité et liée à la différence de masse volumique entre le fluide F1 et le fluide F2. Pour une bulle d'air dans l'eau, calculer le rayon typique au dessous duquel on peut négliger la gravité.
e) On considère la même situation avec des fluides F1 et F2 très similaires, composés chacun d'un mélange eau-huile de différentes concentrations relatives. Le fluide F 1 , le plus lourd a pour masse volumique
1.5
Retrouver la formule (1) en considérant le bilan des forces s'exerçant sur une calotte sphérique de l'interface (voir figure 2).
1.6
a) Que devient le calcul précédent pour une interface à symétrie de révolution, donnée par
b) Dans la limite des faibles variations de
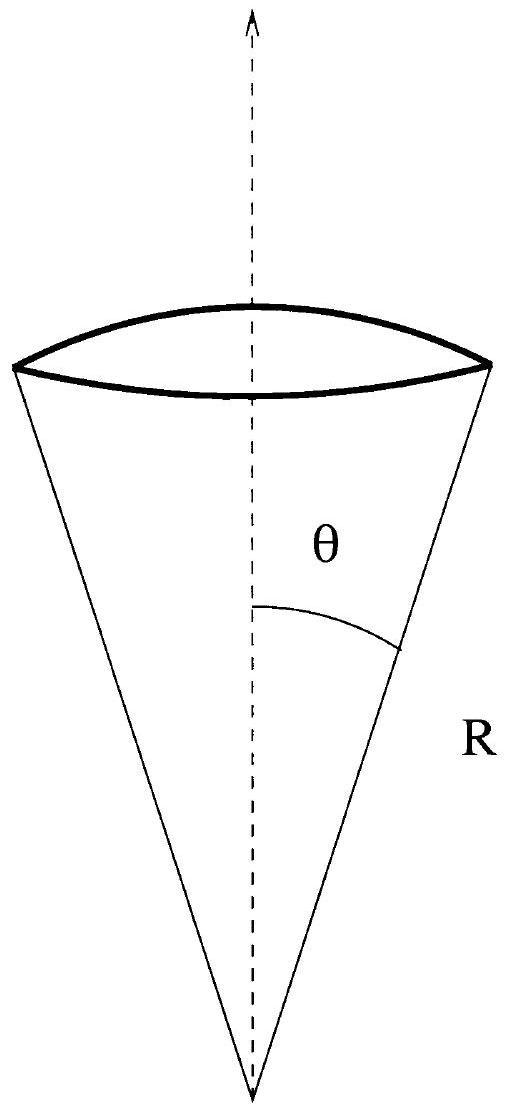
Figure 2: Schéma de la calotte de demi-angle au sommet
2 Ondes électromagnétiques et interface
On considère un milieu diélectrique quelconque sans effets magnétiques. On appelle
On note les équations de Maxwell dans ce milieu:
où on a introduit
2.1
a) Soit
b) On suppose le milieu non absorbant. Rappeler la propriété que doit satisfaire
ce cas.
c) Montrer que les champs
b) On suppose le milieu non absorbant. Rappeler la propriété que doit satisfaire
ce cas.
c) Montrer que les champs
2.2
On cherche les solutions des équations de Maxwell sous la forme
a) Donner la relation de dispersion reliant
b) Quelle est la vitesse de la lumière dans le milieu? En déduire la valeur de l'indice optique
c) Relier
a) Donner la relation de dispersion reliant
b) Quelle est la vitesse de la lumière dans le milieu? En déduire la valeur de l'indice optique
c) Relier
2.3
Le vecteur de Poynting
a) Donner la valeur instantanée du vecteur de Poynting
b) Calculer sa valeur moyenne temporelle
c) On définit l'intensité
d) A partir des équations de Maxwell, retrouver la densité instantanée d'énergie électromagnétique
b) Calculer sa valeur moyenne temporelle
c) On définit l'intensité
d) A partir des équations de Maxwell, retrouver la densité instantanée d'énergie électromagnétique
2.4
Les fluides F1 et F2 considérés dans la première partie sont en fait deux milieux diélectriques d'indices optiques
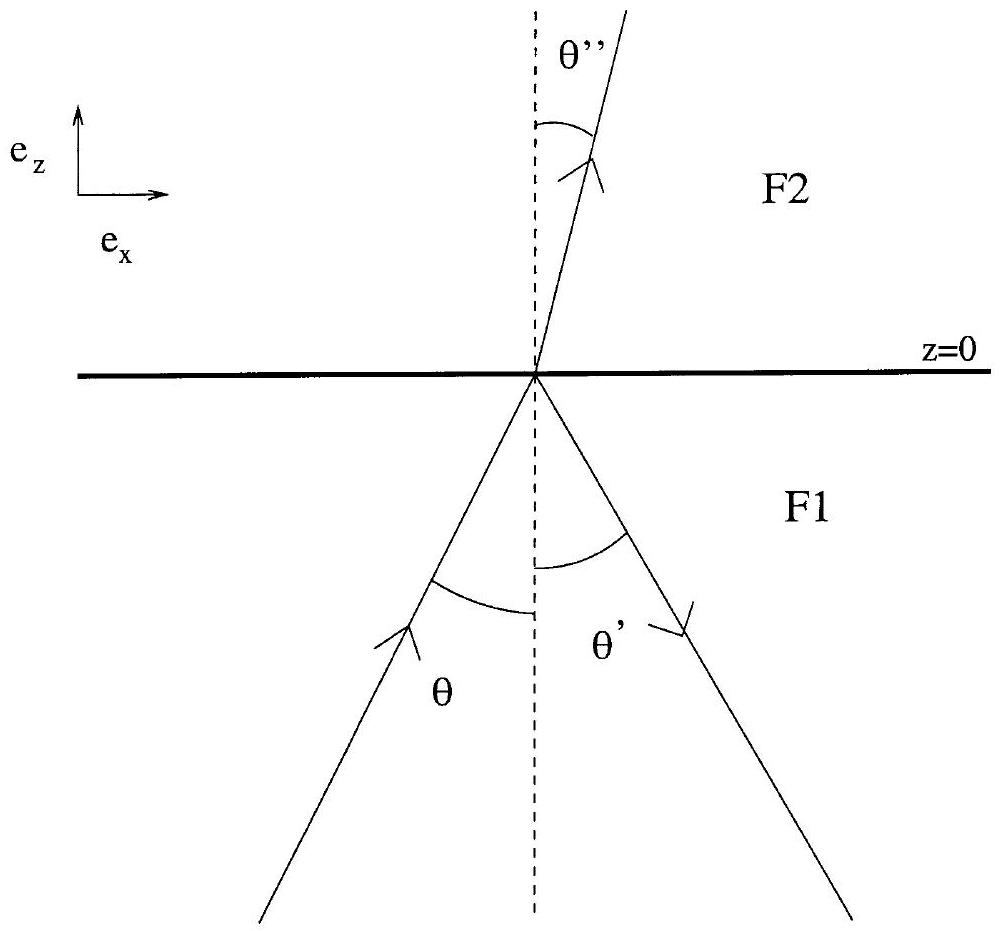
Figure 3: Schéma de la propagation d'une onde électromagnétique à l'interface F1-F2.
une onde transmise (
a) Exprimer
b) On note
a) Exprimer
b) On note
2.5
a) A partir des équations de Maxwell, écrire les conditions aux limites sur les champs à l'interface 1-2.
b) Exprimer
c) On suppose les vecteurs complexes
d) A partir de 2.5 a ), relier
e) On définit les coefficients de réflexion et de transmission
b) Exprimer
c) On suppose les vecteurs complexes
d) A partir de 2.5 a ), relier
e) On définit les coefficients de réflexion et de transmission
2.6
a) Calculer le vecteur de Poynting et la densité d'énergie électromagnétique en moyennes temporelles pour chaque onde (incidente, réfléchie, transmise). Exprimer ces quantités en fonction de
b) On admettra qu'à chaque onde électromagnétique est associée une densité de flux de quantité de mouvement
b) On admettra qu'à chaque onde électromagnétique est associée une densité de flux de quantité de mouvement
Le produit du flux de ce vecteur à travers une surface
c) On se place en incidence normale
c) On se place en incidence normale
où
d) Que devient ce saut de pression si on considère que l'onde électromagnétique se propage du milieu 2 vers le milieu 1? Comparer son signe à celui de la situation précédente.
e) Indiquer comment varie la pression de radiation calculée au c) pour de faibles valeurs de
d) Que devient ce saut de pression si on considère que l'onde électromagnétique se propage du milieu 2 vers le milieu 1? Comparer son signe à celui de la situation précédente.
e) Indiquer comment varie la pression de radiation calculée au c) pour de faibles valeurs de
3 Déformation d'une interface par un laser
On se place en coordonnées cylindriques (
allons déterminer dans cette partie la relation que satisfait cette solution statique
allons déterminer dans cette partie la relation que satisfait cette solution statique
où
3.1 Condition d'équilibre
a) Calculer la pression
b) Calculer de même la pression
c) En déduire la relation à l'équilibre pour de faibles variations de
b) Calculer de même la pression
c) En déduire la relation à l'équilibre pour de faibles variations de
3.2 Longueurs caractéristiques
On notera
a) Comparer les deux termes du membre de gauche de l'équation (4). En déduire la longueur typique
b) Quelle est la longueur typique de variation de
c) Calculer
a) Comparer les deux termes du membre de gauche de l'équation (4). En déduire la longueur typique
b) Quelle est la longueur typique de variation de
c) Calculer
3.3 Equilibre gravité/laser
a) Donner la forme de l'interface
b) On notera
c) Tracer l'allure de l'interface
b) On notera
c) Tracer l'allure de l'interface
3.4 Solution générale
Pour déterminer la solution de (4), on considère la transformée de Fourier-Bessel
où la fonction
avec
a) Montrer alors que la fonction
est solution de (4).
b) Exprimer
b) Exprimer
c) On admet que pour
3.5 Déformation non linéaire
Lorsque l'interface se déforme trop, on ne peut plus considérer que l'onde arrive en incidence normale sur la partie déformée de l'interface.
a) En fonction de
b) Déterminer l'équation que satisfait alors
c) Lorsque l'intensité de l'onde augmente, on observe des déformations importantes de l'interface. En particulier, on remarque pour
a) En fonction de
b) Déterminer l'équation que satisfait alors
c) Lorsque l'intensité de l'onde augmente, on observe des déformations importantes de l'interface. En particulier, on remarque pour
est satisfaite pour au moins une valeur de
d) Calculer la puissance
d) Calculer la puissance
