L'usage de calculatrices électroniques de poche sans document d'accompagnement est autorisé, y compris les calculatrices programmables et alphanumériques ou à écran graphique, à condition que leur fonctionnement soit autonome et qu'il ne soit pas fait usage d'imprimante. Une seule calculatrice à la fois est admise sur la table et aucun échange n'est autorisé entre les candidats.

Quelques questions de sismologie

Cette épreuve comporte quatre problèmes indépendants.

A. Rais sismiques

Les rayons (ou rais) sismiques obéissent aux mêmes lois que les rayons lumineux en optique géométrique, l'indice de réfraction

étant remplacé par

l'inverse de la vitesse des ondes sismiques. Considérons un modèle simple de terrain, constitué de couches homogènes infiniment fines, horizontales, de vitesse

à la profondeur

(figure 1). En un point d'un rai, on note

l'angle entre le rai et la verticale. On considère que l'émission de l'onde sismique a lieu en surface (point O ) et on note

la valeur de

en ce point pour un rai donné ainsi que

la valeur de la vitesse en surface.

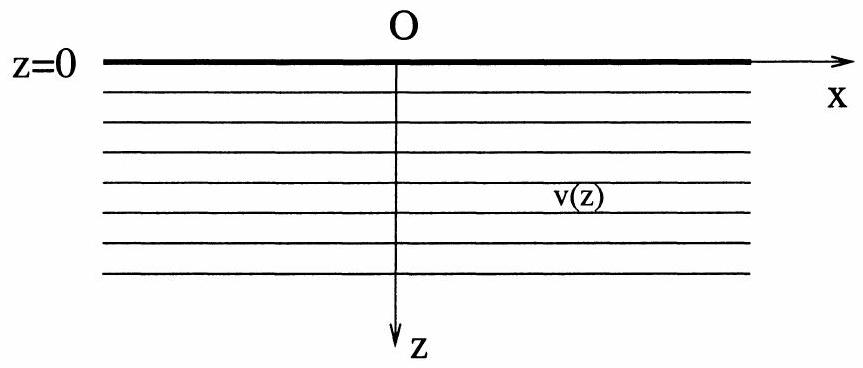
Fig. 1 - Terrain à symétrie plane.

Donner et expliquer la relation qui lie et .
On donne un modèle de vitesse en figure 2. Quelle est la forme des rais dans la partie I du terrain?
Dans les parties II, III et IV, les rais sont-ils recourbés vers le haut ou vers le bas?
On appelle point bas d'un rai, le point où le rai est horizontal. Pourquoi les rais possèdent-t-ils une symétrie par rapport à un axe vertical?
Quelle est la profondeur du point bas du rai tel que ? Dessiner qualitativement ce rai.
Même question avec . Dessiner ce rai sur le même schéma que précédemment.
Même question avec .
Peut-il y avoir des points bas dans la partie III?
Vers , il y a un phénomène qu'on appelle zone d'ombre. Expliquer. Comment peut-on déterminer la valeur de cet angle à partir des données du problème?
En approximant le rai par quelques morceaux de droites, estimer la distance de retour en surface du rai tel que .

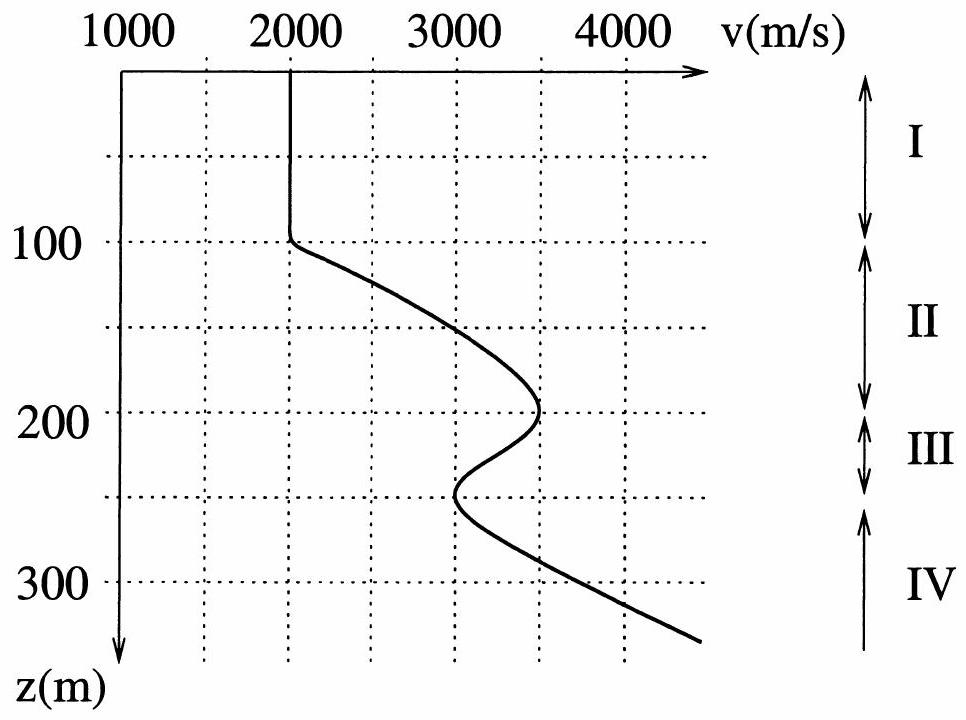
Fig. 2 - Vitesse

en fonction de la profondeur

B. Sismomètre simplifié

Afin d'analyser la réponse d'un sismomètre aux mouvements du sol, schématisons un sismomètre vertical par une masse

suspendue à une potence par l'intermédiaire d'un ressort de raideur

(figure 3).

Quel est l'allongement du ressort quand on lui adjoint la masse?
Soit le déplacement du sol dans un référentiel galiléen. Écrire l'équation différentielle du mouvement reliant à l'allongement du ressort.
Soit un mouvement du sol sinusoïdal . Montrer que est solution et représenter la valeur absolue de en fonction de . Commenter la courbe obtenue.
Montrer qu'à haute fréquence, le sismomètre enregistre le déplacement du sol et qu'à basse fréquence, il enregistre son accélération. Avec
, que peut-on choisir comme valeur(s) de la masse si on veut enregistrer le déplacement du sol à des périodes de l'ordre de une seconde?

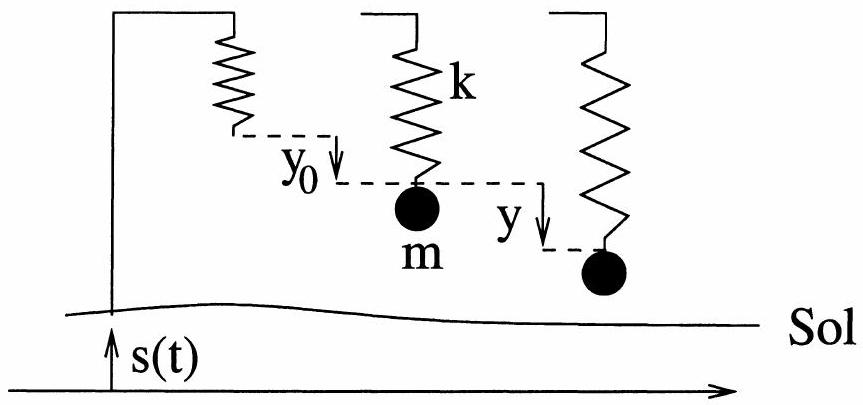
Fig. 3 - Sismomètre simplifié sans la masse (gauche), avec la masse, au repos (milieu), en mouvement (droite).

C. Mode de translation de la graine

Nous allons traiter du mouvement en translation de la graine (ou noyau interne de la Terre) supposée rigide au sein du noyau (externe) fluide. Cette oscillation en régime libre est connue sous le nom de mode de Slichter. On approximera la graine par une particule de faible taille et on admettra que son déplacement s'effectue sur une droite passant par le centre de la Terre.

Soit donc une petite particule sphérique solide de rayon

et de masse volumique

située au voisinage du centre de la Terre, dans le noyau fluide homogène de masse volumique

. La particule et le noyau sont supposés être incompressibles. On note

la gravité au rayon

la constante de gravitation universelle.

Au voisinage du centre, la gravité est de la forme où est une constante. Voyez-vous une raison pour que soit de cette forme?
La gravité vérifie l'équation . Exprimer en fonction des autres données du problème.
Le noyau est supposé être un fluide parfait. La particule se trouve maintenant à un petit rayon . Faire le bilan des forces sur la particule. L'équilibre au centre est-il stable ou instable?
Donner l'équation différentielle vérifiée par .
Résoudre cette équation et décrire le mouvement. On donnera les quantités caractéristiques du mouvement ainsi que des analogues physiques.
On assimile la graine de la Terre à cette particule. On donne alors . Donner les valeurs numériques des quantités caractéristiques du mouvement.
Des théoriciens de la physique des liquides estiment que la viscosité dynamique du noyau est de l'ordre de s. On suppose maintenant que le noyau est un fluide visqueux et que l'on peut appliquer la loi de Stokes. Donner la nouvelle équation différentielle vérifiée par , la résoudre et dessiner l'allure de la fonction . De quel type de mouvement s'agit-il?
Les estimations de certains sismologues conduisent à des valeurs de s. Calculer les temps caractéristiques d'atténuation du mouvement pour les deux valeurs de la viscosité.
En considérant un déplacement de la graine de l'ordre du millimètre, discuter la validité de l'application de la loi de Stokes.
Représenter qualitativement les portraits de phase des mouvements sans viscosité et avec viscosité.
Décrire les types d'énergies en jeu dans ces mouvements, ainsi que leur variation au cours du temps.
N.B. : Le mode de Slichter n'a, à l'heure actuelle, pas été détecté de façon indiscutable par l'intermédiaire des sismomètres ou des gravimètres.

D. Ondes sismiques et diffusion thermique

Nous cherchons dans ce problème à quantifier l'influence de la diffusion thermique sur les ondes sismiques. Le milieu est supposé être un liquide parfait compressible et conducteur de chaleur. Les variables dépendent du temps

et d'une seule coordonnée cartésienne

. Les coefficients suivants sont supposés indépendants du temps et de la position : les incompressibilités isentropique et isotherme

, les capacités thermiques isochore et isobare

, la dilatation isobare

, la conductivité thermique

On s'intéresse à un volume parallélipédique

compris à un instant

entre les abscisses

. On note

la section de ce volume perpendiculairement à la direction

, ainsi que

, sa pression, son entropie, son volume, sa température et sa masse volumique.

Certaines parties du problème peuvent être traitées indépendamment des autres.

Échanges de chaleur

Le milieu à l'équilibre est traversé par une onde sismique, c'est-à-dire une perturbation de pression.

Cette onde induit un flux de chaleur ; pourquoi?
Pourquoi ne peut-on pas a priori considérer l'évolution comme réversible?
Montrer que la quantité de chaleur reçue par le volume pendant le temps est .
Rappeler et expliquer l'expression de en fonction de .
En déduire l'expression de en fonction des variations de température.

Principes mécaniques et thermodynamiques

A un instant

, les quantités thermodynamiques deviennent

, etc.
6. L'onde induit une vitesse du milieu

. En comparant le volume aux instants

, montrer que

; on repérera cette relation par la référence (1).
7. En effectuant un bilan des forces montrer que

; ce sera l'équation (2).
8. Calculer le travail des forces de pression sur le volume pendant le temps

et l'exprimer en fonction de

(on supposera que la pression est continue).
9. Rappeler l'expression de

en fonction des variations de

. A l'aide du premier principe de la thermodynamique en déduire que

.
10. Déduire des relations précédentes l'expression de

en fonction de

et des variations de

; ce sera l'équation (3).

Relations thermodynamiques

Montrer que . On admettra dans la suite qu'on a aussi .
En déduire les expressions de et en fonction de et des coefficients thermodynamiques. Ce seront les équations (4) et (5).
Montrer que . On admettra dans la suite qu'on a aussi .

Ondes planes

On cherche maintenant des solutions aux équations couplées (1) à (5) sous la forme d'ondes planes monochromatiques écrites sous forme complexe :

, et où

sont des constantes représentant les valeurs des paramètres à l'équilibre.

sont des coefficients constants très petits devant

.
14. Pourquoi peut-on, dans les relations (1) à (5), remplacer

, et

, lorsqu'ils ne sont pas dérivés, par

, et

.
15. Écrire un système d'équations reliant les coefficients

entre eux. On assimilera pour cela les dérivées

aux dérivées partielles

. Finalement, par souci de concision dans l'écriture, on enlèvera les indices

.
16. En déduire une relation entre

. En notant

les capacités thermiques massiques et

la diffusivité thermique, montrer qu'on peut mettre cette relation sous la forme

avec

Montrer que dans la limite prend une valeur réelle et que la vitesse de l'onde est .
Donner les valeurs correspondantes dans la limite . On les appellera et .
Commenter les deux résultats précédents.

Application à la Terre

Pour les applications numériques, on prendra les valeurs du manteau terrestre vers 600 km de profondeur :

Estimer numériquement et .
Les fréquences des ondes sismiques sont de l'ordre de 1 Hz . En déduire que, dans le cas du manteau terrestre, et sont très grands devant une quantité que l'on précisera et que .
En effectuant le développement limité correspondant, exprimer en fonction de et . En déduire qu'on peut mettre sous la forme où est la longueur d'onde. Donner en fonction de et .
Quelle est la diminution de l'amplitude de l'onde après que celle-ci a parcouru une longueur d'onde? Cette diminution est-elle sensible dans le cas du manteau terrestre? Conclure sur l'influence de la diffusion thermique sur la propagation des ondes sismiques dans la Terre.