J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Option Informatique MP 2022

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2022
Filière
MP
Matière
Info
Mines MPMines 2022MP InfoInfo 2022
2025_08_29_c2b55766fefad687b448g

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL.
Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).

CONCOURS 2022

ÉPREUVE D'INFORMATIQUE MP

Durée de l'épreuve : heures
L'usage de la calculatrice et de tout dispositif électronique est interdit.
Cette épreuve concerne uniquement les candidats de la filière MP.
Les candidats sont priés de mentionner de façon apparente
sur la première page de la copie :
INFORMATIQUE - MP
L'énoncé de cette épreuve comporte 9 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Les sujets sont la propriété du GIP CCMP. Ils sont publiés sous les termes de la licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 3.0 France. Tout autre usage est soumis à une autorisation préalable du Concours commun Mines Ponts.

Préliminaires

Présentation du sujet

L'épreuve est composée d'un problème unique, comportant 27 questions. Dans ce problème, nous étudions un mécanisme pour lire un mot qui a été brouillé (par exemple corekte) et proposer un mot ciblé comme correction de ce mot (par exemple correct). Ce type de traitement est couramment utilisé dans le contexte de la vérification orthographique, de la reconnaissance vocale, de la lecture optique ou encore de la conception de moteurs de recherche tolérant aux requêtes mal formulées.
Après cette section de préliminaires, le problème est divisé en trois sections. Dans la première section (page 1), nous étudions comment mesurer des erreurs commises à la saisie d'un mot par une méthode de programmation dynamique. Dans la deuxième section (page 4), nous étudions comment stocker un corpus de mots par une méthode arborescente et comment fouiller ce corpus à l'aide d'un automate déjà construit. Dans la troisième section (page 7), nous étudions comment construire un filtre de fouille par une méthode inspirée de la théorie des automates.
Dans tout l'énoncé, un même identificateur écrit dans deux polices de caractère différentes désignera la même entité, mais du point de vue mathématique pour la police en italique (par exemple ou ) et du point de vue informatique pour celle en romain avec espacement fixe (par exemple n ou nprime).

Travail attendu

Pour répondre à une question, il sera permis de réutiliser le résultat d'une question antérieure, même sans avoir réussi à établir ce résultat.
Il faudra coder des fonctions à l'aide du langage de programmation OCaml, en reprenant l'en-tête de fonction fourni par le sujet, sans nécessairement recopier la déclaration des types. Quand l'énoncé demande de coder une fonction, sauf demande explicite de l'énoncé, il n'est pas nécessaire de justifier que celle-ci est correcte ou que des préconditions sont satisfaites.
Le barème tient compte de la clarté des programmes : nous recommandons de choisir des noms de variables intelligibles ou encore de structurer de longs codes par des blocs ou par des fonctions auxiliaires dont on décrit le rôle.

1 Une mesure des erreurs de saisie

1.1 Une fonction mystère

La constante entière max_int désigne le plus grand entier représentable par OCaml. Nous nous donnons la fonction mystere suivante.
let rec mystere z = match z with
(* La fonction mystere calcule ... *)
    | [] -> max_int
    | [a] -> a
    | a::b::y -> mystere ((if a <=b then a else b)::y);;
1 - Donner la signature de la fonction mystere. Justifier brièvement.
2 - Dire si, quelle que soit l'entrée respectant le typage, le calcul de mystere z se termine et le démontrer. Préciser, le cas échéant, le nombre d'appels à la fonction mystere.
3 - Compléter sommairement le commentaire de la ligne 2. Énoncer une propriété qui caractérise exactement la valeur de retour de la fonction mystere. Démontrer cette propriété.
Dans la question suivante, le terme complexité en espace désigne un ordre de grandeur asymptotique de l'espace utilisé en mémoire lors de l'exécution d'un algorithme pour stocker tant l'entrée que des résultats intermédiaires et la valeur de retour.
4 - Quelle est la complexité en espace de l'appel mystere z? Est-elle optimale?

1.2 Distance d'édition de Levenshtein

Nous fixons un alphabet de 27 symboles qui se représentent par le type char. L'ensemble des mots sur l'alphabet se note ; la longueur d'un mot se note . Dans toute cette sous-section, nous fixons deux mots : le mot , dit brouillé, de longueur et le mot , dit ciblé, de longueur .
Définition : Nous appelons distance entre un mot brouillé et un mot ciblé , et nous notons dist , le nombre minimum de symboles qu'il faut supprimer, insérer ou substituer à un autre symbole pour transformer le mot brouillé en le mot ciblé . On remarque que .
Par exemple, la distance entre le mot brouillé corekte et le mot ciblé correct vaut 3 : en effet, on peut insérer un , substituer un au et supprimer le e final pour passer du mot au mot ; par ailleurs, on peut vérifier que cette transformation est impossible en effectuant deux opérations ou moins.
Nous notons préf le préfixe de longueur du mot , c'est-à-dire le mot des premiers symboles de . Pour , il s'agit du mot vide . Pour tous les indices compris entre 0 et et pour compris entre 0 et , nous notons préf , préf la distance entre les préfixes préf et préf .
5 - Pour tous les entiers compris entre 0 et et compris entre 0 et , déterminer les distances et .
6 - Pour tous les entiers compris entre 0 et et compris entre 0 et , exprimer la distance en fonction des distances .
Indication Ocaml : Un élément de type char se déclare entre deux apostrophes : par exemple, on code 'a' pour définir le symbole a. Les mots de se représentent par le type char list. Nous déclarons
type mot = char list;;
Nous rappelons la syntaxe des fonctions suivantes :
  • List.length, de type 'a list -> int : la longueur d'une liste est List.length 1 ;
  • Array.make, de type int -> 'a -> 'a array: un tableau de longueur dont chaque case est initialisée avec la valeur s'obtient par Array.make n v. Dans un tableau, les indices sont numérotés à partir de 0 . On accède au coefficient en position du tableau a par l'expression a.(i), on le modifie par l'instruction a.(i) <- v.
    - Écrire une fonction array_of_mot (w:mot) : char array dont la valeur de retour est un tableau formé des symboles du mot écrits dans le même ordre.
Indication Ocaml : Nous rappelons la syntaxe de la fonction suivante :
  • Array.make_matrix, de type int -> int -> 'a -> 'a array array: une matrice de taille dont toutes les cases sont initialisées avec la valeur s'obtient par Array.make_matrix s t v. Dans une matrice, les indices sont numérotés à partir de 0 . On accède au coefficient en position de la matrice par l'expression a.(i).(j), on le modifie par l'instruction a.(i).(j) <- v.
    - Écrire une fonction distance ( mot) ( mot) : int qui calcule par mémoïsation la distance dist( ).
Indication Ocaml : Nous rappelons la syntaxe de la fonction suivante :
  • List.filter, de type ('a -> bool) -> 'a list -> 'a list: la sous-liste des éléments de la liste tels que le prédicat vaut true s'obtient par filter .
    - Soit un entier. Exprimer la complexité en temps de la fonction distance b c en fonction des longueurs et des mots et . En déduire la complexité de l'instruction List.filter (fun c -> (distance b c) <= k) lc;; où est une liste de mots ciblés, chacun de longueur inférieure ou égale à , et où est un entier naturel.
10 - Soit la distance . Montrer qu'il existe un entier , des mots appartenant chacun à , des mots appartenant chacun à et des symboles , appartenant chacun à tels que
et

2 Fouille dans un trie

2.1 Représentation d'un corpus de mots par un trie

Définition : Un trie est un type particulier d'arbre dont chaque arête est orientée de la racine vers les feuilles et est étiquetée par un symbole de . Le trie vide est formé d'un seul sommet et de zéro arête. Lorsqu'une arête est étiquetée par le symbole , son extrémité finale doit être le trie vide. La taille d'un trie , notée , est le nombre de ses arêtes.
On dit qu'un mot appartient à un trie s'il existe un chemin, constitué de arêtes, issu de la racine et dont les arêtes successives ont pour étiquettes respectives les symboles et . Le symbole indique la présence d'un mot et joue le rôle de symbole terminateur.
Dans cette partie, les tries sont utilisés afin de représenter un corpus de mots ciblés.
Figure 1 - Exemple de trie de taille 28 contenant 9 mots.
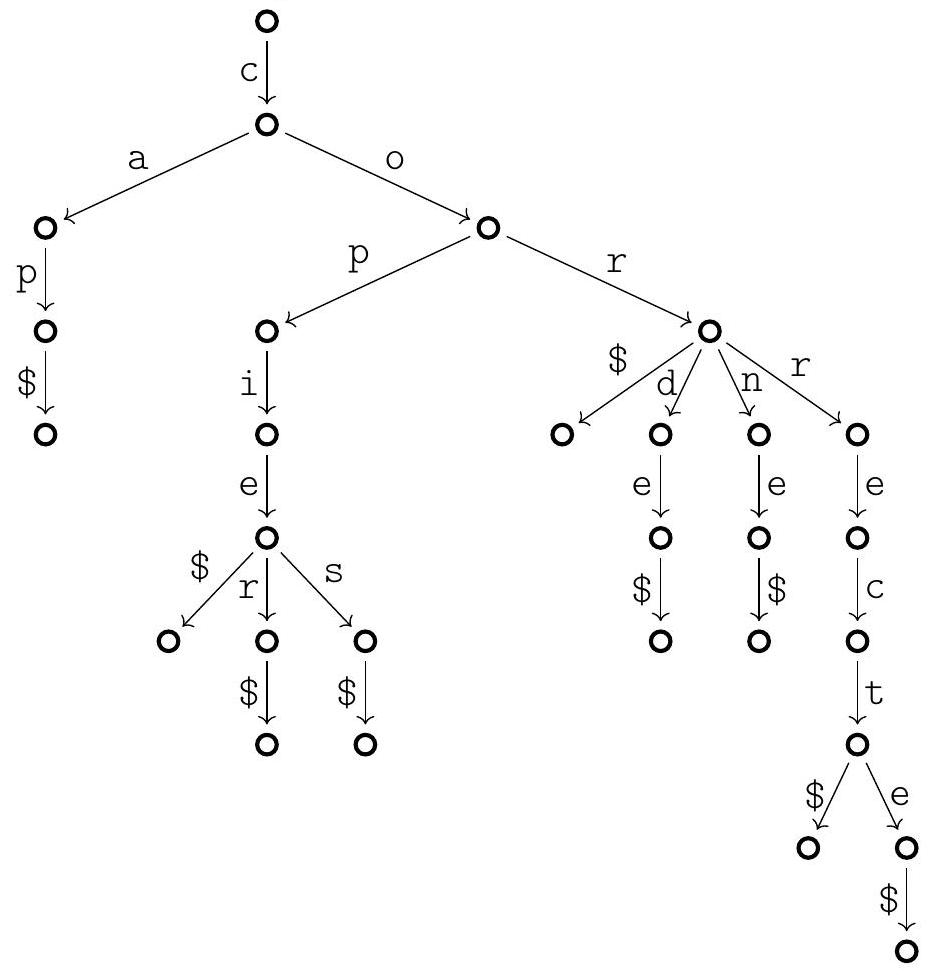
11 - Donner l'ensemble des mots du trie représenté à la figure 1.
Dans ce sujet, le terme dictionnaire désigne en général un type de données abstrait qui contient des associations entre une clé et une valeur.
12 - Nommer deux structures de données concrètes, qui réalisent le type abstrait dictionnaire. Pour chacune d'entre elles, rappeler sans justifier la complexité en temps de l'opération insertion.
Indication Ocaml : Nous définissons un type polymorphe 'a char_map qui réalise une structure de données persistante de dictionnaire associant des clés de type char à des valeurs de type quelconque 'a. Nous disposons de la constante et de la fonction suivante :
  • CharMap.empty, de type 'a char_map, qui désigne le dictionnaire vide.
  • CharMap.add, de type char -> 'a -> 'a char_map -> 'a char_map, telle que la valeur de retour de CharMap.add est un dictionnaire contenant les associations du dictionnaire ainsi qu'une association supplémentaire entre la clé et la valeur . Si la clé était déjà associée dans le dictionnaire , l'ancienne association de disparaît.
    Pour représenter les tries, nous définissons le type
    type trie Node of trie char_map ;;
    - Définir deux constantes trie_vide et trie_motvide, de type trie, qui réalisent respectivement le trie vide et le trie contenant le mot vide .
    - Écrire une fonction trie_singleton (x:char) : trie qui construit un trie contenant le mot formé d'un seul symbole .
Indication Ocaml: Nous utilisons un type polymorphe 'a option défini par
type 'a option =
| None
I Some of 'a;;
qui permet de représenter des valeurs de type 'a parfois non définies. Nous complétons le type 'a char_map par la fonction suivante :
  • CharMap.find, de type char -> 'a char_map -> 'a option, telle que l'appel de CharMap.find x d renvoie, en temps constant, Some t si la clé est associée à la valeur dans le dictionnaire et renvoie None s'il n'existe pas d'association de clé dans le dictionnaire .
    - Écrire une fonction trie_mem (c:mot) (Node tcm:trie) : bool qui teste si le mot appartient au trie Node tcm.
16 - Écrire une fonction trie_add (c:mot) (Node tcm:trie) : trie dont la valeur de retour est un trie contenant les mêmes mots que le trie Node tcm ainsi que le mot .
17 - Nous construisons le trie représenté à la figure 1 en déclarant d'abord la constante trie_vide (question 13), puis en appliquant neuf fois la fonction trie_add (question 16). Compte tenu du caractère persistant du type 'a char_map, combien d'exemplaires de trie_vide coexiste-t-il une fois la construction terminée? Expliquer.
Définition : Un trie est dit élagué si toute feuille est précédée d'une arête d'étiquette .
Indication Ocaml : Nous complétons le type 'a char_map par les fonctions suivantes : - CharMap.is_empty, de type 'a char_map -> bool, qui teste si un dictionnaire est le dictionnaire vide. CharMap.filter_map, de type (char -> 'a -> 'a option) -> 'a char_map -> 'a char_map, telle que CharMap.filter_map f d renvoie le dictionnaire $d^{\prime}$ restreint aux associations entre la clé $x$ et la valeur $t^{\prime}$ où, d'une part, il existe dans le dic- tionnaire $d$ une association entre la clé $x$ et la valeur $t$ et, d'autre part, $f(t)$ vaut Some tprime. Si le dictionnaire $d$ contient un couple clé et valeur $(x, t)$ mais que $f(t)$ vaut None, alors le dictionnaire $d^{\prime}$ ne contient pas d'association de clé $x$. En voici une illustration : $\begin{array}{|ccc|}d & x_{1} & \mapsto \\ & x_{2} & t_{1} \\ & x_{3} & \mapsto \\ & \vdots & t_{2} \\ & & t_{3} \\ & x_{1} & \mapsto \\ & & \\ x_{3} & \mapsto & t_{1}^{\prime} \\ \vdots & & \\ & & \end{array} \begin{aligned} & f\left(t_{1}\right)=\text { Some t1prime } \\ & f\left(t_{2}\right)=\text { None } \\ & f\left(t_{3}\right)=\text { Some t3prime }\end{aligned}$
18 - Compléter le code suivant afin que la valeur de retour de trie_trim t soit un trie élagué contenant les mêmes mots que le trie Node tcm.
let rec trie_trim (Node tcm:trie) : trie =
    let filtre (x:char) (y:trie) : trie option =
    (* a completer *)
    in
    Node(CharMap.filter_map filtre tcm);;

2.2 Filtrage dans un trie

19 - Soient un mot brouillé, un trie contenant un ensemble de mots ciblés et un entier naturel. On suppose avoir engendré la liste des mots de à distance inférieure ou égale à du mot . Montrer que la liste compte éléments. En déduire la complexité en temps de l'instruction List.filter (fun bb -> trie_mem bb t) lb;;.
Définition : Nous appelons système de transitions sur l'alphabet la donnée d'un triplet ( ) où
  • est un ensemble (fini ou non), dit ensemble des états,
    est un état, dit état initial,
  • est une relation, dite relation de transition.
Un mot est accepté par le système de transitions ( ) s'il existe une suite d'états telle que l'état égale l'état initial et, pour tout compris entre 0 et , le triplet ( ) appartient à la relation de transition .
On peut voir un système de transitions comme un automate éventuellement infini dont tous les états sont finals.
- Dessiner, sans justifier, un système de transitions fini qui accepte les mots n'ayant pas le mot ccmp comme facteur (c'est-à-dire que le mot n'est pas accepté si et seulement s'il contient quatre symboles consécutifs valant et p ).
Nous disons qu'un système de transitions ( ) est déterministe s'il existe une fonction partiellement définie telle que l'on ait
é
Nous notons alors ( ) ce système.
Indication Ocaml : Afin de représenter des systèmes de transitions déterministes, nous convenons de nous appuyer sur un type etat pour représenter l'ensemble des états . Ce type sera explicité ultérieurement. Nous déclarons
type syst_trans = etat -> char -> etat option; ;
pour représenter la fonction de transition . Pour tout couple , si delta est de type syst_trans, on accède à l'état image par l'expression delta qui vaut alors Some qprime si la transition est bien définie ou bien None si la transition n'est pas définie.
21 - Écrire une fonction trie_filter (qchapeau:etat) (delta:syst_trans) (Node tcm:trie) : trie qui renvoie un trie contenant les mots du trie Node tcm acceptés par le système de transitions déterministe ( ). Il n'est pas demandé de renvoyer un trie élagué.
22 - Un système de transitions déterministe ( ) étant fixé, quelle est la complexité en temps du calcul trie_filter qchapeau delta t en fonction du trie ? On suppose que l'exécution de la fonction de transition s'effectue en temps constant.

3 Système de transitions des voisins d'un mot brouillé

Dans toutes les questions restantes, les lettres et désignent systématiquement deux mots de longueur et de . La lettre désigne un entier naturel. L'écriture désigne la concaténation du mot et du symbole ; nous parlons alors de mot prolongé.
L'objectif de cette section est de construire un système de transitions non déterministe qui, à partir d'un entier naturel et d'un mot brouillé , accepte n'importe quel préfixe du mot prolongé où est un mot de tel que et aucun autre mot n'est accepté.
Définition : Nous appelons transformations élémentaires les ( ) appellations suppr, subs et -ins-puis-id, avec ; nous notons leur ensemble.
Soient un mot de longueur et un mot de longueur . Nous disons qu'une suite de transformations élémentaires est un script de transformation du mot en le mot s'il existe une factorisation du mot telle que pour tout entier compris entre 1 et ,
(1) est un mot de ,
(2) lorsque suppr, alors le mot est le mot vide ,
(3) lorsque subs, alors le mot est de longueur 1 et, en l'identifiant à un symbole, il est distinct du symbole ,
(4) lorsque -ins-puis-id, alors le mot est de longueur et le dernier symbole de vaut le symbole .
Nous observons que la factorisation du mot en est unique et ne dépend que du script .
Voici un exemple de script de transformation entre le mot correct et le mot incorekte .
C 0 r r e C t $
inc 0 e k 七 e$
2-ins-puis-id 0-ins-puis-id 0-ins-puis-id suppr 0-ins-puis-id subs 0-ins-puis-id 1-ins-puis-id
Définition : Le coût d'une transformation élémentaire est précisé par le tableau suivant :
Transformation élémentaire suppr subs -ins-puis-id
Coût 1 1
Le coût d'un script de transformation est la somme des coûts des transformations élémentaires constituant le script.
Dans l'exemple ci-dessus, le coût du script vaut 5 (ou encore ).
Définition : Nous utilisons le terme -script pour raccourcir l'expression «script de transformation de coût inférieur ou égal à ».
- Montrer que la distance dist ( ) est inférieure ou égale à si et seulement s'il existe un -script du mot prolongé vers le mot prolongé .
Dans les questions 24 et 25 , la lettre désigne un entier avec et un -script depuis le préfixe préf du mot prolongé vers un certain préfixe du mot prolongé . On appelle le suffixe de tel que se factorise en .
- Si l'on a , par quelles appellations est-il possible de compléter le -script pour que ( ) soit un -script depuis le préfixe préf vers un certain préfixe du mot prolongé ? On exprimera sa réponse en fonction du symbole de , du suffixe et du coût du script .
25 - Si l'on a , par quelles appellations et sous quelles conditions est-il possible de compléter le -script pour que ( ) soit un -script depuis le mot prolongé vers le mot prolongé ?
Indication Ocaml : Nous précisons le type etat en déclarant type etat = mot * int;;
- Le mot brouillé étant toujours fixé, décrire en OCaml un système de transitions ( ) qui accepte tout préfixe du mot , avec , tel que et qui n'accepte aucun autre mot. On définira une fonction etat_initial (b:mot) (k:int) : etat qui construit l'état initial et une fonction delta (k:int) (q:etat) (x:char) : etat list qui renvoie la liste des états tels que l'on ait .
- Comment adapter la fonction trie_filter, écrite à la question 21, pour qu'elle fonctionne avec le système de transitions de la question 26 ? On ne demande pas de code. Préciser la complexité en temps. Pourquoi peut-on souhaiter adapter la fonction trie_filter plutôt que de déterminiser le système de transitions?

Fin de l'épreuve

Mines Option Informatique MP 2022 - Version Web LaTeX | WikiPrépa | WikiPrépa