Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE I -PSI
L'énoncé de cette épreuve, particulière aux candidats de la filière PSI, comporte 7 pages.

Abstract

- Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Tout résultat fourni dans l'énoncé peut être utilisé pour les questions ultérieures, même s'il n'a pas été démontré.
Il ne faudra pas hésiter à formuler les commentaires (incluant des considérations numériques) qui vous sembleront pertinents, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.

Notations : vecteur

(gras); vecteur unitaire pour la coordonnée

UTILISATION DES INDUCTEURS EN MÉTALLURGIE

La production d'un champ magnétique variable à l'aide d'un inducteur est très répandue en métallurgie ; elle intervient dans des phases très diverses telles que la circulation, le brassage, la fusion ou la confection des lingots. Ce problème concerne principalement la fusion d'un alliage d'aluminium et sa confection en lingots. Il comprend deux parties, largement indépendantes entre elles, pour ce qui est de leur traitement.

La relation vectorielle suivante sera utile pour la résolution :

Fusion du métal à l'aide d'un four à induction à creuset

Le four est constitué (figure 1) d'un creuset cylindrique (rayon

, hauteur

) qui contient l'alliage à fondre et d'un inducteur composé d'un solénoïde monocouche (considéré
comme infiniment long) parcouru par un courant d'intensité variable

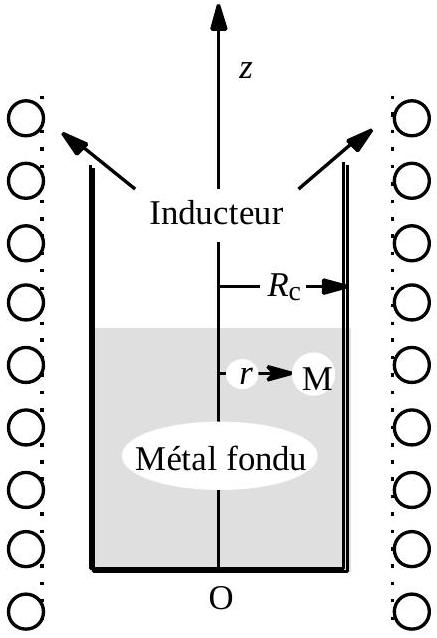
. L'action du champ magnétique variable sur le métal consiste d'une part en un effet thermique (fusion puis maintien à l'état liquide de l'alliage), d'autre part en un effet mécanique (mise en mouvement du bain métallique).

Fig. 1 : four à induction

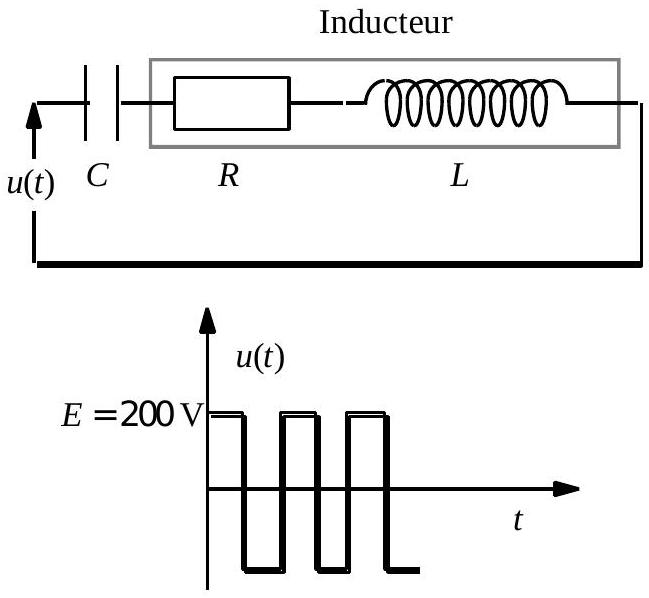
Fig. 2 : schéma équivalent de l'inducteur

è

partie : Étude de l'alimentation de l'inducteur à vide.

Alimentation directe par une source de tension alternative " symétrique "
L'inducteur est équivalent à un circuit série composé d'une inductance

et d'une résistance

; afin de diminuer l'impédance du circuit on ajoute en série un condensateur de capacité

. La tension

appliquée est un créneau alternatif " symétrique ", d'amplitude

et de fréquence 1000 Hz ( figure 2).

Le développement en série de Fourier de la tension

est

- Calculer les valeurs efficaces

de l'harmonique

et de l'harmonique

de la tension

- Calculer les modules des impédances de l'inducteur,

, relatives aux harmoniques 1 et 3 ; en déduire les valeurs efficaces

des intensités des courants correspondants et montrer que l'intensité

dans l'inducteur est pratiquement sinusoïdale.

Conventions pour le thyristor

La tension

est fournie par un onduleur, alimenté par un générateur continu de f.e.m

, constitué de quatre interrupteurs électroniques

. Chaque interrupteur est constitué par un thyristor et une diode supposés parfaits et montés en antiparallèle (figure 3). Le thyristor (fig. ci-contre) est un interrupteur commandé qui laisse passer le courant uniquement lorsque l'intensité qui le traverse est positive (sens direct) et qui bloque le courant lorsque l'intensité est négative (sens inverse)

Les quatre interrupteurs fonctionnent simultanément deux à deux c'est-à-dire que pendant une demi-période de fonctionnement les interrupteurs

sont fermés alors que les interrupteurs

sont ouverts ; la demi-période suivante

sont ouverts alors que les interrupteurs

sont fermés.

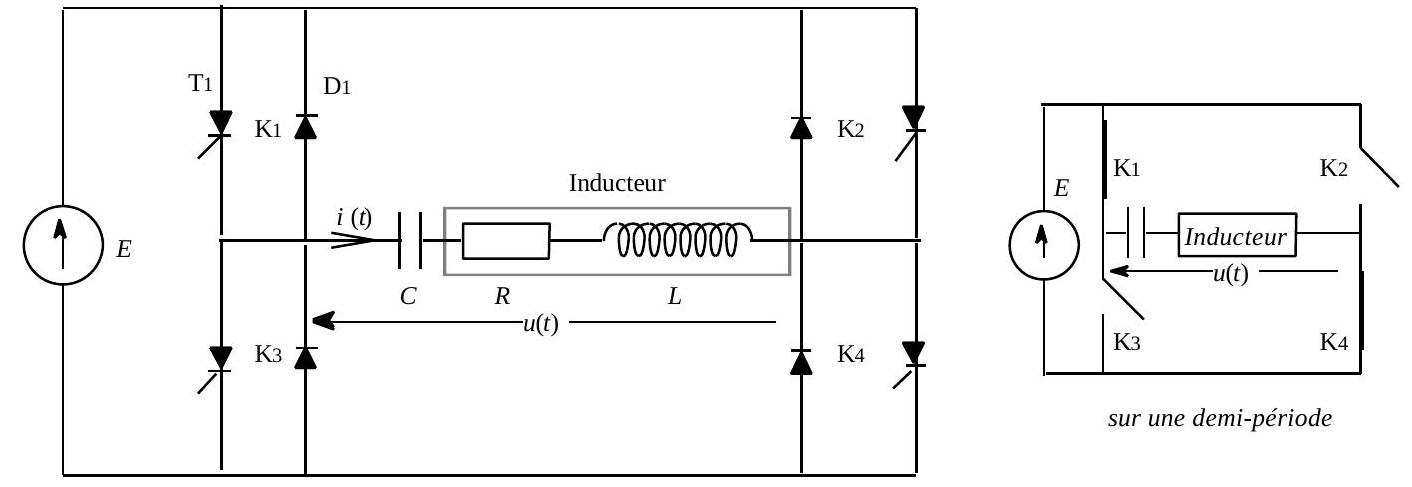
Fig. 3 : onduleur

3 - On suppose que le courant dans l'inducteur est sinusoïdal et de la forme

La tension

est identique à celle qui est représentée à la figure 2. Représenter les intensités

, qui traversent respectivement le thyristor

, la diode

et le générateur de f.e.m

, en fonction du temps.

- Calculer les valeurs moyennes de ces trois intensités.

- En déduire la puissance moyenne fournie par la source de tension.

è

partie : Étude des paramètres électromagnétiques à l'intérieur du métal
fondu.

6 - Décrire les phénomènes dont le métal est le siège et qui permettent éventuellement sa fonte.
- On suppose dans cette $è$ partie que l'inducteur est parcouru par un courant
d'intensité avec une fréquence . On utilise la base relative aux coordonnées cylindriques ( ), ( ). La masse de l'alliage d'aluminium est le siège de courants induits dont le vecteur complexe densité de courant au point M du métal, à la distance de l'axe Oz est de la forme . Dans l'hypothèse où le champ magnétique à l'intérieur du métal n'est fonction que de la variable , justifier cette orientation du vecteur densité de courant .
- L'alliage d'aluminium étudié est considéré comme un conducteur, électriquement neutre, défini par les constantes du vide et par sa conductivité . On admettra que la vitesse locale du bain métallique est suffisamment petite pour que l'on puisse négliger le terme dans la relation liant la valeur locale de la densité de courant aux champs électrique et magnétique : . Montrer alors que, pour la fréquence utilisée, on peut négliger le courant de déplacement.
- Notant l'opérateur laplacien vectoriel, montrer que le vecteur densité de courant vérifie l'équation différentielle et en déduire l'équation différentielle du second ordre vérifiée par la fonction complexe ; ce sera l'équation (1).

10 - Exprimer (1) en termes des grandeurs réduites

(ce sera l'équation 1'), calculer la valeur numérique de

11 - On se propose d'exprimer une solution approchée de l'équation (1') pour une épaisseur de bain métallique de l’ordre de

au voisinage de la périphérie

. Posant dans (1')

, admettant que, dans l'équation différentielle relative à la fonction

ainsi obtenue il soit légitime de négliger le terme en

, admettant enfin que la fonction

est paire, établir une forme approchée de la solution au voisinage de la périphérie du creuset. Préciser la signification de

- Exprimer la puissance moyenne

dissipée par effet Joule à l'intérieur du volume du bain métallique ; quelle donnée faudrait-il connaître pour déterminer complètement la solution ? Pour améliorer l'efficacité calorifique du four vaut-il mieux utiliser un courant d'alimentation de l'inducteur de fréquence faible ou de fréquence élevée ?

Confection des lingots d'alliages légers : "coulée électromagnétique"

Au cours d'une coulée classique on utilisait jusqu'en 1973 une lingotière pour donner sa forme au lingot (métal solide). Ce procédé a été abandonné au profit de la coulée électro
magnétique, inventée en U.R.S.S. par Getselev & al : dans ce procédé, le maintien réalisé jadis par la paroi matérielle de la lingotière est assuré par des forces électromagnétiques de volume. Ces forces sont produites par une spire inductrice alimentée par un courant électrique sinusoïdal de forte intensité (de l’ordre de 5000 A ) et de fréquence voisine de 2000 Hz (figure 4). Le refroidissement qui permet le changement d'état de l'alliage d'aluminium est assuré par un jet d'eau dirigé sur la paroi latérale du lingot.

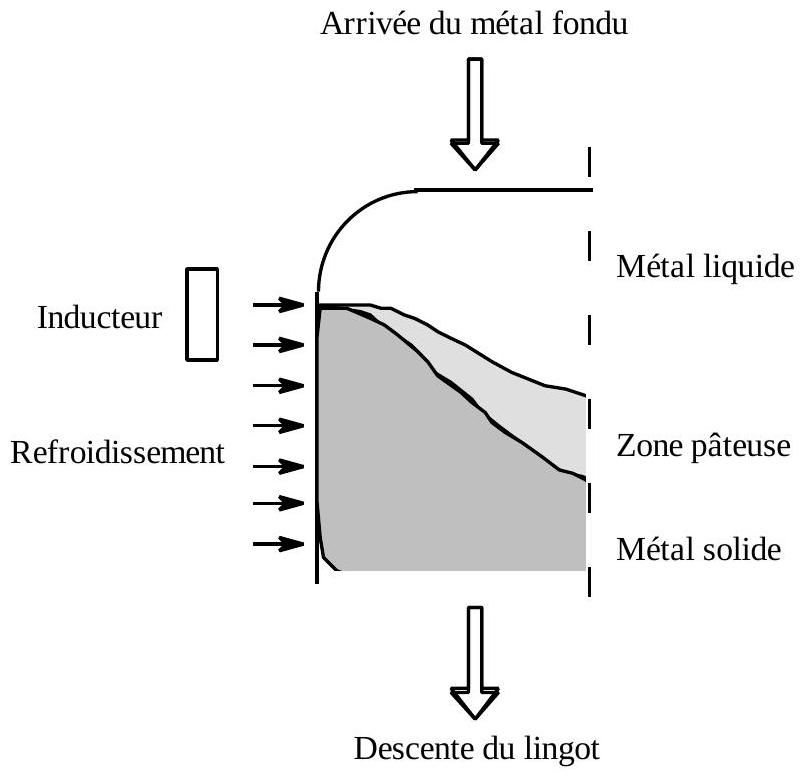
Fig. 4 : principe de la coulée électromagnétique

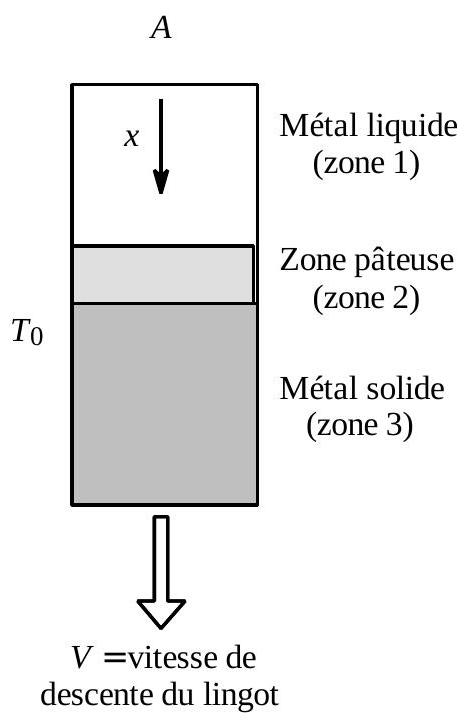
Fig. 5 : modèle de la coulée

$è$ partie : Étude des transferts thermiques.

Afin de pouvoir effectuer une étude plus aisée des transferts thermiques on adopte le modèle simplifié (fig. 5) où les formes des différentes phases du métal dans le lingot (liquide, pâteuse, solide) sont considérées comme cylindriques, et de rayon

. La conductivité thermique du métal liquide est notée

, celle du métal solide est notée

; ces grandeurs sont supposées indépendantes de la température. Par l'intermédiaire d'une goulotte non représentée sur la figure 5, le métal, fondu au préalable dans un four à creuset, arrive en A avec une vitesse négligeable. Sa température

est uniforme et très largement supérieure à la température

du jet de refroidissement latéral. On appelle

le flux thermique qui traverse la section

à l'abscisse

; on pose

. On fera l'hypothèse que la vitesse du métal (liquide ou solide) est nulle (ce qui est pratiquement le cas lorsque la vitesse de descente

du lingot ainsi que la vitesse de brassage à l'intérieur du bain métallique sont très faibles).

- Écrire la loi de Fourier qui traduit le transfert thermique par conduction dans les zones (1) et (3) (direction

). Déduire une relation entre

et les paramètres

pour la zone (1); on aura une relation identique pour la zone (3).

-Les pertes thermiques dues au refroidissement sont supposées proportionnelles à la surface d'échange entre le métal et le milieu extérieur ainsi qu'à l'écart de température entre le métal et le milieu extérieur; on appelle

le coefficient de proportionnalité (ce coef
ficient est considéré comme constant quel que soit l'état du métal). En considérant le bilan thermique sur une longueur

infiniment petite du métal, trouver une relation entre

-Déduire des questions (13) et (14) les équations différentielles en

; on posera

16 - Les fonctions

seront labellées

dans la zone 1 (métal liquide) et

dans la zone 3 (métal solide). Le changement d'état du métal se fait dans la zone pâteuse (zone 2) ; la hauteur

de la colonne de métal liquide est

. Donner les expressions formelles puis numériques de

et de

. Représenter sommairement la fonction

- La vitesse de descente du lingot est notée

; la hauteur de la zone pâteuse est notée

et la température

dans cette zone est uniforme. La masse volumique du métal est notée

et sa chaleur latente de fusion

. Donner, formellement puis numériquement, l'expression de

, sachant que, la longueur du lingot étant très grande, la fonction

ne diverge pas lorsque

tend vers l'infini. Données numériques :

18 -On suppose dans cette question que l'on façonne, toujours par la méthode de coulée électromagnétique, un lingot de petit diamètre

; la vitesse de descente du lingot par rapport au repère du laboratoire n'est plus négligeable :

capacité thermique massique du métal solide est

, sa masse volumique est

). Ces deux grandeurs sont considérées comme indépendantes de la température. Écrire pour la zone (3) c’est-à-dire la zone du métal solide, l’équation traduisant le bilan thermique local en régime stationnaire, les conditions de refroidissement étant inchangées (on fera ce bilan sur une tranche de métal d'épaisseur d

et d'abscisse

- Déduire le champ de températures

de la zone (3) en régime stationnaire si on admet que

et que la longueur du lingot est grande devant

20 -Simplifier l'expression de

dans le cas où

; calculer numériquement cette condition sur

- Calculer la puissance thermique perdue par la partie solide du métal (on considérera que la longueur

du lingot est grande devant

). Commenter le résultat et effectuer l'application numérique.

2ème partie : Étude des paramètres électromagnétiques.

22 - On désire mesurer la valeur locale du champ magnétique à l’intérieur du métal liquide à l'aide d'un capteur; quel type de capteur utiliseriez-vous ? quel en serait son principe?

23 -On désire mesurer la valeur du champ électrique à l'intérieur du bain métallique à l'aide d'un capteur ; quel type capteur utiliseriez-vous? quel en serait son principe?

24 - Si l'on considère que les vitesses locales du métal fondu sont pratiquement nulles, quelles autres grandeurs physiques les mesures précédentes permettent-elles d'atteindre?

FIN DU PROBLÈME
FIN DE L'ÉPREUVE

Mines Physique 1 PSI 2000

A 00 PHYS. I

PREMIÈRE ÉPREUVE DE PHYSIQUE