Dans ce sujet, on s'intéresse à des textes de grande taille auxquels plusieurs auteurs apportent des modifications au cours du temps. Ces textes peuvent par exemple être des programmes informatiques développés par de multiples auteurs. Il est important de pouvoir efficacement gérer les différentes versions de ces programmes au cours de leur développement et limiter le stockage et la transmission d'informations redondantes. Nous allons pour cela nous intéresser à une notion de différentiels entre textes.

Complexité. La complexité, ou le temps d'exécution, d'une fonction

est le nombre d'opérations élémentaires (addition, multiplication, affectation, test, etc...) nécessaires à l'exécution de

dans le cas le pire. Lorsque la complexité dépend d'un ou plusieurs paramètres

, on dit que

a une complexité en

s'il existe une constante

telle que, pour toutes les valeurs de

suffisamment grandes (c'est-à-dire plus grandes qu'un certain seuil), pour toute instance du problème de paramètres

, la complexité est au plus

Lorsqu'il est demandé de donner la complexité d'un programme, le candidat devra justifier cette dernière si elle ne se déduit pas directement de la lecture du code.

Rappels concernant le langage Python. Ce sujet utilise les types Python listes et dictionnaires, mais seules les opérations mentionnées ci-dessous sont autorisées dans vos réponses. Quand une complexité est indiquée avec un symbole (*), cela signifie que nous faisons une hypothèse simplificatrice sur sa complexité. La justification de cette simplification est hors-programme.

désignent des listes en Python :

len (1) renvoie la longueur de la liste 1 , c'est-à-dire le nombre d'éléments qu'elle contient. Complexité en .
11 == 12 teste l'égalité des listes 11 et 12 . Complexité en avec le minimum de len(l1) et len(l2).
1 [i] désigne le i-ème élément de la liste 1 , où l'indice i est compris entre 0 et len (l)-1 Complexité en .
1 [i:j] construit la sous-liste [1 [i], ..., l[j-1]]. Complexité en . L'usage des variantes à la place de , et de à la place de est aussi autorisé.
l. append(e) modifie la liste l en lui ajoutant l'élément e en dernière position. Complexité en .
l.pop() renvoie le dernier élément de la liste l (supposée non vide) et supprime l'occurrence de cet élément en dernière position dans la liste. Complexité en .

On pourra aussi utiliser la fonction range pour réaliser des itérations.
Si d est un dictionnaire Python :

{key_1: v_1, . . . , key_n: v_n} crée un nouveau dictionnaire en associant chaque valeur v_i à une clé key_i. Complexité en .
d[key] renvoie la valeur associée à la clé key dans d et lève une erreur si la clé key n'est pas présente. Complexité en .
d [key] modifie d pour associer la valeur v à la clé key, même si la clé key n'est pas présente dans d initialement. Complexité en .
key in d teste si la clé key est présente dans d. Complexité en .

Sauf mention contraire, les fonctions à écrire ne doivent pas modifier leurs entrées.

La structure de données texte. Dans ce sujet, on appelle texte une liste de caractères. Par exemple, ['b', 'i', 'n', 'g', 'o'] est un texte de longueur 5.

Partie I : Différentiels par positions fixes

Dans cette partie, nous traitons le problème avec une hypothèse simplificatrice : les textes comparés ont toujours la même taille.

Question 1. Sans utiliser le test

sur les listes, écrire une fonction textes_égaux(texte1, texte2) qui teste si deux textes sont égaux. Donner la complexité de cette fonction.

Exemples

>>> textes_égaux(['v', 'i', 's', 'a'], ['v', 'a', 'i', 's'])
False
>>> textes_égaux(['v', 'i', 's', 'a'], ['v', 'i', 's', 'a'])
True

Dans la suite de ce sujet, on pourra utiliser == sur les listes plutôt que cette fonction.

Si deux textes ne sont pas égaux mais ont la même longueur

, on souhaite compter le nombre de positions qui diffèrent, c'est à dire déterminer combien il existe de positions

telles que les caractères en position

sont différents dans les deux textes.

Question 2. Écrire une fonction distance(texte1, texte2) qui calcule cette quantité. On supposera que les deux textes ont le même nombre de caractères. Donner la complexité de cette fonction.

Exemples

>>> distance(['v', 'i', 's', 'a'], ['v', 'a', 'i', 's'])
3
>>> distance(['a', 'v', 'i', 's'], ['v', 'i', 's', 'a'])
4

Question 3. En vous aidant d'un dictionnaire dont les clés sont des caractères, écrire une fonction aucun_caractère_commun(texte1, texte2) qui renvoie True si et seulement si l'ensemble des caractères qui apparaissent dans texte1 est disjoint de l'ensemble des caractères qui apparaissent dans texte2. Les deux textes peuvent avoir ici des longueurs différentes. Cette fonction devra avoir une complexité

texte 1

texte 2

Exemples

>>> aucun_caractère_commun(['a', 'v', 'i', 's'], ['v', 'i', 's', 'a'])
False
>>> aucun_caractère_commun(['a', 'v', 'i', 's'], ['u', 'r', 'n', 'e'])
True

Nous introduisons maintenant une structure de données spécifique pour représenter un différentiel par positions fixes entre deux textes.

La Figure 1 présente un exemple de couple de textes (texte

, texte

) qui diffèrent sur 4 tranches (représentées par des zones grisées sur la figure). En dehors des tranches, les textes sont égaux.

Figure 1 - Exemple de couple ( texte

, texte

) dont on veut calculer le différentiel (sur des positions fixes).

La structure de données tranche. Une tranche est un dictionnaire avec trois clés 'début', 'avant' et 'après'. La valeur associée à la clé 'début' est le premier indice de la tranche, les
textes associés aux clés 'avant' et 'après' représentent les textes (de même longueur) de la tranche avant et après modification. Dans la suite de cette partie, on s'appuiera sur les fonctions suivantes pour manipuler cette structure.

def tranche(arg_début, arg_avant, arg_après):
    return {'début': arg_début, 'avant': arg_avant, 'après': arg_après}
def début(tr):
    return tr['début']
def après(tr):
    return tr['après']
def avant(tr):
    return tr['avant']
def fin(tr):
    return début(tr) + len(après(tr))

Nous ne fournissons pas de fonction pour modifier une tranche car nous souhaitons traiter cette structure de données comme une structure immuable

On peut représenter le différentiel de la Figure 1, par la liste suivante :

[
    tranche(3, ['g', 'r', 'a', 'n', 'd'], ['p', 'e', 't', 'i', 't']),
    tranche(11, ['â', 't', 'e', 'a', 'u'], ['i', 'e', 'n', ', 'a']),
    tranche(17, ['f'], ['s']),
    tranche(19, ['r', 't'], ['i', 'f'])
]

La structure de données différentiel. Un différentiel est une liste (potentiellement vide) de tranches

représentant des modifications touchant des zones distinctes d'un texte, telle que

début
pour tout , pour tout , avant

Existence et unicité d'un différentiel par positions fixes. Pour deux textes texte

et texte

de même longueur

, il existe un unique différentiel

tel que :

si , alors début et
pour tout , texte début
pour tout , texte début
pour tout , si début , alors texte texte

Cet unique différentiel est appelé le différentiel de texte

vis-à-vis de texte

Toutes les propriétés précédentes sur les différentiels assurent les propriétés intuitives suivantes :

les tranches sont présentées par indices de début croissants, sans se chevaucher, ni se toucher ;
chaque tranche tr couvre un intervalle de positions [début(tr), fin(tr) - 1] sur lequel texte et texte diffèrent à chaque position, et dont les sous-textes sur ces intervalles correspondent à avant(tr) pour texte et après(tr) pour texte .

Question 4. Écrire une fonction différentiel(texte1, texte2) qui calcule le différentiel du texte texte2 vis-à-vis du texte texte1, supposés de même longueur. La complexité attendue est

texte1

. Justifier cette complexité.

Question 5. Écrire une fonction applique(texte1, diff) qui, étant donné un texte texte1 et un différentiel diff, renvoie un texte texte2 tel que diff soit le différentiel de texte2 vis-à-vis de texte1. On supposera que le différentiel diff contient des tranches cohérentes avec la taille et le contenu du texte texte1. Donner et justifier la complexité.

Pour reconstruire l'ancienne version d'un texte à partir d'un différentiel, nous allons nous appuyer sur la notion de différentiel inversé.

Question 6. Écrire une fonction inverse(diff) telle que pour tous textes texte1, texte2 de même longueur, si diff désigne différentiel(texte1, texte2), alors applique(texte2, inverse(diff)) = texte1 et inverse(inverse(diff)) = diff. Donner sa complexité.

La structure de données texte versionné. Nous représentons un texte versionné par un dictionnaire contenant la version courante du texte, comme valeur associée à la clé 'courant', et l'historique des différentiels qui ont mené jusqu'à cette version dans une pile

de différentiels associée à la clé historique. Dans la suite de cette partie, on s'appuiera sur les fonctions suivantes pour manipuler cette structure.

def versionne(texte):
    return {'courant' : texte, 'historique' : [] }
def courant(texte_versionné):
    return texte_versionné['courant']
def remplace_courant(texte_versionné, texte):
    texte_versionné['courant'] = texte
def historique(texte_versionné):
    return texte_versionné['historique']

Contrairement à la structure immuable de tranche, nous nous autorisons cette fois à modifier la structure de texte versionné, en particulier la pile qu'elle contient via les opérations historique(texte_versionné).append(diff) et historique(texte_versionné).pop().

Question 7. Écrire les fonctions modifie(texte_versionné, texte) et annule(texte_versionné) qui assurent les deux opérations de base attendues sur un texte versionné texte_versionné. La fonction modifie(texte_versionné, texte) modifie texte_versionné pour lui ajouter une nouvelle version correspondant au texte texte, en supposant qu'il a la même longueur

que le texte courant. La taille de l'historique augmente alors de 1. La fonction ne renvoie rien. La fonction annule(texte_versionné) modifie texte_versionné en annulant l'effet de la dernière modification effectuée et renvoie la nouvelle valeur courante du texte. La taille de l'historique diminue alors de 1 . On suppose que la pile des différentiels n'est pas vide lors de cet appel. Donnez les complexités de ces deux fonctions.

Exemples

>>> texte_versionné = versionne(['a', 'v', 'i', 's'])
>>> modifie(texte_versionné, ['v', 'i', 's', 'a'])
>>> modifie(texte_versionné, ['v', 'i', 't', 'a'])
>>> modifie(texte_versionné, ['l', 'i', 's', 'a'])
>>> assert courant(texte_versionné) == ['l', 'i', 's', 'a']
>>> assert historique(texte_versionné) == [
    différentiel(['a', 'v', 'i', 's'], ['v', 'i', 's', 'a']),
    différentiel(['v', 'i', 's', 'a'], ['v', 'i', 't', 'a']),
    différentiel(['v', 'i', 't', 'a'], ['l', 'i', 's', 'a'])
]
>>> annule(texte_versionné)
['v', 'i', 't', 'a'])
>>> annule(texte_versionné)
['v', 'i', 's', 'a'])
>>> annule(texte_versionné)
['a', 'v', 'i', 's']

Partie II : Différentiels sur des positions variables

Dans cette partie, nous nous intéressons à des différentiels de textes dont les longueurs ne sont plus forcément égales. Nous adaptons pour cela la définition de tranche et de différentiel. La Figure 2 présente un exemple de couple ( texte

, texte

) dont on va représenter le différentiel par une liste de tranches (représentées par des zones grisées sur la figure). Cette fois, les tranches désignent des portions de textes qui ne sont pas nécessairement de la même longueur, ni alignées.

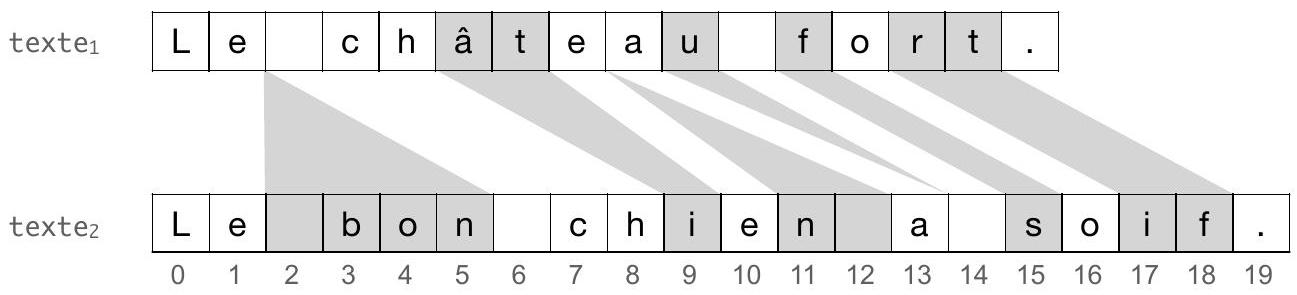
Figure 2 - Exemple de couple (texte

, texte

) dont on veut calculer le différentiel sur des positions variables.

Nouvelle structure de données tranche. Un différentiel d'un texte texte

vis-à-vis d'un texte texte

est toujours une liste de tranches mais chaque tranche comporte maintenant 4 clés:

la clé 'début_avant' représente la position d'un sous-texte avant qui a été supprimé de texte ;
la clé 'avant' est associée au texte avant;
la clé 'début_après' représente la position dans texte d'un sous-texte après, qui a été ajouté à la place du sous-texte avant en position dans texte ;
la clé 'après' est associée au texte après.

Dans la suite de cette partie, on s'appuiera sur les fonctions suivantes pour manipuler cette structure.

def tranche(arg_début_avant, arg_avant, arg_début_après, arg_après):
    return {'début_avant': arg_début_avant,
        'avant': arg_avant,
        'début_après': arg_début_après,
        'après': arg_après}
def début_avant(tr):
    return tr['début_avant']

def début_après(tr):
    return tr['début_après']
def après(tr):
    return tr['après']
def avant(tr):
    return tr['avant']
def fin_avant(tr):
    return début_avant(tr) + len(avant(tr))
def fin_après(tr):
    return début_après(tr) + len(après(tr))

Nouvelle structure de données différentiel. Un différentiel est une liste (potentiellement vide) de tranches [

] telle que

début_avant fin_avant début_avant fin_avant
début_après après début_après fin_après
pour tout , aucun_caractère_commun(avant , après True
pour tout ou len(après

Notion de différentiel valide vis-à-vis de deux textes. Pour deux textes texte

et texte

de même longueur

, un différentiel valide de texte

vis-à-vis de texte

est une liste diff

de tranches telle que :

si , alors début_avant et avant
si , alors début_après et après
pour tout , texte [début_avant fin_avant
pour tout , texte [début_après : fin_après après
pour tout , les sous-textes texte 1 [fin_avant tr : début_avant tr et texte fin_après tr : début_après tr sont égaux
si alors les textes texte et texte sont égaux
si alors texte début_avant début_après et

On peut représenter le différentiel de la Figure 2, par la liste suivante :

[
    tranche( 2, [], 2, [' ', 'b', 'o', 'n']),
    tranche( 5, ['â', 't'], 9, ['i']),
    tranche( 8, [], 11, ['n', ']),
    tranche( 9, ['u'], 14, []),
    tranche(11, ['f'], 15, ['s']),
    tranche(13, ['r', 't'], 17, ['i', 'f'])
]

On admet que, comme dans la partie précédente, on peut écrire des fonctions applique et inverse satisfaisant les mêmes propriétés que précédemment sur cette nouvelle notion de différentiel. On définit le poids d'un différentiel comme la somme des longueurs des sous-textes avant(tr) et après(tr) pour toutes les tranches tr qui le composent.

Question 8. Écrire une fonction poids(diff) qui calcule le poids d'un différentiel diff. Donner sa complexité.

Exemple

>>> poids([tranche(0, ['b'], 0, ['t', 'r', 'o', 't', 't']),
    tranche(2, ['c', 'y', 'c', 'l'], 6, ['n'])])
1 1

On s'intéresse à la distance d'édition

entre deux textes. Dans ce sujet, on définit cette distance comme le nombre minimal de suppressions et d'insertions de caractères pour passer d'un texte à un autre. On peut facilement se convaincre que cette distance coïncide avec le poids minimal possible pour un différentiel entre les deux textes.

Nous allons calculer cette distance par programmation dynamique. Pour deux textes texte

et texte

fixés, et pour

texte

, on note

la distance d'édition pour passer de

. La matrice

est appelée matrice de distance d'édition entre texte

et texte

La Figure 3 présente la matrice

pour texte

et texte

Question 9. Donnez une équation de récurrence qui exprime

en fonction de

, texte

et texte

, pour

texte

len(texte

). Justifier brièvement la validité de cette équation, sans rédiger une preuve complète.

Question 10. Écrire une fonction levenshtein(texte1, texte2) de complexité polynomiale qui renvoie la matrice

. Préciser sa complexité.

On utilisera l'instruction

for

in range

for

in range

pour initialiser une matrice

lignes et

colonnes avec des zéros.

F	U		A	B	C	C	Y		Z
	0	1	2	3	4	5	6	7	8
	1	2	1	2	3	4	5	6	7
	2	3	2	1	2	3	4	5	6
	3	4	3	2	1	2	3	4	5
	4	5	4	3	2	3	4	5	6
	5	6	5	4	3	2	3	4	5
	6	7	6	5	4	3	4	5	6
	7	8	7	6	5	4	5	6	7

Figure 3 - Exemple de matrice de distance d'édition

Question 11. Écrire une fonction différentiel(texte1, texte2, M) qui calcule un différentiel du texte texte2 vis-à-vis du texte texte1, en s'aidant de la matrice de distance

donnée par levenshtein(texte1, texte2). Le différentiel renvoyé doit être de poids minimal. La fonction devra avoir une complexité

texte1

texte2

. Justifier cette complexité et expliquer brièvement pourquoi le différentiel calculé satisfait les propriétés attendues par un différentiel. On pourra s'aider de la Figure 3 pour comprendre quel parcours suivre dans la matrice M.

Si on se place dans un scénario de travail collaboratif où deux auteurs différents modifient en parallèle le même texte texte, il est nécessaire de pouvoir fusionner leur travail. Nous notons texte1 le nouveau texte obtenu après le travail du premier auteur sur texte et diff1 le différentiel correspondant. De même, nous notons texte2 le texte obtenu après le travail du deuxième auteur sur le même texte texte, et diff2 le différentiel correspondant.

Exemple

>>> texte =
    ['l', 'e', ', 'c', 'h', 'a', 't', ', 'a', ', 's', 'o', 'i', 'f']
>>> texte1 =
    ['l', 'e', ', 'c', 'h', 'a', 't', ', 'a', ', 't', 'r', 'è', 's',
    , ', 's', 'o', 'i', 'f']
>>> texte2 =
    ['l', 'e', ' ', 'c', 'h', 'i', 'e', 'n', ', 'a', ', 's', 'o', 'i', 'f']
>>> diff1 = différentiel(texte, texte1, levenshtein(texte, texte1))
>>> assert diff1 == [tranche(9, [], 9, [' ', 't', 'r', 'è', 's'])]
>>> diff2 = différentiel(texte, texte2, levenshtein(texte, texte2))
>>> assert diff2 == [tranche(5, ['a', 't'], 5, ['i', 'e', 'n'])]

Pour fusionner le travail des deux auteurs, on apporte des modifications à diff2 de façon à ce que le texte final, qui inclut les modifications des deux auteurs, soit exprimable comme l'application du différentiel diff1, puis de la nouvelle version de diff2 sur le texte initial. Dans l'exemple précèdent, le texte final attendu est : ['l', 'e', ' ', 'c', 'h', 'i', 'e', 'n', ' ', 'a', ', 't', 'r', 'è', 's', ', 's', 'o', 'i', 'f'].

Nous allons être prudents en nous assurant au préalable que les modifications apportées ne concernent pas les même zones du texte initial.

Question 12. Écrire une fonction conflit(diff1, diff2) qui prend en argument deux différentiels diff1 et diff2 et renvoie True si et seulement s'il existe une tranche tr

dans diff1 et une tranche

dans diff2 telles que

é é

Cette fonction devra avoir une complexité

que l'on justifiera.
Question 13. Écrire une fonction fusionne(diff1, diff2) qui renvoie un nouveau différentiel représentant la mise à jour de diff2. Il est attendu que poids(fusionne(diff1, diff2))= poids(diff2). On suppose que les deux différentiels diff1 et diff2 ne sont pas en conflit. Cette fonction devra avoir une complexité

Exemple

>>> assert not conflit(diff1, diff2)
>>> print(applique(applique(texte, diff1), fusionne(diff1, diff2)))
['l', 'e', ', 'c', 'h', 'i', 'e', 'n', ', 'a', ', 't', 'r', 'è', 's', ',
    's', 'o', 'i', 'f']

Partie III : Calcul de différentiels par calcul de plus courts chemins

Dans cette partie on souhaite exprimer le problème de calcul de distance d'édition comme un problème de calcul de plus court chemin dans un graphe orienté pondéré. Pour deux textes texte

et texte

, on considère une grille de dimension

texte

dont chaque cellule est un sommet du graphe. On appelle sommet un couple

tel que

texte

. Chaque sommet

aura au plus trois arcs sortants vers des sommets parmi

. On appelle entrée du graphe le sommet

et sortie le sommet (len(texte

), len(texte

La Figure 4 présente la matrice de distance d'édition pour texte

['b', 'i', 'e', 'n'] et texte

, ainsi que le graphe associé, sans les poids des arcs.

Le graphe ne sera jamais explicitement représenté, mais nous sommes en mesure de calculer l'ensemble des arcs sortants de chaque sommet.

Question 14. Écrire une fonction successeurs(texte1, texte2, sommet) qui renvoie une liste de couples (voisin, distance), de taille au plus 3 , représentant les sommets destinations des arcs sortant du sommet sommet, avec les poids associés.
L'existence et la pondération des arcs devra permettre d'assurer la correspondance suivante entre le graphe et la matrice de distance d'édition de texte

et texte

: pour tout sommet

du graphe,

coïncide avec la longueur d'un plus court chemin de ( 0,0 ) à (

). Démontrer cette propriété avec une récurrence.

b	0	1	2	3	4	5
i	1	0	1	2	3	4
e	2	1	2	3	4	5
n	3	2	3	4	5	4
	4	3	4	3	4	5

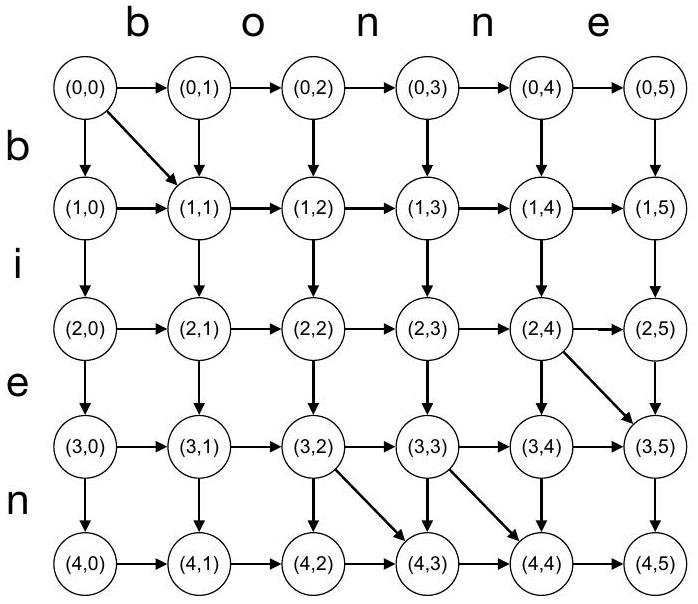
Figure 4 - Exemple de matrice de distance d'édition et de graphe associé (les poids des arcs ont été volontairement omis).

Exemple (les poids des arcs sont ici remplacés par ...)

>>> texte1 = ['b', 'i', 'e', 'n']
>>> texte2 = ['b', 'o', 'n', 'n', 'e']
>>> successeurs(texte1, texte2, (2,4))
[((3, 4), ...), ((2, 5), ...), ((3, 5), ...)]

Pour calculer un plus court chemin, on peut utiliser une variante l'algorithme de Dijkstra, présentée dans la Figure 5. Il s'appuie sur une structure de données de file de priorité sur les sommets

du graphe, dont on ne précise pas l'implémentation mais dont on précise ici la complexité des différentes opérations élémentaires.

La fonction vide() construit une file vide (de cardinal 0) en .
La fonction est_vide(file) teste si la file file est vide en .
La fonction extraire_min(file) supprime l'élément de priorité minimale dans la file file et le renvoie. En cas d'égalité de priorités, elle renvoie le sommet le plus petit pour l'ordre lexicographique parmi les sommets de priorité minimale. Sa complexité est en cardinal(file))).
La fonction ajoute(file, sommet, priorité) ajoute à la file file un sommet sommet avec une priorité priorité. L'opération augmente de 1 le cardinal de la file si le sommet n'est pas déjà présent avec cette priorité. Sa complexité est en .

def dijkstra(texte1, texte2):
    entrée = (0, 0)
    sortie = (len(texte1), len(texte2))
    file = vide()
    dist = {}
    vue = {}
    horloge = 0
    ajoute(file, entrée, 0)
    dist[entrée] = 0
    while not est_vide(file):
        sommet = extraire_min(file)
        if not sommet in vue:
            vue[sommet] = horloge
            horloge +=1
            if sommet == sortie:
                dist_final = {sommet: dist[sommet] for sommet in vue}
                return dist_final
            for voisin, distance in successeurs(texte1, texte2, sommet):
                d = dist[sommet] + distance
                if not voisin in dist or d < dist[voisin]:
                    dist[voisin] = d
                    ajoute(file, voisin, d)
    assert False

Figure 5 - Une variante de l'algorithme de Dijkstra.

Question 15. En vous appuyant sur les propriétés de l'algorithme de Dijkstra vues en cours, expliquer pourquoi l'utilisation de la fonction dijkstra permet de calculer la distance d'édition entre texte

et texte

. Préciser ce que contient le dictionnaire dist_final renvoyé, en caractérisant soigneusement l'ensemble des clés de ce dictionnaire.

Question 16. Donner la complexité de la fonction dijkstra et commenter son intérêt par rapport à l'algorithme de programmation dynamique de la partie II.

On s'intéresse maintenant à l'algorithme

, présenté dans la Figure 6. Il s'appuie sur une fonction heuristique h qui estime la distance de chaque sommet à la sortie du graphe. On admet que cet algorithme renvoie un dictionnaire dist_final tel que dist_final [sortie] est la longueur d'un plus court chemin de l'entrée à la sortie du graphe, si la fonction heuristique h utilisée est admissible, c'est à dire si pour tout sommet s du graphe, h (texte

, texte

) est inférieure ou égale à la longueur pondérée d'un plus court chemin de s jusqu'à la sortie du graphe.

Question 17. Donner une fonction

qui satisfait cette hypothèse, avec une complexité en

, et qui permet un gain de temps de calcul (vis-à-vis du nombre de sommets extraits de la file avant de rencontrer la sortie) sur l'exemple texte

, texte

. Justifier en comparant les dictionnaires dist_final renvoyés par les deux algorithmes sur cet exemple.

def astar(texte1, texte2):
    entrée = (0, 0)
    sortie = (len(texte1), len(texte2))
    file = vide()
    dist = {}
    vue = {}
    horloge = 0
    ajoute(file, entrée, 0)
    dist[entrée] = 0
    while not est_vide(file):
        sommet = extraire_min(file)
        vue[sommet] = horloge
        horloge += 1
        if sommet == sortie:
            dist_final = {sommet: dist[sommet] for sommet in vue}
            return dist_final
        for voisin, distance in successeurs(texte1, texte2, sommet):
            d = dist[sommet] + distance
            if not voisin in dist or d < dist[voisin]:
                dist[voisin] = d
                ajoute(file, voisin, d + h(texte1, texte2, voisin))
    assert False

Figure 6 - Algorithme

1. On rappelle qu'une structure immuable est une structure qui n'est jamais modifiée. C'est par exemple le cas des chaînes et des tuples en Python.
1. Une pile est ici implémentée par une liste Python.
1. Cette distance est communément appelée distance de Levenshtein.
2. Dans ce sujet, nous représenterons ces matrices par des listes de listes d'entiers.
1. On rappelle que l'ordre lexicographique sur les paires est défini par ( ) si et seulement si ou ( et ).

F	U		A	B	C	C	Y		Z
	0	1	2	3	4	5	6	7	8
	1	2	1	2	3	4	5	6	7
	2	3	2	1	2	3	4	5	6
	3	4	3	2	1	2	3	4	5
	4	5	4	3	2	3	4	5	6
	5	6	5	4	3	2	3	4	5
	6	7	6	5	4	3	4	5	6
	7	8	7	6	5	4	5	6	7

F	U		A	B	C	C	Y		Z
	0	1	2	3	4	5	6	7	8
	1	2	1	2	3	4	5	6	7
	2	3	2	1	2	3	4	5	6
	3	4	3	2	1	2	3	4	5
	4	5	4	3	2	3	4	5	6
	5	6	5	4	3	2	3	4	5
	6	7	6	5	4	3	4	5	6
	7	8	7	6	5	4	5	6	7

F	U		A	B	C	C	Y		Z
	0	1	2	3	4	5	6	7	8
	1	2	1	2	3	4	5	6	7
	2	3	2	1	2	3	4	5	6
	3	4	3	2	1	2	3	4	5
	4	5	4	3	2	3	4	5	6
	5	6	5	4	3	2	3	4	5
	6	7	6	5	4	3	4	5	6
	7	8	7	6	5	4	5	6	7