Pour les épreuves d'admissibilité, l'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé, une seule à la fois étant admise sur la table ou le poste de travail, et aucun échange n'est autorisé entre les candidats.

Ecoulements compressibles : modèle 1 D.

Fig. 1 - Tube de Pitot au nez de "Concorde" (protégé par un cache et sa flamme).

Les parties 2 et 3 sont largement indépendantes.

Introduction

Le but de ce problème est de rendre compte des principales propriétés d"un écoulement de gaz pour un spectre de vitesse s'étendant de

jusqu'à

ou 6 , où M est le nombre de Mach de l'écoulement, c'est-à-dire le rapport de la vitesse de l'écoulement à la vitesse du son, au point considéré.

Ces écoulements sont d'une grande importance puisque rencontrés dans tous les domaines de l'aérodynamique ainsi qu’au sein des machines thermiques comme les moteurs de fusée, les chambres de combustion des réacteurs d"avion ou les moteurs à combustion interne.

Dans tout le problème, le gaz considéré est l'air de l'atmosphère, que I'on considère comme une substance pure, constituée d'un seul type de molécules.

D"autre part, on rappelle qu'une particule fluide (échelle mésoscopique) contient un nombre suffisant de molécules pour que les grandeurs thermodynamiques issues de moyennes statistiques comme la pression,

, la température

, la masse volumique

y aient un sens, mais que ce nombre de molécules reste infinitésimal à l'échelle macroscopique.

Néanmoins; pour qu’en chaque point de l’écoulement on puisse effectivement parler de température, de pression ou de n'importe quelle grandeur thermodynamique, il est nécessaire de supposer l'existence d'un équilibre thermodynamique local.

Cela revient à considérer que le temps caractéristique d'établissement de l'équilibre thermodynamique au sein d'une particule fluide est très inférieur au temps caractéristique de variation de l'écoulement correspondant. Cette hypothèse, bien vérifiée expérimentalement ; permet de considérer que du point de vue thermodynamique, l'évolution temporelle d'une particule fluide est une suite d'états d'équilibre où les grandeurs thermodynamiques sont à chaque instant parfaitement définies.

Formulaire

Constante des gaz parfaits : ;
Masse molaire de l'air ;
Constante massique de l'air ;

Ecoulements compressibles : modèle 1 D.

Pour l'air : ;
Atmosphère standard (std) au voisinage du sol :
,
,
1 nœud=1 kt (de l'anglais knot) est l'unité de vitesse internationale en aéronautique.
mille marin à l'heure, soit .

Questions préliminaires

0.1 Expliquer succinctement mais précisément la différence entre la description lagrangienne et la description eulérienne d'un fluide.
0.2 On modélise l'écoulement en supposant qu'il est stationnaire et que toutes les grandeurs rencontrées ne dépendent que d'une dimension

de l'espace; toutes les dérivées par rapport à

sont nulles :

On néglige aussi la viscosité du gaz en se plaçant en dehors de la couche limite liée aux parois. La vitesse d'une particule fluide s'écrit donc

et toutes les grandeurs thermodynamiques ne sont fonction que de la variable x : pression

, température

, masse volumique

.
Que devient dans ce cadre l'expression de la dérivée particulaire

1 Grandeurs thermodynamiques:

Dans toute la suite du problème, on considère les grandeurs spécifiques, i.e. ramenées à l'unité de masse du système, attachées au fluide.

, h et s sont respectivement l'énergie interne spécifique, l'enthalpie spécifique et l'entropie spécifique au sein du gaz, alors l'énergie interne, l'enthalpie et l'entropie d'une particule fluide de masse dm sont respectivement u.dm, h.dm et s.dm.

D'autre part, en l'absence de turbulence, les particules fluides ne se mélangent pas les unes aux autres par convection.

La seule cause d'échange d'énergie calorifique entre particules reste la diffusion thermique dont les échelles de temps

sont très supérieures au temps caractéristique de l'écoulement

. Par conséquent, l'écoulement est adiabatique ; les particules fluides n'échangent pas de chaleur avec le reste du fluide.

1.1 Entropie:

Que dire de l'entropie spécifique d'une particule fluide en l'absence de discontinuité des variables internes?

1.2 Énergie interne:

Ecoulements compressibles : modèle 1 D.

Soit u, l'énergie interne spécifique de l'écoulement. Dans toute la suite, on considère que seules les forces de pression travaillent. Montrer que

varie entre x et

selon :

On notera si besoin est

la variation du volume dV d'une particule fluide de masse dm .

1.3 Enthalpie:

On rappelle que pour un système thermodynamique quelconque, l'enthalpie est définie par

. Montrer que pour l'enthalpie spécifique

, on a :

1.4 Écoulement stationnaire unidimensionnel (1 D) : conservation de l'énergie:

Montrer par un bilan clair et détaillé sur un système que l'on précisera, que la conservation de l'énergie s’écrit :

1.5 Gaz parfait

1.5.1 L'air se comportant comme un gaz parfait, montrer que l'équation d'état s'écrit :

Que pouvez vous dire de

et de h

-priori?
On suppose de plus que les chaleurs massiques à volume constant

et à pression constante

sont des constantes sur la plage de température envisagée. On pose

.
Exprimer

en fonction de

et de constantes

1.5.2 Relation de Saint-Venant:

Établir, pour un écoulement stationnaire 1 D d'un gaz parfait, la relation suivante (dite de Saint- Venant)

Quelle est la relation analogue à la relation de Saint- Venant (comportant aussi un terme en

) dans le cas où l'écoulement est incompressible? Comment s'appelle cette relation?

Ecoulements compressibles : modèle 1 D.

1.5.3 Vitesse du son et nombre de Mach:

La propagation du son dans un milieu élastique correspond à la propagation d'une perturbation de faible amplitude.

Donner l'ordre de grandeur de la surpression correspondant à un son modérément intense dans l'air, sous une pression d'environ 1 atm.
La vitesse du son a se calcule à partir de la dérivée de la pression par la masse volumique :

Indiquer soigneusement la démarche et les équations conduisant à ce résultat, sans détailler les calculs associés.
3. Calculer a en fonction de

et T .

2 Écoulement 1D : application au tube de PitotDans toute cette partie, on suppose qu'il n'y a aucune discontinuité dans les grandeurs intensives rencontrées.

On considère le dispositif suivant, appelé tube de Pitot, dont le rôle est d'alimenter un ou plusieurs instruments embarqués, (badin, machmètre), et ainsi de fournir à l'équipage une indication de vitesse de l'aéronef relativement à la masse d'air, appelée vitesse indiquée et notée

Le tube de Pitot permet de capter physiquement deux informations qui sont la pression totale

et la pression statique

La pression totale est la pression de recompression qui se manifeste au point d'arrêt de l'écoulement, à l'avant du tube. La pression statique est la pression captée par les orifices situés sur le côté du tube, tangentiellement à l'écoulement. La pression statique est la pression qu'un baromètre au repos relativement au fluide indiquerait : on admet que la pression statique est identique à la pression atmosphérique qui règne à l'endroit où se trouve l'aéronef :

On note

la pression et la température dans l'air non perturbé, en amont de l'aéronef, à la même altitude.

On s'intéresse à l'indication instrumentale

que le badin fournit à l'équipage.
Cet anémomètre embarqué est conçu de telle manière que, par un système de réservoirs placés en aval du tube de Pitot, l'instrument fait la différence entre

et donne en fin de compte une indication du type

Il s'agit donc de déterminer les relations existant entre la vitesse

, de l'écoulement et la différence de pression

On distingue les deux cas suivants :

2.1 Écoulement incompressible:

On suppose que pour l'écoulement considéré, l'air est incompressible

cte.

Ecoulements compressibles : modèle 1 D.

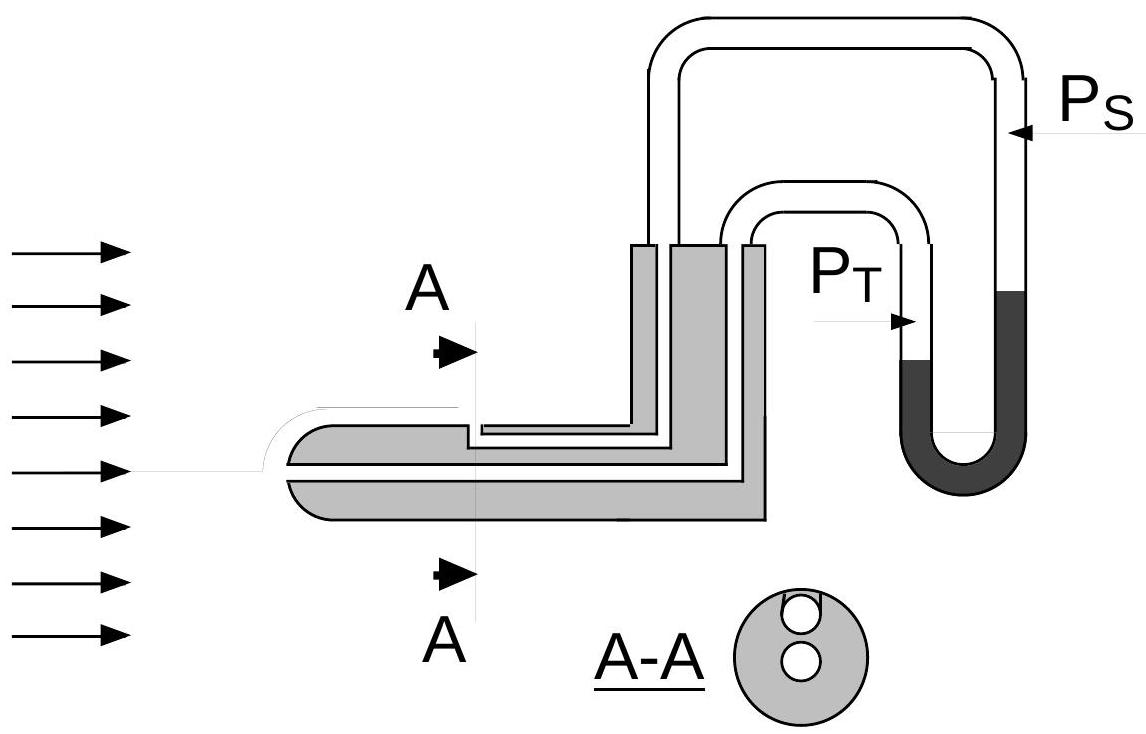
Fig. 2 - Schéma de principe du tube de Pitot

2.1.1 Calculer alors la vitesse V de l'écoulement en fonction de

, et

.
2.1.2 Dans les appareils anciens ou peu rapides (ce que l'on précisera dans la question suivante), l'instrument est étalonné en fonction de cette loi d'écoulement incompressible pour

correspondant aux conditions dites "standard" ( cf formulaire). Dans ce cas, on dit que l'instrument est gradué en équivalentvitesse EV.

Comparer l'équivalent-vitesse EV avec la vitesse réelle V de l'écoulement.
Que se passe-t-il en altitude, où la pression

est plus faible que

(à la même température) ?
2.2 Écoulement compressible On note M le nombre de Mach de l'écoulement :

On remarque que le nombre de Mach est un nombre local, puisqu'il dépend de la température de l'air au point considéré :

donc

.
2.2.1 Exprimer

en fonction de

et de M , puis déterminer la vitesse V de l'écoulement en fonction de

et de la vitesse du son a.

Comme seule la différence de pression

est accessible, les anémomètres de bord (badins) sont étalonnés en faisant correspondre à

une vitesse conventionnelle

donnée par :

où

est la vitesse du son dans les conditions standard.

Ecoulements compressibles : modèle 1 D.

Si la pression est plus faible que la pression standard (avec la même température) que dire de

relativement à

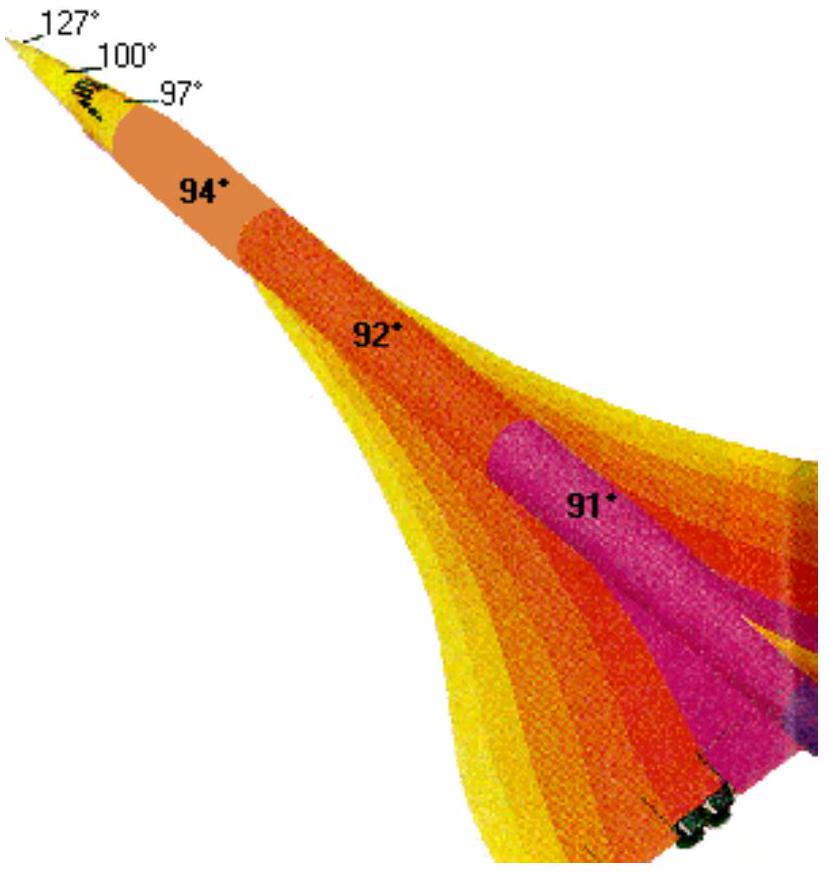
Fig. 3 - Courbes de niveau de températures sur le Concorde en vol (

2.2.2 On se place maintenant dans les conditions standard.

Dans les appareils modernes, l'équipage peut sélectionner une vitesse de vol indiquée que le Pilote Automatique (PA) maintient affichée sur l'indicateur de vitesse au nœud près (cf formulaire). Le but des questions suivantes est de déterminer la vitesse maximale

à partir de laquelle la différence

est supérieure à

, c'est-à-dire la vitesse à partir de laquelle la différence d'étalonnage des instruments entre l'échelle "équivalent-vitesse" et l'échelle "vitesse conventionnelle" devient sensible.

Exprimer en fonction de grâce à un développement limité au premier ordre non nul en M (on supposera ).
Calculer le nombre Mach maximal correspondant à en fonction de et .
Applications numériques : calculer puis en et en nœuds.

2.2.3 Échauffement de la cellule de "Concorde" en vol:

Calculer l'échauffement cinétique au nez de "Concorde" lorsque celui-ci vole en croisière à l'altitude de 15000 m à Mach 2,02 dans la stratosphère (entre

) où la température est constante et vaut

Comparer le résultat avec la figure 3 ci-dessus.

Ecoulements compressibles : modèle 1 D.

3 Écoulement 1D dans une tuyère dite de LavalOn considère maintenant un écoulement 1D à travers une tuyère représentée ci-dessous ( buse de Laval), constituée par un convergent, un col puis un divergent, dans le sens de l'écoulement.

Fig. 4 - Schéma de la buse de Laval.

Dans le réservoir d'air en amont règne la pression

, la température

, la masse volumique est

et la vitesse de l'écoulement est considérée comme nulle.

En modifiant la pression de sortie

, on aspire de l'air à travers la tuyère, ce qui crée un écoulement que l'on modélise comme un écoulement 1D.

On ne s'intéresse qu'aux régimes permanents, c'est-à-dire à des écoulements où les paramètres d'entrée et de sortie sont fixés depuis suffisamment longtemps pour que les régimes transitoires précédant l'établissement d'un régime stationnaire soient éteints.
3.1 Solutions de la tuyère 1D en fonction du nombre de Mach MÉtablir les relations suivantes :

Tracer

en fonction de M .

3.2 Fonctionnement de la tuyère : relations section-vitesse:

3.2.1 On note

la surface droite de la tuyère à l'abscisse x ( cl figure 4), que l'on note en abrégé S .

A partir de la conservation de la masse, établir une relation différentielle entre

, S et v .

Ecoulements compressibles : modèle 1 D.
3.2.2 Cas incompressible Que devient cette relation dans le cas où l'écoulement est incompressible ?

En déduire une évolution de la vitesse v de l'écoulement en fonction de l'évolution de la section S .

3.2.3 Cas compressible:

Établir une relation entre et .
Démontrer alors la relation suivante (théorème d'Hugoniot) :

3.2.4 : Comparer les cas compressible et incompressible.

Expliquer qualitativement la différence de comportement de l'écoulement entre ces deux situations.
3.2.5 On revient au cas compressible. Montrer que

n'est possible qu'à un seul endroit de l'écoulement, endroit que l’on précisera.
3.2.6 On note

, respectivement la pression, la température et la masse volumique au col lorsque l'écoulement est au moins sonique (i.e. lorsqu'il existe au moins un endroit où

).
Calculer

en fonction de

, puis faire l'application numérique.

3.3 Fonctionnement de la tuyère : débit massique:

3.3.1 Exprimer le débit massique

de la tuyère en fonction de

, S et v .

Soit le rapport

. Quelle est la dimension de

? Donner une interprétation physique de

.
3.3.2 Exprimer

en fonction de M et

.
3.3.3 Étudier les variations et tracer

en fonction de

.
3.3.4 Application numérique : calculer le débit volumique maximal par unité de surface

en fonction de

. On se place dans les conditions standard dans le réservoir en amont de la tuyère; calculer

3.4 Fonctionnement de la tuyère : analyse des solutions:

L'écoulement dans la buse est déterminé en fonction de la pression de sortie

réglée entre

(où l'écoulement n'existe pas) et des valeurs inférieures à

Ecoulements compressibles : modèle 1 D.

3.4.1 Fonctionnement adapté:

On appelle fonctionnement adapté de la tuyère l'ensemble des écoulements pour lesquels les solutions établies précédemment existent.

Montrer qu'en régime subsonique le fonctionnement de la tuyère est toujours adapté.

On note

la section de sortie de la tuyère et

la section au col. Dans le cas où

, indiquer par une méthode graphique, en traçant deux courbes sur un même schéma, comment déterminer le nombre de Mach de sortie

en fonction du nombre de Mach au col

.
2. Établir que si le débit est maximal, il existe deux solutions adaptées.

Toujours en supposant que

, déterminer graphiquement les nombres de Mach de sortie

dans ce cas.

Application numérique : calculer

ainsi que les pressions de sorties

correspondantes. On donne

les solutions réelles de l'équation

.
3.4.2 : On peut imposer une pression de sortie

quelconque entre 0 et

Parmi les équations caractérisant l'écoulement dans la tuyère, lesquelles ont une validité universelle?
Que pouvez-vous dire de l'écoulement lorsque

diminue progressivement à partir de

?
Quelle hypothèse précédemment faite doit-on abandonner pour obtenir une solution?
3.4.3 Tracer le débit massique

en fonction de la pression de sortie réduite

3.5 Fonctionnement de la tuyère : ondes de choc:

Lorsque la pression de sortie devient inférieure à la pression

, il apparaît à un endroit de l'écoulement situé après le col de la tuyère une onde de choc, c'est-à-dire une région de l'espace d'épaisseur

où certaines grandeurs physiques caractéristiques de l'écoulement varient de façon importante.

A l'échelle macroscopique, ces grandeurs apparaissent discontinues à la traversée de l'onde de choc.
Cette partie s'attache à déterminer certaines caractéristiques des ondes de choc ainsi que les principales relations de passage (ou relations de saut) des grandeurs physiques avant et après l'onde de choc.

L'expérience montre que dans le divergent de la tuyère, l'onde de choc est droite, ce qui signifie que la zone de discontinuité est un segment droit perpendiculaire à l'écoulement. On s'intéresse à ce type d'onde de choc.

Question liminaire : que pensez-vous, à la lumière de l'analyse faite jusqu'ici, de l'évolution de la pression à travers une telle onde de choc?

Ecoulements compressibles : modèle 1 D.
3.5.1 Montrer, dans le cadre de ce modèle rigoureusement 1D, que la conservation de la quantité de mouvement s'exprime comme :

3.5.2 On note

d'une part et

d'autre part, les vitesses, masses volumiques, pressions et températures respectivement avant et après l'onde de choc (cf figure 5).

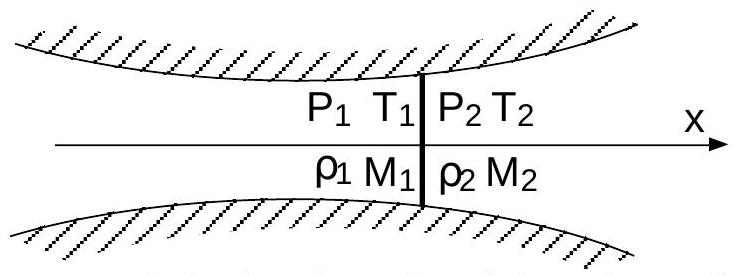
Fig. 5 - Onde de choc droite dans la buse de Laval

Écrire des relations entre ces grandeurs en utilisant trois équations de conservation (masse, quantité de mouvement et énergie).
3.5.3 Température totale On note

la température dite totale en un point de l'écoulement.

Montrer que la température totale est continue à la traversée de l'onde de choc.

3.5.4 Nombre de Mach

On note la vitesse critique du son, i.e la vitesse du son à l'endroit de l'écoulement où soit . Montrer que la vitesse critique est la même en amont et en aval de l'onde de choc.
A partir des équations de conservation, on établit la relation de Prandtl , que l'on admettra.
Soit le nombre de Mach juste avant l'onde de choc et juste après.

Exprimer le produit

en fonction de

.
3. En déduire

en fonction de

avec une condition sur

.
3.5.5 Pression et masse volumique totales Les grandeurs totales

(Pression totale) et

(masse volumique totale) sont définies isentropiquement à partir des grandeurs statiques correspondantes (à l'instar de la température totale

) : ce sont les grandeurs que l'on obtiendrait en un point d'arrêt situé sur une ligne de courant isentropique (en l'absence d'onde de choc,

est la pression qui règne au niveau de la prise de pression totale d'un tube de Pitot).

Exprimer en fonction de et .

Ecoulements compressibles : modèle 1 D.
2. Calculer

en fonction de

. En déduire

en fonction des mêmes variables, puis montrer que

.
3. Établir alors le résultat suivant :

3.5.6 Entropie Soit

la variation d'entropie spécifique de l'écoulement entre l'amont et l'aval de l'onde de choc.

Écrire, pour une particule fluide, la variation ds d'entropie spécifique en fonction de , du et . Que vaut ds en l'absence d'onde de choc?
Exprimer en fonction de et .
Exprimer alors en fonction de et .

En déduire

en fonction de

.
4. Établir alors sur le Mach amont

une condition nécessaire à l'existence d'une onde de choc. Que dire alors du Mach aval

, ainsi que de la condition sur

trouvée en 3 ?

3.5.7 Ondes de choc droites : bilan

Calculer les relations de saut , puis , en fonction de et de . Comparer avec la question liminaire du 3.5 :
Quelles sont les limites de , de , de et de , lorsque et lorsque . Tracer sommairement un graphe de ces grandeurs en fonction de .

4 Écoulement supersonique autour d'un appareilOn transpose l'analyse faite pour le modèle de la tuyère 1D à l'écoulement de l'air autour d'un appareil en vol.
4.1 Pourquoi cette transposition donne d'excellents résultats, en particulier en ce qui concerne l'écoulement autour des ailes?

Lorsque le Mach global - 1.e le nombre de Mach lié au centre de gravité de l'appareil est inférieur à 1, pensez-vous qu'il puisse apparaître des ondes de choc liées à l'écoulement de l'air autour de l'appareil?
4.2 Lorsque le Mach global est supérieur à 1, on parle de régime supersonique franc.

En régime supersonique franc, une onde de choc se forme en amont de l'appareil et (au moins) une autre en aval (cl figure 6 ci-dessous).

En général, cette onde de choc n'est pas droite, mais oblique, et d'autant plus inclinée que le Mach global est grand. Néanmoins, on supposera qu'à l'avant d'un tube de Pitot installé sur l'appareil, l'écoulement ne traverse qu'une seule onde de choc supposée droite.(cl figure 7 ci-dessus).

Ecoulements compressibles : modèle 1 D.

Fig. 6 - Ondes de choc autour d'un avion en vol supersonique

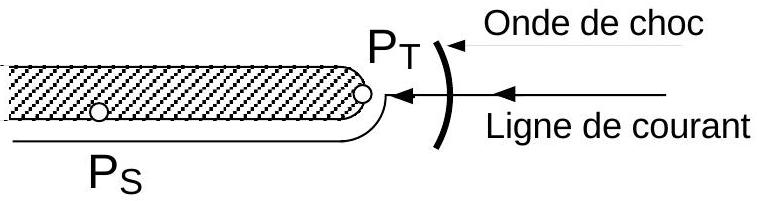
Fig. 7 - Onde de choc droite devant un tube de Pitot.

4.2.1 Retour sur l'échauffement cinétiquePourquoi la température calculée au 2.2.3: correspond si précisément à la température mesurée au nez du "Concorde" à Mach 2,02?

4.2.2 Retour sur le tube de Pitot :

Dans la situation de la figure 7, établir le rapport

en fonction de M et de

(formule dite de Rayleigh), où

est la pression totale prise au point d'arrêt du tube de Pitot et

est la pression statique captée par les orifices latéraux.

Cette formule montre que l'on peut mesurer la vitesse d'un appareil en vol supersonique en utilisant un indicateur de vitesse étalonné convenablement.

Par analogie avec la formule (7), établir la relation exprimant

en fonction de

permettant d'effectuer cet étalonnage.