Version interactive avec LaTeX compilé
MODÉLISATION EN SCIENCES PHYSIQUES ET SCIENCES DE L'INGÉNIEUR
Durée: 5 HEURES
Aucun document
Pour les épreuves d'admissibilité, l'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé, une seule à la fois étant admise sur la table ou le poste de travail, et aucun n'échange n'est autorisé entre les candidats.
Introduction
L'épreuve se décompose en deux problèmes, à traiter de préférence dans l'ordre proposé. Ils concernent tous deux la modélisation mathématique des phénomènes de combustion et d'explosion.
Le premier problème se focalise plus particulièrement sur les réactions explosives. Leurs principales caractéristiques ont été étudiées au milieu du XIXeme siècle par Van’t Hoff et Bunsen. Elles présentent la particularité d'avoir un taux de réaction qui dépend de manière non-linéaire et forte de la température (par opposition aux réactions lentes dont la dépendance est faible). Cette propriété de forte dépendance est due à une grande énergie d'activation de la réaction de combustion; elle se couple en général à une forte puissance thermique de la réaction. Dans ces conditions, un phénomène d'autocatalyse thermique peut se produire, provoquer l'emballement de la réaction et une très forte augmentation de la température; ce phénomène est appelé explosion thermique. Divers travaux expérimentaux ont alors conduit N.N. Semenov à développer la théorie de l'explosion thermique dans les années 1920 pour le cas d'un réacteur homogène. Frank-Kamenetskii a ensuite repris cette théorie dans le cas non-homogène et proposé un traitement exhaustif dans un certain nombre de cas.
Le but du problème I est d'introduire ces théories et de saisir les mécanismes de base de couplage entre le terme source thermique issu de la réaction chimique, la conduction thermique et les pertes thermiques au bord des domaines considérés. Le but est d'obtenir les conditions critiques d'explosion, i.e. les valeurs limites de certains paramètres qui déterminent si le phénomène d'explosion a lieu ou non. Finalement, le dernier point que nous aborderons sera le couplage entre l'explosion thermique et la convection naturelle en présence du champ de gravitation. Ces études sont importantes et trouvent de nombreuses applications dans la détermination des conditions de sécurité pour le stockage de matières dangereuses.
Dans le problème
Notation : Dans toute l'épreuve, on utilisera les notations suivantes pour les dérivées,
Note : Le premier problème requiert l'utilisation du théorème de Cauchy-Lipschitz. Il est rappelé dans l'énoncé.
Problème I
I Présentation
Nous allons dans un premier temps considérer les équations qui régissent l'écoulement d'un mélange gazeux réactif compressible dans un domaine bi-dimensionnel
Ce type d'écoulement est régi par un système d'équations aux dérivées partielles pour lequel le vecteur des variables est
où
La pression
où
par définition de
par définition de
Le système de base que nous venons d'évoquer est souvent utilisé dans l'approximation de Oberbeck-Boussinesq qui considère que la pression et la densité volumique de masse sont quasiment constantes
I. 1 On suppose que le mélange gazeux est initialement à la température
I. 2 Montrer, en utilisant cette loi d'état, que l'approximation de Oberbeck-Boussinesq est valable pour de faibles variations de température, c'est-à-dire
I. 1 On suppose que le mélange gazeux est initialement à la température
I. 2 Montrer, en utilisant cette loi d'état, que l'approximation de Oberbeck-Boussinesq est valable pour de faibles variations de température, c'est-à-dire
Avant de revenir sur les équations dans la dernière partie du problème, nous allons commencer par comprendre les mécanismes de base sur des modèles simplifiés.
II Explosion Adiabatique Homogène
Le but de cette partie est de faire apparaître, dans la cadre d'une modélisation minimale, l'échelle de temps du problème. On se place dans le cadre d'une chimie simple, c'est-à-dire, d'une chimie constituée d'une unique réaction globale irréversible "Fuel
strictement positives. On ne prend en compte, dans ce modèle, que le chauffage du milieu par la réaction et l'on suppose que le système est isolé thermiquement de l'extérieur; on parle alors d'explosion thermique adiabatique.
Note : On donne ici un théorème utile pour la suite sous la forme d'une adaptation du théorème d'existence et unicité de solution de Cauchy-Lipschitz. On considère un système d'équations différentielles ordinaires autonome:
avec
THÉORÈME : On considère un ensemble compact
THÉORÈME : On considère un ensemble compact
COROLLAIRE: Sous les hypothèses du théorème précédent, si deux solutions
L'idée sous-jacente est que sous des hypothèses de régularité de
II. 1 Le but de cette question est de montrer l'existence d'une solution pour tout temps et d'obtenir des renseignements sur la structure qualitative de la solution du système (II.1-II.2).
II.1.a Montrer que, du système (II.1-II.2), on peut déduire une équation sur une quantité
II.1.b En déduire une équation autonome sur la variable
L'idée sous-jacente est que sous des hypothèses de régularité de
II. 1 Le but de cette question est de montrer l'existence d'une solution pour tout temps et d'obtenir des renseignements sur la structure qualitative de la solution du système (II.1-II.2).
II.1.a Montrer que, du système (II.1-II.2), on peut déduire une équation sur une quantité
II.1.b En déduire une équation autonome sur la variable
et expliciter la fonction
II.1.c En appliquant le théorème donné ci-dessus, montrer qu'il existe une unique solution maximale
II.1.d Montrer que
II.1.e Déduire de II.1.c que la limite de
II.1.f Représenter graphiquement le comportement qualitatif de la solution.
II.1.g Proposer une équation différentielle autonome décrivant l'évolution de la température
II.1.c En appliquant le théorème donné ci-dessus, montrer qu'il existe une unique solution maximale
II.1.d Montrer que
II.1.e Déduire de II.1.c que la limite de
II.1.f Représenter graphiquement le comportement qualitatif de la solution.
II.1.g Proposer une équation différentielle autonome décrivant l'évolution de la température
La structure de la non-linéarité
[H1] La réaction satisfait l'hypothèse des grandes énergies d'activation si
[H1] La réaction satisfait l'hypothèse des grandes énergies d'activation si
où
II.1.g On se place dans le cas où
II. 2 Nous allons maintenant étudier un modèle approché pour le système (II.1-II.2).
II.2.a Adimensionner l'équation vérifiée par la température et écrire pour cela une équation sur la température réduite
II.2.b Montrer que, sous les hypothèses
II.1.g On se place dans le cas où
II. 2 Nous allons maintenant étudier un modèle approché pour le système (II.1-II.2).
II.2.a Adimensionner l'équation vérifiée par la température et écrire pour cela une équation sur la température réduite
II.2.b Montrer que, sous les hypothèses
avec la condition initiale
II.2.c Dans l'équation précédente, on a remplacé sous l'hypothèse [
II.2.d On pose
II.2.e Décrire le comportement "explosif" de cette solution. Tracer l'évolution temporelle de la solution
II.2.f On appelle
II. 3 Il s'agit de montrer que l'équation simplifiée (II.5) est un "bon modèle" et d'en déduire le comportement qualitatif général de la solution de (II.1-II.2).
II.3.a Montrer que la condition de validité
II.3.b Calculer la température correspondant au taux de réaction maximum, en valeur absolue, pour le système (II.1-II.2), sachant que le taux de réaction est le second membre de l'équation sur
II.3.c Quel scénario peut-on déduire sur l'évolution du système (II.1-II.2) dans la mesure où le taux de réaction maximum est atteint dans un proche voisinage de
II.3.d Caractériser l'évolution du système dans le plan des variables dimensionnées
II.3.e Que se passe-t-il pour la consommation de fuel (caractérisée par la fraction massique de fuel
II.3.f Que devient l'évolution du système quand l'énergie d'activation devient de plus en plus grande?
II.3.g On choisit une application numérique avec
II.2.c Dans l'équation précédente, on a remplacé sous l'hypothèse [
II.2.d On pose
II.2.e Décrire le comportement "explosif" de cette solution. Tracer l'évolution temporelle de la solution
II.2.f On appelle
II. 3 Il s'agit de montrer que l'équation simplifiée (II.5) est un "bon modèle" et d'en déduire le comportement qualitatif général de la solution de (II.1-II.2).
II.3.a Montrer que la condition de validité
II.3.b Calculer la température correspondant au taux de réaction maximum, en valeur absolue, pour le système (II.1-II.2), sachant que le taux de réaction est le second membre de l'équation sur
II.3.c Quel scénario peut-on déduire sur l'évolution du système (II.1-II.2) dans la mesure où le taux de réaction maximum est atteint dans un proche voisinage de
II.3.d Caractériser l'évolution du système dans le plan des variables dimensionnées
II.3.e Que se passe-t-il pour la consommation de fuel (caractérisée par la fraction massique de fuel
II.3.f Que devient l'évolution du système quand l'énergie d'activation devient de plus en plus grande?
II.3.g On choisit une application numérique avec
-
tel que , -
tel que le taux de réaction est à son maximum.
Commenter. (Remarque : les données numériques ne permettent pas de calculer
iii Traitement des Pertes Thermiques
Dans la partie précédente, l'absence de perte thermique au bord du réacteur engendre systématiquement l'explosion thermique car la température ne peut qu'augmenter et atteindre
Un modèle simple de perte, dans le cas d'un réacteur fermé, est de fixer la température à la paroi à la température de réference
où
III. 1 Nous nous intéressons brièvement au comportement qualitatif général des solutions du système pour
III.1.a Appliquer le théorème donné dans l'énoncé et montrer l'existence d'une solution maximale
III.1.b Montrer que
III.1.c Montrer que la quantité
III.1.d Montrer que
III.1.e Montrer, en utilisant le même type d'argument que dans la partie II, que
III.1.f Déduire des questions qui précèdent que
III.1.g Donner le comportement qualitatif du système. Tracer la forme de
III.1.h Adimensionner les équations (III.1-III.2) en utilisant le même adimensionnement que dans la partie II, et en prenant comme temps adimensionné
III. 2 Comme la quantité
III.2.a Montrer que, sous les hypothèses
III. 1 Nous nous intéressons brièvement au comportement qualitatif général des solutions du système pour
III.1.a Appliquer le théorème donné dans l'énoncé et montrer l'existence d'une solution maximale
III.1.b Montrer que
III.1.c Montrer que la quantité
III.1.d Montrer que
III.1.e Montrer, en utilisant le même type d'argument que dans la partie II, que
III.1.f Déduire des questions qui précèdent que
III.1.g Donner le comportement qualitatif du système. Tracer la forme de
III.1.h Adimensionner les équations (III.1-III.2) en utilisant le même adimensionnement que dans la partie II, et en prenant comme temps adimensionné
III. 2 Comme la quantité
III.2.a Montrer que, sous les hypothèses
où
III.2.b Sur quel intervalle de temps peut-on considérer que l'équation précédente est représentative de la physique du système (III.1-III.2) ? Quelle hypothèse implique son utilisation sur la consommation de fuel dans cet intervalle?
III.2.c Représenter sur un diagramme les graphes des deux fonctions
III.2.d Relier
III.2.e Classifier et caractériser les diverses dynamiques possibles pour l'équation (III.3) en fonction de rapport
III.2.f Que dire de la stabilité des points stationnaires quand ils existent (un point stationnaire est dit stable pour l'équation différentielle (III.3) si l'évolution d'une solution, dont la donnée initiale est prise dans un voisinage du point, est la convergence vers cet état stationnaire et instable dans le cas contraire) ?
III. 3 Parmi les divers scénarios proposés, certains correspondent au comportement du système (III.1-III.2) et d'autres non. Nous allons étudier ce point dans cette sous-partie.
III.3.a Montrer que cette correspondance est effective dans le cas
III.3.b Pour
III.3.c Dans le cas où il y a explosion pour l'équation (III.3), c'est-à-dire pour
III.2.b Sur quel intervalle de temps peut-on considérer que l'équation précédente est représentative de la physique du système (III.1-III.2) ? Quelle hypothèse implique son utilisation sur la consommation de fuel dans cet intervalle?
III.2.c Représenter sur un diagramme les graphes des deux fonctions
III.2.d Relier
III.2.e Classifier et caractériser les diverses dynamiques possibles pour l'équation (III.3) en fonction de rapport
III.2.f Que dire de la stabilité des points stationnaires quand ils existent (un point stationnaire est dit stable pour l'équation différentielle (III.3) si l'évolution d'une solution, dont la donnée initiale est prise dans un voisinage du point, est la convergence vers cet état stationnaire et instable dans le cas contraire) ?
III. 3 Parmi les divers scénarios proposés, certains correspondent au comportement du système (III.1-III.2) et d'autres non. Nous allons étudier ce point dans cette sous-partie.
III.3.a Montrer que cette correspondance est effective dans le cas
III.3.b Pour
III.3.c Dans le cas où il y a explosion pour l'équation (III.3), c'est-à-dire pour
Justifier la borne d'intégration en utilisant les hypothèses.
III.3.c On cherche la limite de ce temps quand
III.3.d Que conclure sur le modèle (III.3) au voisinage des conditions critiques en terme de l'hypothèse
III. 4 En fait, la restriction sur l'applicabilité du modèle quand on s'approche des conditions critiques n'a d'effet que dans un très petit voisinage inférieur de
III.4.a Présenter un diagramme des diverses évolutions temporelles possibles de la température dans le cas général du système (III.1-III.2).
III.4.b Donner l'évolution dans le plan de phase (
III.4.c Conclure cette étude.
III.3.c On cherche la limite de ce temps quand
III.3.d Que conclure sur le modèle (III.3) au voisinage des conditions critiques en terme de l'hypothèse
III. 4 En fait, la restriction sur l'applicabilité du modèle quand on s'approche des conditions critiques n'a d'effet que dans un très petit voisinage inférieur de
III.4.a Présenter un diagramme des diverses évolutions temporelles possibles de la température dans le cas général du système (III.1-III.2).
III.4.b Donner l'évolution dans le plan de phase (
III.4.c Conclure cette étude.
IV LE Cas Inhomogène : Diffusion
Nous allons maintenant considérer le cas inhomogène pour lequel les champs de température et fraction massique dépendent non seulement du temps, mais aussi de la variable d'espace. On se place dans le cadre particulier d'une bande infinie dans la direction horizontale
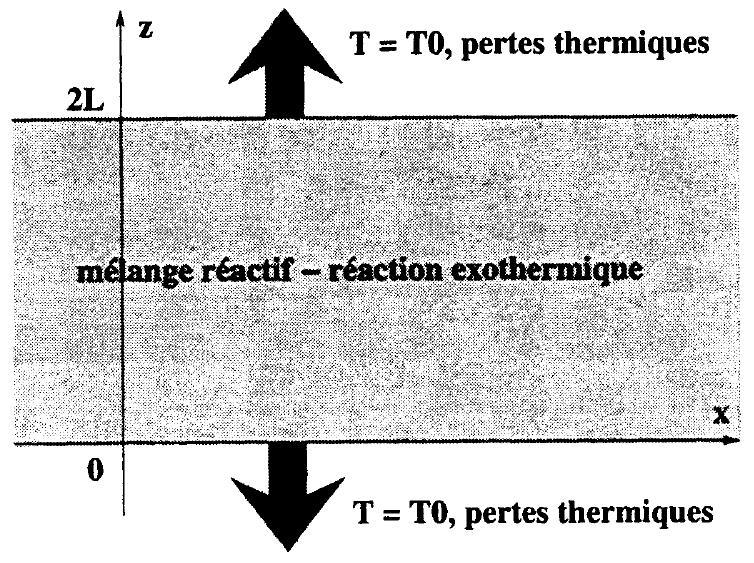
Figure 1 : Configuration
On considère alors le système de deux équations aux dérivées partielles suivant :
où
IV. 1
IV.1.a Ecrire une équation d'évolution sur la moyenne
IV.1.b En utilisant les conditions aux limites, le signe de
IV.1.c Faire le lien avec le modèle homogène de la partie III.
IV. 2 On introduit un temps de diffusion
IV.1.b En utilisant les conditions aux limites, le signe de
IV.1.c Faire le lien avec le modèle homogène de la partie III.
IV. 2 On introduit un temps de diffusion
où on explicitera et justifiera le calcul de
IV. 3 Donner une expression analytique implicite de l'état stationnaire
IV. 3 Donner une expression analytique implicite de l'état stationnaire
reliant
IV. 4 Tracer et donner la forme de cette fonction
IV. 5 Dans le cas
IV. 4 Tracer et donner la forme de cette fonction
IV. 5 Dans le cas
V Les Phénomènes Convectifs
Nous n'envisageons pas dans cette partie une étude complète des phénomènes de couplage entre l'explosion thermique dans une bande, comme dans le cas précédent, et la convection naturelle qui va se déclencher lorsque la température au centre dépasse un seuil de stabilité. Ce genre d'étude demande un ensemble de simulations numériques sur ordinateur et une investigation paramétrique. Dans ce contexte, le modèle à utiliser est un couplage entre une équation sur la température en variables adimensionnées :
où
V. 1 Expliquer, à la lumière des parties précédentes, pourquoi un modèle qui néglige la consommation du fuel, suppose de faibles variations de température et considère l'équation (V.1) permet de rendre compte d'une grande partie des phénomènes d'explosion pour un modèle plus complet quand les hypothèses
V. 1 Expliquer, à la lumière des parties précédentes, pourquoi un modèle qui néglige la consommation du fuel, suppose de faibles variations de température et considère l'équation (V.1) permet de rendre compte d'une grande partie des phénomènes d'explosion pour un modèle plus complet quand les hypothèses
Problème II
Dans ce second problème, nous allons aborder la théorie de la propagation de flammes planes laminaires. Ces objets monodimensionnel peuvent se voir, dans certains cas simples, comme des structures auto-similaires (c'est-à-dire dont le profil spatial est invariant au cours du temps) se propageant à vitesse
I Présentation
Nous allons aborder ces structures que l'on appelle "ondes progressives" pour des systèmes d'équations aux dérivées partielles, en dimension un d'espace, qui modélisent le couplage instationnaire entre des phénomènes de conduction thermique et des phénomènes de réaction chimique. Nous allons considérer une chimie simple du type "Fuel
pour
II Ondes Progressives
Nous allons donc chercher des profils
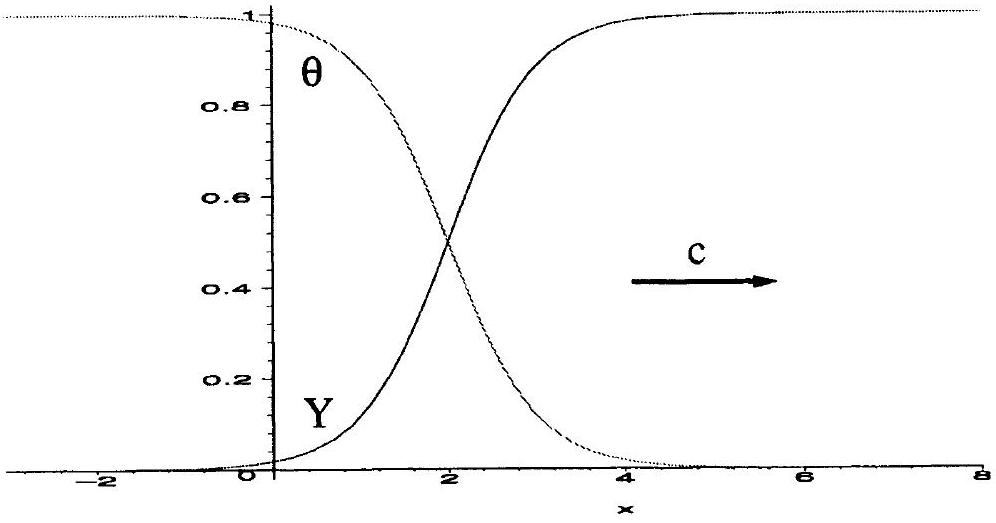
Figure 2 : Onde progressive
II. 1 De la même manière que dans le problème I, on peut se ramener à une seule équation sur la température; c'est l'objet de cette question.
II.1.a Dans un premier temps, on se donne une vitesse de flamme
II.1.b On note
II.1.c Montrer alors que le problème se réduit à une équation sur
II.1.a Dans un premier temps, on se donne une vitesse de flamme
II.1.b On note
II.1.c Montrer alors que le problème se réduit à une équation sur
et donner une expression explicite pour la non-linéarité
II. 2 On suppose que l'équation sur
II. 3 Nous allons maintenant faire quelques hypothèses sur la non-linéarité
II. 2 On suppose que l'équation sur
II. 3 Nous allons maintenant faire quelques hypothèses sur la non-linéarité
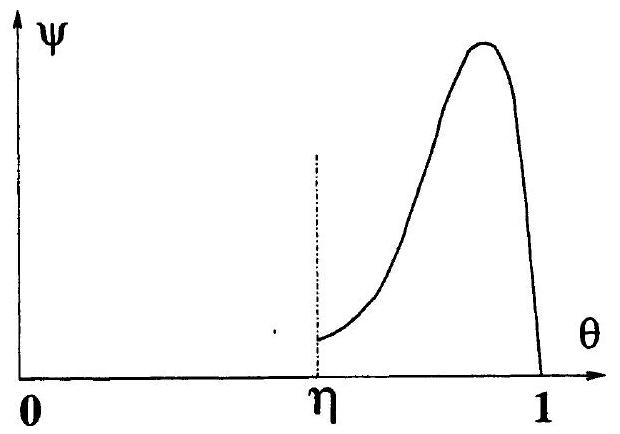
Figure 3 : Structure de la non-linéarité
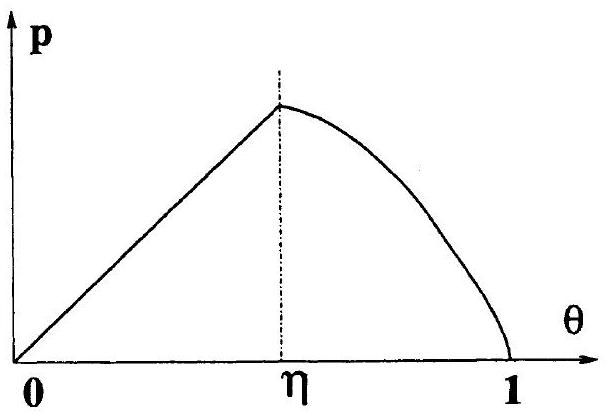
Figure 4 : Onde dans le plan de phase
On va réduire l'étude d'une équation du second ordre à celle d'un système de deux équations à deux inconnues du premier ordre et traiter l'existence dans le plan de phase
II.3.a On note
II.3.b Montrer que l'on peut reposer ce système dans le plan (
II.3.a On note
II.3.b Montrer que l'on peut reposer ce système dans le plan (
avec
II.3.c On cherche dans un premier temps
II.3.d On se place sur l'intervalle
II.3. e Résoudre l'équation dans l'intervalle
II.3.c On cherche dans un premier temps
II.3.d On se place sur l'intervalle
II.3. e Résoudre l'équation dans l'intervalle
III Vitesse et Limite
Nous allons maintenant donner une estimation sur la vitesse de flamme et en déduire sa limite dans le cas
III. 1 Dans cette question, on cherche à obtenir un encadrement de la vitesse de flamme en fonction de
III.1.a Montrer que
III.1.b En utilisant les mêmes arguments que dans la partie précédente et la fonction
III.1.c Pour obtenir une borne inférieure, utiliser la solution
III. 1 Dans cette question, on cherche à obtenir un encadrement de la vitesse de flamme en fonction de
III.1.a Montrer que
III.1.b En utilisant les mêmes arguments que dans la partie précédente et la fonction
III.1.c Pour obtenir une borne inférieure, utiliser la solution
sur l'intervalle
qui permet donc d'encadrer la vitesse de flamme en fonction du paramètre
III. 2 En supposant que
III. 2 En supposant que
