Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Système de rééducation musculaire par frein magnétique

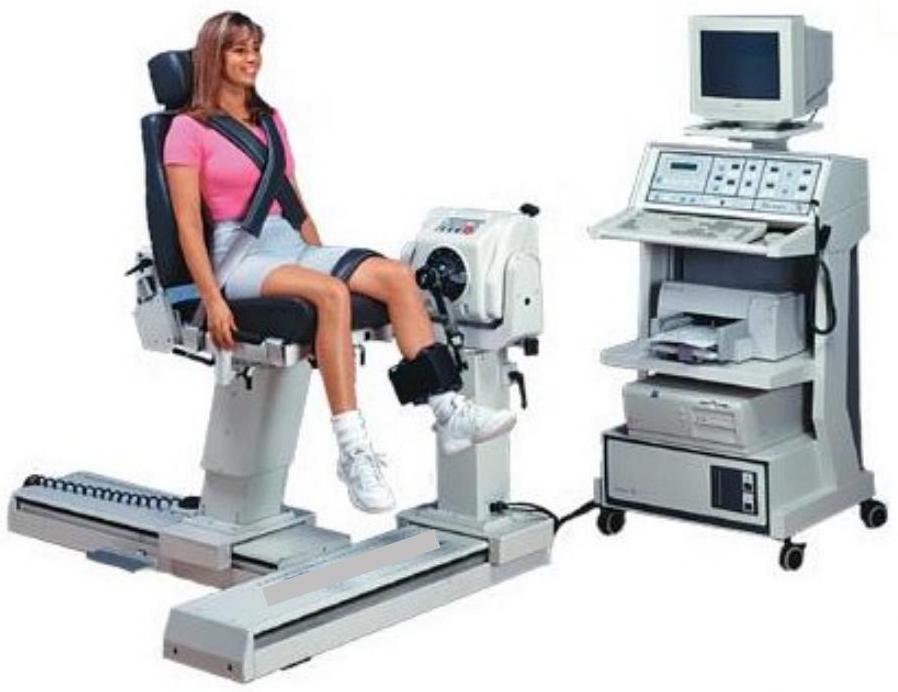
Figure 1 : exemple de système de rééducation musculaire par frein magnétique : la rééducation des muscles liés au genou.

Lorsqu'une personne se blesse gravement et qu'elle doit subir une opération chirurgicale, il est indispensable de lui redonner une excellente motricité une fois l'opération réalisée. Cela passe par de la rééducation musculaire, qui consiste à redonner aux muscles leur tonicité initiale. Dans la plupart des cas, cette rééducation se fait en utilisant des systèmes très simples, comme par exemple des haltères ou des pinces à ressorts. Cependant, lorsque les accidents sont graves, il est utile d'utiliser des machines aux fonctions complexes, comme celle représentée sur la figure 1.

Pour rééduquer les muscles d'une articulation, il est nécessaire de les faire travailler alternativement selon trois modes :

le mode isométrique : cela consiste à bloquer le mouvement articulaire du patient et à lui demander d'exercer avec son muscle l'effort maximum qu'il peut développer jusqu'à ce que la douleur devienne trop grande ;
le mode isocinématique : cela consiste à demander au patient de commander ses muscles pour bouger ses membres à vitesse constante ;
le mode isotonique : cela consiste à exercer sur les membres du patient un couple résistant constant, contre lequel les muscles doivent lutter au cours du mouvement qu'ils imposent.

La figure 2 montre une machine de rééducation classique, et son modèle mécanique associé. Le patient est assis sur un fauteuil. Il doit soulever des masses à l'aide de la partie inférieure de ses jambes, en agissant sur les muscles liés à son genou, en poussant sur un coussin d'appui. Cette machine est dite «passive», car elle ne contient aucun système de commande pour exercer des efforts résistants sur les muscles. Seule la gravité en exerce.

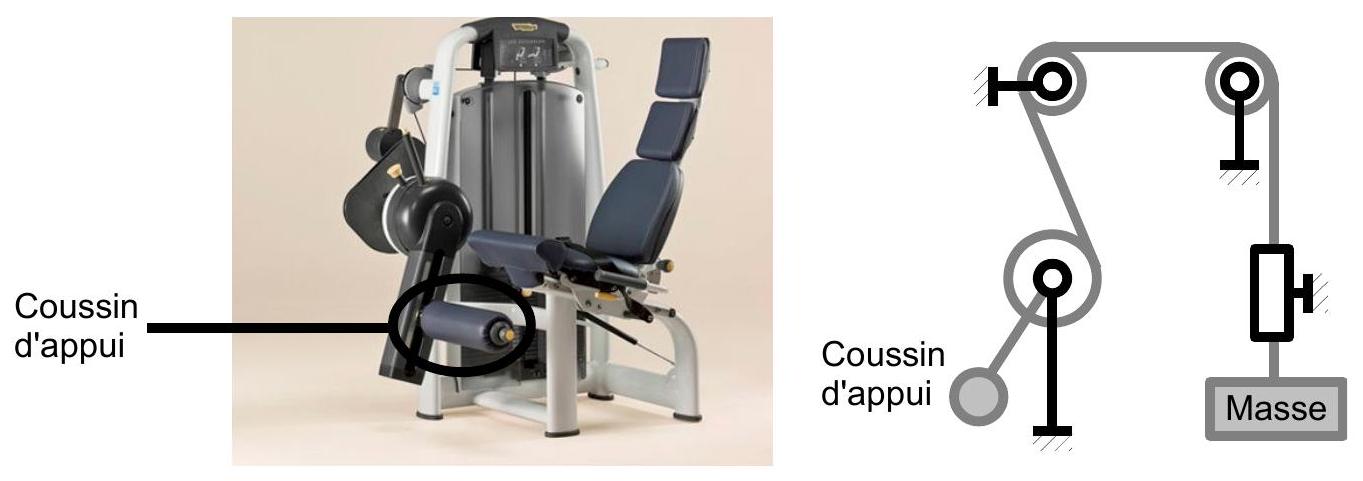
Figure 2 : machine de rééducation musculaire passive : photographie et modèle mécanique associé.

Q1: Indiquer quel(s) mode(s) de travail une machine passive, telle que celle représentée sur la figure 2, permet de réaliser.

Afin de permettre au patient de rééduquer ses muscles selon les trois modes, il est nécessaire de concevoir une machine dite «active», c'est-à-dire possédant un système de commande permettant de réguler les efforts résistants sur les muscles. Les performances attendues par une telle machine sont résumées dans le cahier des charges suivant.

Exigence	Niveau
Modes de fonctionnement	Isométrique, isocinématique et isotonique au choix
Stabilité	Mode isotonique	Marge de gain de la FTBO : 10 dB minimum Marge de phase de la FTBO :
Précision	Mode isométrique	de précision en position angulaire
	Mode isocinématique	Vitesse de rotation insensible aux perturbations en couple dues à l'homme
	Mode isocinématique	10% de précision en vitesse angulaire, en régime permanent
	Mode isotonique	Précision totale en couple

L'objectif de ce sujet est de concevoir une telle machine à partir d'un frein magnétique. L'épreuve est structurée ainsi : la partie 1 consiste à étudier un fluide particulier aux propriétés très adaptées à la problématique ; la partie 2 porte sur la conception d'un frein qui est alors intégré dans le système de rééducation, dont l'étude est menée dans la partie 3.

Même s'il est conseillé de traiter les parties dans l'ordre du sujet (pour comprendre la logique d'enchaînement des questions et les différentes notations), le candidat pourra, s'il le souhaite, tirer profit de l'indépendance des parties.

Partie 1 : étude du fluide magnéto-rhéologique

La rhéologie est une branche de la mécanique étudiant les déformations et l'écoulement de la matière sous l'effet d'une contrainte appliquée. Certaines catégories de fluides, découverts en 1949, possèdent la propriété de voir leur comportement rhéologique, principalement leur viscosité, modifié lorsqu'un champ magnétique ou électrique leur est appliqué. On les appelle fluides magnéto-rhéologique (MR) ou électrorhéologique (ER) et ce sont en général des huiles dotées de particules aux propriétés permettant de tels comportements. Dans le cas des fluides MR par exemple, la viscosité, faible en l'absence de champ magnétique, augmente lorsqu'on lui en applique un jusqu'à pouvoir se comporter quasiment comme un solide. L'utilisation d'électroaimants dans une chaîne asservie permet d'envisager de contrôler la «phase» du fluide et ainsi un grand nombre d'applications.

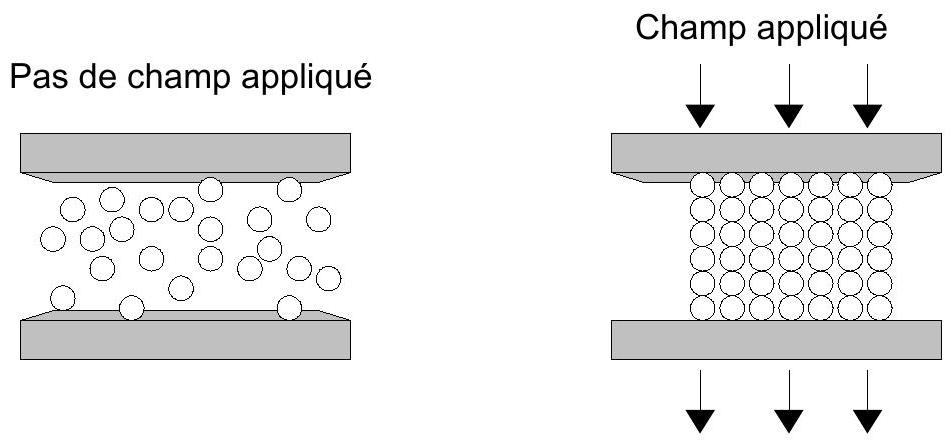
Figure 3 : principe de fonctionnement d'un fluide contrôlable.

En l'absence de champ, les particules sont dispersées de façon aléatoire dans le fluide. Lorsqu'un champ est appliqué, les particules se disposent selon des chaînes de direction colinéaire au champ (comme le montre la figure 3). Sur le dessin, on suppose que le déplacement du fluide s'effectue parallèlement aux plaques extérieures et que ces dernières sont fixes.

Q2 : À partir de la figure 3, expliquer physiquement pourquoi la viscosité du fluide augmente lorsqu'un champ règne dans le fluide. On parle sur cet exemple de mode valve ou clapet: expliquer. Dans le mode de cisaillement direct, seule une des plaques est fixe, la seconde se déplaçant de façon parallèle à la première sous l'action d'une force. Expliquer ce qu'il se passe et le terme de «cisaillement direct ».

À la différence des ferrofluides, autre catégorie de matériau intelligent, les fluides MR sont composés de particules plus grosses, de l'ordre du micromètre, là où les ferrofluides sont sensiblement des nanoparticules. Cela conduit à un comportement microscopique différent, puisque les ferrofluides peuvent rester en suspension sous l'effet du mouvement brownien alors que les fluides MR sont trop denses pour cela. De plus, aucun changement rhéologique n'apparaît lorsqu'un champ est appliqué à un ferrofluide. La figure 4 montre par exemple l'allure des particules magnétisables trouvées dans un fluide MR.

Q3 : Évaluer, à partir de la figure 4 et en supposant que celle-ci est typique d'un fluide MR, l'ordre de grandeur de la fraction (en pourcentage) du volume occupé par les
particules. Préciser également le volume typique d'une particule. Expliquer quelle grandeur risque de varier, et comment, si l'on modifie la densité des particules.

Figure 4 : particules magnétisables d'un fluide MR .

Fluides ER et MR: comparaison

Les développements technologiques récents sur les fluides MR permettent à ceux-ci de « rattraper» les performances des ER, alors qu'il étaient longtemps de qualités inférieures. Le tableau suivant résume les performances comparatives de ces deux types.

Fluide	ER	MR
Contrainte de rupture (kPa)	2 à 5	50 à 100
Viscosité (Pa.s)	0,1 à 10	0,1 à 10
Températures de fonctionnement en	- 25 à + 125	- 40 à + 150
Temps de réponse	Inférieur à 1 ms	Inférieur à 1 ms
Masse volumique (g. )	1 à 2	3 à 4
Type de champ d'excitation et valeur maximale	Électrique, ~ 4000000	Excitation magnétique, ~ 250000
Exigences électriques	2 à 5 kV pour 1 à 10 mA	2 à 25 V pour 1 à 2 A

Q4: Comparer les fluides MR aux ER. Comparer en particulier les plages de puissances électriques. Conclure sur le type de fluide le plus intéressant d'emploi.

Q5: Préciser pourquoi on considère l'excitation magnétique plutôt que le champ magnétique. Préciser les unités usuelles puis de base du Système International pour les deux champs maximaux.

Contrainte de cisaillement et équations du modèle

On se restreint dans tout le reste du sujet à un fluide MR . Le paramètre fondamental que contrôle l'intensité du champ magnétique est la contrainte de cisaillement du fluide notée

. En mécanique, la contrainte de cisaillement

est une contrainte appliquée tangentiellement (de manière parallèle) à la face d'un matériau, ce qui entraîne en général sa déformation. Plus particulièrement en mécanique des fluides, c'est cette contrainte qui permet d'expliquer les déplacements relatifs entre différentes
«couches» de fluide : en effet, la « couche» au contact des parois possède une vitesse nulle, la «couche» en contact avec la précédente «glisse» sur celle-ci un peu plus facilement, et ainsi de suite. Ce modèle permet de démontrer que les vitesses dans une conduite à symétrie cylindrique suivent un profil parabolique. À contrainte fixée, plus le fluide sera visqueux et plus les variations de vitesses dans le fluide seront faibles. On donne pour la suite la relation simplifiée entre la contrainte de cisaillement

, la viscosité

et le gradient de vitesse par rapport à la direction d'écoulement (par exemple selon

)

pour un type de fluide appelé fluide newtonien :

Dans une conduite, cette contrainte de cisaillement peut par exemple être créée par une différence de pression entre l'entrée et la sortie du tube. L'augmentation de cette contrainte est proportionnelle à celle du débit volumique

du fluide considéré.

Le père fondateur de la science rhéologique, Eugene Bingham, étudia au début des années 1920 l'écoulement des peintures, fluide non newtonien. La loi de Bingham est la première loi de comportement d'un «fluide à seuil», autrement dit un fluide ne se déformant qu'au-delà d'une certaine contrainte. Dans ce modèle théorique, il faut atteindre une certaine contrainte de cisaillement, appelée «contrainte d'écoulement»

pour que le débit commence à être non nul et varie par la suite proportionnellement à

avec le même coefficient de proportionnalité que celui du modèle newtonien.

Q6 : Tracer, à partir des indications du sujet et sans calculs, les allures des courbes donnant le débit d'une conduite donnée en fonction de la contrainte de cisaillement

, pour une fluide newtonien puis un fluide de Bingham. On indiquera en particulier la contrainte d'écoulement

Le débit dépendant de nombreux paramètres, principalement les données géométriques de la conduite, on préfère aujourd'hui utiliser le modèle plastique de Bingham donnant T en fonction de

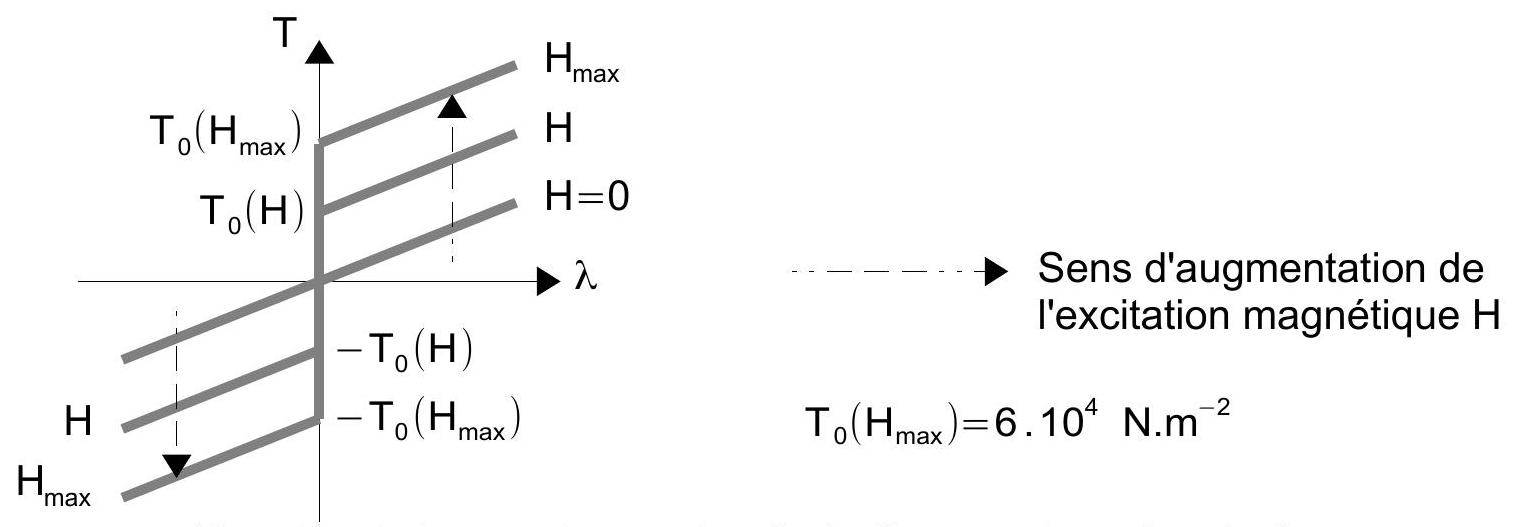
. Dans le cas d'un fluide MR , on peut même tracer les courbes en tenant compte de la contribution de l'excitation magnétique appliquée. On obtient ainsi une famille de courbes, comme sur la figure suivante :

Figure 5 : relation entre la contrainte de cisaillement et le gradient de vitesse pour différentes excitations magnétiques.

Q7 : Expliquer comment lire sur cette figure la valeur de la viscosité et comment celleci varie en fonction de l'excitation magnétique.

Sur la base de résultats expérimentaux, Stanway et al. ont proposé en 1987 un modèle de la force totale

consistant en un amortisseur visqueux de coefficient

en parallèle avec un système à frottement solide

constant de type Coulomb, représenté par la figure 6.

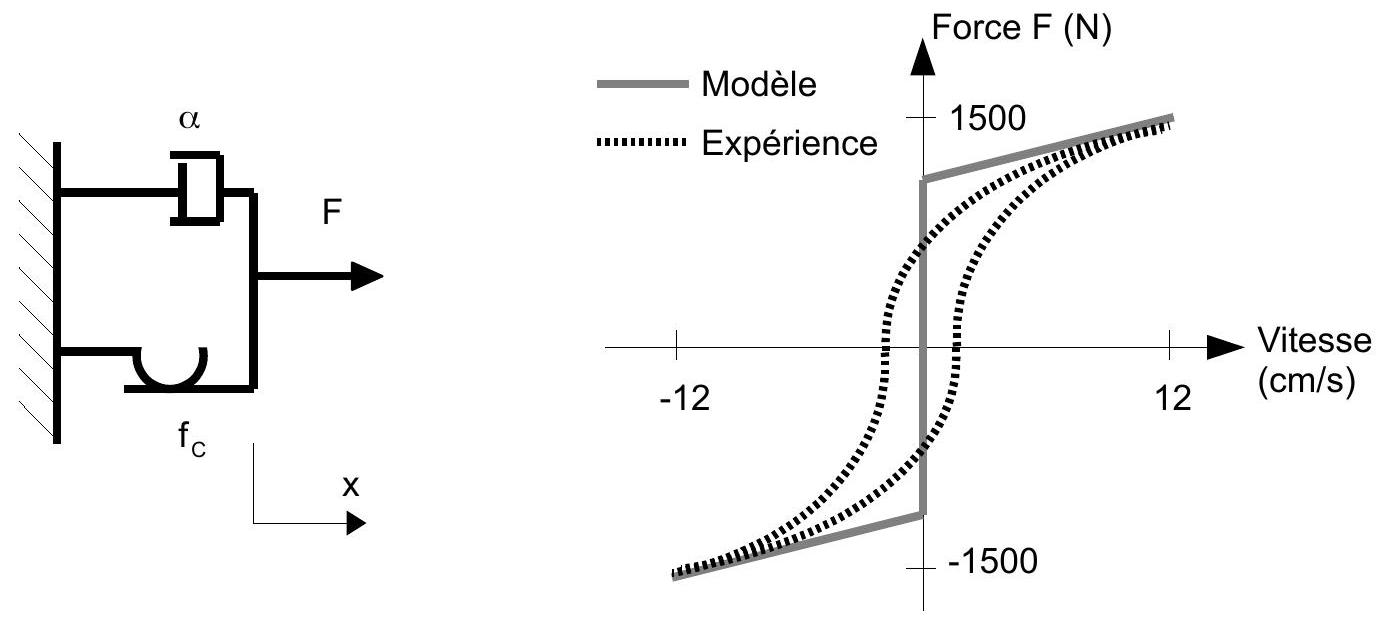
Figure 6 : modèle de Stanway et comparaison avec l'expérience.

Q8 : Justifier la pertinence de ce modèle. Donner, pour un paramétrage unidimentionnel et selon le signe de la vitesse, l'expression de la force. Évaluer les valeurs des paramètres du modèle.

Q9 : Indiquer le phénomène qui n'est pas encore pris en compte, et qui semble apparaître avec l'expérience. Commenter la qualité du modèle de Bingham.

Q10: Un second modèle a été proposé par Gamota et al. selon la figure 7. Commenter. Ce modèle conduit toutefois à des équations non linéaires difficiles à résoudre numériquement car nécessitant un pas d'intégration numérique très petit. Expliquer cette phrase.

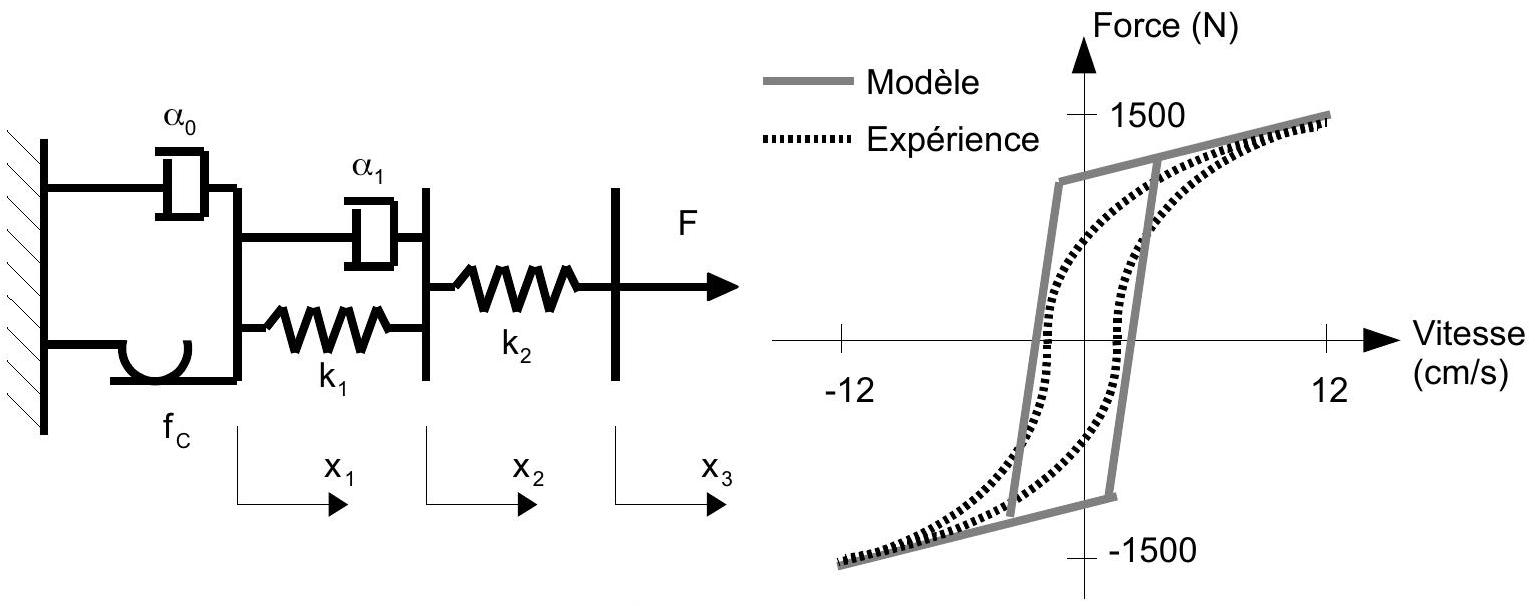
Figure 7 : modèle de Gamota et comparaison avec l'expérience.

Nombres de Hedström et Bingham

Le nombre de Hedström

est un nombre adimensionné utilisé en rhéologie pour caractériser le comportement laminaire ou turbulent d'un fluide de Bingham. Il s'écrit sous la forme

où

est le nombre de Bingham, lui aussi sans dimension, caractérisant de son côté le rapport entre les contraintes élastiques et les contraintes visqueuses (les premières étant divisées par les secondes).

Q11: Le nombre

désigne un troisième nombre adimensionné au programme de PSI. Nommer ce nombre et rappeler son expression en fonction de la vitesse caractéristique du fluide V, la dimension caractéristique L, la masse volumique du fluide

et la viscosité (dynamique) de celui-ci

. Expliquer brièvement son intérêt.

Q12 : Le nombre de Bingham s'écrit sous la forme

où

sont définis à la question précédente, T est la contrainte de cisaillement, K est une constante adimensionnée valant 1 et (

) est un quadruplet d'entiers relatifs constants, les plus petits possibles en valeur absolue. Déterminer le quadruplet. Interpréter physiquement ce nombre.

Q13 : En déduire l'expression de

. Pour une longueur caractéristique

de 1 cm , proposer un ordre de grandeur numérique de ces trois nombres à partir des documents précédents. Conclure sur la nature turbulente ou laminaire de l'écoulement, dans le cas où celui-ci serait celui d'un fluide newtonien puis de Bingham.

Conclusion

Cette partie nous a permis d'exhiber quelques propriétés et modèles de comportement d'un fluide MR. Cela a été nécessaire pour envisager son utilisation dans la conception d'un frein magnétique.

Partie 2 : conception du frein magnétique

La première partie nous a permis d'établir un modèle pour les fluides MR reliant le cisaillement

en fonction de la contrainte d'écoulement

, qui dépend de l'excitation magnétique H appliquée, de la viscosité

et du gradient de vitesse par rapport à la direction d'écoulement

Cette partie s'intéresse à une géométrie particulière de frein utilisant les fluides MR , et à son dimensionnement en vue de son utilisation pour la machine de rééducation musculaire.

Paramétrage de la géométrie du frein et hypothèses

La structure étudiée est celle du frein disque, une des plus faciles à fabriquer et qui offre un bon compromis entre ses performances et sa compacité. Dans ce frein, la partie rotorique est un disque lié à un arbre cylindrique, en rotation à l'intérieur d'une cavité statorique. Entre le stator et le rotor, on trouve le fluide MR sur les surfaces du disque rotorique, et face aux parois latérales de ce dernier, une bobine torique assurant la création de l'excitation magnétique, l'ensemble des matériaux étant supposés linéaires. Les paramètres géométriques sont indiqués sur la figure 8.

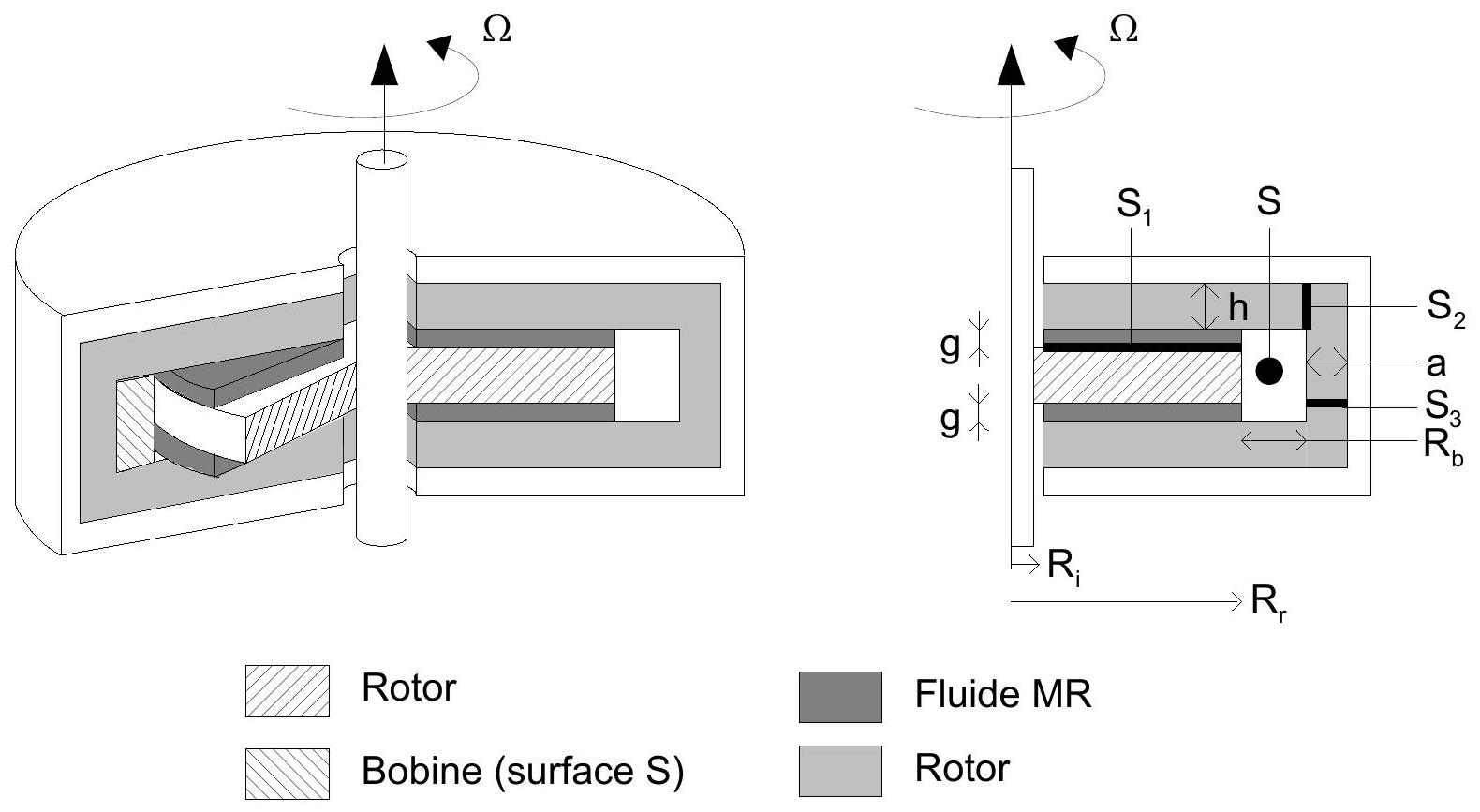
Figure 8 : paramétrage de la géométrie du frein.

La longueur

désigne l'épaisseur statorique de matériau magnétique, g celle des couches de fluide

sont les surfaces désignées sur le dessin de la figure 8 (surfaces cylindriques de révolution autour de l'arbre) et

la section de la bobine, constituée de

spires parcourue par une intensité l et d'une épaisseur radiale

. Pour simplifier, les fils seront considérés comme tous distants de

de l'axe. Le rotor tourne à une vitesse angulaire

supposée constante (régime permanent). On suppose dans toute la suite que

sont négligeables devant

et que l'excitation magnétique
est uniforme pour tout point de la surface

correspondant à la surface de contact entre le fluide MR et le rotor.

Q14 : Reproduire sur la copie le dessin de la figure 9 en indiquant et en justifiant le sens du courant électrique nécessaire pour avoir le champ proposé, ainsi que l'allure de la disposition des particules du fluide MR.

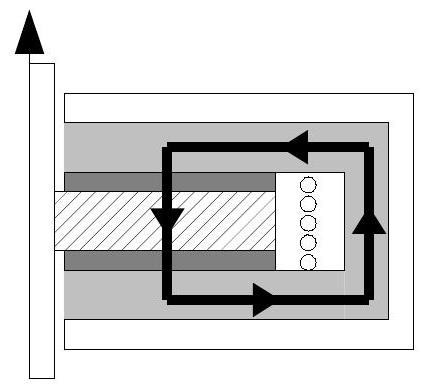
Figure 9 à reproduire sur la copie : quelques orientations des phénomènes physiques en jeu (le trait noir représente la ligne de champ).

Contrainte de cisaillement et calculs des couples

La forme de la contrainte de cisaillement proposée plus haut nous conduit à envisager le calcul de deux couples différents. Le premier, appelé « couple magnétique » et noté

, en référence au fait qu'il est lié aux phénomènes magnétiques, sera le couple dû à

. On prend pour expression de celui-ci l'intégrale :

où dA désigne un élément élémentaire de la surface active traversée par le champ d'excitation magnétique, c'est-à-dire

. Le second, noté

, est celui calculé par rapport à la contribution de la partie visqueuse du cisaillement, autrement dit et avec les mêmes notations :

On rappelle que l'on suppose la contrainte d'écoulement

uniforme sur la surface

.
Q15 : Justifier brièvement la forme commune des deux intégrales proposées.
Q16: Calculer

pour l'ensemble des surfaces actives et montrer que celui-ci peut s'écrire

. Préciser la valeur de la constante

. Expliquer alors comment choisir l'excitation pour optimiser ce couple.

Le calcul du second couple nécessite de trouver une forme d'évolution du gradient de vitesse

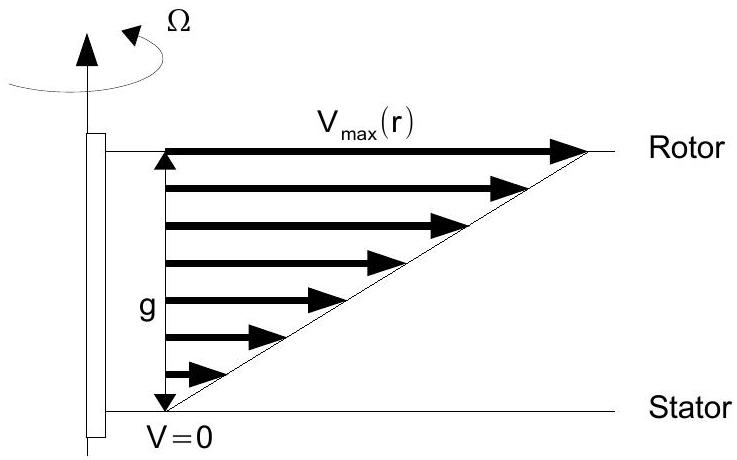
. À cette fin, on modélise le champ de vitesses du fluide MR entre le stator et le rotor, dans une coupe orthoradiale, selon la représentation de la figure 10. On fait l'hypothèse d'un écoulement laminaire et d'une vitesse de déplacement constante entre stator et rotor.

Figure 10 : modèle du champ de vitesses.

Q17 : Justifier cette double hypothèse par des raisons physiques ainsi que l'utilisation d'une coupe orthoradiale.

Q18 : Démontrer qu'en un point de

situé à une distance r de l'axe, on a

. En déduire que

s'exprime sous la forme

. On précisera la valeur de

en fonction de

et g .

Critères de performances

On s'intéresse à trois critères de performances pouvant caractériser le frein :

le rapport du couple magnétique sur le volume du stator, noté ;
le rayon du rotor, à couple fixé, déjà noté auparavant ;
la consommation électrique , correspondant aux pertes Joule dans la bobine.

On suppose que les champs et excitations magnétiques dans le fer et dans le fluide MR sont juste à saturation, ce qui assure d'après la figure 5 la plus grande valeur de

possible. On note ces grandeurs respectivement

Q19 : Expliquer physiquement l'intérêt de chacun de ces paramètres et s'ils doivent être maximisés ou minimisés.

Q20 : Rappeler la propriété fondamentale du flux magnétique et utiliser celle-ci pour relier

. Montrer également que a et

sont quasi égaux.

Q21: En négligeant

devant

, exprimer

lorsque

. Conclure sur la pertinence du choix de champs à quasi saturation.

Q22: Grâce à une hypothèse sur les perméabilités magnétiques que l'on justifiera, montrer que l'on a

Q23 : En supposant que la bobine est constituée d'un seul fil cylindrique de cuivre de conductivité

, montrer que

en précisant la valeur de la constante

en fonction de S et

Q24 : Décrire les influences de

et de g sur

. Conclure.

Dimensionnement du frein pour son usage en rééducation

On s'intéresse désormais à quelques ordres de grandeur nécessaires pour le système de rééducation que nous étudierons plus complètement plus loin. On veut obtenir un couple magnétique de

. On considère que l'on est tout juste à saturation du champ d'excitation sur la surface

et que la perméabilité magnétique relative

du fluide MR vaut 2 . On rappelle que certaines valeurs numériques se trouvent à la page 5 et on prend pour la conductivité du cuivre

. Comme précédemment, on suppose que

. Enfin, on choisit

Q25 : Calculer les champs magnétiques au niveau de l'interface rotor/fluide.
Q26 : Calculer

et en déduire le volume

du stator. La figure 5 est ici utile.
Q27 : Déterminer alors le rayon

puis

et enfin le rayon du stator. Commenter.
Q28 : Calculer la puissance électrique consommée. Commenter.

Vérification de l'hypothèse

On veut vérifier par simulation numérique la validité de l'hypothèse d'excitation (ou de champ) uniforme à l'interface rotor/fluide. Pour cela, on utilise la méthode des volumes finis, qui consiste à découper les volumes considérés (stator, rotor, bobine) en volumes élémentaires de très petite taille et à calculer le champ créé par et pour chacun puis à sommer leurs contributions en un point pour obtenir le champ total en ce point. Pour simplifier, on prend des volumes élémentaires cubiques de côté c.

Q29 : Donner la propriété des équations électromagnétiques qui permet d'assurer que le champ total est la somme des contributions élémentaires. Préciser comment varient la précision des simulations et la complexité spatiale (c'est-à-dire en mémoire) d'un tel algorithme en fonction de c. Expliquer pourquoi l'utilisation de la symétrie de révolution permet d'améliorer les temps de calculs.

Q30 : On assimile grossièrement le frein à un cylindre de 10 cm de hauteur et d'un diamètre de 6 cm . En considérant que

et que la mémoire nécessaire pour stocker la valeur du champ en chaque volume élémentaire est de 32 bits, donner en méga-octets la taille de la mémoire nécessaire aux calculs du champ en tout point du frein. On précisera les éventuelles approximations ou hypothèses. Expliquer ce qu'il se passe alors si on décide d'améliorer la précision en passant à

puis

. Conclure.

Les valeurs du champ sont ensuite calculées pour une section radiale du frein et stockées dans un fichier texte nommé donnees_champ.txt. Chaque ligne de ce fichier correspond aux valeurs d'une rangée horizontale de volumes élémentaires. Dans chaque ligne, les valeurs du champ sont séparées par une tabulation et la position de la valeur dans cette ligne correspond à la rangée verticale du volume élémentaire considéré. Le script Python suivant est alors utilisé, les numéros sur la gauche correspondant aux numéros de lignes du programme.

def recup_champ():
    fich=open('donnees_champ.txt','r')
    champ=[ ]
    for x in fich:
        interm = x.strip().split('\t')
        champ += [interm]
    return champ

La méthode strip appliquée à une chaîne de caractères renvoie une copie de la chaîne initiale dans laquelle les caractères codant un retour à la ligne (ainsi que les espaces) présents en début et en fin de chaîne sont supprimés. La méthode split décompose la chaîne initiale en une liste de sous-chaînes, le découpage s'effectuant à chaque occurrence de la chaîne passée en argument. Enfin,

correspond au codage en type string d'une tabulation.

Q31 : Expliquer ce que contient la variable champ en sortie de fonction. On précisera en particulier le type des éléments de la variable champ.

Q32 : On suppose donnés les entiers interface_hor correspondant au numéro de la ligne (numérotées à partir de zéro en haut) indiquant la position horizontale de l'interface rotor/fluide et interface_ver donnant le numéro de la colonne (numérotées à partir de zéro à gauche) délimitant la frontière rotor/bobine. Proposer et commenter un programme Python ou Scilab affichant la moyenne et la variance des valeurs du champ sur la surface

. Ce programme devra renvoyer une seule grandeur de votre choix, permettant de fournir un indicateur de la quasi-constance ou non du champ sur cette surface. On indiquera par des traits verticaux en début de ligne les indentations pour éviter toute ambiguïté dans celles-ci.

Q33 : Les résultats de simulation sont les suivants, en général et plus particulièrement pour les points situés sur la surface

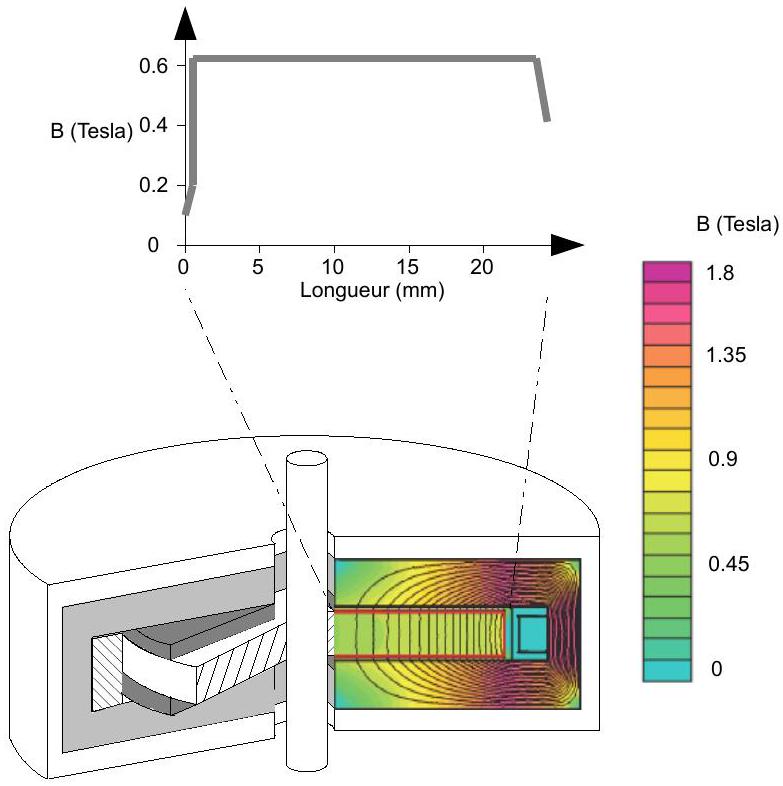
. Commenter et conclure sur la pertinence de l'hypothèse effectuée précédemment.

Figure 11 : résultats des simulations pour le calcul du champ magnétique B régnant dans le frein.

Partie 3 : étude du système de rééducation

Les parties précédentes ont permis de proposer un modèle pour le frein magnétique. L'objectif de cette partie est de montrer que ce frein, une fois inséré dans un système de rééducation musculaire, permet d'offrir au patient les différents modes de fonctionnement qui sont utiles d'un point de vue médical. Les performances attendues par un tel système de rééducation sont résumées dans le cahier des charges présent dans l'introduction du sujet.

Modélisation du système de rééducation musculaire

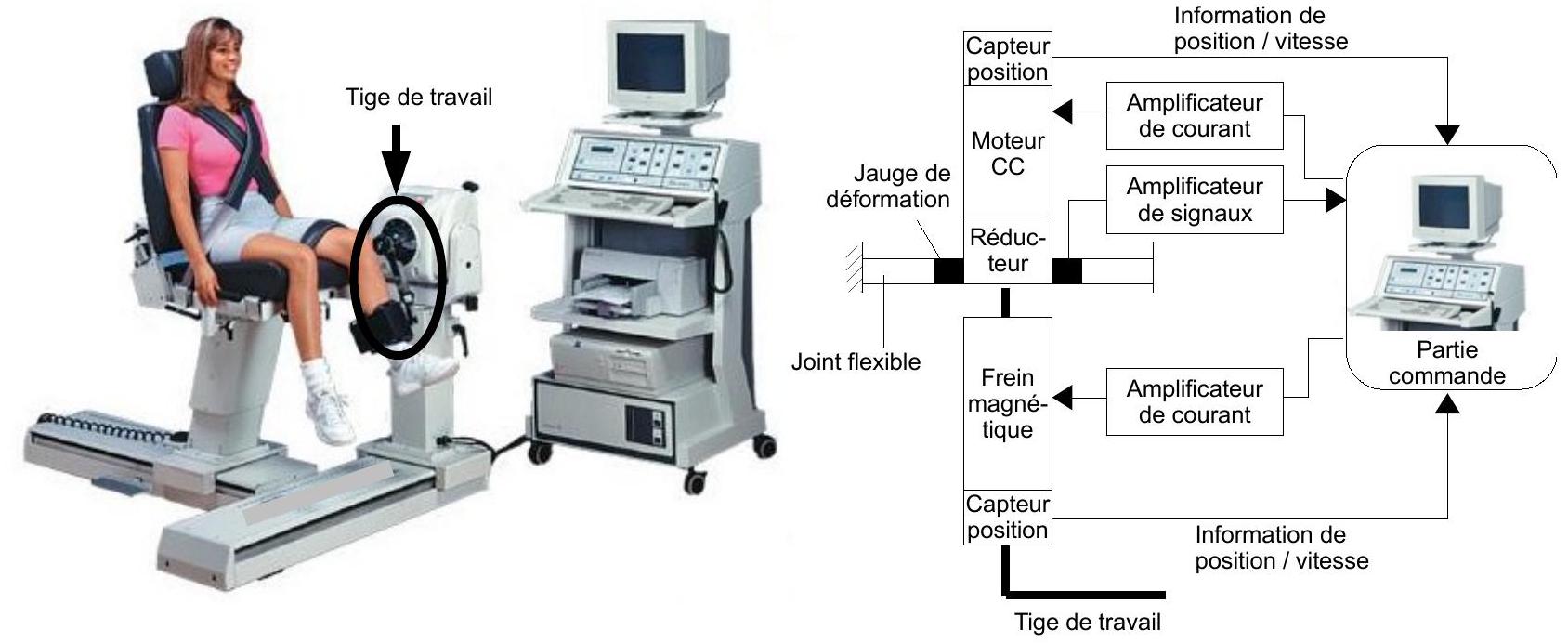
Figure 12 : solution technologique du système de rééducation par frein magnétique.

Le système de rééducation musculaire qui utilise le frein magnétique est décrit sur la figure 12. La photographie qui y est représentée montre la rééducation des muscles d'un genou. Le patient positionne son pied sur la tige de travail. Elle est mise en mouvement par un moteur à courant continu, dont la vitesse de rotation est réduite par un réducteur à engrenages. Le frein magnétique exerce un couple résistant sur l'axe en sortie du réducteur, donc sur l'axe de la tige de travail. Un capteur par jauge de déformation, associé à un joint flexible, permet de mesurer le couple exercé par le moteur. Des capteurs permettent de mesurer les positions et les vitesses angulaires du moteur et de la tige de travail, et des amplificateurs permettent d'amplifier les signaux. L'ensemble est piloté par une partie commande spécifiquement développée pour les applications médicales.

Les équations qui régissent le comportement du moteur à courant continu sont :

où

est la tension électrique d'alimentation du moteur,

l'intensité qui traverse son bobinage,

la force contre électromotrice,

la vitesse angulaire de son rotor,

le couple qu'il délivre,

sa résistance électrique interne et

l'inductance de son induit.

est une constante de proportionnalité.

Le réducteur utilisé est un réducteur à engrenages. Il est basé sur la technologie des trains épicycloïdaux. Il y a deux étages de réduction, identiques, en série. Pour le premier étage de réduction, le pignon, positionné sur l'axe du moteur, possède 12 dents. Il engrène par un contact extérieur à un satellite de 7 dents, qui lui-même engrène par un contact intérieur à une couronne dentée de 26 dents, liée au bâti. Le porte satellite du second train est la sortie du réducteur, située dans le prolongement de l'axe du moteur.

Q34 : Modéliser le réducteur à engrenages, en proposant un schéma cinématique montrant toutes les pièces qui le constituent. Respecter les dimensions relatives des pièces sur le schéma. Déterminer le rapport de réduction de ce réducteur.

Le modèle retenu pour le pilotage du système de rééducation est représenté sur la figure 13.

est l'angle de rotation de la tige de travail.

est la position angulaire souhaitée.

est le couple fourni par le frein magnétique.

est le couple fourni par l'homme qui subit une rééducation.

est le couple fourni par le moteur, via le réducteur.

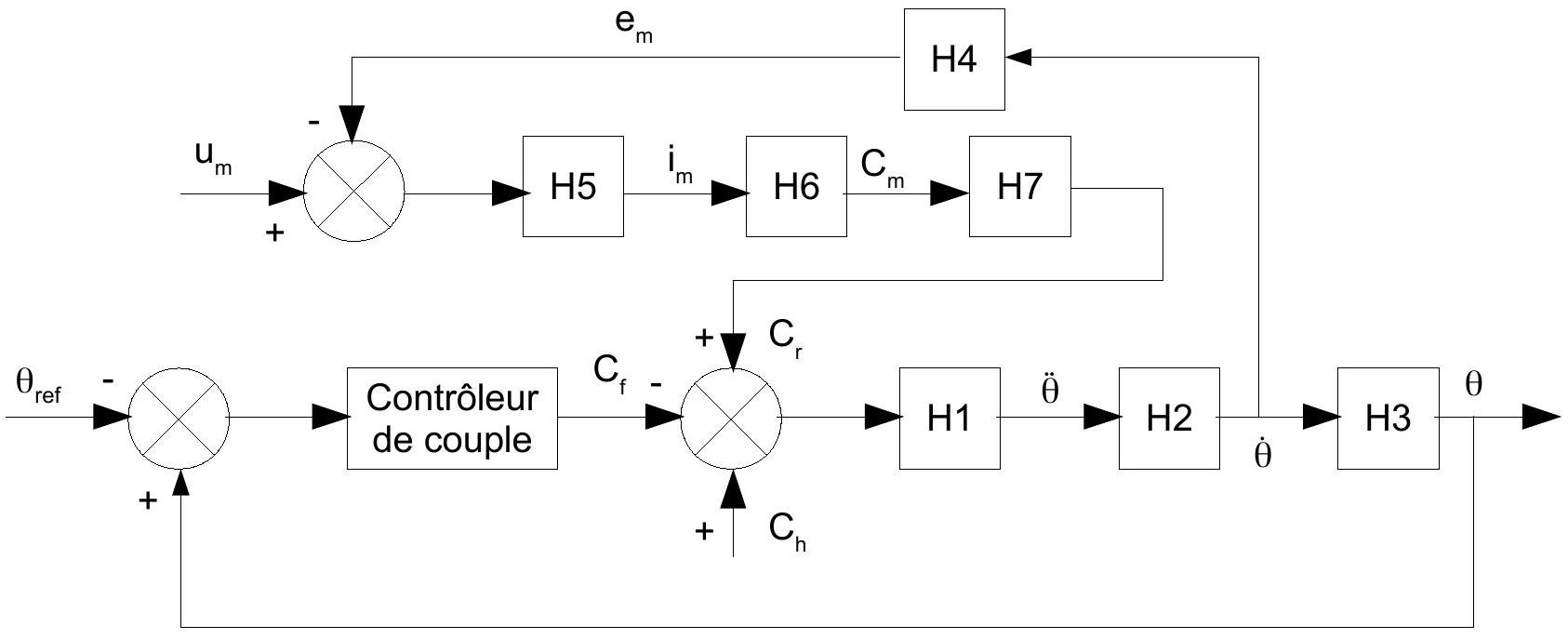
Figure 13 : modèle retenu pour pilotage du système de rééducation.

Q35 : Déterminer les expressions analytiques des fonctions H 5 et H 6 .
Q36: En notant J l'inertie des pièces en rotation ramenées sur la tige de travail, déterminer les expression analytiques des fonctions

et H 3 .

Q37 : On a

. Déterminer les valeurs numériques des fonctions H4 et H7.

Etude du mode isométrique

On étudie dans un premier temps la capacité du système à rééduquer le patient dans le mode isométrique. Pour ce mode, le fonctionnement est le suivant : le moteur positionne la tige de travail dans la position souhaitée. À partir de cette position, le moteur n'agit plus, mais le contrôleur de couple délivre un couple de freinage proportionnel à la différence entre

, avec

Q38 : Déterminer l'équation différentielle qui gère le mouvement de la tige de travail, et donc du pied du patient.

Q39: On ne demande jamais à un patient d'exercer avec son genou plus de 2 N.m. En négligeant les effets dynamiques dans l'équation précédent, indiquer si le système est capable d'atteindre la précision angulaire souhaitée pour le mode isométrique.

Etude du mode isocinématique

On étudie maintenant la capacité du système à rééduquer le patient dans le mode isocinématique. Dans ce mode, le moteur est alimenté en permanence pour imposer une vitesse de rotation à la tige de travail, à vitesse constante. Le patient exerce un couple résistant avec sa jambe, plus ou moins intensément, en fonction de sa capacité musculaire et de l'évolution de sa rééducation.

Q40 : Dans ce mode, l'évolution angulaire de la tige de travail s'exprime sous le format suivant :

. Déterminer les expressions de

en fonction de

et H 8 . H8 correspond à la fonction de transfert du contrôleur de couple.

Q41: On suppose que la fonction de transfert du contrôleur de couple est une constante de proportionnalité. Indiquer si, dans ce mode de fonctionnement, le système peut satisfaire l'exigence d'insensibilité de la vitesse de rotation aux perturbations de couple dues à l'homme.

Pour ce mode de fonctionnement, on décide d'utiliser une loi de contrôle du couple qui est représentée sur la figure 14. Un petit couple constant

est toujours ajouté au frein. Le bloc dénommé PID fournit en sortie un signal qui tient compte de

, de sa dérivée et de sa primitive, selon la loi

. La saturation limite la valeur de

à la valeur

si elle la dépasse.

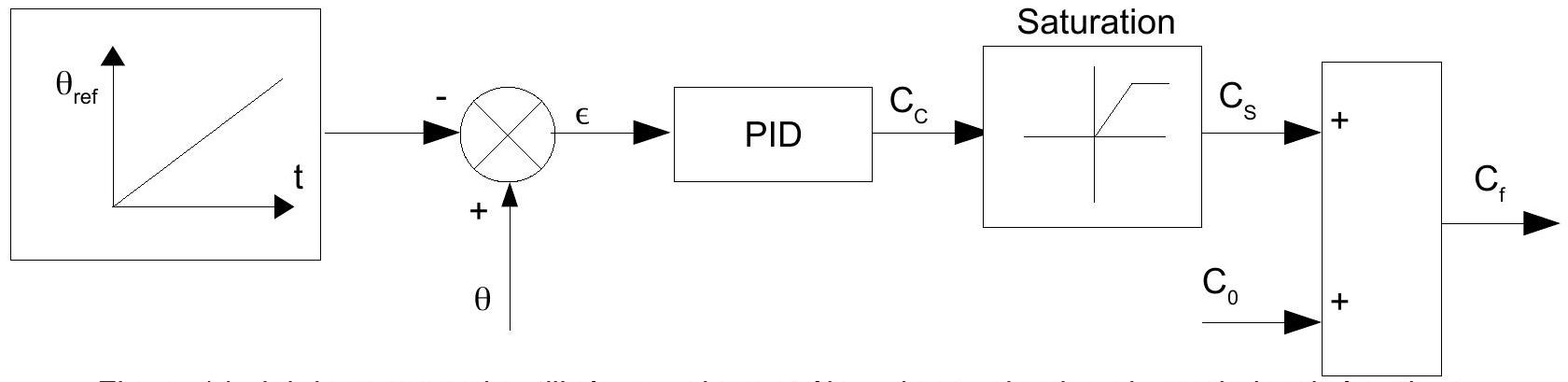
Figure 14 : loi de commande utilisée pour le contrôleur de couple, dans le mode isocinématique.

Q42 : On appelle epsilon_0 la valeur prise par є à l'instant t -dt et epsilon_1 la valeur prise par є à l'instant

, où dt est un nombre de type flottant désignant le temps d'échantillonnage. On appelle par ailleurs int_epsilon_tmdt la valeur de l'intégrale de

de l'instant 0 à l'instant t -dt. Écrire et commenter une fonction

qui retourne la valeur prise par

à l'instant t . On calculera l'intégrale par la méthode des trapèzes. Le langage utilisé sera Python ou Scilab.

La figure 15 montre l'évolution des grandeurs physiques lors de l'utilisation du système dans son mode isocinématique.

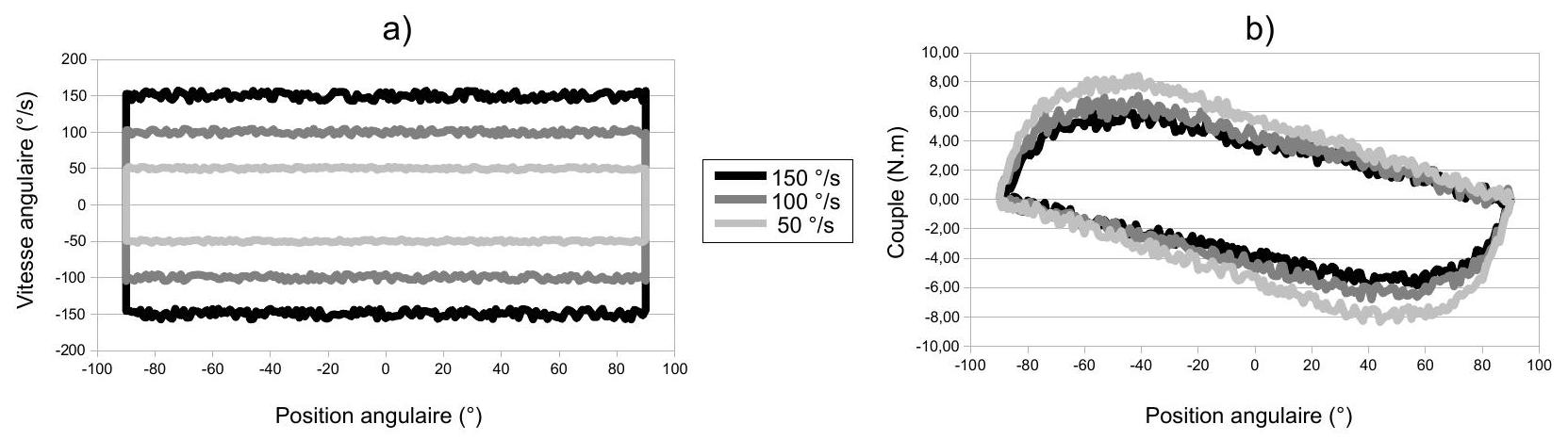
Figure 15 : mode isocinématique. Gauche : évolution de la vitesse angulaire en fonction de la position angulaire de la tige de travail. Droite : évolution du couple délivré par le patient en fonction de la position angulaire de la tige de travail.

Q43 : Indiquer la raison pour laquelle la mesure de l'angle ne se fait pas sur une plage de position angulaire plus grande que la plage [

;

]. Expliquer pourquoi les vitesses sont mesurées positivement et négativement.

Q44: Indiquer si le système est capable de répondre au cahier des charges, concernant la précision de

sur la vitesse angulaire en régime permanent.

Etude du mode isotonique

Pour faire travailler le patient en mode isotonique, il suffit de permettre au système de générer le couple souhaité. La figure 16 montre le modèle de la loi de commande retenue pour ce mode. On réalise un asservissement du couple. La fonction de transfert du frein est, en première approximation, modélisée par une fonction du premier ordre de gain

et de constante de temps

. Le correcteur utilisé est

Figure 16 : modèle de la loi de commande retenue pour le mode isotonique.

Q45 : Indiquer si le système satisfait au cahier des charges en terme de précision.

Q46 : Déterminer les valeurs de

pour obtenir la marge de phase souhaitée dans le cahier des charges, à la pulsation

Q47 : Indiquer si, pour ce réglage du correcteur, la marge de gain satisfait le cahier des charges.

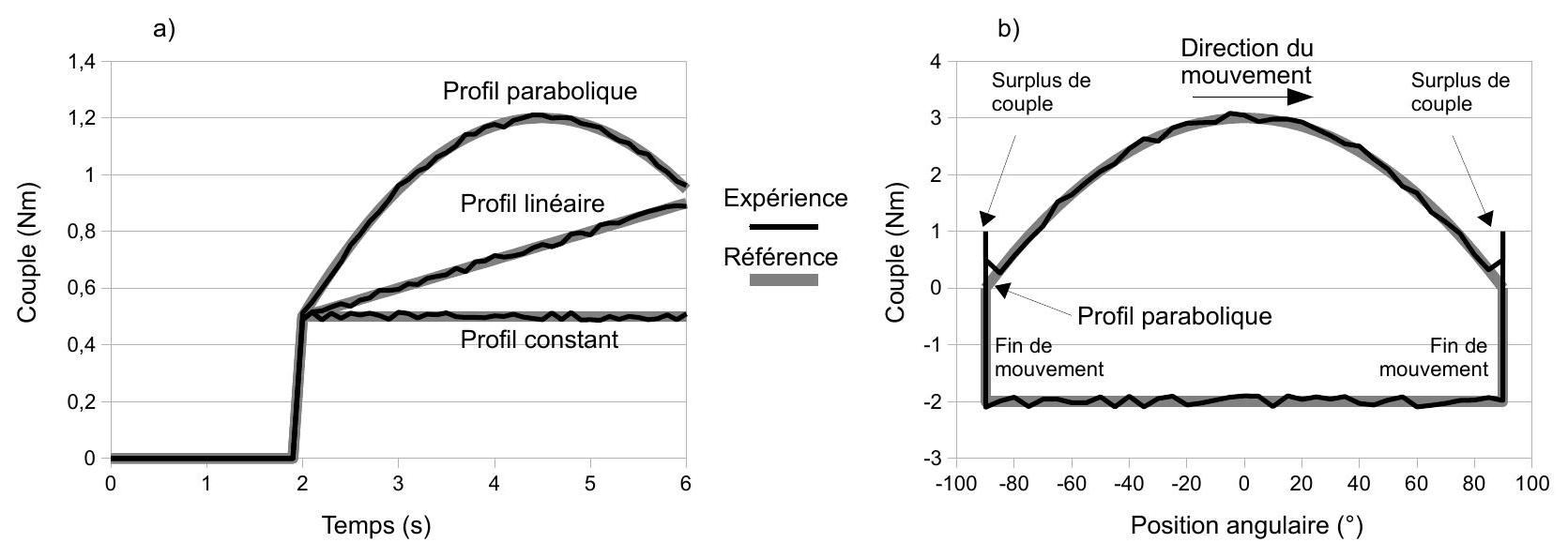
Figure 17 : évolution du couple en mode isotonique. Gauche : évolution du couple au cours du temps, pour différents profils d'évolution souhaités. Droite : évolution du couple en fonction de la position angulaire, pour un profil d'évolution souhaite.

L'évolution du couple, en fonction de différents profils d'évolution souhaités, est représentée sur la figure 17.

Q48 : Indiquer si l'évolution du couple au cours du temps, en fonction des différents profils, est cohérente par rapport au choix du correcteur retenu. Expliquer une origine possible pour le surplus de couple visible sur la figure 17 (b).

Conclusion

Cette étude, qui prend fin ici, a permis de montrer que le système de rééducation musculaire basé sur un frein magnétique permet de rééduquer le patient selon les différents modes isométrique, isocinématique et isotonique. Il représente ainsi un système technologique intéressant pour le monde de la médecine.

Remerciements

Les éléments de cette étude ont été extraits du travail du docteur More Thomas AVRAAM, à I'Université libre de Bruxelles.