J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

X ENS Option Informatique MP 2016

Satisfiabilité des formules booléennes

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo x-ens
🔗 Explorer
Banque
X-ENS
Année
2016
Filière
MP
Matière
Info
X-ENS MPX-ENS 2016MP InfoInfo 2016
2025_08_29_ad736b8059be40aba879g

COMPOSITION D'INFORMATIQUE - A - (XULCR)

(Durée : 4 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Le langage de programmation sera obligatoirement Caml.

Satisfiabilité des formules booléennes

Nous nous intéressons ici au problème bien connu de la satisfiabilité des formules booléennes, appelé SAT dans la littérature. Historiquement, SAT a joué un rôle prépondérant dans le développement de la théorie de la complexité. De nos jours il intervient dans de nombreux domaines de l'informatique où des problèmes combinatoires difficiles apparaissent, comme la vérification formelle, la recherche opérationnelle, la bioinformatique, la cryptologie, l'apprentissage automatique, la fouille de données, et bien d'autres encore. Signe de son importance, SAT et ses variantes ont leur propre conférence internationale qui se tient tous les ans depuis près de 20 ans.
Ce sujet se concentre sur une version restreinte de SAT, appelée -SAT, dans laquelle les formules booléennes considérées en entrée sont en forme normale conjonctive avec au plus littéraux par clause. Le but est d'apporter aux candidats les rudiments de l'analyse de la complexité de -SAT, en proposant des approches efficaces pour des valeurs spécifiques de ainsi qu'une approche générale pour les valeurs de arbitraires. Le sujet s'articule donc naturellement autour des differentes valeurs de pour la partie I, pour la partie II, pour la partie III. La partie IV fait le lien avec le problème SAT lui-même.

Préliminaires

Cette partie préliminaire introduit formellement les concepts et résultats utiles pour l'analyse. Par complexité (en temps) d'un algorithme on entend le nombre d'opérations élémentaires (comparaison, addition, soustraction, multiplication, division, affectation, test, etc) nécessaires à l'exécution de dans le cas le pire. Lorsque ce nombre dépend d'un ou plusieurs paramètres , on dit que a un temps d'exécution en s'il existe une constante telle que, pour toutes les valeurs de suffisamment grandes (c'est-à-dire plus grandes qu'un certain seuil), pour toute instance du problème de paramètres , le nombre d'opérations élémentaires est au plus . On dit que la complexité est linéaire quand est une fonction linéaire des paramètres . De même, on dit que la
complexité est polynomiale quand est une fonction polynomiale des paramètres. Sauf mention contraire dans l'énoncé, le candidat n'aura pas à justifier de la complexité de ses algorithmes. Toutefois il devra veiller à ce que cette complexité ne dépasse pas les bornes prescrites.
Pour la programmation proprement dite, en plus des fonctionnalités de base du langage Caml le candidat pourra utiliser les fonctions suivantes sans les programmer :
- do_list: ('a -> unit) -> 'a list -> unit
    do_list f [a1; a2; ...; an] équivaut à begin f a1; f a2; ...; f an; () end
- map: ('a -> 'b) -> 'a list -> 'b list
    map f [a1; a2; ...; an] renvoie la liste [f a1;f a2; ...; f an]
- it_list: ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a
    it_list f a [b1; ...; bn] renvoie la valeur de f (... (f (f a b1) b2) ...)
- list_it: ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b
    list_it f [a1; ...; an] b renvoie la valeur de f a1 (f a2 (... (f an b) ...))
Formules booléennes. Une variable booléenne est une variable prenant ses valeurs dans l'ensemble {Vrai, Faux}. Une formule booléenne s'obtient en combinant des variables booléennes et des connecteurs logiques Et (noté ), Ou (noté ), Non (noté ), selon la grammaire suivante, donnée directement dans le langage Caml :
type formule =
    |Var of int
    |Non of formule
    |Et of formule * formule
    |Ou of formule * formule;;
Ainsi les formules booléennes sont représentées par des structures arborescentes en machine, appelées arbres d'expression dans la suite. Voir la figure 1 pour un exemple.
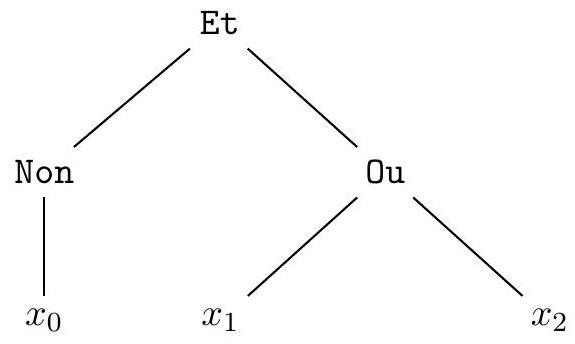
Figure 1 - L'arbre d'expression associé à la formule de taille 6.
À noter que les variables d'une formule sont indexées par des entiers, d'où la ligne Var of int dans la définition du type formule. Par défaut ces entiers seront supposés positifs ou nuls, contigus, et commençant par 0 . Ainsi, les variables de seront dénotées par exemple . La taille de est le nombre total de variables booléennes et de connecteurs logiques qui la composent. C'est donc le nombre total de nœuds composant l'arbre d'expression associé, et on a naturellement .
Valuations et équivalence logique. Étant données variables booléennes , une valuation est une application {Vrai, Faux . Étant donnée une formule utilisant ces variables, le résultat de l'évaluation de sur , noté , est obtenu en affectant la valeur à chaque variable . Deux formules et utilisant les variables booléennes sont dites logiquement équivalentes si pour toute valuation Vrai, Faux .
Propriétés des connecteurs logiques. Rappelons que le connecteur est involutif, c'est-à-dire que pour toute formule :
  • est logiquement équivalente à .
Par ailleurs, en plus d'être commutatifs et associatifs, les connecteurs logiques et sont distributifs, c'est-à-dire que pour toutes formules et :
  • est logiquement équivalente à ,
  • est logiquement équivalente à .
Dans ce sujet nous adoptons la convention que le connecteur est prioritaire sur et , ce qui permet par exemple d'écrire au lieu de comme dans la figure 1.
Les lois de De Morgan décrivent la manière dont et interagissent avec . Pour toutes formules et :
  • est logiquement équivalente à ,
  • est logiquement équivalente à .
Le problème SAT. Étant donnée une formule à variables , le problème SAT consiste à déterminer s'il existe une valuation {Vrai, Faux} telle que Vrai. Dans l'affirmative, la formule est dite satisfiable. Dans la négative, est dite insatisfiable. Par exemple, la formule de la figure 1 est satisfiable, tandis que est insatisfiable.
Question 1 Pour chaque formule qui suit, dire si elle est satisfiable ou non, sans justification :
a)
b)
c)
d)
Forme normale conjonctive. Dans la suite nous utiliserons essentiellement des formules écrites sous la forme suivante, appelée forme normale conjonctive (FNC) :
où chaque littéral est soit une variable booléenne , soit sa négation , et où les littéraux sont regroupés en clauses disjonctives . Par exemple, les formules a), b) et d) de la question 1 sont des FNC.
Une FNC est appelée lorsque chaque clause a au plus littéraux, c'est-à-dire que pour tout dans l'équation (1). Notez qu'alors la formule est également
une -FNC pour tout . Par exemple, les formules a), b) et d) de la question 1 sont des . La variante de SAT appelée -SAT prend uniquement en entrée des formules en . C'est cette variante qui nous intéresse dans ce sujet. Elle est équivalente à SAT du point de vue de la théorie de la complexité quand , comme nous le verrons dans la partie IV.
En machine nous représenterons les FNC sous la forme de listes de listes. Plus précisément, une FNC sera une liste de clauses et chaque clause sera une liste de littéraux :
type litteral =
    |V of int (* variable *)
    |NV of int;; (* négation de variable *)
type clause == litteral list;;
type fnc == clause list;;
Ainsi, une formule en -FNC sera représentée par une liste (de taille arbitraire) de listes de taille au plus chacune.
Question 2 Écrire une fonction var_max qui prend en entrée une FNC et renvoie le plus grand indice de variable utilisé dans la formule. La complexité de la fonction doit être linéaire en la taille de .
var_max: fnc -> int

Partie I. Résolution de 1-SAT

Commençons pas le cas le plus simple, à savoir . Ici chaque clause de la FNC est formée d'un unique littéral et donc impose un unique choix possible d'affectation pour la variable : soit et dans ce cas doit valoir Vrai, soit et dans ce cas doit valoir Faux. La formule est alors satisfiable si et seulement s'il n'y a pas de contradiction dans les choix d'affectation de variables imposés par ses différentes clauses. Afin d'effectuer ce test efficacement, nous allons maintenir un tableau où chaque case correspondra à une variable de la formule (de même indice que la case) et où les valeurs seront des triléens : vrai, faux, ou indéterminé. Pour cela nous définissons le type trileen ci-dessous :
type trileen =
    |Vrai
    |Faux
    |Indetermine;;
Grâce au tableau de triléens, à chaque littéral rencontré on peut déterminer en temps constant si la variable est déjà affectée ou non, et dans l'affirmative, si sa valeur d'affectation est compatible avec celle imposée par .
Question 3 Écrire une fonction un_sat qui prend en entrée une FNC , supposée être une 1-FNC, et qui renvoie un booléen valant true si et seulement si est satisfiable. La complexité de la fonction doit être linéaire en la taille de .
un_sat: fnc -> bool

Partie II. Résolution de 2-SAT

Nous venons de voir que 1-SAT est un problème facile puisque résoluble en temps linéaire. Nous allons maintenant voir que 2-SAT est également linéaire, bien que son traitement efficace nécessite plus de travail d'analyse et de codage. Nous allons en effet montrer comment réduire les instances de 2-SAT à la recherche de composantes fortement connexes dans un graphe orienté. Ce dernier problème a un intérêt en soi et fait l'objet de la sous-partie II.1. La réduction proprement dite sera détaillée dans la sous-partie II.2.

II. 1 Recherche de composantes fortement connexes dans un graphe orienté

Soit un graphe orienté. Rappelons qu'un tel objet est défini par deux ensembles finis : l'ensemble des sommets (ou nœuds) et l'ensemble des arêtes orientées (ou arcs orientés). Chaque arête de relie deux sommets dans un ordre précis. C'est donc un élement de ( ). La taille du graphe est , où et désignent respectivement le nombre de sommets et le nombre d'arêtes.
Par défaut les sommets de sont indexés par les entiers 0 à inclus. Ainsi, on pourra les désigner par . En machine nous représentons par listes d'adjacence, plus précisément par un tableau de listes d'entiers :
type graphe int list vect;;
où les indices du tableau correspondent à ceux des nœuds du graphe et où la liste associée à la case d'indice dans le tableau contient les indices des successeurs du noeud dans le graphe, c'est-à-dire les entiers tels que . Voir la figure 2 pour une illustration.
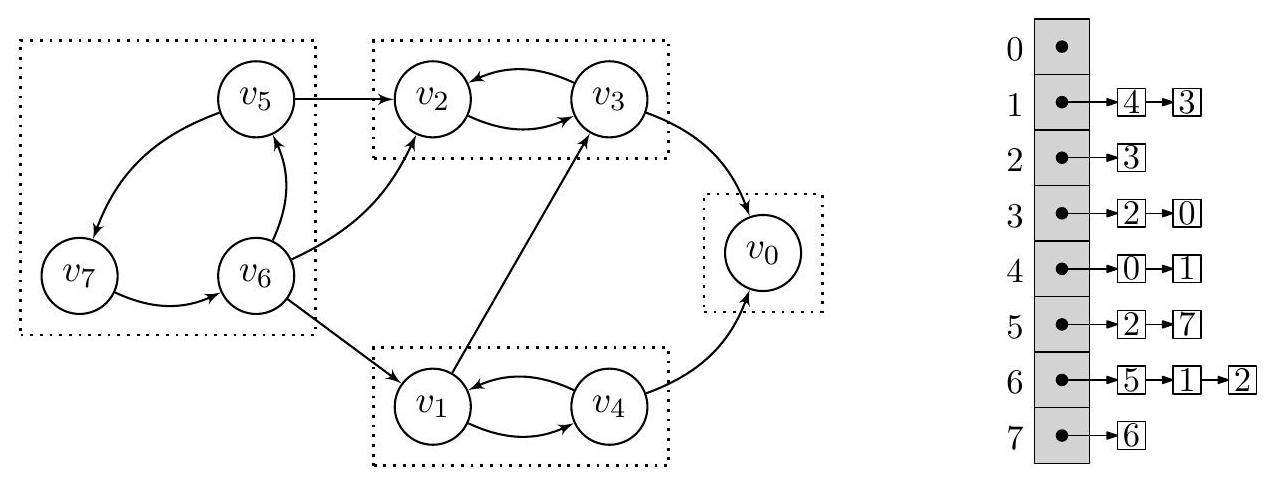
Figure 2 - Un exemple de graphe orienté avec, à droite, une représentation par listes d'adjacence. Les composantes fortement connexes du graphe sont encadrées en pointillés.
Rappelons qu'un chemin d'un sommet à un sommet dans est une suite finie de sommets telle que pour tout . Ici, désigne la longueur du chemin. Par exemple, le graphe de la figure 2 contient le chemin de longueur 6 et le chemin ( ) de longueur nulle, mais pas le chemin de longueur 1 .
Une composante fortement connexe de est un sous-ensemble de ses sommets, maximal pour l'inclusion, tel que pour tout couple de sommets il existe un chemin de à dans . Voir la partie gauche de la figure 2 pour une illustration. Le calcul des composantes
fortement connexes de peut se faire naïvement en testant l'existence d'un chemin dans le graphe pour chaque couple de sommets. Cette approche revient à effectuer un parcours complet du graphe au départ de chaque sommet, par conséquent elle est trop coûteuse en temps. D'autres approches permettent de faire le même calcul en temps linéaire en la taille du graphe, dont celle de Kosaraju-Sharir que nous allons maintenant étudier. L'algorithme procède en deux étapes :
a) Il effectue un parcours en profondeur récursif de et relève, pour chaque nœud visité , l'instant de fin de traitement du nœud. Cet instant se situe à la fin de l'exécution de la fonction de parcours sur le nœud , après le retour des appels récursifs sur ses successeurs dans le graphe. Le code Caml correspondant est fourni ci-dessous : la fonction dfs_tri prend un graphe g en entrée et renvoie la liste des indices des sommets du graphe, ordonnée dans l'ordre inverse de leurs instants de fin de traitement (notez la ligne 8, qui insère l'indice du sommet courant en tête de liste au moment de la fin de son traitement par la fonction de parcours récursif dfs_rec) :
let dfs_tri g =
    let deja_vu = make_vect (vect_length g) false in
    let resultat = ref [] in
    let rec dfs_rec i =
        if not deja_vu.(i) then begin
            deja_vu.(i) <- true;
            do_list dfs_rec g.(i); (* voir page 2 pour la définition de do_list *)
            resultat := i :: !resultat;
        end in
    for i = 0 to vect_length g - 1 do dfs_rec i done;
    !resultat;;
dfs_tri: graphe -> int list
b) Il effectue un deuxième parcours en profondeur, cette fois du graphe obtenu en renversant le sens de toutes les arêtes de . Les différents sommets de départ du parcours sont choisis non pas dans un ordre arbitraire comme à l'étape a) mais dans l'ordre décroissant des instants . Pour chaque sommet de départ , l'ensemble des sommets visités par le parcours en profondeur de à partir de forme une composante fortement connexe du graphe initial .
Illustrons l'algorithme sur l'exemple de la figure 2 :
a) Le parcours en profondeur du graphe initial , en considérant les sommets de départ par ordre croissant d'indice comme dans la fonction dfs_tri (ligne 10), choisit d'abord comme point de départ. Le sous-graphe parcouru est alors le sommet seul. Ensuite, le parcours reprend au sommet et visite le sommet , puis revient à et visite puis , puis revient à puis à et s'arrête. Enfin, le parcours reprend au sommet et visite les sommets puis avant de revenir à puis à pour s'arrêter. Les instants de fin de traitement des sommets lors du parcours récursif sont donc dans l'ordre suivant :
La liste renvoyée par dfs_tri est donc .
b) Le parcours en profondeur du graphe renversé , en considérant les sommets de départ dans l'ordre inverse de (2), choisit d'abord et visite ainsi et , ce qui donne la composante . Ensuite le parcours reprend du sommet et visite ainsi , ce qui donne la composante . Ensuite le parcours reprend du sommet et visite ainsi , ce qui donne la composante . Enfin le parcours reprend du sommet et s'arrête là, ce qui donne la composante .
Codage de l'algorithme. L'étape a) de l'algorithme est déjà codée dans dfs_tri.
Question 4 Justifier formellement la complexité linéaire (en la taille du graphe) de la fonction dfs_tri. Rappelons que la taille du graphe est la somme de son nombre de sommets et de son nombre d'arêtes.
Pour pouvoir effectuer l'étape b) il faut d'abord renverser le graphe.
Question 5 Écrire une fonction renverser_graphe qui prend en entrée un graphe et qui renvoie un autre graphe dans lequel les sommets sont les mêmes et le sens de toutes les arêtes est inversé. La complexité de la fonction doit être linéaire en la taille du graphe fourni en entrée.
renverser_graphe: graphe -> graphe
Question 6 Écrire une fonction dfs_cfc qui code l'étape b) de l'algorithme. Elle prend en entrée le graphe renversé construit à la question précédente, ainsi que la liste d'entiers renvoyée par dfs_tri sur le graphe de départ. Elle renvoie une liste dans laquelle chaque élément est une liste d'entiers contenant les indices des sommets d'une composante fortement connexe du graphe, sans doublons. La complexité de la fonction doit être linéaire en la taille du graphe.
dfs_cfc: graphe -> int list -> int list list
Question 7 Écrire enfin une fonction cfc qui prend en entrée un graphe et qui renvoie une liste de listes d'entiers contenant l'ensemble des composantes fortement connexes du graphe, chaque composante fortement connexe étant stockée dans l'une des listes d'entiers. La complexité de la fonction doit être linéaire en la taille du graphe.
cfc: graphe -> int list list
Correction de l'algorithme. Nous dirons qu'une composante fortement connexe de est subordonnée à une autre composante fortement connexe s'il existe des sommets et et un chemin de à dans . Comme et sont des composantes fortement connexes, cela revient à dire qu'il existe des chemins dans de n'importe quel sommet de à n'importe quel sommet de .
Question 8 Montrer que la relation être subordonnée à est une relation d'ordre (pas forcément totale) sur l'ensemble des composantes fortement connexes de .
À chaque composante fortement connexe on associe un instant de fin de traitement comme ceci :
où les sont définis comme à l'étape a) de l'algorithme. Par exemple, dans l'exemple de la figure 2 on a :
Question 10 Montrer que l'ordre total sur les composantes fortement connexes de défini par les instants de fin de traitement est compatible avec l'ordre partiel être subordonnée , c'est-à-dire que pour toutes composantes et telles que est subordonnée à , on a .
Question 11 En utilisant les résultats des questions précédentes, montrer que le parcours en profondeur du graphe renversé à l'étape b) de l'algorithme extrait les composantes fortement connexes de les unes après les autres, dans l'ordre des décroissants. Pour cela on pourra s'appuyer sur les observations simples suivantes sans les démontrer :
  • Les composantes fortement connexes de sont les mêmes que celles de .
  • La relation d'ordre être subordonnée à dans est inversée par rapport à celle dans .

II. 2 Des composantes fortement connexes à 2-SAT

La réduction d'une instance de 2-SAT à un calcul de composantes fortement connexes dans un graphe repose sur l'observation simple que toute clause ( ) est logiquement équivalente à , elle-même équivalente à sa contraposée . Lorsqu'une clause est formée d'un seul littéral , il suffit de l'exprimer sous la forme équivalente ( ), ce qui donne ( ) , qui est sa propre contraposée. Cette observation suggère la procédure suivante pour construire un graphe orienté à partir d'une 2-FNC à variables (notées ) :
  • Pour chaque variable on ajoute les sommets et à , qui représentent respectivement le littéral et le littéral .
  • Pour chaque clause de type ( ) on ajoute une arête à , soit du sommet au sommet si , soit du sommet au sommet si .
  • Pour chaque clause de type ( ) où les littéraux contiennent des variables distinctes, on ajoute deux arêtes à , choisies en fonction des cas suivants :
  • si et , alors on ajoute les arêtes et ,
  • si et , alors on ajoute les arêtes ( ) et ( ),
  • si et , alors on ajoute les arêtes ( ) et ( ),
  • si et , alors on ajoute les arêtes ( ) et ( ).
  • Enfin, pour chaque clause de type ( ) où les littéraux contiennent la même variable , soit on élimine directement la clause si elle est de la forme ( ) ou ( ), soit on se ramène au cas d'une clause de type ( ) si elle est de la forme ( ) ou ( ).
    Par exemple, sur la formule , la procédure donne un graphe avec quatre sommets : , et trois arêtes : , comme illustré dans la figure 3 .
Question 12 Donner le résultat de la procédure ci-dessus sur la formule .
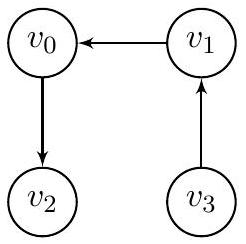
Question 13 Écrire une fonction deux_sat_vers_graphe qui prend en argument une FNC , supposée être une 2-FNC, et qui renvoie le graphe obtenu par la procédure ci-dessus. On
Figure 3 - Le graphe obtenu à partir de la formule .
pourra utiliser la fonction var_max codée à la question 2 . Pour simplifier, on supposera qu'aucune clause n'est répétée dans et qu'aucune clause n'est de type ( ) où contiennent la même variable . La complexité de la fonction deux_sat_vers_graphe doit être linéaire en la taille de .
deux_sat_vers_graphe: fnc -> graphe
Question 14 Supposons que la 2-FNC initiale soit satisfiable et soit une valuation telle que Vrai. Montrer qu'alors, pour tous sommets situés dans une même composante fortement connexe de , les variables booléennes et correspondantes vérifient si est pair et si est impair. Ici la notation désigne la partie entière inférieure.
Question 15 En déduire que si est satisfiable, alors il n'existe pas de variable dont les deux sommets correspondants et se trouvent dans la même composante fortement connexe du graphe .
Réciproquement, on peut montrer que s'il n'existe pas de variable de dont les deux sommets correspondants et se trouvent dans la même composante fortement connexe du graphe , alors en attribuant la même valeur booléenne à tous les littéraux impliqués dans chacune des composantes fortement connexes de , on construit une valuation telle que Vrai. Ceci fournit un critère simple pour décider de la satisfiabilité de .
Question 16 Écrire une fonction deux_sat qui prend en entrée une FNC , supposée être une 2-FNC, et qui renvoie un booléen indiquant si est satisfiable ou non. La complexité de la fonction doit être linéaire en la taille de .
deux_sat: fnc -> bool

Partie III. Résolution de -SAT pour arbitraire

Nous allons maintenant décrire un algorithme pour la résolution de -SAT dans le cas général. Le principe de base de l'algorithme est de faire une recherche exhaustive sur l'ensemble des valuations possibles des variables de la formule. Pour chaque valuation considérée on évalue la formule : si le résultat est Vrai alors on renvoie Vrai, si le résultat est Faux alors on rejette la valuation courante et on passe à la suivante. L'algorithme est en fait un peu plus malin que cela : il évalue la formule également pour des valuations partielles et décide, soit d'accepter la valuation partielle courante si le résultat de l'évaluation est déjà Vrai, soit de la rejeter précocement si le
résultat est déjà Faux, soit enfin de compléter la construction de la valuation si le résultat de l'évaluation est encore Indetermine.
Pour coder les valuations partielles en machine nous allons utiliser des tableaux de triléens. Rappelons que le type trileen a été introduit dans la partie I. Ce type nous fait travailler non plus dans l'algèbre binaire de Boole, où les variables prennent leurs valeurs parmi les deux booléens habituels, mais dans l'algèbre ternaire dite de Kleene, où les variables prennent leurs valeurs parmi les trois triléens. Les nouvelles tables de vérité des connecteurs et sont données dans la figure 4.
Vrai Indét. Faux
Vrai Vrai Indét. Faux
Indét. Indét. Indét. Faux
Faux Faux Faux Faux
Vrai Indét. Faux
Vrai Vrai Vrai Vrai
Indét. Vrai Indét. Indét.
Faux Vrai Indét. Faux
Vrai Faux
Indét. Indét.
Faux Vrai
Figure 4 - Tables de vérité des connecteurs logiques usuels sur les triléens. Les valeurs d'affectation des variables sont respectivement Vrai, Indét(erminé), Faux.
Question 17 Écrire trois fonctions : et, ou, non, qui codent respectivement les connecteurs logiques sur les triléens. La complexité de chaque fonction doit être constante.
et: trileen -> trileen -> trileen
ou: trileen -> trileen -> trileen
non: trileen -> trileen
Supposons maintenant que les variables d'une FNC prennent leurs valeurs parmi les triléens. Une récurrence immédiate montre alors qu'une clause disjonctive de la formule vaut Vrai quand l'un au moins de ses littéraux vaut Vrai, Faux quand tous ses littéraux valent Faux, et Indetermine dans tous les autres cas. Une autre récurrence immédiate montre que la FNC elle-même vaut Vrai quand toutes ses clauses valent Vrai, Faux quand au moins l'une de ses clauses vaut Faux, et Indetermine dans tous les autres cas.
Question 18 En vous appuyant sur la remarque ci-dessus et sur les fonctions de la question 17, écrire une fonction eval qui prend en entrée une FNC ainsi qu'un tableau de triléens , et qui renvoie un triléen indiquant si le résultat de l'évaluation de sur la valuation partielle fournie dans est Vrai, Faux ou Indetermine. On supposera que a la bonne taille. La complexité de la fonction doit être linéaire en la taille de la formule.
eval: fnc -> trileen vect -> trileen
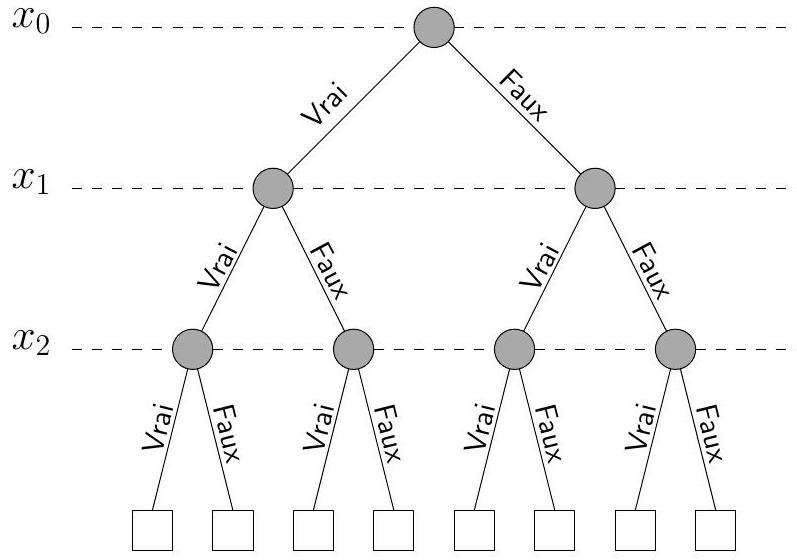
Nous pouvons maintenant décrire l'algorithme de recherche exhaustive avec terminaison précoce. Pour itérer sur l'ensemble des valuations nous utilisons une approche récursive consistant à parcourir en profondeur les branches d'un arbre binaire sans le construire explicitement. Chaque niveau de l'arbre correspond à l'affectation de la variable , comme illustré dans la figure 5 pour le cas de 3 variables.
Figure 5 - Arbre parcouru lors de la recherche exhaustive parmi les valuations des variables .
Au départ la valeur Indetermine est affectée à toutes les variables. Le parcours commence à la racine. À chaque nœud de l'arbre visité, avant toute affectation de la variable correspondante, un appel à la fonction eval est fait pour tester si le résultat de l'évaluation est :
  • Vrai, auquel cas l'exploration s'arrête et la formule est satisfiable,
  • Faux, auquel cas l'exploration de la branche courante de l'arbre s'interrompt prématurément pour reprendre au niveau du parent du nœud courant,
  • Indetermine, auquel cas l'exploration de la branche courante de l'arbre se poursuit normalement.
Comme indiqué précédemment, pour stocker la valuation partielle courante on utilise un tableau de triléens dans lequel les variables non encore affectées prennent la valeur Indetermine.
Question 19 Écrire une fonction k_sat qui prend en entrée une FNC et qui renvoie un booléen valant true si est satisfiable et false sinon. La fonction doit coder la méthode de recherche exhaustive avec terminaison précoce décrite ci-dessus. Sa complexité doit être en , où est la taille de . En outre, un soin particulier doit être apporté à la clarté du code, dans lequel il est recommandé d'insérer des commentaires aux points clés.
k_sat: fnc -> bool

Partie IV. De -SAT à SAT

Dès le début du sujet nous avons laissé de côté le problème SAT au profit de sa variante -SAT. Comme toute instance du deuxième problème est également une instance du premier, -SAT est a priori une version restreinte de SAT. En fait il n'en est rien car, comme nous allons le voir dans cette partie, toute instance de SAT peut être transformée en une instance de SAT (pour ) par un algorithme de complexité polynomiale. Ainsi, l'algorithme codé à la question 19, ou tout autre algorithme exponentiel optimisé pour -SAT, peut en fait résoudre n'importe quelle instance de SAT avec la même complexité.
Pour la transformation proprement dite, la première étape consiste à mettre en FNC la formule booléenne considérée. En effet, toute formule booléenne peut être mise en FNC et une approche évidente pour ce faire est d'utiliser les propriétés des connecteurs logiques rappelées dans la partie préliminaire.
Question 20 Pour chacune des formules suivantes, utiliser l'involutivité de la négation, l'associativité et la distributivité des connecteurs et , ainsi que les lois de De Morgan pour transformer la formule en FNC. Seul le résultat du calcul est demandé :
a)
b)
L'exemple b) de la question 20 se généralise à des formules de taille arbitraire, ce qui montre que l'approche ci-dessus n'est pas efficace puisque la FNC obtenue peut avoir une taille exponentielle en la taille de la formule booléenne de départ. Nous allons donc adopter une autre stratégie, qui sera d'introduire de nouvelles variables et de remplacer par une autre formule qui est équisatisfiable, c'est-à-dire que est satisfiable si et seulement si l'est. La formule sera en FNC et sa taille sera polynomiale en . La procédure pour construire à partir de fonctionne en deux temps :
  1. On commence par appliquer les lois de De Morgan récursivement à l'arbre d'expression associé à , de manière à faire descendre toutes les négations au niveau des nœuds parents des variables. Soit la nouvelle formule ainsi obtenue, qui par construction est logiquement équivalente à . Par exemple, si est la formule a) de la question 20, alors .
  2. Ensuite on applique récursivement les règles de réécriture suivantes à l'arbre d'expression de :
  • si , alors on pose , où et sont les versions réécrites de et respectivement,
  • si , alors on introduit une nouvelle variable booléenne dans la formule et on pose , où et sont les versions réécrites de et respectivement.
    Par exemple, en reprenant la formule obtenue dans l'exemple de l'étape 1 , on a en introduisant les nouvelles variables et .
Question 21 Montrer que les formules et sont équisatisfiables.
Question 22 Écrire une fonction negs_en_bas qui effectue l'étape 1 ci-dessus, c'est-à-dire qu'elle prend en argument une formule et renvoie une autre formule logiquement équivalente et dans laquelle tous les connecteurs ont des variables pour fils dans l'arbre d'expression. La fonction negs_en_bas doit avoir une complexité linéaire en la taille de .
negs_en_bas: formule -> formule
On se donne à présent une nouvelle fonction var_max, qui prend une formule en argument et qui renvoie le plus grand indice de variable utilisé dans la formule. La complexité de la fonction est linéaire en la taille de la formule.
Question 23 Écrire une fonction formule_vers_fnc qui prend en argument la formule obtenue à l'issue de l'étape 1 et qui renvoie la construite comme à l'étape 2 . La complexité de la fonction formule_vers_fnc doit être polynomiale en la taille de .
formule_vers_fnc: formule -> fnc
Question 24 Justifier les complexités des fonctions negs_en_bas et formule_vers_fnc. On pourra par exemple montrer que le nombre de clauses formées dans formule_vers_fnc est égal au nombre de littéraux dans la formule .
Ainsi, il suffit de combiner les fonctions des questions 22 et 23 pour convertir n'importe quelle formule booléenne en une FNC équisatisfiable en temps polynomial.
De manière similaire, on peut convertir la FNC en une 3-FNC équisatisfiable en temps polynomial. L'approche est la suivante : toute clause de avec au plus 3 littéraux reste inchangée, tandis que toute clause avec devient :
,
où sont de nouvelles variables introduites spécialement pour cette clause. On peut alors montrer que la formule ainsi obtenue est de taille polynomiale en la taille de et équisatifsiable. Dès lors, l'instance initiale de SAT est transformée en une instance de 3-SAT (et donc de -SAT pour n'importe quel ) équisatisfiable et de taille polynomiale.
La méthode décrite dans la partie IV du sujet transforme toute instance de SAT en une instance de 3-SAT équisatisfiable en temps polynomial. Dès lors, la fonction eval de la question 18 permet, étant données une formule booléenne quelconque de taille à variables et une valuation Vrai, Faux , de vérifier en temps polynomial (en , rappelons que l'on a ) si Vrai. Ainsi, du point de vue de la théorie de la complexité, le problème SAT se trouve être dans la classe de complexité NP. Cette classe est constituée précisément des problèmes dont on peut vérifier la solution en temps polynomial quand cette dernière existe. Cela ne veut pas dire qu'une telle solution peut être trouvée (ni même son existence déterminée) en temps polynomial. Les problèmes pour lesquels c'est le cas forment la classe de complexité appelée P . Clairement, on a puisque si l'on peut trouver une solution en temps polynomial alors on peut a fortiori vérifier en temps polynomial qu'on a bien une solution. Savoir si P est égal à NP est une question encore ouverte à ce jour et sans conteste l'une des plus fameuses en informatique fondamentale.
Parmi les problèmes de la classe NP, certains sont particulièrement difficiles, au moins aussi difficiles que tous les autres. Ces problèmes sont dits NP-complets. Formellement, un problème est dit NP-complet s'il existe une réduction polynomiale de chaque problème vers ce problème, c'est-à-dire un algorithme qui transforme toute instance de en une instance de en temps polynomial, de telle sorte que la réponse ("oui" / "non") de sur l'instance transformée est la même que celle de sur l'instance initiale . Un problème NP-complet permet ainsi de résoudre les instances de n'importe quel autre problème de la classe NP. D'où l'importance des problèmes NP-complets, puisque si l'un d'eux s'avérait
être dans P alors tous les autres y seraient également et l'on aurait . A contrario, si l'on avait alors aucun problème NP-complet ne serait résoluble en temps polynomial.
Historiquement, SAT fut le premier problème à être identifié comme étant NP-complet. C'est le fameux théorème de Cook-Levin (1971). Ce résultat explique l'importance qu'a eue SAT dans le développement de la théorie de la complexité. La transformation décrite dans la partie IV du sujet donne une réduction polynomiale de SAT à 3-SAT. Dès lors, 3-SAT (ainsi que -SAT pour tout est également NP-complet. Par conséquent, l'algorithme exponentiel de la question 19 permet de résoudre toutes les instances de tous les problèmes de la classe NP. A contrario, si alors il n'existe pas d'algorithme permettant de résoudre chacune des instances de 3 -SAT (ou de -SAT pour ) en temps polynomial. On comprend dès lors l'ampleur du fossé qui sépare les petites valeurs de , pour lesquelles des algorithmes linéaires existent comme décrit dans les parties I et II du sujet, des valeurs plus grandes ( ), pour lesquelles il n'existe peut-être pas d'algorithme polynomial. Ceci est l'un des nombreux effets de seuil observés dans la complexité du problème SAT et de ses variantes.
X ENS Option Informatique MP 2016 - Version Web LaTeX | WikiPrépa | WikiPrépa