Dans ce problème, on étudie diverses méthodes d'accélération d'ions positivement chargés par des champs électriques. On se place dans l'approximation des régimes quasi-stationnaires, et dans le cadre de la mécanique newtonienne. On donne :

Masse du proton
Charge élémentaire
Permittivité du vide
Perméabilité magnétique du vide

Première partie Accélérateur électrostatique

Des particules de masse et de charge sont accélérées par un champ électrique , supposé uniforme, régnant entre les deux armatures et d'un condensateur plan, distantes de , et de potentiels et . Le dispositif est représenté sur la figure 1 . On note la vitesse des particules au niveau de l'armature . Calculer leur vitesse au niveau de l'armature en fonction de et de la différence de potentiel entre les deux armatures.

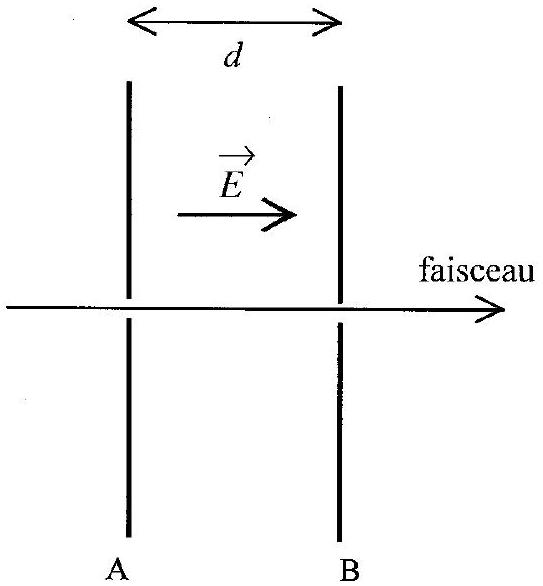
Figure 1

Application numérique : On suppose

négligeable devant

. Calculer

pour un proton, puis pour un ion césium

, dont la masse est approximativement 137 fois celle du proton. On donne

.
2. Le résultat précédent serait-il modifié pour une forme différente des armatures du condensateur?
3. On cherche à obtenir la tension continue

en redressant une tension alternative au moyen du dispositif représenté schématiquement sur la figure

représente une diode, supposée idéale, et le générateur délivre la tension

, de période

. A

, le condensateur n'est pas chargé.

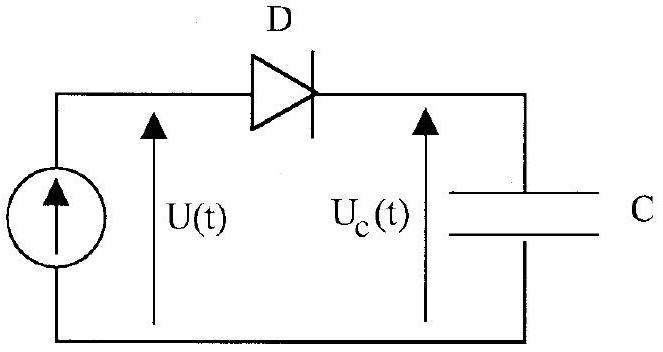
Figure 2

a) Calculer la tension aux bornes du condensateur

en fonction de

et représenter graphiquement sa variation.
b) Calculer la valeur maximale de la valeur absolue de la tension aux bornes de la diode.
4. Le dispositif précédent ne permet pas d'atteindre des tensions très élevées, car la diode claquerait. Pour l'améliorer, on utilise le dispositif représenté sur la figure 3 , où sont définies les charges

des armatures des condensateurs, les intensités

, ainsi que leurs conventions de signe. Les diodes

sont supposées idéales. Les condensateurs ne sont pas chargés à l'instant initial

, et la tension délivrée par le générateur vaut toujours

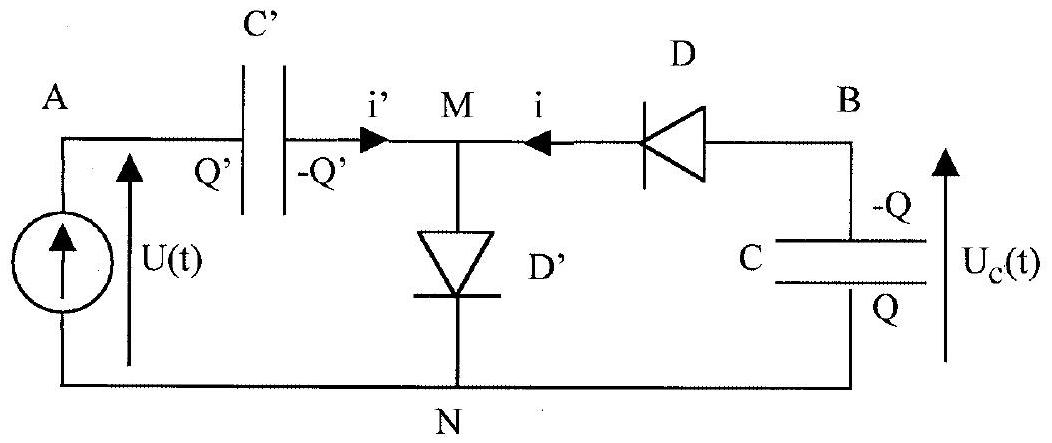
Figure 3

a) Relier

.
b) Montrer que

est une fonction croissante du temps.

est donc toujours positive.
c) On suppose la diode

passante. Relier alors

, et montrer que la diode

est nécessairement bloquée.
d) Montrer, en raisonnant par l'absurde, que lorsque

décroît,

est nécessairement bloquée, et que

est constante.
e) Montrer de même par l'absurde, et à l'aide des questions 4.b), 4.c), 4.d), que si

croît,

est bloquée, et que

reste constant.
5. On admet alors que la diode

devient passante avant que

n'atteigne son maximum

.
a) En déduire que la valeur maximale de

est

, et qu'elle est atteinte chaque fois que

atteint sa valeur maximale.
b) On note

les valeurs respectives de

lorsque

atteint pour la n

è

fois son minimum

. On admet que la diode

devient passante avant que

n'atteigne ce minimum. Relier

. En utilisant ce qui précède, montrer que

vérifie la relation de récurrence

c) La suite

converge-t-elle ? Déterminer la valeur asymptotique

de la charge aux bornes du condensateur

lorsque

. Que valent alors les tensions aux bornes de

et aux bornes de

?
d) Quelle est la valeur maximale de la tension aux bornes des diodes

lorsque

ont atteint leurs valeurs asymptotiques? Quel est donc l'intérêt de ce dispositif?

Deuxième partie

Accélération par une tension alternative

On peut également obtenir des accélérations importantes en utilisant directement le champ alternatif, sans avoir besoin de le redresser par des diodes, au moyen du dispositif représenté sur la figure 4, connu sous le nom d'appareil de Wideroë.

Figure 4

La tension

, est cette fois appliquée entre des tubes de glissement, boîtes complètement fermées, à l'exception de deux petits trous percés à leurs extrémités et permettant
de laisser passer le faisceau de particules. L'idée est d'accélérer les particules lorsqu'elles passent d'un tube à l'autre. Les tubes sont supposés parfaitement conducteurs.

Expliquer pourquoi on peut considérer l'accélération comme nulle à l'intérieur des tubes.
On note la longueur du tube la vitesse d'une particule à l'intérieur de ce tube, et l'instant auquel elle y entre. Expliquer qualitativement pourquoi on a intérêt à avoir (condition dite de synchronisme).
On appelle le potentiel au point où se trouve la particule à un instant . On note l'instant auquel la particule quitte le tube .
a) Exprimer la différence de potentiel à l'aide de , en distinguant selon la parité de .
b) On considère le temps de passage d'un tube à l'autre comme très petit devant la période , et l'on suppose réalisée la condition de synchronisme de la question 2. précédente. Montrer que dans ces conditions on a, pour tout , une différence de potentiel indépendante de : , où étant l'instant auquel la particule entre dans le tube . Quel est le rôle de la condition, que l'on supposera réalisée, ?
c) Relier et ; en déduire . Exprimer en fonction de et .
Application numérique :
a) Calculer la longueur du premier tube pour des ions , en prenant pour vitesse d'injection la valeur obtenue à la question 1. de la première partie, à la sortie du condensateur, pour une tension constante d'accélération . On donne .
b) On donne pour la machine de Wideroë . Pour quelle valeur de l'énergie de la particule aura-t-elle au moins doublé ? En déduire l'ordre de grandeur de la longueur totale de l'accélérateur pour atteindre une énergie double de l'énergie d'injection.
c) On injecte dans le dispositif précédent un ion de même charge et de même vitesse , mais de masse différente . Les valeurs des et sont les mêmes que précédemment, mais l'instant de l'injection peut différer de . On pose . À quelle condition sur existe-til une valeur de telle que la condition de synchronisme soit réalisée? Calculer numériquement le nombre de masse maximal que peut avoir un ion pour être accéléré de manière synchrone.
À paramètres donnés, la condition de synchronisme n'est réalisée que si la particule entre exactement à l'instant , à une période près. Etudier qualitativement l'accélération d'une particule entrant avec la même vitesse , mais légèrement en retard, à un instant un peu postérieur à . Aura-t-elle tendance à combler son retard? On discutera suivant la valeur de . On étudiera de même le cas d'une particule arrivant légèrement en avance. Que peut-on en conclure quant à la stabilité du mécanisme de synchronisme ? Si l'on injecte à l'entrée de l'appareil un faisceau continu, qu'observera-t-on, qualitativement, à la sortie?
On va maintenant étudier de façon plus quantitative la stabilité du mécanisme d'accélération, dans le cas où l'augmentation de vitesse dans l'accélérateur est très petite devant la vitesse initiale , c'est-à-dire .
a) On note toujours la vitesse de la particule synchrone lorsqu'elle traverse le tube , calculée dans la question 3.c) de cette partie. Exprimer au premier ordre dans le potentiel accélérateur . On supposera très peu différente de .
b) On considère maintenant une particule non synchrone, de même masse, et injectée exactement avec la même vitesse , mais à un instant un peu différent . On notera l'instant où elle entre dans le tube sa vitesse dans ce tube, avec par hypothèse . On pose . Que vaudrait si la particule était synchrone ( pour tout )?

Calculer la variation de vitesse entre deux tubes,

, au premier ordre en

, et en fonction de

.
c) On pose

, où

désigne la vitesse de la particule synchrone, avec par hypothèse

. En utilisant les résultats des questions

) et

) précédentes, en déduire que

d) En traitant

comme un infiniment petit du premier ordre, c'est-à-dire tel que

, établir la relation cinématique

e) Les variations de la vitesse

et de la phase

étant faibles d'un tube à l'autre, on peut traiter

comme un paramètre continu et noter indifféremment

, et

. On pose alors

. Écrire l'équation différentielle du second ordre vérifiée par

. Quelles sont les conditions initiales sur

?
f) Montrer que l'équation différentielle vérifiée par

est formellement analogue à l'équation du mouvement d'un point matériel se déplaçant sur un axe

réel, dans une énergie potentielle

dont on donnera l'expression. On prend

. Quels sont les extrema de

? Tracer son graphe pour

.
g) Montrer comment on peut déterminer graphiquement le domaine de valeurs initiales

pour lesquelles on observe des oscillations de

autour de la phase synchrone

Troisième partie

Accélération dans un circuit résonant

Pour obtenir des vitesses plus élevées au moyen du dispositif précédent, il faut des champs de fréquence plus grande, ce qui conduit à utiliser un dispositif un peu différent, utilisant un circuit résonant (« linac» d'Alvarez). Les applications numériques de cette partie utilisent
des paramètres voisins de ceux du linac pré-injecteur du synchrotron à protons de Brookhaven (USA).

Comme précédemment, le dispositif est composé d'éléments mis bout à bout. Il admet une symétrie de révolution autour de l'axe du faisceau,

. Un élément est représenté sur la figure 5, en coupe suivant un plan

. Le faisceau passe dans des tubes de glissement conducteurs de rayon

dont les extrémités sont fermées par des disques percés en leur centre ; il est accéléré dans l'intervalle

entre deux tubes consécutifs. Les tubes sont insérés dans un cylindre conducteur de rayon

et de longueur

, auquel ils sont reliés par des fils conducteurs. Un courant

peut alors circuler, qu'on supposera dirigé suivant l'axe

et réparti uniformément sur la surface du cylindre extérieur d'une part, et, en sens inverse, sur celle des tubes intérieurs d'autre part.

On admettra que le champ magnétique créé par le courant circulant dans les fils reliant le cylindre extérieur aux tubes de glissement peut être négligé, car les courants correspondant à deux éléments successifs s'annulent mutuellement. Seules contribuent alors au champ magnétique les nappes de courant circulant sur le cylindre extérieur et sur les tubes. On négligera également, pour ce calcul, l'espace

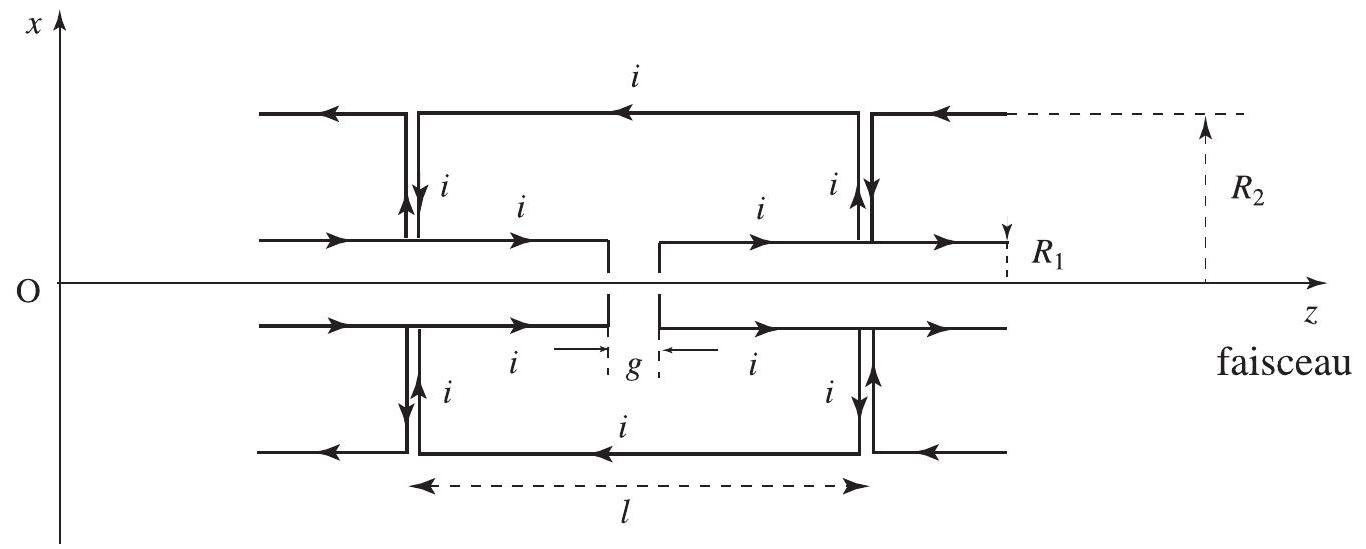
entre les tubes. Le système peut donc être assimilé à un ensemble de deux cylindres coaxiaux.

Figure 5

Déterminer la direction du champ magnétique dans tout l'espace en utilisant un argument de symétrie clairement explicité.
Calculer le champ dans la cavité délimitée par le cylindre et les tubes, en fonction de la distance à l'axe du faisceau et de l'intensité totale .
Calculer l'énergie magnétique contenue dans un élément de longueur du système. En déduire l'inductance de cet élément.

Application numérique : Calculer

pour

.
4. Calculer la capacité

du condensateur plan constitué par les extrémités des deux tubes de glissement, en supposant

. Dans le problème, on néglige la capacité des conducteurs cylindriques emboîtés.

Application numérique : Calculer

pour

en adoptant l'expression obtenue.
5. Calculer, littéralement puis numériquement, la fréquence de résonance

du circuit constitué par cette inductance et cette capacité.
6. Calculer la longueur d'onde

associée. L'approximation des régimes quasi-stationnaires vous paraît-elle justifiée ici?
7. Le circuit n'est en fait pas idéal, et il existe des pertes par effet Joule, dont on notera

la puissance moyenne pour l'élément étudié ci-dessus. On rappelle la définition du facteur de qualité

est égal au rapport de l'énergie totale emmagasinée dans le circuit et de l'énergie dissipée pendant une période, ces quantités étant calculées à la résonance. Calculer le facteur de qualité

du circuit en fonction de

, tension maximale aux bornes du condensateur.

Application numérique : Calculer

pour

.
8. Si l'on accole plusieurs éléments tels que celui représenté sur la figure 5 , on remarque que les potentiels à la sortie de deux tubes consécutifs vibrent en phase. À quelle condition une particule accélérée dans cette structure verra-t-elle toujours le même potentiel à la sortie de chaque tube (condition de synchronisme) ?

Application numérique : Calculer la vitesse que doit avoir une particule traversant l'élément considéré plus haut pour que la condition de synchronisme soit réalisée. L'utilisation de la mécanique newtonienne est-elle toujours justifiée?

Rapport de MM. P. KIERLIK et B. MOSSER, correcteurs.

Le problème portait sur l'étude de diverses méthodes d'accélération d'ions par des champs électriques. Il était constitué de trois parties pratiquement indépendantes les unes des autres. La première partie traitait principalement d'un dispositif à diodes permettant l'obtention sans claquage des diodes de tensions continues élevées (« pompe à diodes »). Elle a été abordée par les candidats avec des succès très divers. Les connaissances requises étaient minimales (lois des circuits, caractéristique d'une diode) mais un grand nombre de candidats n'ont pas su maîtriser les raisonnements par l'absurde, parfois délicats, du milieu de cette partie. La deuxième partie décrivait l'accélérateur de Wideroë et proposait une étude de sa stabilité. Il convenait d'avoir compris comment le dispositif fonctionnait dans son ensemble : ce ne fut hélas pas le cas pour la majorité des candidats qui se contentèrent souvent de mener les calculs les plus simples. Enfin la troisième partie étudiait quelques ordres de grandeurs des performances d'un autre accélérateur (« Linac » d'Alvarez). Les questions étaient élémentaires et testaient les connaissances de base du candidat en magnétostatique, électrostatique et circuit résonnant. Elle n'a pu être abordée, faute de temps que par environ la moitié des candidats. Si l'épreuve était donc plutôt longue, notons cependant qu'un petit nombre de candidats a entièrement traité le problème.

La moyenne des 1295 candidats français s'est établie à 10,1 avec un écart type de 3,8 . La répartition des notes est la suivante avec

de notes éliminatoires (note

) :

Rappelons, comme chaque année, les règles générales que nous adoptons pour l'établissement du barème :

il s'agit avant tout d'une épreuve de physique. Les candidats en saisissent-ils toutes les implications? Application numérique avec une unité, analyse critique des résultats les plus significatifs, justification des relations employées, bon sens « physique » sont autant de points fondamentaux qui doivent rester présents à l'esprit du candidat.
toutes les questions sont notées, y compris les plus triviales. Il est tout à fait étonnant de constater que nombre de candidats oublient ou négligent de répondre à la totalité de qui leur est demandé.
les raisonnements qualitatifs peuvent et doivent avoir la même rigueur et la même clarté que les calculs analytiques. Le charabia, les idées contradictoires d'une ligne à l'autre ou l'ambiguïté permanente sont sévèrement sanctionnés. A contrario, une analyse physique bien menée est toujours récompensée.
un schéma clair vaut aussi bien qu'un discours et peut contenir des éléments tout aussi précieux et essentiels (orientation d'un contour, choix des conventions dans un circuit).
enfin, rappelons qu'une écriture lisible et l'aisance dans l'expression sont jugés favorablement par les correcteurs.

Première partie

A notre grand surprise, beaucoup de candidats ont préféré une approche mécanique (à partir de la relation fondamentale de la dynamique) à une approche énergétique (théorème de l'énergie cinétique) Un laborieux calcul s'ensuivait . . . Trop de candidats se sont abstenus d'effectuer les deux applications numériques demandées (pour le proton et pour le césium).
Question bien mal traitée, surtout par les partisans de l'approche mécanique. Peu de copies interprètent correctement le résultat de l'approche énergétique (le champ de force électrostatique est à circulation conservative), encore moins que la surface d'un conducteur parfait à l'équilibre est une équipotentielle.
Que n'a-t-on vu comme redressements simple alternance ou comme spectaculaires discontinuités de tension aux bornes du condensateur dans cette question!
4.a Quelques candidats oublient que la relation entre charge et intensité relève de la convention de signe choisie. L'état des diodes n'influait en rien sur le résultat.
4.c Des erreurs de signe et des réponses bien alambiquées pour justifier le blocage de .
4.d, 4.e Ces questions étaient délicates : elles nécessitaient plusieurs étapes, en soit simples mais dont la succession logique a conduit beaucoup de candidats à l'erreur. Pour la question 4.d, beaucoup de candidats n'ont pas convenablement justifié que était bloquée si l'on supposait que était passante.
5.b Question plutôt bien traitée par ceux qui l'ont abordée. Cependant, rappelons aux candidats que les copies sont lues avec attention. Il est particulièrement désagréable pour le correcteur de s'apercevoir que partant d'une(ou plus) relation(s) fausse(s), le candidat obtient néanmoins la formule désirée : la cohérence dans les calculs est préférable à de douteuses manipulations, quitte à ce que le candidat signale dans sa copie le désaccord constaté.
5.c Bien entendu, il était possible de sortir tout un arsenal mathématique pour justifier la convergence de la suite (fonction lipschitzienne contractante, suite arithméticogéométrique). Mais le physicien apprécie les arguments physiques qui expliquent pourquoi la charge et la tension ne peuvent atteindre des valeurs infinies. Par ailleurs, cela évite d'en passer par le calcul direct de , dont force est de constater qu'il est hors de portée
de nombre de candidats.
5.d L'intérêt du dispositif a échappé à presque tous.

Deuxième partie

Beaucoup de confusion entre l'intérieur d'un conducteur parfait et une cavité au sein d'un conducteur parfait. Peu de candidats font l'analogie avec la cage de Faraday.
Cette question cruciale a été fort mal traitée. Curieusement, ce n'est pas dans les meilleures copies que l'on trouve les discussions les plus intéressantes. Une majorité des candidats ne semble pas s'être aperçu du caractère essentiel de l'alternance des branchements entre tubes successifs.
3.a, 3.b Il fallait pour résoudre ces questions poser une référence de potentiel, le plus simple étant de considérer que les tubes pairs étaient reliés à la masse. Pour n'avoir pas distingué potentiel et différence de potentiel, la plupart des candidats se sont fourvoyés.
4.a, 4.b Ces applications numériques ont bien trop souvent été négligées et sont toujours aussi peu commentées. Beaucoup d'erreurs numériques pas très flagrantes (un facteur 10 ou 100) à cause d'erreurs de conversion dans les puissance de dix.
4.c Des calculs analytiques justes sont souvent gâchés par des applications numériques plus hasardeuses.
Cette question était purement qualitative et pouvait nécessiter un assez long développement. Entre les candidats qui semblent ignorer que la fonction sinus est croissante entre 0 et , ceux qui ne travaillent que par ébauche, ceux qui mènent brillamment un raisonnement mais qui concluent de travers, peu finalement ont donné des réponses complètes et satisfaisantes. Les correcteurs leur en surent gré.
6.b Cette question ne pouvait être traitée que si le candidat avait répondu correctement aux questions 3.a et 3.b. Comme cela n'était pas souvent le cas, les correcteurs ont eu le droit à des calculs sans réelle justification et donc sans valeur.
6.d Question peu souvent traitée.
6.e, 6.f, 6.g Curieusement, alors que les préalables à ces questions figuraient explicitement aux questions 6.c et 6.d, les candidats ont raté ces questions. Même ceux qui ont trouvé l'équation différentielle correcte sur n'ont pas su la plupart du temps profiter de l'analogie mécanique proposée. L'obtention de l'énergie potentielle à partir de la force a donné lieu à maintes erreurs de signe ou d'intégration, qui rendaient la suite caduque. Seule une poignée de candidats a achevé cette partie.

Troisième partie

L'argument de symétrie n'a pas toujours été bien explicité : pour déterminer la direction du champ en un point, il faut exhiber des éléments de symétrie qui passent par ce même point.
L'utilisation du théorème d'Ampère n'est justifiée que parce que le problème se traite dans l'approximation des régimes quasi-stationnaires, ce qu'ont oublié presque tous les candidats. Beaucoup d'erreurs dans ce calcul pourtant élémentaire du champ magnétique.
Si peu de candidats ignorent la définition énergétique de l'inductance propre d'un circuit, un certain nombre ont obtenu des expression fausses de l'énergie magnétique, faute d'intégrer convenablement une fonction radiale dans une géométrie cylindrique.
Le condensateur plan reste difficile à appréhender pour la plupart des candidats, ce qui a valu aux correcteurs de laborieux calculs. Peu de candidats ont remarqué que l'hypothèse d'un condensateur plan n'était pas vraiment vérifiée.
5., 6. Réponses littérales exactes, mais les applications numériques, conditionnées par les résultats des questions précédentes étaient très souvent incorrectes.
Question très mal traitée parce que les candidats n'ont pas su exprimer l'énergie emmagasinée dans un circuit ou le lien entre puissance dissipée et énergie dissipée par période. Cela a conduit à des valeurs du facteur de qualité des plus farfelues!