L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.
On attachera une grande importance à la clarté, à la précision et à la concision de la rédaction.

Routage dans un réseau arborescent

Dans ce problème on aborde une question soulevée dans la conception des réseaux : il s'agit d'affecter des adresses distinctes aux nœuds d'un réseau de façon telle que la route entre deux nœuds puisse être déterminée par un calcul utilisant uniquement leurs deux adresses, sans référence à une connaissance globale du réseau. On s'intéresse plus particulièrement aux réseaux ayant une forme d'arbre.

Le problème est composé de trois parties indépendantes.

Dans tout le problème un

-arbre est un arbre dont l'ensemble des sommets (on dit aussi parfois les nœuds) est

, et dont la racine est 0 . Chaque sommet

possède un père noté pere

, par convention la racine est son propre père, ainsi pere

. L'ensemble des

-arbres est noté

L'ensemble des ancêtres du sommet

est constitué de

et des ancêtres de son père pere

; la racine 0 est ainsi ancêtre de tous les sommets de l'arbre. Le sous-arbre de racine a, noté

, est formé de tous les sommets de l'arbre

dont

est ancêtre.

Les fils d'un sommet

sont ainsi les

tels que pere

, (attention la racine n'est pas fils d'elle même). Une feuille est un sommet qui n'a pas de fils.

La hauteur (on dit aussi parfois profondeur) d'un sommet

, notée

est un entier égal à 0 si

est la racine, elle est égale à la hauteur du père de

augmentée de 1 sinon. Le plus proche ancêtre commun à deux sommets

, noté

, est le sommet de hauteur maximale qui est à la fois ancêtre de

et de

. Noter que si

est ancêtre de

alors

Dans tout le problème, on considère que l'entier

est fixé, d'autre part pour un tableau

dénote l'élément d'indice i ; une liste contenant les entiers

est représentée par

; la liste vide est notée

On utilisera pour un

-arbre

Un tableau de listes d'entiers fils de taille tel que fils[i] est la liste des fils de .
Un tableau d'entiers pere de taille tel que pere[i] est le père de .

On a ainsi en Caml et en Pascal

let n = ...;; const n = ...;
    type vint = array[0..n-1] of integer ;
type vint == int vect ;; lint = ^cellule;
type lint == int list ;; cellule = record
type vlint == lint vect ;; val : integer; suiv : lint;
    end;
    vlint = array[0..n-1] of lint;

On pourra utiliser en Pascal le constructeur pour les listes qui est donné ci-dessous :

function cons (contenu : integer; suivant : lint) : lint;
    begin
    var res : lint;
    new(res); res^.val := contenu; res`.suiv := suivant;
    cons := res;
end;

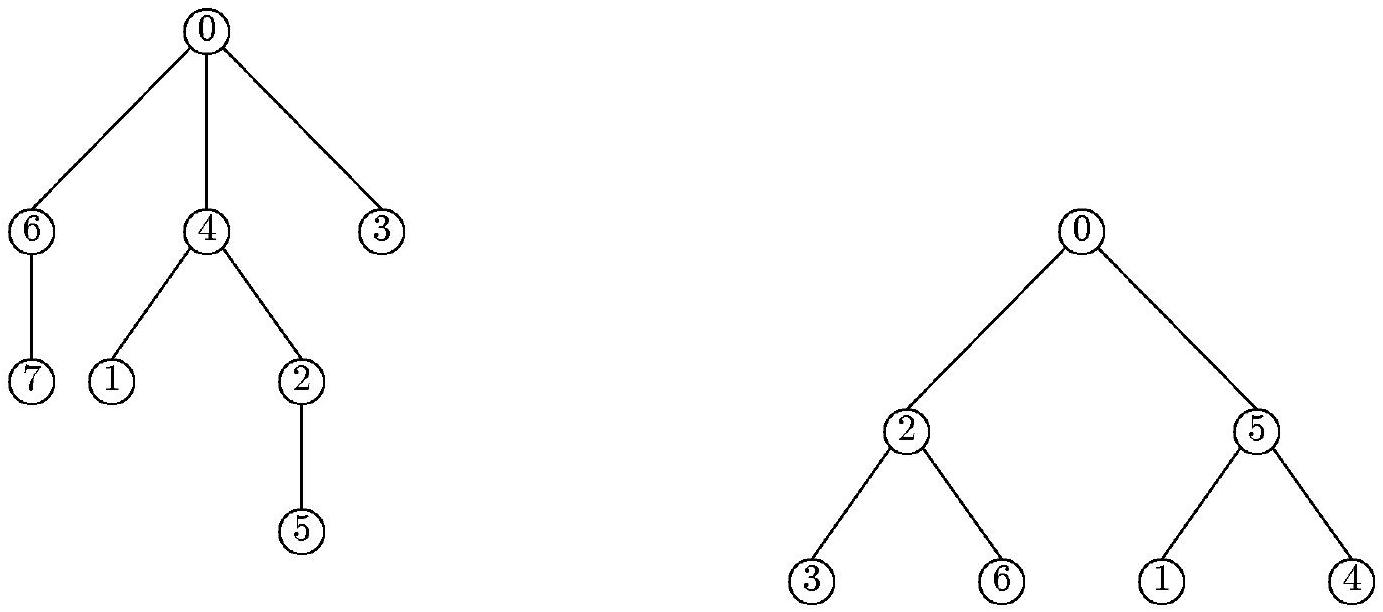
Fig. 1: Un arbre

et un arbre binaire complet

Les tableaux pere et fils de l'arbre

situé à gauche de la Figure 1 sont donnés par :

	0	1	2	3	4	5	6	7
pere	0	4	4	0	0	2	0	6
fils

I. Fonctions Élémentaires

Question 1. Calculer ppac

pour tous les couples de sommets de l'arbre

donné plus haut. On présentera le résultat sous forme d'un tableau de 8 lignes et 8 colonnes tel que la case sur la ligne

et la colonne

contienne le plus proche ancêtre de

Question 2. Écrire une fonction

hauteur : vint -> int -> int
function hauteur (pere : vint; a : integer) : integer

qui étant donné un sommet a d'un arbre, pour lequel on donne son tableau des pères, calcule la hauteur de ce sommet.

Question 3. Écrire une fonction

filsEnPere : vlint -> vint
procedure filsEnPere (fils : vlint; var pere : vint)

qui à partir d'un arbre, donné par ses listes de fils, calcule le tableau des pères.
Question 4. Écrire une fonction

ppacMemeH : vint -> int -> int -> int
function ppacMemeH (pere: vint; a, b: integer) : integer

qui calcule le plus proche ancêtre commun de deux sommets a et b supposés de même hauteur dans un arbre pour lequel on donne le tableau des pères.

En déduire une fonction ppac qui effectue le même calcul pour deux sommets a et b n'ayant pas nécessairement la même hauteur.

II. Arbres binaires complets

Un arbre binaire complet est un arbre dans lequel tout sommet qui n'est pas une feuille a exactement deux fils, et tel que toutes les feuilles sont à la même hauteur. On note

l'ensemble des

-arbres binaires complets dans lesquels les feuilles sont à hauteur

. Un exemple d'arbre binaire complet

est donné à droite de la Figure 1 .

Question 5. Déterminer pour

le nombre

de sommets de hauteur

dans un arbre

, justifiez votre réponse. En déduire le nombre

de sommets d'un arbre de

en fonction de

Dans la suite

est un arbre de

ayant

sommets ; à chaque sommet

on associe une étiquette

satisfaisant la condition suivante :
pour chaque sommet

ayant pour liste de fils

Question 6. Calculer les valeurs de

pour les 7 sommets de l'arbre binaire complet représenté sur la droite de la Figure 1 : l'ordre des fils dans les listes correspond à la lecture de gauche à droite de la figure.

Question 7. Écrire une fonction
etiquettes : vlint -> vint
procedure etiquettes (fils : vlint; var etiq : vint)
qui calcule les étiquettes

pour tous les sommets d'un arbre de

donné par ses listes de fils.

Question 8. Un arbre

de racine 0 ayant pour liste de fils

se décompose en deux sous-arbres

. Déterminer les valeurs de

, de

et de

pour les fils

de la racine.

Question 9. Démontrer que si

sont deux sommets quelconques de

alors

est déterminé de manière unique à partir de

par la propriété suivante :

est parmi les entiers compris (au sens large) entre

celui possédant le plus grand diviseur qui soit une puissance de 2 .

Question 10. Donner une fonction récursive
mu : int -> int -> int
function mu (p, q : integer) : integer
qui détermine

à partir de

; on supposera que

. Votre fonction doit être de complexité

III. Arbres généraux

Dans cette partie on utilise les définitions et notations suivantes:

Dans un arbre

le poids

d'un sommet

est le nombre de sommets du sous-arbre

de racine

, ainsi

si et seulement si

est une feuille, noter que

(c'est le nombre de sommets
de

Un arbre

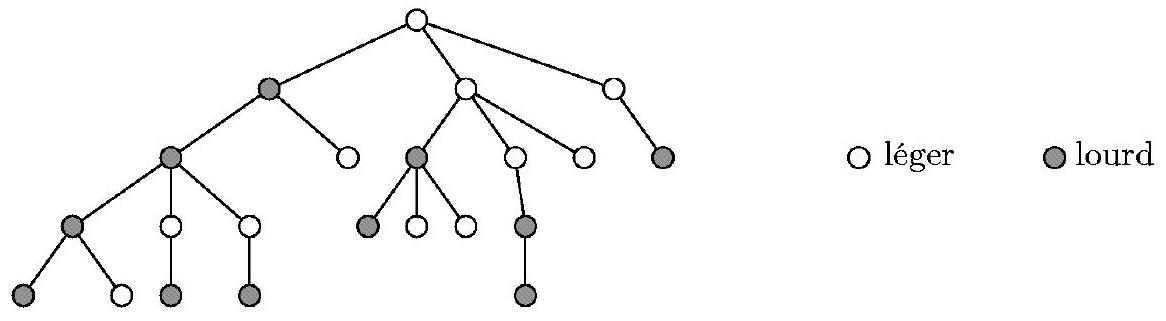
est dit gauche si pour chaque sommet

(qui n'est pas une feuille) le premier élément de la liste des fils est de poids supérieur ou égal à celui de tous les autres sommets de cette liste. Dans un arbre gauche, le premier élément de la liste des fils d'un sommet est dit lourd, les autres sommets sont dits légers. La racine est un sommet léger.

Fig. 2: Sommets lourds et légers.

Question 11. Écrire une fonction

poids : vlint -> vint
procedure poids(fils : vlint; var poids : vint)

qui calcule les poids de tous les sommets d'un arbre donné par ses listes de fils. Puis une fonction :

gauchir : vlint -> vint -> vlint
procedure gauchir (fils : vlint; w : vint; var filsG : vlint)

qui calcule un arbre gauche obtenu en réordonnant les fils de chaque sommet de façon telle que le premier fils soit de poids supérieur ou égal à celui des autres. Sont donnés dans cette fonction les listes des fils et le tableau des poids des sommets de l'arbre.

Question 12. Soit

un sommet léger d'un arbre gauche

son père, montrer que

. En déduire que le nombre d'ancêtres légers de

est inférieur à

On utilise dans toute la suite la notion de cime d'un sommet.

Si est léger cime est égale à pere .
Si est lourd cime est le plus proche ancêtre de qui est léger.

Ainsi en raison de nos conventions cime

. On appelle

l'arbre gauche obtenu en appliquant la fonction gauchir à l'arbre

de la figure 1 . Les cimes des sommets de l'arbre

sont alors données par le tableau suivant :

	0	1	2	3	4	5	6	7
cime	0	4	0	0	0	0	0	6

Question 13. Écrire une fonction

cimes : vlint -> vint
procedure cimes (fils : vlint; var cime : vint)

qui calcule les sommets cimes de tous les sommets à partir des listes de fils d'un arbre gauche.

On se propose d'attribuer des étiquettes aux sommets d'un arbre gauche

. Pour cela on commence par construire deux tableaux d'entiers

associés aux sommets. Le tableau

est tel que

est le

-ème élément de la liste des fils de son père.

Le tableau

est tel que

est léger et

pere

est lourd.

Les étiquettes

des sommets sont alors des listes d'entiers construites de la façon suivante:

dans cette formule o dénote la concaténation des listes.

Question 14. Donner l'arbre

défini à la question 12 ; puis donner les valeurs de

pour tous les sommets

; calculer enfin leurs étiquettes

Question 15. Écrire une fonction

etiquettes : vlint -> vint -> vlint
procedure etiquettes (fils : vlint; cime : vint; var lambda : vlint)

qui calcule les étiquettes des sommets d'un arbre gauche donné par ses listes de fils et pour lequel on donne aussi le tableau des cimes des sommets.

En Caml on pourra utiliser l'opérateur @ et en Pascal la fonction :

function concat (x, y : lint): lint;

qui calcule la concaténation de deux listes et dont on ne demande pas le corps.

Question 16. Écrire une fonction:

trouve : vlint -> lint -> int
function trouveSommet(fils : vlint; etiq : lint): integer

qui, à partir de l'étiquette d'un sommet d'un arbre gauche

et des listes de fils des sommets de cet arbre, détermine ce sommet.

Question 17.

a) Montrer que, pour tout sommet

d'un arbre, la longueur de l'étiquette

est majorée par 4 fois le nombre de ses ancêtres légers.
b) Indiquer comment on calcule

à partir des deux listes

; on ne demande pas de justifier la réponse à cette question.

On a donné dans ce problème une technique permettant d'étiqueter les nœuds des sommets d'un réseau qui a une forme d'arbre. Dans cet étiquetage la recherche du plus proche ancêtre commun de deux sommets (et donc de la route qui les relie) s'effectue uniquement à l'aide de leurs étiquettes. Des techniques plus complexes, qui généralisent les techniques données ici, utilisent des étiquettes de taille

bits qui permettent aussi un calcul du plus proche ancêtre commun en

opérations.

Dans tout l'énoncé du problème les déclarations de fonctions et procédures sont proposées d'abord en Caml puis en Pascal.