L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
On attachera une grande importance à la concision, à la clarté, et à la précision de la rédaction.

Codage Reed-Solomon

Ce problème s'intéresse aux codes de correction d'erreurs de Reed-Solomon. On souhaite transmettre un message au travers d'un canal de communication bruité : les données émises sont modifiées par quelques erreurs lorsqu'elles sont reçues. Pour permettre néanmoins la transmission fiable d'un message, la donnée émise est un codage du message, plus long que le message lui-même. La redondance ainsi ajoutée permet de corriger ensuite des erreurs qui peuvent apparaître lors de la transmission. Les codes appelés codes de Reed-Solomon ont de nombreuses applications : les CDs, DVDs, les systèmes ADSL, ou encore de nombreuses sondes spatiales utilisent des codes bâtis autour des codes de Reed-Solomon.

Le préambule donne les définitions communes à l'ensemble de l'énoncé, et introduit les codes de Reed-Solomon. La partie I s'attache au calcul du codage d'un message. La partie II définit quelques fonctions de manipulation de polynômes. La partie III poursuit cette étude par la mise en œuvre d'algorithmes de meilleure complexité. Enfin, la partie IV permet d'améliorer la complexité du codage. On notera que le problème du décodage (retrouver un message original à partir d'une transmission bruitée) n'est pas traité dans ce problème.

Les parties I à III peuvent être traitées indépendamment. La partie IV repose sur les résultats de la partie III.

Préambule : Définitions et notations

Dans l'ensemble de l'énoncé, on fixe un nombre premier

inférieur à

(de telle sorte que le produit de deux entiers modulo

soit toujours représentable par un simple entier positif en Caml ou en Pascal). Les calculs liés aux codes de Reed-Solomon seront réalisés dans le corps

des entiers modulo

. On rappelle que l'opération «modulo » est réalisée par l'opérateur mod en Caml et en Pascal, où on suppose également disposer de la fonction inv suivante pour calculer l'inverse modulo

de tout entier

vérifiant

é

    { Pascal }
(donné) function inv(a:integer)
    : integer

Toutes les questions ayant trait à la complexité des programmes écrits demandent comme réponse une borne supérieure (raisonnable) du type

sur le nombre d'opérations dans

: chacune des opérations dans

(addition, multiplication, inversion) est considérée de complexité 1 .

On manipulera des listes d'entiers modulo

en les identifiant avec des polynômes. Ainsi la liste de

entiers

correspond au polynôme

de degré inférieur ou égal à

, à coefficients dans

. On notera couramment deg

le degré d'un polynôme

. Les listes d'entiers modulo

sont des valeurs du type poly, défini comme suit :

    (* Caml *)
type poly = int list;;

        { Pascal }
type poly = `polycoeff;
polycoeff = record
    coeff: integer;
    suivant: poly;
end;

En Pascal la liste vide est nil, et l'on pourra utiliser la fonction suivante pour construire des listes:

    { Pascal }
function nouveauPolynome(a : integer ; Q : poly) : poly;
var r : poly;
begin new(r); r^.coeff := a ; r^.suivant := Q; nouveauPolynome := r; end;

Pour définir le codage de Reed-Solomon, on fixe deux constantes entières

qui vérifient

Le codage de Reed-Solomon transforme un message en un codage. Le message est une liste

entiers modulo

, tandis que le codage est une liste

entiers modulo

. On peut aussi voir le message comme un polynôme

de degré inférieur ou égal à

. Le codage utilise comme paramètre une liste

entiers modulo

, et est calculé comme suit :

Dans les programmes qu'on écrira, on considérera les entiers

comme des constantes globales.

Partie I. Codage de Reed-Solomon, première version

Question 1 Écrire la fonction valeur qui prend comme arguments un polynôme

à coefficients dans

et un entier

; et qui retourne la valeur

dans

de ce polynôme en cet entier

(* Caml *) valeur : poly -> int -> int
{ Pascal } function valeur(U : poly ; x : integer) : integer

Question 2 Écrire la fonction codage qui prend comme arguments la liste

et le polynôme

; et qui retourne le codage de Reed-Solomon du message

(* Caml *) codage : poly -> poly -> poly
{ Pascal } function codage(\alpha : poly ; A : poly) : poly

Question 3 Quelles sont les complexités des fonctions valeur et codage en fonction de

Partie II. Polynômes

Dans cette partie, toutes les opérations retournent des polynômes à coefficients dans

Question 4 Écrire la fonction addition qui prend comme arguments deux polynômes

à coefficients dans

, représentés par des listes de

coefficients; et qui retourne la somme de ces deux polynômes. Les coefficients du résultat sont aussi dans

. Déterminer la complexité de cette fonction en fonction de

(* Caml *) addition : poly -> poly -> poly
{ Pascal } function addition( U : poly ; V : poly) : poly

Question 5 Écrire de même la fonction soustraction qui prend comme arguments deux polynômes

à coefficients dans

, représentés par des listes de

coefficients; et qui retourne la différence

. Déterminer la complexité de cette fonction en fonction de

(* Caml *) soustraction : poly -> poly -> poly
{ Pascal } function soustraction( U : poly ; V : poly) : poly

Question 6 Écrire la fonction produitParScalaire qui prend comme arguments un polynôme

, représenté par la liste de

coefficients, et un entier

dans

; et qui retourne

. Donner la complexité de cette fonction en fonction de

(* Caml *) produitParScalaire : poly -> int -> poly
{ Pascal } function produitParScalaire(U : poly ; s : integer) : poly

Question 7 Écrire la fonction produit qui prend comme arguments deux polynômes

, représentés par des listes de

coefficients; et qui retourne le produit de ces deux polynômes. Déterminer la complexité de cette fonction en fonction de

(* Caml *) produit : poly -> poly -> poly
{ Pascal } function produit( U : poly ; V : poly) : poly

Question 8 Soit un polynôme

de degré inférieur ou égal à

représenté par une liste de

entiers, et un polynôme non nul

de degré exactement égal à

, représenté par une liste de

entiers. Écrire la fonction division qui calcule le quotient de la division euclidienne de

par

, noté

. On rappelle que le résultat de la division euclidienne d'un polynôme

par un polynôme non nul

est l'unique couple (

) (quotient et reste) vérifiant :

Déterminer la complexité de la fonction division en fonction de

.
(* Caml *) division : poly -> poly -> poly
{ Pascal } function division (

: poly ;

: poly) : poly

Question 9 Écrire la fonction modulo qui prend comme arguments deux polynômes

; et qui calcule le reste de la division euclidienne de

par

. Quelle est la complexité de cette fonction?
(* Caml *) modulo : poly -> poly -> poly
{ Pascal } function modulo (

: poly ;

: poly) : poly

Dans la suite du problème, le reste de la division euclidienne de

par

est noté

Partie III. Multiplication et division rapide

Cette partie s'attache à l'amélioration de la complexité des algorithmes de multiplication et de division de polynômes. La notation

(respectivement

) désigne la partie entière inférieure (respectivement la partie entière supérieure) d'un nombre réel

. On remarque qu'on a, pour tout nombre entier

, l'équation

Multiplication Soient deux polynômes

représentés par les listes

ayant

coefficients (le degré de

est donc au plus

). On pose

puis

, de sorte que

. On définit de même

. Lorsqu'on écrit le produit

, on fait apparaître quatre produits impliquant les polynômes

Question 10 Donner une formule par laquelle le produit

s'exprime sous la forme

, où les polynômes

se calculent avec seulement trois produits impliquant les polynômes

Question 11 Écrire la fonction produitRapide qui prend comme arguments deux polynômes

représentés par des listes de

coefficients; et qui calcule leur produit, avec une complexité

dans le cas où

est une puissance de 2 . Justifier cette formule de complexité.

(* Caml *) produitRapide : poly -> poly -> poly
{ Pascal } function produitRapide( }U : poly ; V : poly) : poly

Division Il est possible d'obtenir une amélioration similaire de la division de polynômes. Soit un dividende

et un diviseur non nul

, respectivement représentés par les listes

d'entiers. On suppose que

est non nul, de telle sorte que deg

est exactement égal à

. Le degré de

est au plus égal à

Comme pour la multiplication, on sépare les entrées en « partie haute » et « partie basse ». On pose

, puis

. Le découpage est représenté par la figure 1. Attention, selon la parité de

, on a

On recherche le quotient

, écrit sous la forme

avec

. Les formules suivantes donnent la valeur de

est le quotient de la division de par .
est le reste de cette même division.
est le quotient de la division de par , où :

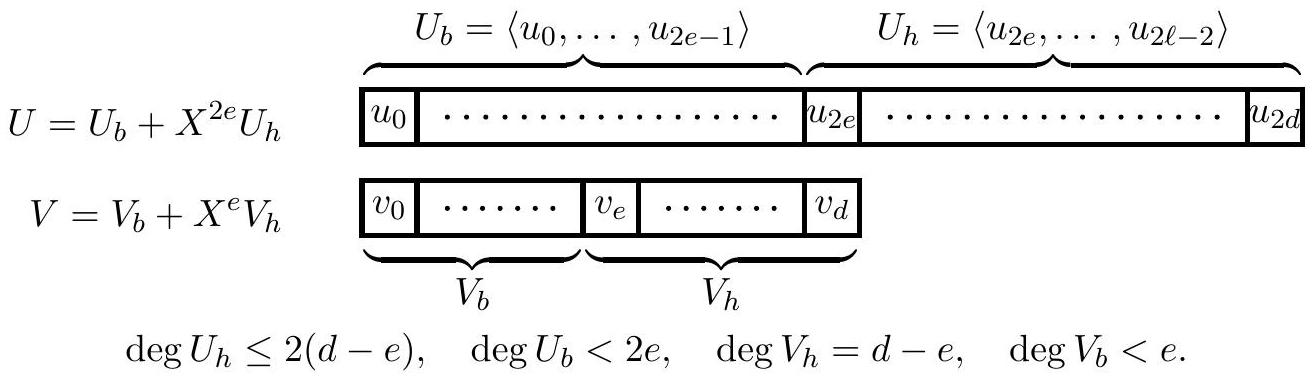
Fig. 1: Découpage de

pour divisionRapide, où

Question 12 Écrire la fonction divisionRapide qui prend comme arguments deux polynômes

représentés comme dans ce qui précède par deux listes de

coefficients, avec

non nul ; et qui calcule leur quotient en utilisant cet algorithme. Quelle est la complexité de cette fonction dans le cas où

est une puissance de deux?

(* Caml *) divisionRapide : poly -> poly -> poly
{ Pascal } function divisionRapide( U : poly ; V : poly) : poly

Question 13 Écrire la fonction moduloRapide qui prend comme arguments deux polynômes

(toujours soumis à la contrainte

); et qui calcule le reste de la division euclidienne de

par

, plus rapidement qu'avec la fonction modulo de la question II.9. Quelle est la complexité de la fonction moduloRapide?

(* Caml *) moduloRapide : poly -> poly -> poly
{ Pascal } function moduloRapide( U : poly ; V : poly) : poly

Partie IV. Codage par évaluation multi-points

L'objectif de cette partie est de proposer un autre algorithme pour calculer le codage de ReedSolomon par une stratégie de type « diviser pour régner ».

On commence par construire un arbre binaire dont les nœuds sont étiquetés par des polynômes. Un arbre de sous-produits pour les polynômes

est défini comme suit : les

sont les étiquettes des feuilles de l'arbre (par ordre des indices

croissants dans l'ordre de lecture des feuilles de la gauche vers la droite), chaque nœud interne est étiqueté par le produit des polynômes étiquetant ses nœuds fils. Un arbre de sous-produits est dit optimal s'il est de hauteur

minimale

, et si les degrés des polynômes étiquetant deux fils d'un même nœud diffèrent d'au plus un. La figure 2 représente un tel arbre de sous-produits de hauteur

pour une famille de 6 polynômes

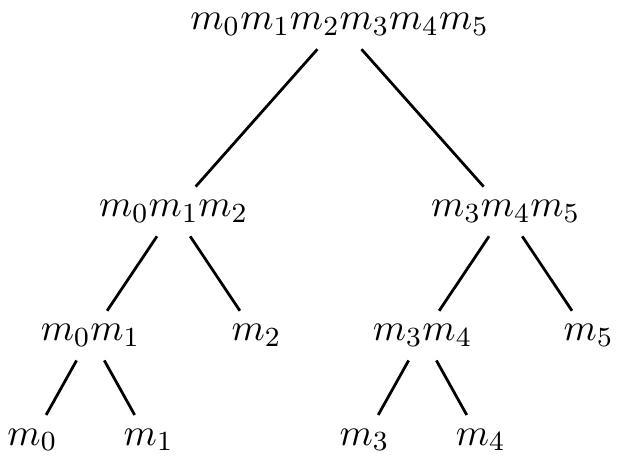
Fig. 2: Un arbre de sous-produits optimal pour

, avec la notation

Un arbre de sous-produits est représenté par une valeur de type arbre, défini comme suit :

    (* Caml *)
type arbre = Vide
| Noeud of poly * arbre * arbre

        { Pascal }
type arbre = `noeud;
    noeud = record etiquette: poly;
    filsG: arbre; filsD: arbre;
end;

L'arbre vide (sans aucun nœud) est représenté par Vide en Caml et par nil en Pascal.

Question 14 Écrire la fonction arbreSousProduits qui prend comme argument la liste

; et qui retourne un arbre de sous-produits optimal pour la suite de

polynômes

. Dans le cas où on a

, quelle est la complexité de la fonction arbreSousProduits? On donnera deux résultats, selon que la multiplication est réalisée avec produit ou produitRapide.

(* Caml *) arbreSousProduits : poly -> arbre
{ Pascal } function arbreSousProduits( \alpha: poly) : arbre

On souhaite maintenant calculer un second arbre, appelé arbre des restes de

. Il est similaire à l'arbre de sous-produits calculé à la question précédente, mais les étiquettes des nœuds diffèrent : à un nœud d'étiquette

dans l'arbre des sous-produits, correspond un nœud d'étiquette

dans l'arbre des restes. La figure 3 donne l'arbre des restes de

qui correspond à l'arbre de la figure 2.

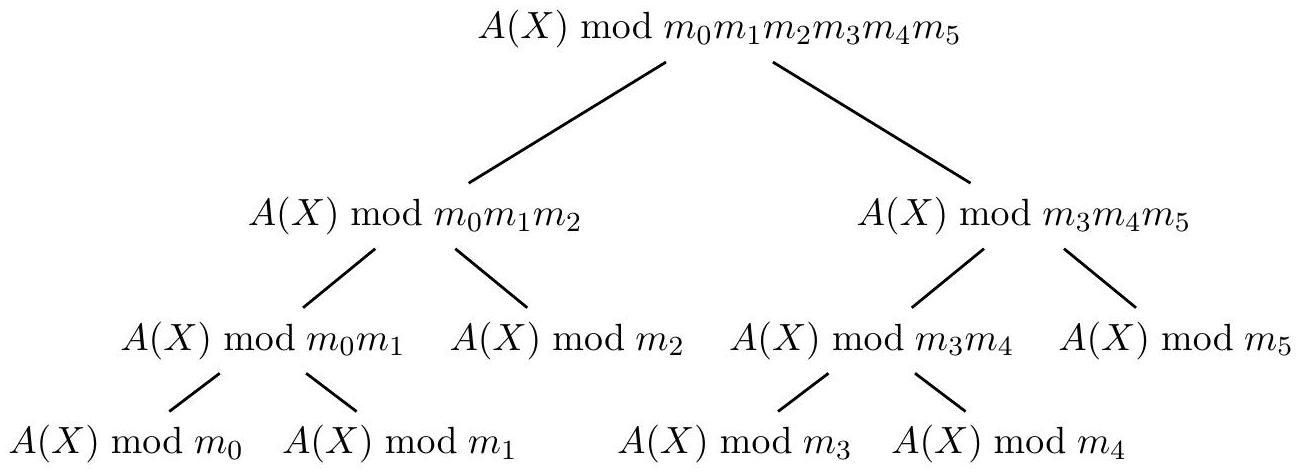
Fig. 3: Arbres des restes de

correspondant à la figure 2.

On fait l'observation suivante. Soient

trois polynômes à coefficients dans

. Si on connaît

, on peut calculer

par l'opération :

Question 15 Écrire la fonction arbreRestes qui prend comme arguments l'arbre des sousproduits et un polynôme

; et qui retourne comme résultat l'arbre des restes de

. Quelle est la complexité de la fonction arbreRestes lorsqu'on utilise les fonctions de la partie III? Quelle est la complexité lorsqu'on ne les utilise pas?

(* Caml *) arbreRestes : arbre -> poly -> arbre
{ Pascal } function arbreRestes( T : arbre ; A : poly) : arbre

À présent, on se sert de l'arbre des sous-produits pour factoriser les évaluations du même polynôme

aux nombreux points

. On remarque qu'on a pour tout

Et on calcule ces valeurs à partir de

à l'aide de l'arbre des restes.

Question 16 Écrire la fonction codageArbre qui prend comme arguments la liste

et le polynôme

; et qui retourne le codage de Reed-Solomon du message

en utilisant l'arbre de sous-produits correspondant à la suite des polynômes

. Déterminer sa complexité.

(* Caml *) codageArbre : poly -> poly -> poly
{ Pascal } function codageArbre(\alpha : poly ; A : poly) : poly