L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
On se contentera, pour les applications numériques, d'un seul chiffre significatif.

Miroir à atomes

Ce problème traite de la réalisation et de l'utilisation d'un miroir à atomes. Ce dispositif permet à la fois de mesurer quantitativement la force de van der Waals et de mesurer les rugosités d'une surface. Il se compose d'un texte de 3 pages, de trois figures et de 35 questions d'analyse et de compréhension auxquelles le candidat doit répondre. Ces questions sont regroupées en quatre parties et leur ordre suit le texte.

Commencez par lire attentivement le texte intitulé "L'atome devant son miroir". Cela devrait vous prendre entre 25 et 30 minutes. N'hésitez pas à surligner ou à relever les éléments qui vous paraissent importants.

Puis répondez aux questions de la partie intitulée "Analyse de l'article". Elles ne sont pas forcément ordonnées par difficulté croissante et certaines d'entre elles ont une formulation ouverte. Dans ce cas, toutes vos initiatives de résolution sont bienvenues à condition de justifier et de détailler systématiquement votre démarche. Si nécessaire, vous citerez précisément la partie du texte qui appuie votre raisonnement (les lignes sont numérotées de 1 à 246 à cet effet). Les hypothèses des modélisations doivent être clairement précisées et toutes les approximations doivent être explicitées et justifiées. Les calculs devront être menés sous forme littérale, avec pour objectif final d'obtenir une valeur numérique.

Données utiles pour l'analyse du texte

Nombre d'Avogadro
Constante de Boltzmann
Constante de Planck réduite
Accélération de la pesanteur
Masse molaire du rubidium

L'atome devant son miroir*

Abstract

Résumé Les progrès du refroidissement d'atomes par laser ont permis de contrôler le mouvement des atomes. De cette maîtrise est née l'optique atomique qui, après l'optique électronique et l'optique neutronique, étend le champ de l'optique à des objets plus gros et plus complexes. Nous nous sommes particulièrement intéressés à un composant optique de base, le miroir. En se réfléchissant à sa surface, les atomes nous informent sur leur interaction avec celle-ci.

Depuis plusieurs années les faisceaux laser permettent de refroidir des atomes neutres jusqu'à des températures de l'ordre du microkelvin. La réduction de l'agitation de ces atomes les rend manipulables et a permis de fonder une véritable optique atomique. Les rayons sont les trajectoires des atomes que l'on dévie, réfléchit ou focalise en utilisant toute une panoplie de forces exercées par des faisceaux laser et des champs magnétiques. L'optique atomique a également
ses ondes et les longueurs d'onde de de Broglie associées sont d'autant plus grandes que les atomes sont plus lents, de un à quelques centaines de nanomètres. L'optique atomique utilise deux types de miroirs : le miroir magnétique et le miroir à onde évanescente. C'est en cherchant à améliorer la qualité de ces derniers que nous avons mis en évidence leur sensibilité à l'interaction de van der Waals ou à la rugosité

1 Réfléchir un atome sur un miroir de lumière

Le miroir est constitué d'un prisme de verre à la surface duquel on forme une onde évanescente. Cette onde est obtenue par réflexion totale à l'intérieur du prisme de l'onde lumineuse monochromatique issue d'un laser (figure 1). Pour obtenir la réflexion totale, il faut que l'angle d'incidence du faisceau laser dépasse un angle limite. Si la lumière ne peut plus se propager vers l'extérieur du prisme, la continuité du champ électromagnétique à l'interface impose l'existence d'un champ non nul à l'extérieur, qui décroît exponentiellement en s'éloignant de la surface : c'est l'onde évanescente. Pour des incidences pas trop proches de l'angle limite, sa longueur caractéristique de décroissance est de l'ordre de

(

est la longueur d'onde du laser).

Le prisme est placé dans une enceinte à vide. Lorsqu'un atome approche de sa surface, il rencontre un champ électromagnétique d'intensité croissante et subit donc une force dipolaire, répulsive si la fréquence du laser est supérieure à la fréquence de résonance de la transition atomique (voir appendice).

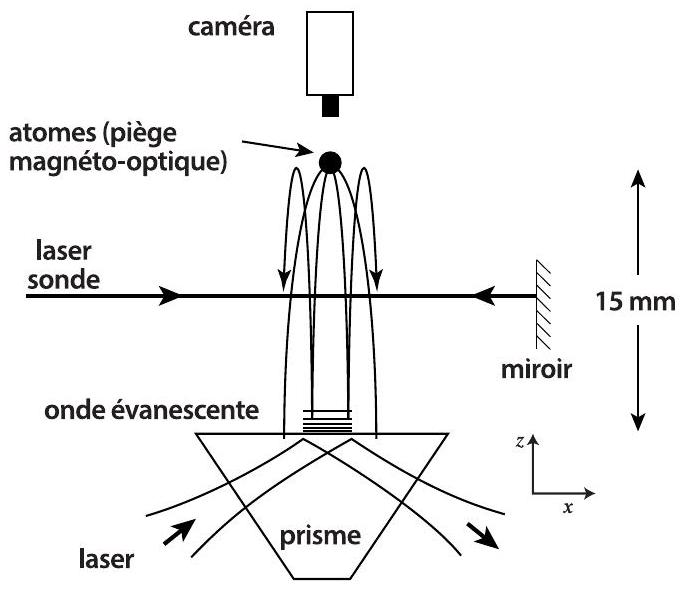
Figure 1: L'onde évanescente est créée par réflexion totale d'un laser à la surface d'un prisme. Les atomes tombent du piège magnéto-optique puis sont réfléchis par l'onde évanescente. Leur fluorescence est observée quand ils traversent le laser sonde.

L'onde évanescente crée ainsi une barrière de potentiel qui croît exponentiellement lorsque l'atome s'approche de la surface du prisme où

La source d'atomes froids est un piège combinant des faisceaux lasers et un champ magnétique. Il contient 100 millions d'atomes dans une sphère d'un millimètre de diamètre et les maintient à une température voisine de

. On ouvre le piège en coupant les faisceaux laser et le champ magnétique. Les atomes acquièrent alors une vitesse de

au bout d'1 centimètre de chute libre et peuvent rebondir sur la surface horizontale du miroir à atomes. Pour observer leur rebond, on les illumine avec un laser se propageant horizontalement entre le piège et la surface du miroir (figure 1). On détecte alors la très faible absorption de ce laser au passage des atomes, avant et après le rebond, ou on peut capter la lumière diffusée par les atomes grâce à une caméra très sensible.

2 Caractériser l'interaction d'un atome avec une surface

une vitesse thermique ordinaire ou avec des atomes ralentis. Nous avons choisi la deuxième méthode, dans une expérience consistant à lâcher des atomes froids sur une surface. cinétique est inférieure à

rebrousse chemin avant d'atteindre la surface. L'intensité laser utilisée (quelques watts par

) correspond à une énergie

de l'ordre de

joule. Des atomes de rubidium ayant cette énergie ont une vitesse d'environ

. À température ambiante la vitesse d'un atome est de l'ordre de quelques centaines de

. Pour le faire rebondir, il faut donc que la composante de sa vitesse normale à la surface soit sensiblement diminuée. Cela peut être obtenu en incidence rasante avec des atomes ayant une vitesse thermique ordinaire ou avec des atomes ralentis. Nous avons choisi la deuxième
méthode, dans une expérience consistant à lâcher méthode

atomes froids sur une surface.
elle atteint une valeur maximale

(voir figure 2 à gauche). Un atome dont l'énergie
dipolaire à une distance connue entre l'atome et la paroi. La figure 2 (droite) représente l'énergie potentielle qui correspond aux deux forces en fonction de la distance

à la paroi. Au potentiel dipolaire déjà présenté s'ajoute le potentiel de van der Waals qui varie en

. La somme des deux potentiels présente un maximum pour une distance d'environ 50 nm . Les atomes froids permettent de sonder cette barrière de potentiel.

Dans une expérience de chute libre, l'énergie cinétique des atomes est fixée par l'altitude initiale. On pourrait choisir d'augmenter cette hauteur jusqu'à ce que les atomes ne rebondissent plus. Dans la pratique, il est plus simple de fixer la hauteur de chute et de baisser l'intensité du laser, donc la valeur du potentiel dipolaire, jusqu'au seuil de réflexion des atomes. On mesure ainsi la valeur du maximum du potentiel total et, puisqu'on connaît la valeur du potentiel dipolaire, on obtient une mesure du potentiel de van der Waals à une distance donnée. Il est intéressant de noter qu'il existe une zone de transition autour du seuil de réflexion car l'atome peut passer à travers la barrière par effet tunnel, ou être réfléchi audessus de la barrière (réflexion quantique). Dans notre expérience, cette zone de transition n'a pas été observée car sa largeur, de quelques centièmes de l'énergie cinétique incidente, est masquée par la dispersion en énergie des atomes et les fluctuations d'intensité du laser. Le seuil de réflexion observé est en bon accord avec le modèle de l'interaction de van der Waals évoqué plus haut.

3 Mesurer les rugosités de surface

Nous avons été surpris d'observer qu'une très petite variation de la distance minimale d'approche, due par exemple à un défaut de la surface de l'ordre du nanomètre, modifiait de façon notable la trajectoire des atomes réfléchis. En fait, la rugosité de la surface se traduit par une perturbation du champ lumineux de l'onde évanescente. Cette perturbation conduit à une modification du potentiel dipolaire sur lequel rebondissent les atomes et donc à une modification de leurs trajectoires.

Pour étudier la sensibilité du dispositif à la rugosité de la surface, nous avons fait rebondir les atomes sur une structure régulière connue. Pour cela, nous avons réalisé un réseau de diffraction à atomes via une modulation périodique de l'onde évanescente. Dans ce but, le faisceau laser est partiellement réfléchi de sorte à interférer avec l'onde aller. Il en résulte une modulation spatiale du potentiel répulsif de forme sinusoïdale (voir figure 3 , à gauche). La période de modulation est fixée à environ la moitié de la longueur d'onde lumineuse. La profondeur de modulation des surfaces équipotentielles, qui résulte de l'interférence entre l'onde incidente et l'onde réfléchie, est réglable via la fraction

d'intensité réfléchie. On montre que la profondeur de modulation est une fraction

de la longueur d'onde lumineuse,

étant le contraste de l'interférence entre l'onde incidente et l'onde réfléchie. Pour que la diffraction

Un atome neutre plongé dans un champ électrique voit son nuage électronique déformé de sorte qu'un dipôle électrique est induit. Le moment de ce dipôle

est lié à l'amplitude du champ électrique

par la relation

où

est la polarisabilité de l'atome qui dépend de la pulsation d'oscillation

du champ électrique.

La polarisation induite de l'atome résulte du déplacement des charges sous l'effet du champ électrique extérieur. Pour modéliser ce phénomène, on suppose que le noyau est immobile. Il soumet l'électron de charge

à une force de rappel élastique

, où

désignent respectivement la masse de l'électron et sa position relativement au noyau, tandis que

est la pulsation fondamentale de l'oscillateur atomique. Si l'on suppose que le champ électrique

est uniforme à l'échelle de l'atome, l'électron subit aussi une force

. Ce modèle très
soit observable, il faut que la profondeur de modulation des surfaces équipotentielles, qui jouent le rôle de miroir atomique et qui produisent donc la modulation des ondes atomiques réfléchies, soit de l'ordre de la longueur d'onde de de Broglie

de l'onde atomique incidente. Comme cette longueur d'onde est de l'ordre de 8 nm pour du rubidium arrivant à

, il faut que l'intensité réfléchie soit très faible, de l'ordre de

de l'intensité incidente.

Ces résultats débouchent sur la possibilité d'analyser la rugosité de la surface du prisme avec une sensibilité inférieure au nanomètre. En effet, le cas d'une surface rugueuse peut s'interpréter comme une multitude d'interférences entre l'onde lumineuse incidente et les ondes diffusées par les défauts de la surface. Ceci crée des réseaux de diffraction d'orientation et de périodes variables qui conduisent donc, non plus à des ordres de diffraction bien distincts, mais à un élargissement global du nuage d'atomes. L'analyse détaillée de cet élargissement permet de caractériser quantitativement la rugosité de la surface.

Finalement, le rebond d'un atome permet de sonder la surface-miroir avec une résolution de l'ordre d'une fraction de

dans la direction perpendiculaire à celle-ci. Le grand intérêt de cette méthode est que l'atome perturbe très peu le champ analysé. En contrepartie, il faut effectuer une moyenne sur un grand nombre d'atomes pour obtenir un signal utilisable.

Appendice

simple, dit de l'électron élastiquement lié, permet de déterminer la polarisabilité

de l'atome en régime forcé.

La moyenne temporelle de l'énergie potentielle du dipôle atomique induit, plongé dans le champ électrique

, vaut

. Dans un champ inhomogène, un atome subit une force qui dérive de cette énergie potentielle. Au voisinage d'une résonance atomique, la polarisabilité peut atteindre des valeurs importantes. Elle devient négative pour des fréquences plus élevées que celle de la résonance : c'est cette situation, où le dipôle induit oscille en opposition de phase par rapport au champ, qui est utilisée dans le miroir à atomes. Dans ce cas, l'atome est expulsé des régions de champ fort par une force qui dépend de

, c'est-à-dire de l'intensité du laser qui crée le champ.

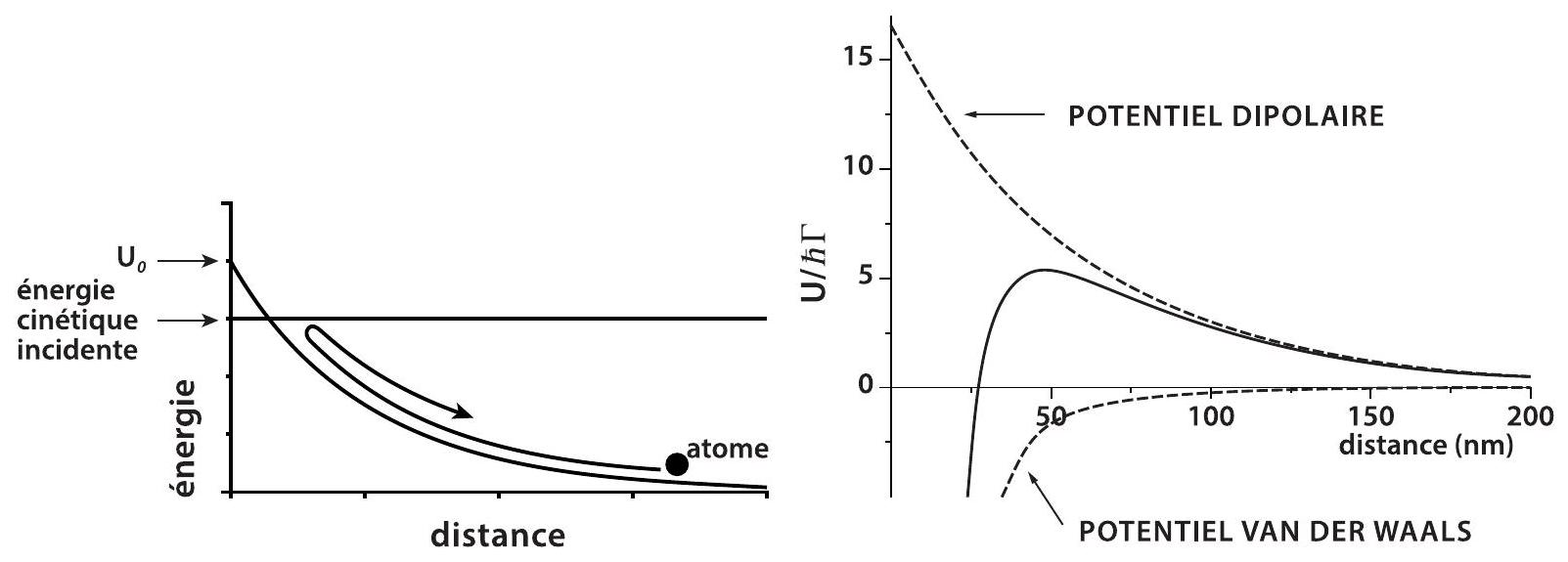
Figure 2: A gauche : L'onde évanescente crée un potentiel d'interaction qui décroît exponentiellement en fonction de la distance du prisme. Les atomes sont réfléchis si leur énergie cinétique est inférieure à la valeur maximale de l'énergie potentielle. A droite : Le potentiel total auquel sont soumis les atomes (trait plein) est la somme du potentiel dipolaire et du potentiel de van der Waals (en pointillé). Il est représenté en fonction de la distance au prisme. L'unité d'énergie est

où

est la largeur naturelle de la transition atomique utilisée pour le rubidium. Les valeurs correspondent aux conditions de l'expérience décrite dans le texte.

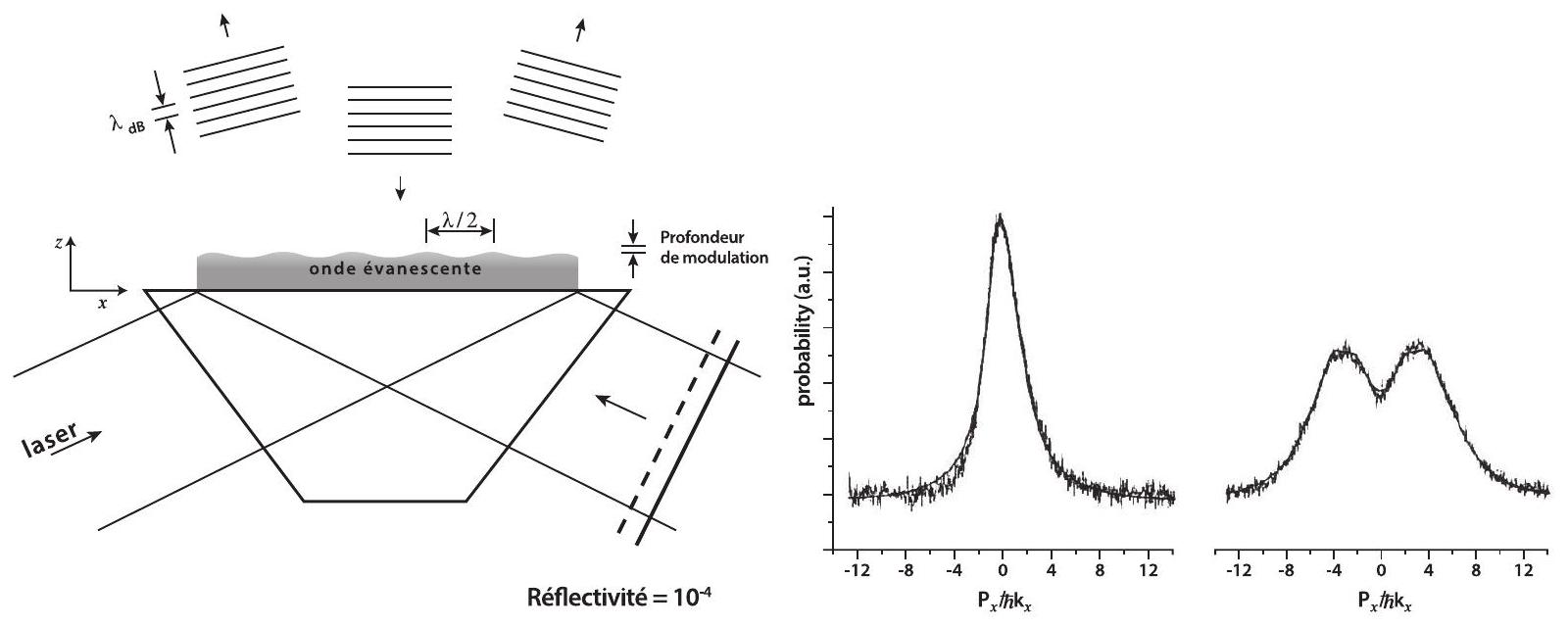
Figure 3: A gauche : Réseau de diffraction à atomes. Une petite fraction de la lumière incidente est renvoyée vers le prisme, créant une onde évanescente légèrement modulée. La profondeur des surfaces équipotentielles (amplitude verticale entre les sommets et les creux) est beaucoup plus petite que sa période. Une onde de de Broglie atomique subit une forte diffraction si

est de l'ordre de cette profondeur de modulation. Puisque

, les atomes sont sensibles à de très faibles déformations de l'onde évanescente. A droite : Mesure de la probabilité de diffraction atomique (en unité arbitraire) en fonction de la quantité de mouvement transverse

de l'atome en unité de

. La partie gauche correspond à la réflexion sur une surface plane. La partie droite représente la figure de diffraction sur un réseau de lumière pour lequel

. Les pics correspondent aux deux premiers ordres diffractés (en

) qui ne sont pas résolus.

Analyse de l'article

I - Onde évanescente

Démontrer la condition d'obtention de la réflexion totale (lignes 27-29). Vous appuierez votre raisonnement par un schéma. Déterminer l'angle limite si l'indice optique du prisme vaut .

Les questions qui suivent ont pour but de modéliser l'onde évanescente (lignes 29-37). On note

les vecteurs d'onde complexes du faisceau laser incident dans le prisme et de l'onde évanescente dans le vide, respectivement, et on repère par les indices

leurs composantes tangentielles et normales à la surface du prisme.
2. Expliquer pourquoi les composantes tangentielles

sont égales.
3. En déduire la relation liant

et l'indice

pour un angle d'incidence

.
4. Retrouver la condition de réflexion totale et, quand elle est vérifiée, donner l'expression de la longueur caractéristique de décroissance de l'onde évanescente, qu'on notera

.
5. Tracer l'allure de la variation de

en fonction de l'angle d'incidence

. Commenter les lignes 34 à 37 du texte.

II - Rebond des atomes

En utilisant la modélisation exposée dans l'appendice (lignes ), déterminer l'expression de la polarisabilité en fonction de et . Quelle est son unité ?
Justifier l'expression de donnée dans l'appendice, ligne 234.
Justifier les lignes 39-44.
Expliquer les lignes 45-49.
Expliquer pourquoi les atomes rebroussent chemin (lignes et figure 2 à gauche).
Vérifier que les valeurs de et de la vitesse des atomes de rubidium indiquées lignes sont bien cohérentes entre elles.
Expliquer quantitativement les lignes 55-57.
Expliquer les lignes 57-62. Préciser quantitativement ce que signifie "incidence rasante".
Estimer la densité volumique d'atomes dans le piège et la comparer avec la densité de molécules dans l'air ambiant.
Estimer la pression dans le piège en supposant que les atomes froids se comportent comme un gaz parfait. Quelle contrainte expérimentale en découle ?
Vérifier la valeur de la vitesse de chute des atomes indiquée ligne 72 .

III - Interaction d'un atome avec une surface diélectrique

Tracer l'allure des lignes du champ d'un dipôle électrique.
En déduire pourquoi un dipôle permanent est attiré par son dipôle image dans une paroi diélectrique (lignes 94-97) et justifier la dépendance en indiquée ligne 119 .
Expliquer les lignes 103 à 108.
L'ordre de grandeur de la distance minimale atome-paroi donnée dans le texte vérifie-t-elle la condition énoncée aux lignes 107-108 ?
Le potentiel dipolaire est de la forme et le potentiel de van der Waals est de la forme . Quel est le signe de ? Décrire le comportement asymptotique du potentiel total pour et .
Construire avec et une quantité sans dimension proportionnelle à .
Tracer l'allure du potentiel total dans les limites et . De quelle limite se rapproche la figure 2 à droite ?
Écrire, sans les résoudre, les deux équations permettant de déterminer en fonction de l'altitude initiale des atomes, qu'on notera , et de la valeur de correspondant au seuil de réflexion des atomes (lignes 123-134).

On rappelle que la probabilité de transmission

par effet tunnel (lignes 134-143) à travers une barrière de potentiel rectangulaire de largeur

et de hauteur

, pour un atome de masse

dont l'énergie cinétique

est inférieure à

, vaut environ

.
25. De quel autre phénomène physique rencontré dans l'article peut-on rapprocher l'effet tunnel ? Vous argumenterez votre réponse.
26. On cherche l'expression de

pour estimer le coefficient de transmission à travers le potentiel de la figure 2 (droite) lorsque l'énergie cinétique

de l'atome est inférieure à la valeur maximale du potentiel total, qu'on notera

. Expliquer au moyen d'un schéma comment on peut, pour ce calcul, approcher le potentiel total par une barrière rectangulaire.
27. Comment varie la largeur de cette barrière en fonction de

lorsque l'énergie cinétique

est juste inférieure à

? En déduire comment, dans cette approximation, la probabilité de transmission varie avec

. Proposer une expression littérale de la largeur de la zone de transition sur laquelle on observe l'effet tunnel (lignes 134-143).

IV - Mesure des rugosités de surface

Donner l'expression de l'amplitude de l'onde évanescente résultant du faisceau laser incident en fonction de et . Par analogie, en déduire l'amplitude de l'onde évanescente résultant du faisceau laser réfléchi sur le miroir de réflectivité .
En déduire que le potentiel répulsif qui en résulte se met sous la forme

où

est une constante de normalisation.
30. Exprimer

en fonction de

sur une équipotentielle dans le cas où

. Dans ce cas, représenter graphiquement quelques équipotentielles.
31. Donner l'expression de la profondeur des équipotentielles dans cette approximation.
32. Rappeler la définition de la longueur d'onde de de Broglie et retrouver son ordre de grandeur pour le rubidium (lignes 183-185).
33. Montrer que les conditions expérimentales de la figure 3 correspondent bien au régime où la diffraction doit être observable.
34. Retrouver l'ordre de grandeur de

(lignes 185-187).
35. Calculer à quel angle de diffraction correspondent les pics sur la figure 3 à droite.

*Texte extrait et adapté d'un article publié dans la revue Images de la physique en 1998.