NB : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction.
Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

Conformément à l'usage international, les vecteurs sont représentés en gras.

- PARTIE A -

1. Modèle de Thomson de l'atome d'hydrogène

On donne:

.
1.1 Dans un modèle classique de l'atome d'hydrogène, dû à J.J. Thomson (1895), le noyau positif de charge totale

est modélisé par une sphère uniformément chargée de rayon

Quelle est la densité volumique de charge correspondante (expression littérale et valeur numérique) ?
Expliciter en tout point de l'espace le champ électrostatique créé par cette distribution de charge.
1.2 Un électron de masse et de charge , supposé ponctuel, est placé au centre de cette distribution.
Montrer que, si l'on écarte l'électron de cette position d'une quantité , il est soumis à une force de rappel que l'on explicitera.
Quelle est l'intensité de cette force pour ?
Quel sera le mouvement ultérieur de l'électron s'il est lâché, sans vitesse initiale, à partir d'un point caractérisé, dans un repère cartésien centré sur le noyau, par , ?
1.3 On superpose au champ créé par le noyau, un champ uniforme .
Montrer que, si ce champ est suffisamment faible, l'électron prend une nouvelle position d'équilibre tout en restant lié au noyau.
Pour quelle valeur numérique maximum de cette position existe-t-elle?
Quel est, dans cette position, le moment dipolaire de la distribution de charge ? Ce moment dépend-t-il du choix de l'origine des coordonnées que nous avons fait?
On pose où est la polarisabilité électronique. Quelle est la dimension physique de ? A quelle caractéristique physique de l'atome peut-on la comparer? Quelle est sa valeur numérique pour le modèle de Thomson?
1.4 Le champ appliqué est maintenant variable dans le temps avec une pulsation .
En négligeant tout autre effet éventuel et en supposant que le champ est d'amplitude suffisamment faible (inférieure à la valeur trouvée en 1.3.2), écrire l'équation du mouvement de l'électron sous l'action combinée des champs et .
Donner sa solution en régime sinusoïdal permanent.
En déduire l'expression de la polarisabilité en fonction de la pulsation .
Représenter sommairement le graphe de la fonction .

2. Etude du champ électrique dans un plasma

Un plasma est constitué de deux types de particules chargées. On notera respectivement

la densité particulaire des charges positives et négatives. Dans le cadre d'une modélisation analogue à celle du modèle de Thomson, la distribution de charges positives est supposée uniforme dans l'espace. Les charges négatives (électrons) sont libres de se déplacer. A l'équilibre, la charge volumique

, le champ et le potentiel sont nuls en tout point. On suppose désormais que le déplacement des charges négatives se fait uniquement suivant la direction

et que les charges positives sont fixes dans le référentiel d'étude.

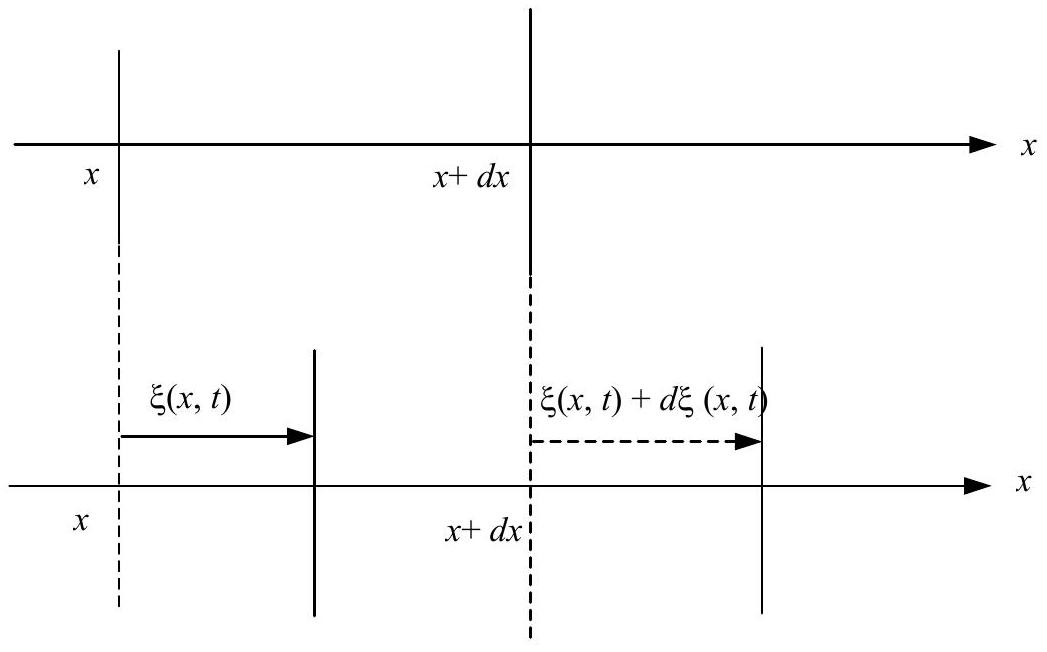
Figure 1

2.1 Sous l'effet d'une perturbation, les électrons contenus initialement dans une tranche cylindrique de base

dans le plan d'abscisse

et d'épaisseur

se retrouvent dans une tranche de base

dans le plan d'abscisse

et d'épaisseur

avec

(voir figure 1). On suppose que le milieu non perturbé est localement neutre.

En écrivant la conservation du nombre des électrons contenus initialement dans la tranche cylindrique de base et d'épaisseur , établir l'expression de la variation de la densité particulaire d'électrons en fonction de et de .
Exprimer la charge volumique et le moment dipolaire volumique résultant de ce déplacement en fonction de et .
En utilisant l'équation de Maxwell Gauss, donner l'expression en fonction de et du champ électrique créé dans le plasma par cette distribution de charge.
Quelle est alors la relation entre le champ créé par la matière polarisée et le moment dipolaire volumique ?
Ecrire l'équation du mouvement pour un électron soumis à ce seul champ et dont le déplacement par rapport à l'équilibre est .
Montrer que le plasma peut être le siège d'oscillations spontanées de la charge volumique électronique et expliciter leur pulsation en fonction des constantes et et de la densité électronique .
Quelle est la valeur de pour ?
2.2 Le plasma est soumis à un champ appliqué variant dans le temps avec une pulsation .
Ecrire l'équation du mouvement d'un électron sous l'action combinée du champ appliqué et du champ créé par le plasma polarisé.
Etablir la relation entre le moment dipolaire volumique et le champ appliqué en fonction de et .
En déduire la relation entre le moment dipolaire volumique et le champ local en fonction de et . On posera , et on explicitera .

3. Onde électromagnétique dans un plasma

La perturbation évoquée ci-dessus est une onde électromagnétique plane polarisée rectilignement selon

de pulsation

dont le champ électrique s'écrit

. La vitesse des particules chargées restant faible par rapport à celle de la lumière, on néglige dans la suite l'effet du champ magnétique sur leur mouvement. On néglige également toute dissipation d'énergie. Dans ces conditions, la propagation d'une onde de pulsation

obéit à l'équation de
d'Alembert où l'on a simplement remplacé la permittivité du vide

par la valeur

Ecrire l'équation de d'Alembert pour une onde plane polarisée du type donné et en déduire la relation de dispersion .
Expliciter pour une telle onde, les vitesses de phase et de groupe.
Montrer que ne peuvent se propager que des ondes dont la fréquence est supérieure à une certaine valeur que l'on explicitera.
A.N. Le plasma ionosphérique correspond à une densité électronique . Calculer la fréquence de coupure en dessous de laquelle les ondes ne peuvent le traverser. Dans quel domaine du spectre électromagnétique se situe cette fréquence ?
En tenant compte du modèle proposé, expliquer ce que deviennent les ondes qui ne peuvent se propager dans ce plasma.

- PARTIE B -

Etude d'un étireur à réseaux

Dans le domaine de l'optique ultra-rapide, l'amplification des impulsions lumineuses se heurte à une difficulté majeure. En effet, lors de l'amplification, l'intensité crête, inversement proportionnelle à la durée des impulsions, peut prendre des valeurs bien supérieures au seuil de dommage du milieu amplificateur. Pour éviter cela, on utilise des dispositifs optiques permettant d'étirer temporellement l'impulsion avant amplification, et de la «re-comprimer» après amplification.
Dans ce problème on se propose d'étudier le principe d'un étireur d'impulsions constitué par l'association de deux réseaux à réflexion. Dans la première partie on étudiera les propriétés dispersives d'un seul réseau puis dans la deuxième partie, on étudiera celles résultant de l'association de deux réseaux identiques parallèles entre eux. Enfin, on étudiera dans la troisième partie le changement du profil temporel d'une impulsion de lumière se propageant dans ce dispositif optique.

1. Réseau à échelettes

On considère le réseau en réflexion dit à échelettes représenté dans la figure 1-a, constitué d'une succession de facettes réfléchissantes (largeur

) inclinées d'un angle

par rapport au plan du réseau. Une onde plane monochromatique (longueur d'onde

) éclaire le réseau sous un angle

par rapport à la normale

et on observe l'onde diffractée à l'infini dans la direction qui fait un angle

avec

. Les angles d'incidence et de diffraction par rapport à la normale de la facette sont respectivement

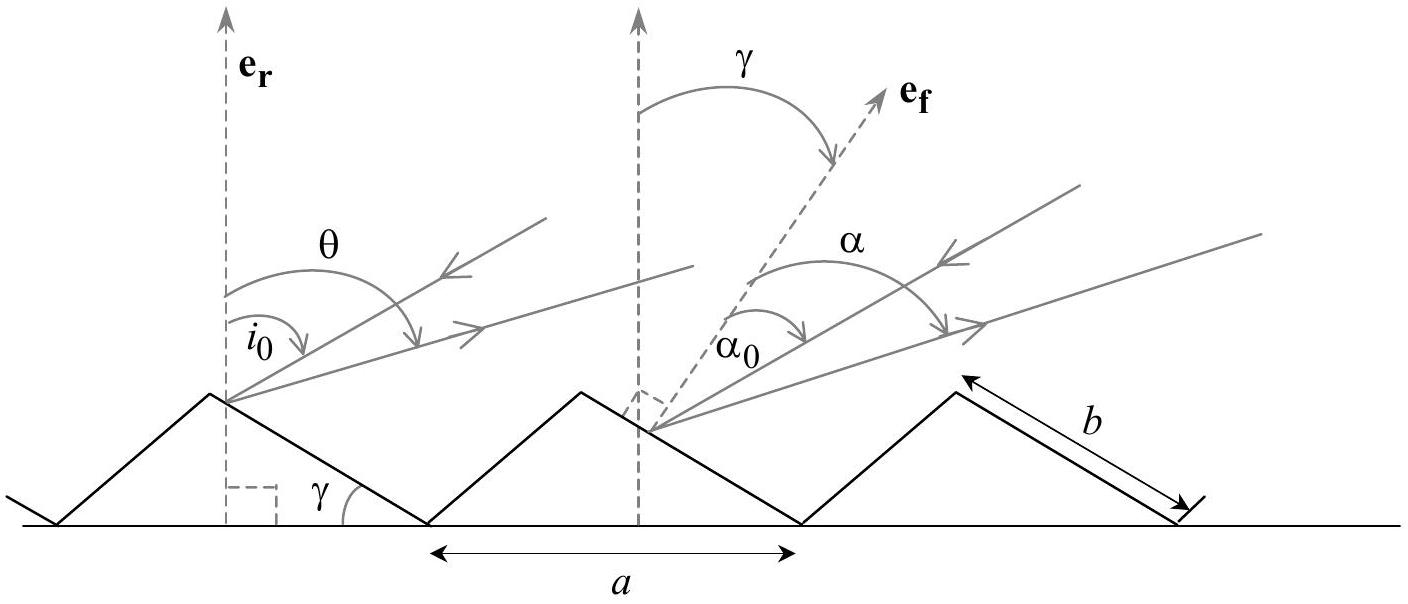
Figure 1-a

1.1. Diffraction par une facette

a. Exprimer la différence de phase entre les ondes véhiculées par deux rayons incidents dont l'un tombe sur une extrémité de l'arête de la facette en fonction de

et de la distance

(figure 1-b).
b. En déduire l'expression de l'amplitude diffractée par une facette dans la direction

.
c. Dans quelle direction de l'espace se situe le centre de la figure de diffraction ?

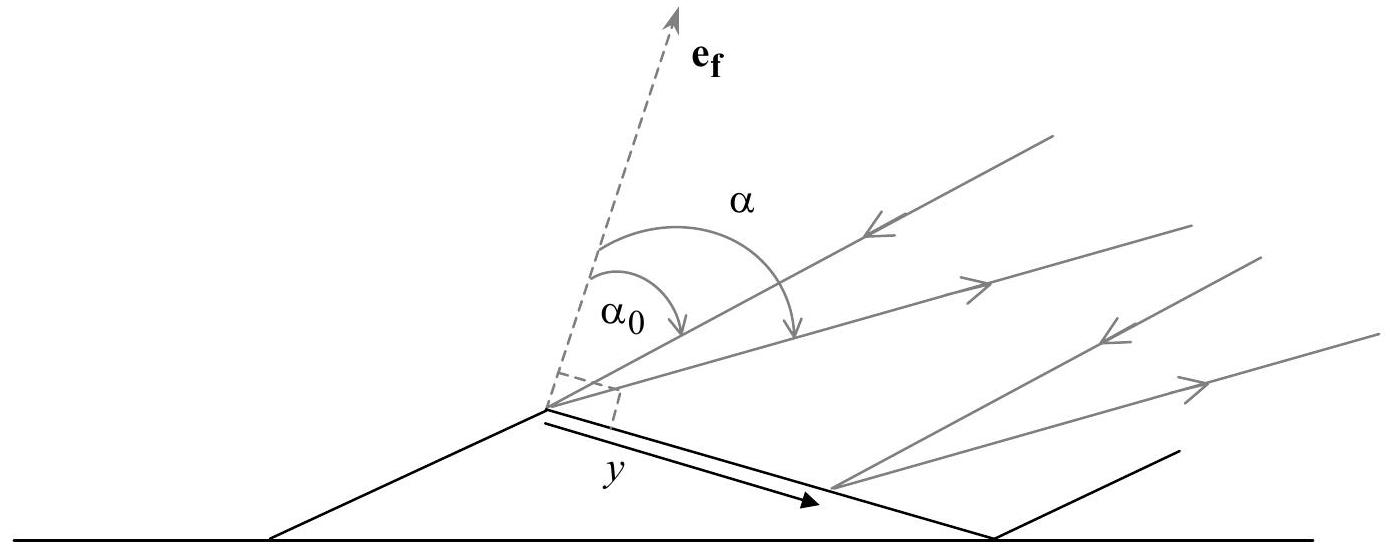
Figure 1-b

1.2. Diffraction par le réseau

a. Exprimer la différence de phase entre les ondes véhiculées par deux rayons homologues incidents tombant sur deux facettes consécutives, séparés d'une distance

et des angles

(figure 1-c).
b. En déduire la position des maxima principaux

en fonction de

et d'un nombre entier

.
c. On veut faire coïncider pour une longueur d'onde

l'ordre +1 du réseau avec le maximum de la courbe de diffraction d'une facette. Calculer la distance

entre les facettes qui permette de réaliser cette condition. Application numérique:

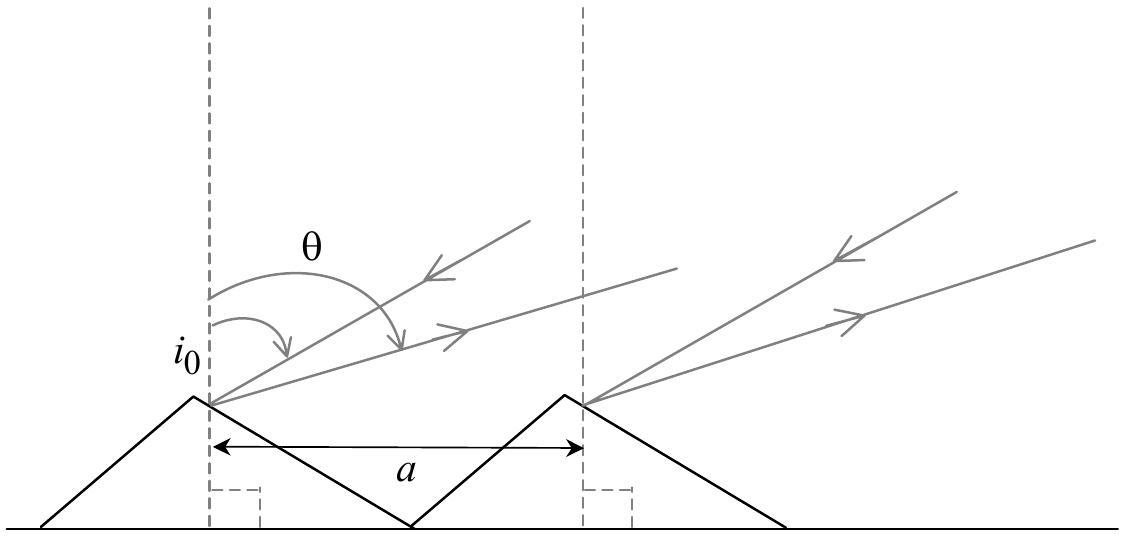
Figure 1-c

On suppose par la suite que la condition du 1.2.c est réalisée et que le réseau (avec

) se comporte comme un miroir, réfléchissant l'onde incidente dans la direction

donnée par

pour des longueurs d'ondes

proches de

et où

est la vitesse de la lumière (

). On néglige ainsi l'énergie répartie sur les autres maximums. On supposera aussi que la largeur du pic principal est négligeable.

2. Combinaison de deux réseaux à échelettes

On considère maintenant deux réseaux à échelettes (mêmes paramètres

) parallèles entre eux disposés comme le montre la figure (2). La distance

entre les réseaux est supposée être grande de sorte que l'on se trouve dans les conditions de diffraction à l'infini quand l'onde lumineuse irradie le réseau 2 . On envoie une onde plane véhiculée par le rayon incident faisant un angle

avec la normale au réseau 1 . L'onde à l'entrée du réseau 1 est une impulsion lumineuse qui s'écrit sous la forme

où

est une constante et

est la pulsation centrale. On définit les relations de passage entre une fonction complexe

et sa transformée de Fourier

est une fonction complexe de

. L'impulsion lumineuse peut être décrite comme une superposition d'ondes monochromatiques dont le poids de chaque composante est donné par

. On a dessiné sur la figure (2) le trajet correspondant à une onde de pulsation centrale

. On pose

.
On donne la relation

avec

réels et

.
On convient de définir la «largeur» d'une courbe comme la demi-largeur à

du maximum de cette courbe.

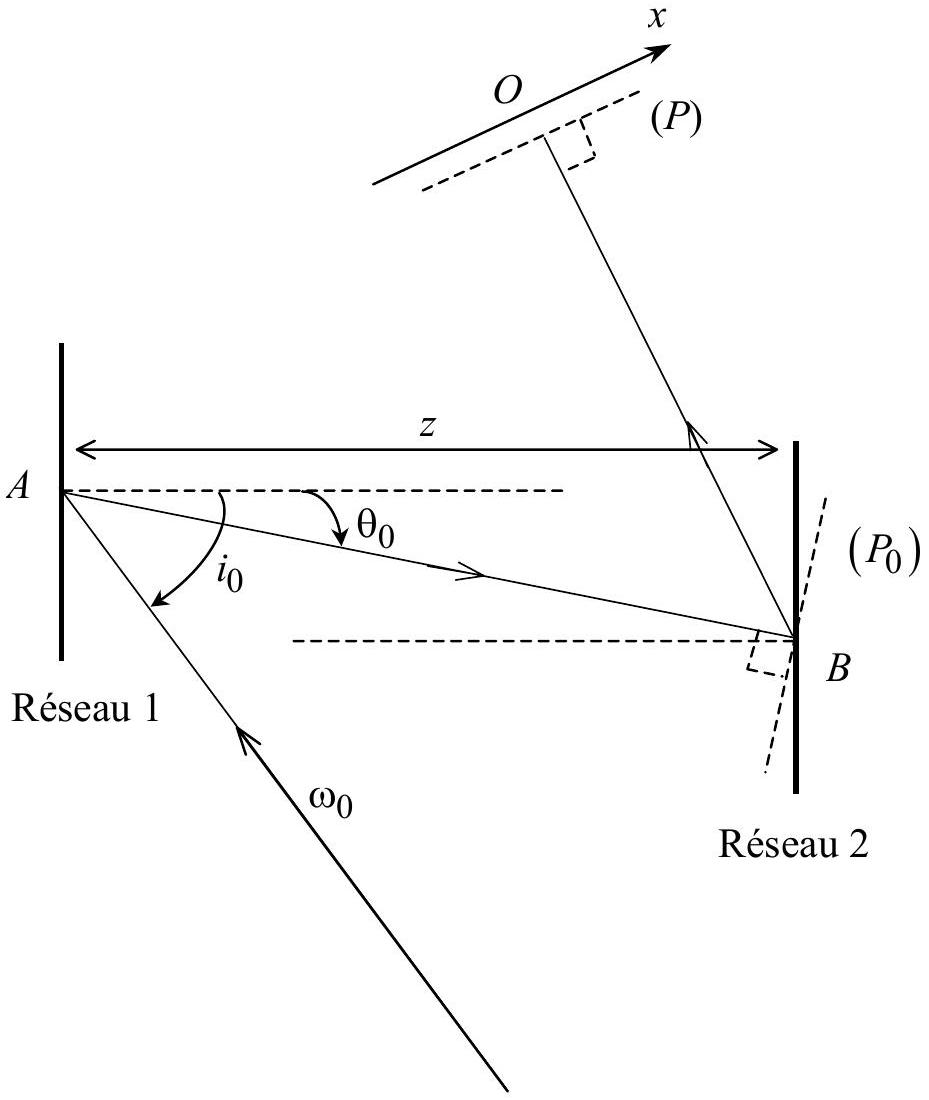
Figure 2

2.1. a. Donner la signification de

.
b. Calculer la transformée de Fourier

de l'impulsion.
c. En déduire sa «largeur».
2.2. a. Dans quelle direction, mesurée par rapport au rayon incident sur le réseau 1 , est diffracté le rayon lumineux associé à

après le deuxième réseau?
b. Dessiner le trajet d'un rayon correspondant à une composante spectrale

quelconque proche de

.
c. Conclure sur les directions des rayons diffractés par le deuxième réseau.
2.3. a. Pour une composante spectrale

, trouver la relation

donnant le point d'impact du rayon lumineux sur le plan d'observation

perpendiculaire au trajet du rayon associé à

. On prendra l'origine

pour

.
b. A partir de la relation

, trouver la relation entre

sachant que

est proche de

.
c. En déduire la relation

caractérisant l'étalement spatial du spectre de l'impulsion le long du plan

. On rappelle que

sont proches de

respectivement, et qu'un développement limité peut donc être effectué.
d. En ne tenant compte que de la dispersion spatiale déterminée précédemment, déterminer le profil spatial de l'intensité lumineuse au niveau de ce plan

.
e. Application numérique : Calculer

en degré puis la «largeur» de la courbe de l'intensité diffractée dans le plan

pour

, et

3. Etirement temporel d'impulsions lumineuses

La différence de phase totale

accumulée jusqu'au plan

entre deux rayons associés à

s'exprime à partir d'un développement limité à l'ordre 2 comme

où

.
3.1. En comparant à l'unité le terme de second ordre, pour quelles durées

la correction d'ordre deux est-elle nécessaire? On prendra

.
3.2 Le coefficient

peut être calculé en utilisant le fait que le déphasage quadratique au niveau du plan

est le même que le déphasage dans le plan

(figure 2) et est dû uniquement à la diffraction par le réseau 1 .
a. Calculer la phase accumulée par un rayon associé à

à partir du point d'impact

et diffracté dans le plan (

) en fonction de la distance

.
b. En déduire le coefficient

en fonction de

et l'angle de diffraction

. Application numérique.
3.3 a. En tenant compte du déphasage

, reconstituer le profil temporel du champ électrique de l'impulsion lumineuse au niveau du plan

.
b. En déduire le module du champ.
c. Quelle est la signification du coefficient

?
d. Donner la largeur temporelle

de l'impulsion au plan (

).
e. Application : On envoie une impulsion lumineuse dans ce dispositif telle que

. Calculer la durée de l'impulsion

Fin de l'énoncé