En 1923, le mathématicien George Pólya introduit une expérience d'urne aléatoire pour modéliser la propagation d'épidémies. Ce modèle, à base de tirages de boules colorées dans une urne, et ses généralisations ont donné naissance à un grand nombre d'études qui ont conduit à des applications variées, notamment en économie et en finance.
Au milieu des années 2000, le chercheur français Philippe Flajolet propose une nouvelle approche de ces modèles, à base de combinatoire et de séries génératrices. Sa méthode s'applique à la totalité des modèles d'urne dite «équilibrée», là où les techniques de résolution antérieures étaient spécifiques de chaque protocole de tirage. Cette épreuve est organisée en cinq parties dans une large mesure indépendantes :

dans la partie I, il est demandé de démontrer un résultat du cours qui est utilisé dans la partie IV ; le résultat de la question 6 sert dans la partie V ;
la partie II traite un cas particulier qui est généralisé dans la partie IV ;
la partie III introduit la méthode de Philippe Flajolet ;
les parties IV et V étudient deux protocoles différents de tirage ; la partie V permet également d'établir un lien avec certaines permutations d'un ensemble fini.

Notations

Dans tout le problème, on définit la famille de polynômes

par

On appelle fonction polynomiale de deux variables réelles

, toute combinaison linéaire d'applications de la forme

où

I Résultats préliminaires

Soit

un réel. On note

.
Q 1. Préciser le domaine de définition

. Justifier que

est de classe

sur

et donner une équation différentielle linéaire du premier ordre vérifiée par

sur

.
Q 2. Énoncer le théorème de Cauchy pour une équation différentielle scalaire linéaire du premier ordre et démontrer que, pour tout

Q 3. Rappeler la définition du produit de Cauchy de deux séries entières et énoncer le théorème qui s'y rapporte.
Q 4. En déduire que, pour tout entier

et tous réels

I.B -

Q 5. Pour

, donner la valeur de la somme de la série entière

ainsi que celle de sa dérivée.
Q 6. Démontrer par récurrence que, pour tout entier

, il existe un unique polynôme

tel que, pour tout

II Un modèle particulier d'urne de Pólya

On dispose d'un stock infini de boules noires et blanches. Une urne contient initialement une boule noire et une boule blanche. On effectue une suite de tirages selon le protocole suivant :

on tire au hasard une boule de l'urne;
on replace dans l'urne la boule tirée;
on ajoute dans l'urne une boule de la même couleur que la boule tirée.

On définit la suite

de variables aléatoires par

et, pour tout entier

donne le nombre de boules blanches dans l'urne après

tirages. On note

la fonction génératrice de la variable

. On rappelle que

.
Q 7. Déterminer les lois de

puis les fonctions

.
Q 8. Soient

deux entiers supérieurs ou égaux à 1 . Établir que

Q 9. En déduire que, pour tout entier

supérieur ou égal à 1 et tout réel

Q 10. Démontrer que, pour tout entier

et tout réel

Q 11. Identifier la loi de

et donner son espérance.

III Modèle général d'urne équilibrée

Dans cette partie, on généralise le modèle de la partie précédente.
Soient

six entiers naturels. On dispose à nouveau d'un stock infini de boules noires et blanches, mais celles-ci sont cette fois numérotées, à partir de zéro, de manière à pouvoir les différencier. L'urne contient initialement

boules blanches et

boules noires. On effectue une suite de tirages selon le protocole suivant:

on tire au hasard une boule dans l'urne;
on replace cette boule dans l'urne;
si la boule tirée est blanche, on ajoute dans l'urne boules blanches et boules noires;
si la boule tirée est noire, on ajoute dans l'urne boules blanches et boules noires.

On suppose que

, on dit alors que l'urne est équilibrée et on note

.
Pour

, une issue résultant de

tirages successifs est modélisée par le

-uple indiquant la couleur et le numéro des boules successivement obtenues. On note

l'ensemble des issues possibles de ces

tirages.
La figure 1 donne deux exemples de 3 tirages (

), pour

(modèle de la partie précédente). La boule au dessus de chaque flèche représente celle qui a été tirée.

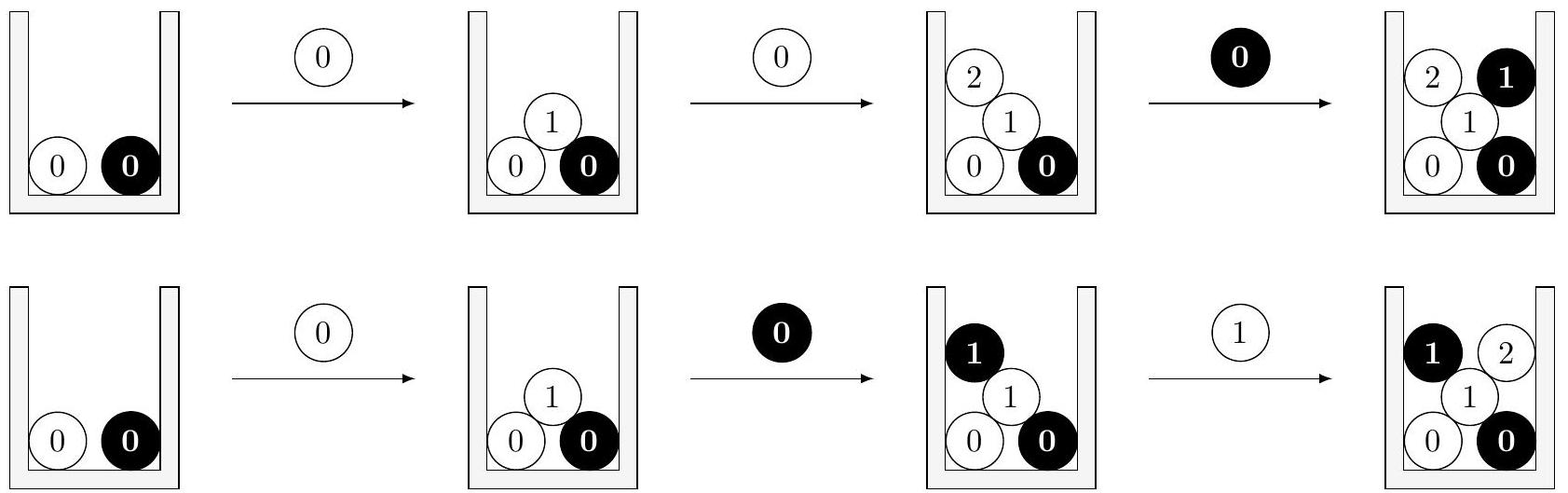
Figure 1 Deux exemples de 3 tirages

La première suite de trois tirages est modélisée par l'issue

; la deuxième suite est modélisée par l'issue

. On note que ces deux issues différentes aboutissent à la même composition de l'urne.

Pour

on note

(respectivement

), le nombre de boules blanches (respectivement noires) présentes dans l'urne à la fin des

tirages modélisés par

.
Pour tous réels

, on pose

.
Pour

, on note à nouveau

le nombre de boules blanches présentes dans l'urne après

tirages et

sa fonction génératrice.
Dans les deux questions suivantes, on suppose

. En d'autres termes, l'urne contient, au départ, une boule blanche et, à chaque tirage, on ajoute une boule de la couleur opposée à celle qui a été tirée.
Q 12. En dressant la liste de toutes les issues possibles, donner la loi de

.
Q 13. Vérifier que

.
On revient désormais au cas général d'une urne équilibrée.
Q 14. En examinant le nombre de boules dans l'urne juste avant chaque tirage, justifier que, pour

Q 15. Montrer que, pour tout

et tout

Justifier les égalités

Q 17. Démontrer que, pour tout entier

Pour tous réel

, on pose, sous réserve d'existence,

Soit

. On pose

.
Q 18. Justifier que, pour

assez petit, la fonction

est bien définie sur

.
On fixe un tel

dans toute la suite de cette partie.
Q 19. Justifier que

admet une dérivée partielle d'ordre 1 par rapport à

sur le domaine

, obtenue par dérivation terme à terme par rapport à

de l'expression de

.
Q 20. Démontrer que

admet une dérivée partielle d'ordre 1 par rapport à

sur le domaine

, obtenue par dérivation terme à terme par rapport à

de l'expression de

.
On admet qu'il en est de même pour la variable

.
Q 21. Vérifier que

puis que

est solution sur

de l'équation aux dérivées partielles

IV Modèle général d'une urne de Pólya

Dans cette partie, on considère le modèle d'urne équilibrée pour lequel

. On a donc nécessairement

. En d'autres termes, à chaque fois qu'on tire une boule, on ajoute

boules de sa couleur dans l'urne. La composition initiale de l'urne est de

boules blanches et

boules noires. Compte tenu des résultats de la partie III, on s'intéresse à l'équation aux dérivées partielles

d'inconnue

définie sur une partie de

avec la condition

On admet que la fonction

définie sur

par

est solution de l'équation (IV.1).
On reprend la notation de la partie précédente :

.
Q 22. À l'aide des résultats préliminaires, démontrer qu'il existe

tel que

et, pour tout

où

est une fonction polynomiale de deux variables à préciser.
Q 23. Justifier que

admet une dérivée partielle d'ordre 1 par rapport à

sur le domaine

, obtenue par dérivation terme à terme par rapport à

de l'expression de

.
Q 24. Démontrer que

admet une dérivée partielle d'ordre 1 par rapport à

sur le domaine

, obtenue par dérivation terme à terme par rapport à

de l'expression de

.
On admet qu'il en est de même pour la variable

.
Q 25. En déduire que, pour tout entier

, puis que

coïncident sur

, où

ont été définis dans la partie III.
Q 26. Conclure que, pour tout entier

et pour tout

Q 27. À l'aide du résultat précédent, retrouver celui de la question 10.
Q 28. À l'aide des résultats des questions 16 et 19 , déterminer l'espérance de

V Urne de Friedman et montées de permutations

Dans cette partie, on suppose que

, ce qui correspond au protocole utilisé dans les questions 12 et 13 (modèle introduit par Friedman en 1945).

On conserve toutes les notations de la partie III (tous les résultats de cette partie peuvent être admis). On a donc en particulier

. On admet, pour

assez petit, l'égalité

Q 29. À l'aide de la question 6, justifier que, pour tout entier

et tous

tels que

, la somme

est une fonction polynomiale de

.
On a donc, d'après la question 16 , pour tout entier

et tout

.
Dans toute la suite, on fixe un entier

.
Q 30. Montrer que

.
Q 31. En utilisant ce qui précède et en développant

, déterminer le développement limité de

à l'ordre

en 0 .
Q 32. En déduire que, pour tout

dans

V.B - Montées d'une permutation

Soit

une suite finie d'entiers, deux à deux distincts. Une montée (respectivement descente) de

est un indice

tel que

(respectivement

).
Q 33. Soit

un entier supérieur ou égal à

une suite finie d'entiers, et

un entier tel que

pour tout

. On insère la valeur

dans cette suite juste après

, avec

, de manière à obtenir la suite (

). Comparer le nombre de montées et de descentes de la nouvelle suite par rapport à l'ancienne. On distinguera deux cas.
On note

l'ensemble des permutations de

, c'est-à-dire des fonctions bijectives de

dans lui-même. On représente un élément

par la suite finie (

) et on appelle montée (respectivement descente) de

une montée de cette suite. Par exemple, avec

, la permutation

représentée par la liste

admet une montée et deux descentes. Pour tout entier

, on note

le nombre d'éléments de

avec

montées.
Q 34. Déterminer les éléments de

et calculer parmi eux le nombre de permutations avec

montées pour tout entier

. Comparer les valeurs obtenues avec les coefficients de

où

a été exprimé à la question 13.
Q 35. Soit

. Déterminer

pour

.
L'objectif de ces dernières questions est de déterminer

pour tous entiers

en établissant un lien entre ces valeurs et le modèle d'urne étudié dans cette partie.
On étudie un algorithme permettant de construire une permutation de

à partir d'une issue correspondant à

tirages.

On démarre la construction à la suite du premier tirage : on a nécessairement tiré la boule blanche et l'urne contient maintenant une boule de chaque couleur. On considère la suite ( ) qui comporte exactement une montée et une descente.
Si on tire la boule blanche (respectivement noire) lors du deuxième tirage, on insère la valeur 2 au milieu de la première et unique montée (respectivement descente) de la suite pour obtenir la suite ( ) (respectivement ).
Plus généralement, pour tout , si au -ième tirage on tire une boule blanche (respectivement noire) numérotée , on insère la valeur dans la suite au milieu de la ( )-ième montée (respectivement descente).
À la fin de la construction, on supprime les deux 0 de la liste (qui sont nécessairement restés en début et fin de liste). La liste obtenue contient les entiers de 1 à et représente un élément de . Si désigne la suite des tirages, on note la permutation obtenue.
À titre d'exemple, construisons .
Tirage 1:

On démarre avec la suite

Tirage 2:

L'entier

s'insère au milieu de la première (

) descente (la boule est noire) pour donner la nouvelle suite

Tirage

L'entier 3 s'insère au milieu de la deuxième montée pour donner (

).
On obtient ainsi

.
Q 36. À l'aide de l'algorithme ci-dessus, construire la permutation de

associée à l'issue (

).
Q 37. Réciproquement, soit

l'élément de

représenté par la suite (

). Déterminer une issue

comportant 7 tirages telle que

.
Q 38. À l'aide de la question 33, comparer, pour une issue quelconque, le nombre de boules blanches dans la composition finale de l'urne au nombre de montées de la permutation qui lui est associée par l'algorithme ci-dessus.
On admet que l'application

est bijective de

dans

et qu'elle induit une bijection entre l'évènement (

) et l'ensemble des permutations de

ayant

montées.
Q 39. Soit

. Déterminer, pour tout entier

et tout

le nombre

de permutations de

ayant

montées.