J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Centrale Physique Chimie 2 MPI 2025

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo centrale
🔗 Explorer
Banque
Centrale
Année
2025
Filière
MPI
Matière
Physique Chimie
Centrale MPICentrale 2025MPI Physique ChimiePhysique Chimie 2025
2025_09_04_93f9217bdce5aa8d1e06g

Une histoire de tubes

Le sujet comporte 3 parties relativement indépendantes, mais il est conseillé de les traiter dans l'ordre proposé.
Un formulaire et des données sont regroupés en fin d'énoncé.
Ce sujet a trait aux tubes à vide (figure 1a), longtemps utilisés pour construire des équipements électriques avant l'apparition des composants à base de matériaux semi-conducteurs. Les ordinateurs de la première génération des ordinateurs modernes étaient construits avec des tubes (environ 19000 pour l'ENIAC!). De nos jours, les tubes à vide sont encore utilisés dans certains équipements audio (figure 1b) et pour certaines applications de forte puissance. Les principaux inconvénients des tubes à vide sont leur encombrement, leur fragilité et la nécessité d'une tension d'alimentation élevée (quelques centaines de volts).
Aucune connaissance préalable sur les tubes à vide n'est requise pour traiter le questionnement.
Figure 1 - Tubes à vide.
Les tubes à vide sont classés selon le nombre d'électrodes qu'ils possèdent : diode (2 électrodes), triode (3 électrodes), tétrode (4 électrodes) et penthode (5 électrodes). La triode ECC83 (voir figure 1a) est le composant étudié dans ce sujet.
La figure 2 montre la constitution simplifiée d'une triode et le symbole électrique associé. Les électrodes de la triode s'appellent la cathode, l'anode et la grille. De plus, un filament dans lequel circule un courant continu chauffe la cathode. La présence de ce filament fait que ce tube est souvent nommé improprement lampe.
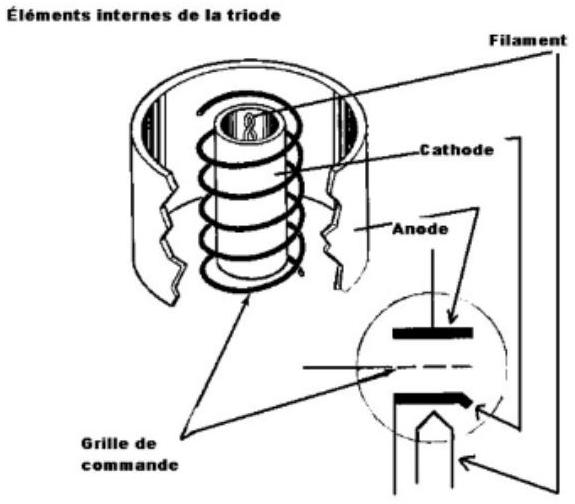
Figure 2 - Lien entre constitution et symbole électrique.
Source : Wikipédia.
Dans le tube de référence ECC83, la cathode est cylindrique de rayon et l'anode cylindrique de rayon . Elles sont coaxiales, d'axe ( ), et toutes deux de hauteur . L'ensemble est enfermé dans une enveloppe de verre et sous vide hors fonctionnement.

Partie A - La diode à vide

Dans cette première partie, la grille est ignorée. La triode ne fonctionne qu'avec sa cathode et son anode : il s'agit donc d'une diode. La cathode, chauffée par le filament (étudié partie B), est le siège d'une émission d'électrons appelée émission thermoïonique. Par hypothèse, ces électrons ne possèdent pas de vitesse initiale et leur nombre dépend de la température de la cathode. L'anode est portée au potentiel par rapport à la cathode de potentiel nul par choix ( ). Sous l'influence du champ électrique régnant entre cathode et anode, les électrons peuvent rejoindre l'anode et ainsi créer un courant électrique circulant depuis l'anode vers la cathode.

I - Caractéristique de la diode

Dans cette section, on cherche, en régime stationnaire, la caractéristique de la diode à vide, dont le symbole électrique est rappelé à la figure représente le courant anodique, fléché (positif) entrant par l'anode (et donc sortant par la cathode) et est la tension anode - cathode.
On note la densité volumique de charge électrique, a priori non uniforme, régnant dans l'espace entre anode et cathode et le potentiel électrostatique. On se place en coordonnées cylindriques ( ), l'axe ( ) étant confondu avec l'axe des cylindres anodique et cathodique.
Q1. Rappeler les équations de Maxwell en régime stationnaire. Justifier l'existence du potentiel électrostatique et établir la relation qui lie à . Donner le nom de cette relation.
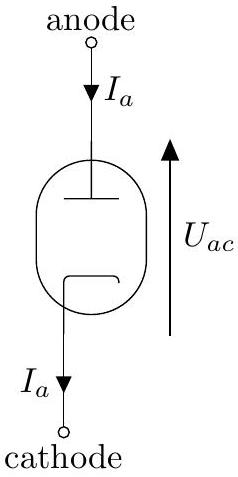
Les effets de bord sont négligés et on considère que le potentiel admet pour dépendance spatiale uniquement la coordonnée radiale .
Figure 3 - Diode à vide : symbole et fléchage des grandeurs électriques associées.
Q2. Proposer des éléments de justification de ces choix.
Q3. Évaluer, en ordre de grandeur, le poids d'un électron et la force électrostatique subie par un électron circulant depuis la cathode vers l'anode. Conclure.
Q4. Traduire la conservation de l'énergie mécanique d'un électron circulant depuis la cathode vers l'anode pour en déduire la vitesse d'un électron à la distance de l'axe en fonction, notamment, du potentiel électrique .
Q5. Rappeler l'équation locale de conservation de la charge en régime quelconque. En déduire, pour le régime stationnaire d'étude, une propriété vérifiée par le vecteur densité de courant électrique . Établir la relation qui existe en conséquence entre et le courant électrique anodique .
Q6. À l'aide des relations précédentes, montrer que le potentiel est solution de la relation suivante en précisant l'expression du facteur :
Q7. Vérifier la cohérence de l'unité du facteur .
L'équation différentielle obtenue à la question Q6 ne possède pas de solution analytique simple vérifiant les conditions aux limites imposées ici. Seule une solution approchée est recherchée dans le cadre de ce sujet.
Q8. Déterminer par quels facteurs sont multipliés et si le potentiel de l'anode est multiplié par un facteur .
Le résultat précédent et la forme du second membre de l'équation différentielle suggèrent une solution pour cette dernière sous la forme d'une loi puissance de type .
Q9. Déterminer le système d'équations dont et sont solutions. En déduire la valeur de et l'expression de en fonction de .
La forme de la solution utilisée ne permet pas de vérifier la condition imposée à la cathode : . On choisit d'adopter pour la suite la solution approchée qui vérifie cette condition, tout en conservant les expressions précédentes des constantes et .
Q10. Exprimer en fonction de et des autres paramètres utiles. En déduire que la relation caractéristique de la diode s'écrit et préciser l'expression de en fonction de , , et . Déterminer la valeur numérique de .
Q11. Expliquer pourquoi le résultat précédent n'est pas valable dans le cas . Préciser ce qu'il se passe dans ce cas et indiquer la valeur de correspondante.
Q12. Tracer la caractéristique .
On appelle «polariser une diode» l'action de choisir un point de fonctionnement pour celle-ci, c'est-à-dire choisir un couple de valeurs ( ) que l'on note ( ). Pour le tube ECC83, le point de fonctionnement optimal préconisé par le constructeur correspond à l'intensité .
Q13. Déterminer la valeur telle que .

II - Caractéristiques dynamiques de la diode

Q14. Pour , déterminer le temps de vol d'un électron entre la cathode et l'anode. En déduire, par analyse dimensionnelle, une expression et une estimation de la fréquence de coupure de la diode.
Si la tension varie légèrement de la quantité , cela engendre une légère variation de courant sur . Ces variations sont, à l'ordre 1 , proportionnelles entre elles et définissent la résistance dynamique de la diode .
Q15. Exprimer la résistance dynamique de la diode en fonction de et . Faire l'application numérique pour la valeur de .

III - Polarisation de la diode

Pour polariser le tube ECC83 au point de fonctionnement souhaité, d'intensité , un générateur de tension continue et une résistance sont utilisés comme illustré sur le circuit de la figure 4 (le circuit de chauffage de la cathode est non représenté). On admet à présent que la diode est caractérisée par la loi avec USI (unité du système international).
Q16. Écrire la relation entre et , appelée droite de charge, imposée dans la maille où la diode se trouve.
Q17. Déterminer la valeur de pour avoir .
Q18. Reproduire sur la copie la figure 5, puis y reporter la droite de charge de la question Q16, ainsi que la caractéristique de la diode. Ajouter également sur celle-ci les grandeurs précédemment introduites et (relative à ). Indiquer aussi la signification de la pente de la caractéristique de la diode au point de fonctionnement.
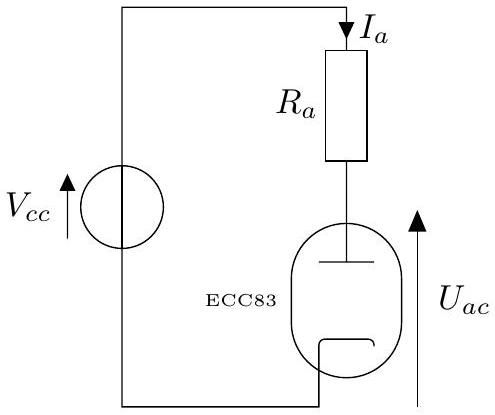
Figure 4 - Circuit de polarisation de la diode.
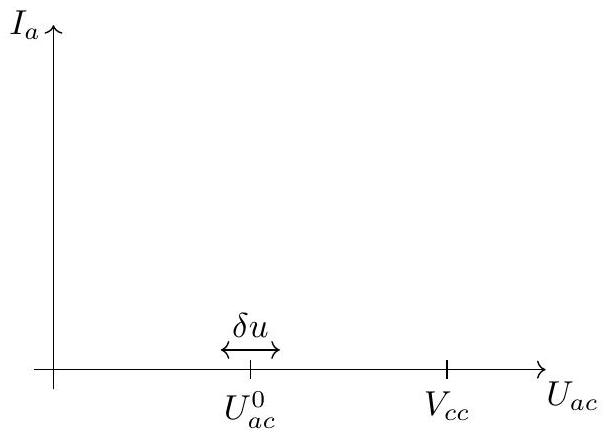
Figure 5 - Graphe schématique (pas à l'échelle) à reproduire et compléter.

Partie B - Température des éléments de la triode ECC83 et émission thermoïonique

I - Température du filament

Le filament qui chauffe la cathode, pour permettre une émission thermoïonique suffisante, est un fil de tungstène cylindrique homogène de longueur totale et de rayon , alimenté par une tension continue . Cette tension d'alimentation du filament est en pratique de ou 12 V selon les tubes, pour compenser le fait que la conductivité du tungstène, comme tous les métaux, diminue significativement avec la température ; cet effet est ignoré dans le cadre de ce sujet pour simplifier et on adopte pour la suite la valeur .
La conductivité électrique du tungstène est notée , sa masse volumique , sa capacité thermique massique et sa conductivité thermique .
Q19. Donner l'expression et calculer la résistance électrique du filament. En déduire la valeur de la puissance électrique é reçue par le filament.
Q20. Indiquer quels sont les différents modes de transfert thermique possibles. Préciser, avec justification, celui qui est mis en jeu lors du chauffage de la cathode par le filament.
On suppose que la loi de Stefan (ou de Stefan-Boltzmann) pour un corps noir s'applique à l'ensemble des éléments de la triode (filament, cathode et anode). La relation associée est avec la température de surface du corps et la constante de Stefan.
Q21. Rappeler quelle est la signification de la grandeur .
Q22. À l'aide d'un bilan énergétique entre et , établir l'équation différentielle régissant l'évolution temporelle de la température du filament (supposée uniforme). On pourra négliger le flux thermique reçu par le filament de la part du milieu extérieur.
Q23. En déduire l'expression et la valeur numérique de la température d'équilibre é du filament en régime stationnaire.
Q24. Évaluer l'ordre de grandeur du temps nécessaire pour que le filament atteigne la température é qui permet une émission thermoïonique stabilisée (les grandeurs et pourront être supposées indépendantes de la température pour l'évaluation de cet ordre de grandeur). Commenter dans le cadre d'un amplificateur audio à tubes (figure 1b).
Q25. Déterminer la couleur du filament lorsqu'il est chaud.

II - Température de la cathode et émission thermoïonique

La loi de Richardson donne la densité volumique de courant électrique émise par un métal en fonction de sa température :
Dans cette relation, est le travail de sortie, c'est-à-dire la barrière énergétique, de nature électrique, que doivent vaincre les électrons pour sortir du métal. La constante intervient dans une relation traduisant l'émission d'électrons (masse , charge ) via un processus microscopique non étudié ici.
Q26. Expliquer pourquoi la constante de Planck est susceptible d'intervenir dans l'expression de , en plus de et de la constante de Boltzmann .
Q27. Établir, à l'aide d'une analyse dimensionnelle, une expression de en fonction de et , à un facteur numérique sans dimension près (dont on admettra la valeur de ). Faire l'application numérique.
Dans la triode ECC83, la cathode et l'anode sont en nickel ( ). De plus, la cathode est recouverte d'une fine couche d'oxyde de baryum ( ) du coté anode. Ces valeurs sont supposées indépendantes de la température et on se place en régime stationnaire de fonctionnement.
Q28. En supposant que la cathode reçoit la totalité de la puissance émise par le filament, et en négligeant toute autre forme de transfert thermique reçu, déterminer la température de la cathode.
Q29. Calculer l'intensité électrique émise par la cathode côté filament et l'intensité électrique émise par la cathode côté anode. Comparer à l'intensité optimale de fonctionnement . Commenter.
Q30. Reprendre le tracé de la caractéristique de la question Q12 en tenant compte de ce qui précède et en justifiant.

Partie C - Amplificateur de tension à triode

Une troisième électrode, nommée grille, est ajoutée au dispositif décrit en partie A pour former une triode (voir figure 2). Il s'agit d'un nouveau filament conducteur entourant la cathode (à ne pas confondre avec le filament de chauffage). Ce filament est porté à une tension notée par rapport à la cathode, ce qui a pour conséquence de modifier le potentiel électrostatique régnant entre la cathode et l'anode; cela modifie aussi le courant anodique .
On note le courant de grille associé au flux d'électrons circulant depuis la cathode vers la grille. Le symbole de la triode et les grandeurs électriques associées sont illustrés sur la figure 6 .
Dans une triode, l'influence électrostatique de la grille est significativement plus importante que celle de l'anode. Par conséquent, le fonctionnement électrique de la triode est décrit par la relation avec, pour la triode ECC83, USI et ( ne dépend que de la géométrie du tube considéré et le facteur est différent de en raison de la prise en compte de la présence de la grille). Cette relation est vérifiée lorsque . On rappelle que seule la cathode est chauffée par le filament et donc seule la cathode est le
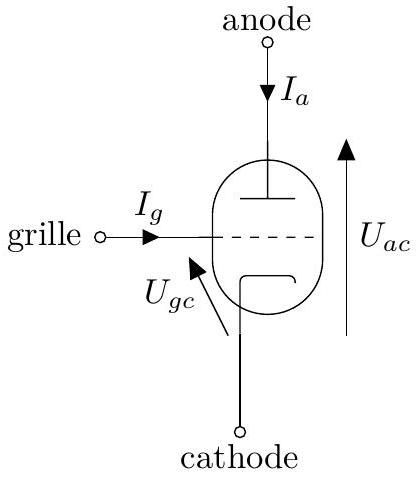
Figure 6 - Triode : symbole et fléchage des grandeurs électriques associées.
siège d'une émission significative d'électrons.

I - Montage amplificateur de tension à triode et principe d'analyse

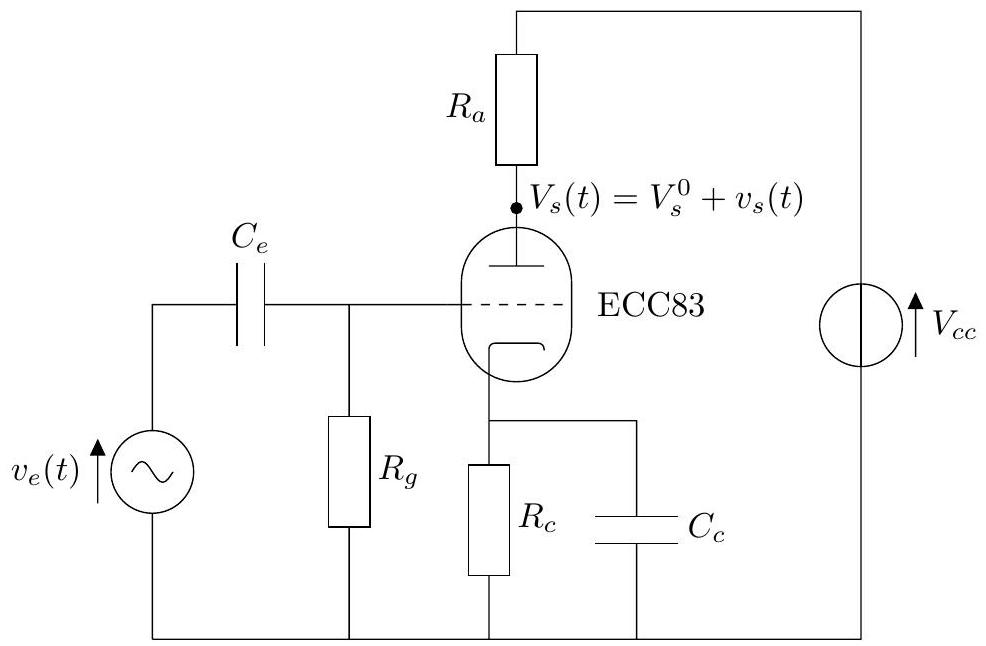
Une triode ECC83 est utilisée pour réaliser un amplificateur de tension selon le schéma de la figure 7. La tension à amplifier est la tension , variable, dont l'amplitude vaut quelques centaines de millivolts; elle est délivrée par un générateur idéal de tension et est de fréquence . La source de tension continue alimente le circuit, et permet de fixer le point de fonctionnement (ou point de polarisation) de la triode. Le signal de sortie est pris à l'anode du tube et comporte une composante continue notée et une composante variable notée , soit .
Figure 7 - Triode ECC83 utilisée en amplificateur de tension.
Q31. Donner une raison pour laquelle le principe de superposition ne s'applique pas dans ce circuit.
Les grandeurs électriques liées à la source peuvent être vues comme une perturbation à l'ordre 1 du point d'équilibre électrique dû à la source . Ainsi, l'analyse de ce circuit va être menée de la façon suivante :
  • étape 1 : étude, en régime stationnaire, du circuit sous la seule influence de , avec détermination du point de fonctionnement et de la triode ECC83, puis détermination de ;
  • étape 2 : linéarisation de la caractéristique de la triode, à l'ordre 1, autour du point de fonctionnement;
  • étape 3 : étude, en régime variable, du circuit linéarisé sous la seule influence de pour déterminer .
Q32. Donner un argument numérique justifiant cette démarche. Préciser de quelle(s) source(s) dépendent respectivement les grandeurs et .

II - Étape 1 : point de fonctionnement et dimensionnement des résistances et

Dans cette partie, seules les grandeurs continues sont prises en compte. La source est ainsi considérée, tandis que la source est supposée de tension nulle. À la mise sous tension, un régime transitoire apparait le temps de charger les différents condensateurs du montage. À l'issue de ce régime transitoire, le circuit est en régime stationnaire.
Q33. Déterminer le comportement électrique d'un condensateur en régime stationnaire. En déduire la représentation du schéma électrique équivalent du montage de la figure 7 en régime stationnaire.
Q34. Montrer alors qualitativement que quelles que soient les valeurs des résistances et .
Le point de fonctionnement souhaité est tel que et .
Q35. Déterminer la valeur de de compatible. En déduire les valeurs à prendre pour et . Expliquer pourquoi la valeur de n'intervient pas ici.
Q36. Préciser alors la valeur de .

III - Étape 2 : linéarisation du comportement de la triode ECC83

On s'intéresse maintenant aux petites variations autour du point de fonctionnement dues à la présence de . Les grandeurs électriques sont notées et avec et des infiniment petits d'ordre 1 devant respectivement et .
Q37. Donner un argument numérique autorisant à utiliser la caractéristique statique de la triode en régime variable.
Q38. Montrer que les grandeurs et sont liées à l'ordre 1 par la relation suivante, où les coefficients et sont à exprimer en fonction de et :
Q39. Exprimer la quantité . Commenter.
Q40. Calculer les valeurs numériques de et .

IV - Étape 3 : détermination du gain de l'amplificateur

Les condensateurs et sont supposés suffisamment capacitifs pour se comporter comme des fils (interrupteurs fermés) dans le domaine fréquentiel du signal . De plus, la source de tension étant une source continue, elle est aussi assimilable à un fil en régime variable car elle impose une variation de tension nulle à ses bornes. En se limitant aux signaux variables, le circuit électrique équivalent du montage amplificateur est donc celui de la figure 8 dans lequel les grandeurs et sont liées entre elles par la relation établie à la question Q38.
Q41. Montrer que et préciser l'expression de l'amplification en tension en fonction de et . Commenter le signe et calculer cette amplification en décimal et en décibels.
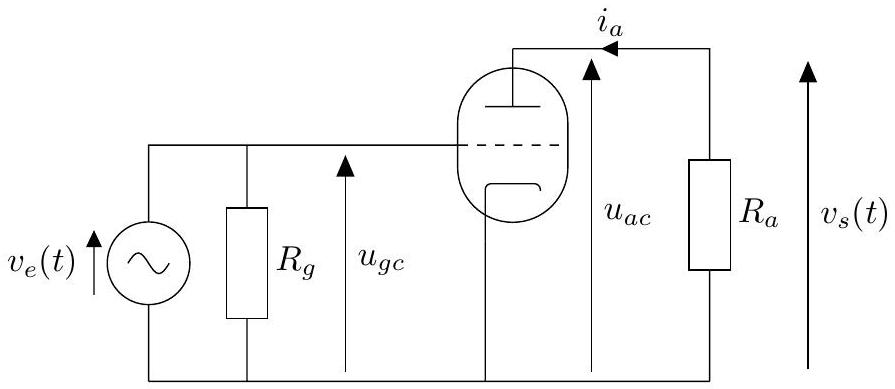
Q42. En réalité, la source n'est pas idéale et possède une résistance de sortie notée . Préciser, avec justification, comment doit être choisie la valeur de pour ne pas altérer la valeur de .
Figure 8 - Circuit équivalent en régime variable.

V - Distorsion harmonique de l'amplificateur

On cherche maintenant à quantifier la non-linéarité de l'amplificateur étudié en relation principalement avec la nonlinéarité de la caractéristique de la triode vis-à-vis de .
Q43. En reprenant le raisonnement effectué à la question Q38, mais à l'ordre 2 en , établir la relation :
Exprimer en fonction de et . Faire l'application numérique.
Q44. Déterminer alors l'expression de en fonction de et des autres grandeurs utiles.
Q45. Montrer que, pour un signal sinusoïdal de la forme , le signal comporte plusieurs composantes spectrales. Identifier leurs caractéristiques.
On appelle distorsion harmonique de rang , notée , le rapport de l'amplitude de l'harmonique de rang sur l'amplitude du fondamental. On exprime ce rapport en pourcentage.
Q46. Calculer les valeurs de pour et . Commenter.

Données et formulaire

Données numériques

Charge élémentaire
Masse de l'électron
Permittivité diélectrique du vide
Constante de Boltzmann
Constante de Planck
Constante de Stefan
Conductivité électrique du tungstène
Masse volumique du tungstène
Conductivité thermique du tungstène
Capacité thermique massique du tungstène

Formulaire

  • Loi de Wien : .
  • Pour un champ scalaire .
  • Pour un champ scalaire .
  • Pour un champ scalaire , à dépendance spatiale uniquement radiale en coordonnées cylindriques :
Centrale Physique Chimie 2 MPI 2025 - Version Web LaTeX | WikiPrépa | WikiPrépa