Version interactive avec LaTeX compilé

L'histoire du film The Martian (Seul sur Mars) de Ridley Scott, montre comment un homme, Mark Watney, survit seul sur Mars grâce à ses connaissances scientifiques. L'environnement hostile de la planète représente une contrainte de taille pour les ingénieurs et les scientifiques qui travaillent pour que des hommes puissent un jour poser le pied sur la planète rouge. La NASA annonce un vol habité pour Mars dans les années 2030, l'hypothèse du film n'est donc pas irréaliste. Même si cette histoire repose sur des travaux scientifiques et des techniques aérospatiales actuelles, on peut se demander si l'histoire est bien réaliste.
Certaines questions, repérées par une barre en marge, ne sont pas guidées et demandent de l'initiative de la part du candidat. Les pistes de recherche doivent être consignées, si elles sont pertinentes, elles seront valorisées. Le barème tient compte du temps nécessaire pour explorer ces pistes et élaborer un raisonnement.
Les quatre premières parties du sujet peuvent être liées notamment concernant les applications numériques. Les deux dernières parties sont indépendantes.
Toutes les données nécessaires à la résolution du sujet sont données en fin de sujet.
Certaines questions, repérées par une barre en marge, ne sont pas guidées et demandent de l'initiative de la part du candidat. Les pistes de recherche doivent être consignées, si elles sont pertinentes, elles seront valorisées. Le barème tient compte du temps nécessaire pour explorer ces pistes et élaborer un raisonnement.
Les quatre premières parties du sujet peuvent être liées notamment concernant les applications numériques. Les deux dernières parties sont indépendantes.
Toutes les données nécessaires à la résolution du sujet sont données en fin de sujet.
I La planète Mars
Mars est la quatrième planète par ordre de distance croissante au Soleil et la deuxième par masse et par taille croissantes sur les huit planètes que compte le système solaire. Dans le référentiel héliocentrique (aussi appelé référentiel de Kepler), supposé galiléen, la trajectoire de Mars est une ellipse contenue dans le plan de l'écliptique.
Extrait de CNRS Le journal
Question : Envoyer des humains sur Mars coûterait au moins 100 ou 200 milliards de dollars et ne serait possible que vers 2050 , à condition qu'une vraie volonté politique se dégage. Ne vaut-il pas mieux continuer à envoyer des robots?
Réponse du planétologue François Forget: C'est un vieux débat, [...] les robots ne sont pas forcément plus efficaces que les humains. Par exemple, un géologue peut repérer en quelques secondes une pierre intéressante, alors qu'il faudra des jours pour la repérer en manœuvrant un rover depuis la Terre, vu que les signaux radio mettent 5 à 22 minutes entre les deux planètes. Mais il y a une alternative qui me plaît bien: envoyer des humains en orbite martienne sans qu'ils se posent à la surface. Il est en effet très difficile - et donc coûteux de poser des charges de plus d'une tonne sur Mars. Parce que l'atmosphère y est trop fine pour freiner correctement avec un parachute comme sur Terre, et trop épaisse pour ralentir juste au-dessus de la surface avec de simples rétrofusées comme sur notre Lune. Autre avantage : plus besoin de MAV pour remonter, ni d'habitat en surface. Au final, depuis l'orbite, les astronautes pourraient facilement aller se poser sur les petites lunes Phobos ou Deimos (qui n'ont presque pas de gravité), et surtout piloter en quasi temps réel des robots sophistiqués envoyés sur Mars elle-même. Une telle mission pourrait avoir lieu dès 2035.
Réponse du planétologue François Forget: C'est un vieux débat, [...] les robots ne sont pas forcément plus efficaces que les humains. Par exemple, un géologue peut repérer en quelques secondes une pierre intéressante, alors qu'il faudra des jours pour la repérer en manœuvrant un rover depuis la Terre, vu que les signaux radio mettent 5 à 22 minutes entre les deux planètes. Mais il y a une alternative qui me plaît bien: envoyer des humains en orbite martienne sans qu'ils se posent à la surface. Il est en effet très difficile - et donc coûteux de poser des charges de plus d'une tonne sur Mars. Parce que l'atmosphère y est trop fine pour freiner correctement avec un parachute comme sur Terre, et trop épaisse pour ralentir juste au-dessus de la surface avec de simples rétrofusées comme sur notre Lune. Autre avantage : plus besoin de MAV pour remonter, ni d'habitat en surface. Au final, depuis l'orbite, les astronautes pourraient facilement aller se poser sur les petites lunes Phobos ou Deimos (qui n'ont presque pas de gravité), et surtout piloter en quasi temps réel des robots sophistiqués envoyés sur Mars elle-même. Une telle mission pourrait avoir lieu dès 2035.
09 novembre 2016
Q 1. En utilisant l'extrait du CNRS Le Journal, proposer un encadrement de la distance de Mars au Soleil. En déduire le demi-grand axe
Q 2. Sachant que la période de révolution de Mars est
Pour la suite, on prendra
Q 3. Déterminer la valeur du champ de pesanteur sur Mars.
Q 2. Sachant que la période de révolution de Mars est
Pour la suite, on prendra
Q 3. Déterminer la valeur du champ de pesanteur sur Mars.
II Tempête sur Mars
Lors d'une sortie sur Mars, l'écran de contrôle de Mark Watney est superposé à celui de l'action (figure 1). À gauche figurent les données externes et à droite celles concernant le scaphandre. Ainsi la pression extérieure vaut

Figure 1 Écran de contrôle de Mark Watney
II.A - L'atmosphère martienne
Q 4. Un bon scientifique pourra s'étonner du pourcentage de dioxygène dans le scaphandre. Quel est le problème?
Q 5. Estimer la masse volumique
Q 6. Tracer l'allure du diagramme
Q 7. Dans quel état se trouve l'eau sur Mars?
Q 8. Au cours d'une tempête martienne, la combinaison de Mark Watney est percée. Donner deux raisons pour lesquelles Mark Watney ne peut pas survivre dans ces conditions. (On supposera que le scaphandre se dépressurise en restant à température constante.)
Q 5. Estimer la masse volumique
Q 6. Tracer l'allure du diagramme
Q 7. Dans quel état se trouve l'eau sur Mars?
Q 8. Au cours d'une tempête martienne, la combinaison de Mark Watney est percée. Donner deux raisons pour lesquelles Mark Watney ne peut pas survivre dans ces conditions. (On supposera que le scaphandre se dépressurise en restant à température constante.)
II.B - Une tempête martienne peut-elle faire basculer le VAM?
Les coéquipiers de Mark Watney doivent faire décoller le VAM (Véhicule Ascensionnel Martien, figure 2) pris dans une tempête avant que celui-ci ne bascule et tombe sous la force du vent. Pour étudier le réalisme de la scène, on modélise le VAM (masse estimée : 10 tonnes) par un cylindre de diamètre
Q 9. Calculer le poids du VAM sur Mars.
Q 10. Évaluer la force de traînée s'exerçant sur le VAM pour un vent de
Q 11. Dans l'hypothèse où le VAM ne glisse pas, on le suppose «ancré » au point
Q 9. Calculer le poids du VAM sur Mars.
Q 10. Évaluer la force de traînée s'exerçant sur le VAM pour un vent de
Q 11. Dans l'hypothèse où le VAM ne glisse pas, on le suppose «ancré » au point
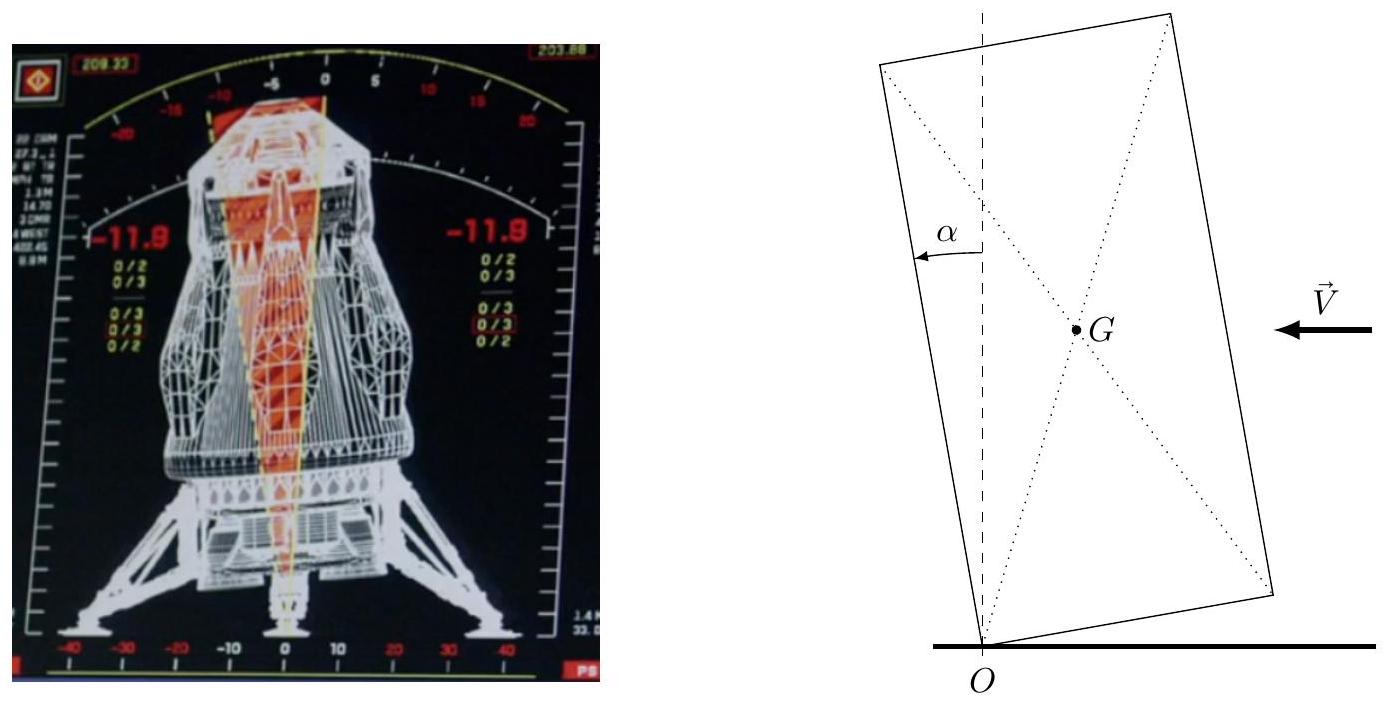
Figure 2 Basculement du VAM
III Dimensionnement des panneaux solaires
Étant donnés d'importants problèmes logistiques, les ingénieurs martiens envisagent des modules d'habitations cylindriques gonflables. En plus des problèmes liés à la différence de pression entre l'intérieur (à la pression terrestre) et l'extérieur, se pose également le problème du chauffage de ces modules. Dans la suite on considère que le chauffage est assuré par une pompe à chaleur (récepteur ditherme dont la finalité est de fournir de l'énergie à la source chaude) qui maintient une température interne de

Figure 3 Habitat et panneaux solaires
Q 12. Définir et déterminer l'efficacité maximale (efficacité de Carnot) d'une pompe à chaleur, en proposant une démonstration et une application numérique.
Q 13. Estimer la résistance thermique du module entre l'intérieur et l'extérieur, en admettant que le flux thermique est uniquement radial. On néglige les flux thermiques à travers les bases du cylindre.
Q 14. En admettant que la machine fonctionne avec une efficacité égale à
Q 15. L'énergie nécessaire pour alimenter le module en énergie provient de panneaux photovoltaïques dont le rendement de conversion est estimé à
Q 13. Estimer la résistance thermique du module entre l'intérieur et l'extérieur, en admettant que le flux thermique est uniquement radial. On néglige les flux thermiques à travers les bases du cylindre.
Q 14. En admettant que la machine fonctionne avec une efficacité égale à
Q 15. L'énergie nécessaire pour alimenter le module en énergie provient de panneaux photovoltaïques dont le rendement de conversion est estimé à
IV Sauvetage de Mark Watney par le vaisseau Hermès
Cette opération consiste à envoyer Mark Watney dans l'espace, grâce à un VAM, et à l'intercepter depuis le vaisseau Hermès «en plein vol », comme représenté figure 5. L'enjeu est donc que L'Hermès et Mark Watney se retrouvent au même endroit, au même moment avec une vitesse relative nulle.
IV.A - Trajectoire du vaisseau Hermès
Dans cette sous-partie, on se place dans le référentiel de Kepler.
Le vaisseau Hermès est utilisé pour les trajets Terre-Mars au cours desquels le vaisseau n'est soumis qu'à l'attraction du Soleil. L'orbite de transfert utilisée est une orbite de transfert de Hohmann : ellipse dont le périhélie est un point de l'orbite de la Terre et l'aphélie un point de l'orbite de Mars (figure 6). On supposera, pour simplifier, que les orbites de la Terre et de Mars sont circulaires de rayons respectifs
Le vaisseau Hermès est utilisé pour les trajets Terre-Mars au cours desquels le vaisseau n'est soumis qu'à l'attraction du Soleil. L'orbite de transfert utilisée est une orbite de transfert de Hohmann : ellipse dont le périhélie est un point de l'orbite de la Terre et l'aphélie un point de l'orbite de Mars (figure 6). On supposera, pour simplifier, que les orbites de la Terre et de Mars sont circulaires de rayons respectifs

Figure 4 Le vaisseau Hermès
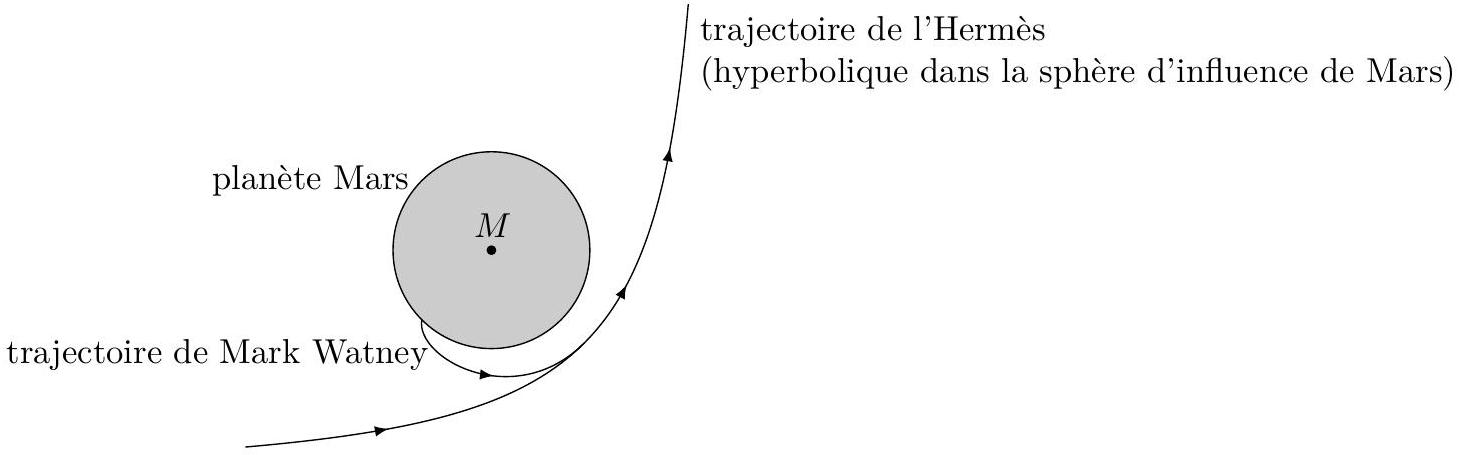
Figure 5 Principe de la récupération de Mark Watney
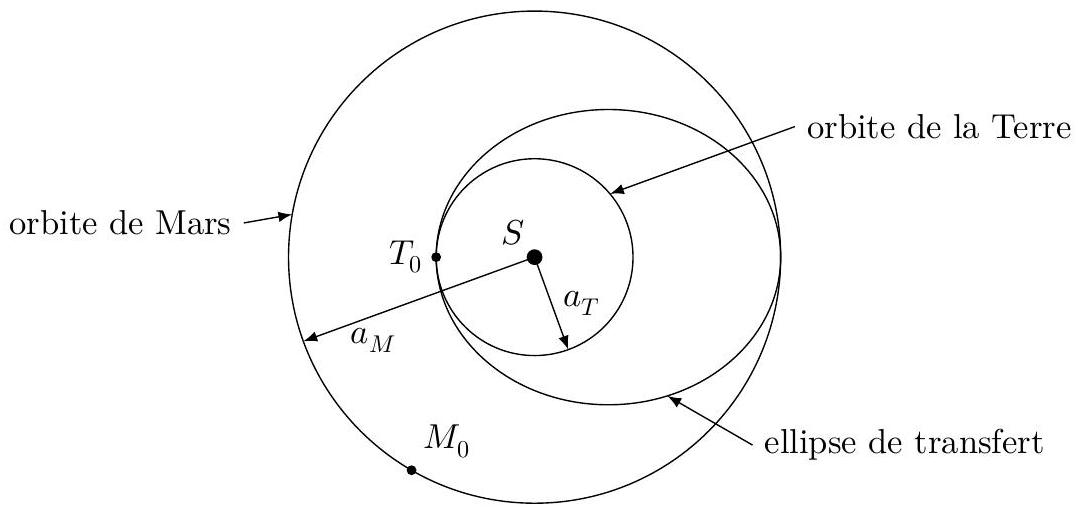
Figure 6
Q 16. Déterminer le demi grand axe
On considère le transfert du vaisseau de la Terre vers la planète Mars, les positions initiales de la Terre et de Mars étant notées respectivement
Q 17. Déterminer la durée du transfert. En déduire la position de Mars au moment du lancement sur Terre
Q 18. Montrer qu'un nouveau transfert, à partir de la Terre, ne peut avoir lieu qu'environ 780 jours après le premier lancement (période synodique).
Q 19. Une fois le vaisseau arrivé au voisinage de la planète Mars (
Q 20. Représenter les points
Q 21. En déduire qu'une mission aller-retour vers Mars dure au minimum 972 jours. Sachant qu'entre le départ de l'Hermès vers la Terre, suite à la tempête, et son retour sur Mars, il s'est écoulé 549 jours, commenter.
On considère le transfert du vaisseau de la Terre vers la planète Mars, les positions initiales de la Terre et de Mars étant notées respectivement
Q 17. Déterminer la durée du transfert. En déduire la position de Mars au moment du lancement sur Terre
Q 18. Montrer qu'un nouveau transfert, à partir de la Terre, ne peut avoir lieu qu'environ 780 jours après le premier lancement (période synodique).
Q 19. Une fois le vaisseau arrivé au voisinage de la planète Mars (
Q 20. Représenter les points
Q 21. En déduire qu'une mission aller-retour vers Mars dure au minimum 972 jours. Sachant qu'entre le départ de l'Hermès vers la Terre, suite à la tempête, et son retour sur Mars, il s'est écoulé 549 jours, commenter.
IV.B - La récupération de Mark Watney
Q 22. Au cours de l'opération de sauvetage, le vaisseau Hermès doit réduire brutalement sa vitesse de

Figure 7 Mark Watney se propulsant vers l'Hermès
Q 23. Au moment du sauvetage, Mark Watney s'aperçoit qu'il est encore trop loin de l'Hermès. il décide alors de percer sa combinaison (trou de diamètre de l'ordre de
V Fabrication d'eau sur Mars
Mark Watney est bien conscient que l'eau est l'une des clefs de sa survie sur Mars. Il n'en manque pas grâce à l'ingéniosité des procédés développés dans le domaine spatial mais il a besoin d'énormes quantités d'eau pour arroser ses plants de pomme de terre et assurer son alimentation en attendant l'aide hypothétique de la Terre. Heureusement, outre sa qualité de botaniste, il a des notions élémentaires de mécanique, de physique et de chimie.
Mark Watney estime avoir besoin de 600 L d'eau, qu'il décide d'obtenir par combustion de dihydrogène par le dioxygène. Il peut obtenir le dihydrogène par décomposition de l'hydrazine et le dioxygène par réduction du
L'hydrazine dont il souhaite tirer le dihydrogène avant de le «brûler » pour former l'eau est un carburant notamment utilisé dans la conquête spatiale. Les réactions chimiques de décomposition de l'hydrazine en molécules de
Mark Watney estime avoir besoin de 600 L d'eau, qu'il décide d'obtenir par combustion de dihydrogène par le dioxygène. Il peut obtenir le dihydrogène par décomposition de l'hydrazine et le dioxygène par réduction du
L'hydrazine dont il souhaite tirer le dihydrogène avant de le «brûler » pour former l'eau est un carburant notamment utilisé dans la conquête spatiale. Les réactions chimiques de décomposition de l'hydrazine en molécules de
Q 24. Proposer des formules de Lewis pour l'hydrazine
Q 25. Déterminer le volume d'hydrazine (densité 1,02 ) nécessaire pour obtenir les 600 L d'eau liquide voulus par Mark Watney.
Q 26. La présence du catalyseur d'iridium modifie-t-elle l'état d'équilibre?
Q 27. L'iridium cristallise dans un réseau cubique à faces centrées avec une densité de 22,5 . Représenter cette maille cristalline. Estimer le rayon atomique de l'iridium.
Q 28. Calculer la constante thermodynamique de la réaction
Q 29. Comment évolue la réaction
Q 30. Quelle est la température maximale atteinte lors de la combustion du dihydrogène ?
Q 25. Déterminer le volume d'hydrazine (densité 1,02 ) nécessaire pour obtenir les 600 L d'eau liquide voulus par Mark Watney.
Q 26. La présence du catalyseur d'iridium modifie-t-elle l'état d'équilibre?
Q 27. L'iridium cristallise dans un réseau cubique à faces centrées avec une densité de 22,5 . Représenter cette maille cristalline. Estimer le rayon atomique de l'iridium.
Q 28. Calculer la constante thermodynamique de la réaction
Q 29. Comment évolue la réaction
Q 30. Quelle est la température maximale atteinte lors de la combustion du dihydrogène ?
VI Peut-on cultiver des pommes de terre sur Mars?
Pour s'alimenter Mark Watney fait pousser des pommes de terre dans le sol martien en utilisant les selles récupérées dans les toilettes de la mission. Les selles contiennent des bactéries nécessaires à une culture. Néanmoins, les sondes Viking ont montré qu'un tel sol, particulièrement oxydant, tue toutes les bactéries, à fortiori celles des selles. Dans cette partie, afin d'étudier l'action oxydante du sol sur les bactérie on utilise la bactérie
VI.A - Métabolisme de la bactérie
Le peroxyde d'hydrogène est un sous-produit du métabolisme des cellules, sa production suit une cinétique d'ordre 0 de constante de vitesse
VI.A.1) La bactérie est modélisée par une sphère de volume total
Dans l'hypothèse d'un régime stationnaire, on définit une résistance particulaire
VI.A.1) La bactérie est modélisée par une sphère de volume total
Dans l'hypothèse d'un régime stationnaire, on définit une résistance particulaire
où
Q 31. Citer deux autres domaines de la physique utilisant la notion de résistance. Préciser les analogies.
Q 32. Exprimer
Q 33. Simplifier cette expression dans l'hypothèse où
Q 34. Proposer une valeur numérique de
Q 35. Montrer que la loi de cinétique de diffusion à travers la membrane peut s'écrire sous la forme
Q 31. Citer deux autres domaines de la physique utilisant la notion de résistance. Préciser les analogies.
Q 32. Exprimer
Q 33. Simplifier cette expression dans l'hypothèse où
Q 34. Proposer une valeur numérique de
Q 35. Montrer que la loi de cinétique de diffusion à travers la membrane peut s'écrire sous la forme
Q 36. Quel signe doit-on choisir sachant que
VI.A.2) Les enzymes présentes dans la bactérie obéissent à une cinétique, dite michaelienne, où la vitesse de réaction a la forme générale
VI.A.2) Les enzymes présentes dans la bactérie obéissent à une cinétique, dite michaelienne, où la vitesse de réaction a la forme générale
où
Q 37. Quelle est la dimension de la constante
VI.A.3) La dynamique du peroxyde d'hydrogène est donc décrite par le système présenté figure 8.
Q 37. Quelle est la dimension de la constante
VI.A.3) La dynamique du peroxyde d'hydrogène est donc décrite par le système présenté figure 8.
| Réactions associées à
|
Équations chimiques | Loi de vitesse |
| Production métabolique |
|
ordre 0 |
| Décomposition par Ahp |
|
|
| Décomposition par Cat |
|
|
| Diffusion membranaire |
|
|
Figure 8
On note
Q 38. Préciser les degrés d'oxydation de l'oxygène dans les trois molécules de la réaction
Q 38. Préciser les degrés d'oxydation de l'oxygène dans les trois molécules de la réaction
Q 39. Calculer la constante thermodynamique de cette réaction de décomposition à
Q 40. Donner les équations différentielles associées au système dynamique ci-dessus vérifiées par
En condition physiologique, sans stress exogène, on admet que
Q 41. Déterminer la concentration en peroxyde d'hydrogène à l'équilibre à l'intérieur des cellules.
Q 42. Faire l'application numérique, commenter.
Q 40. Donner les équations différentielles associées au système dynamique ci-dessus vérifiées par
En condition physiologique, sans stress exogène, on admet que
Q 41. Déterminer la concentration en peroxyde d'hydrogène à l'équilibre à l'intérieur des cellules.
Q 42. Faire l'application numérique, commenter.
VI.B - Situation de stress oxydant
On considère désormais une situation de stress oxydant produit par l'ajout d'une importante quantité de peroxyde d'hydrogène exogène (c'est-à-dire introduite à l'extérieur de la bactérie) : on suppose que les bactéries se trouvent dans un milieu où la concentration extérieure en peroxyde d'hydrogène vaut initialement
Q 43. Proposer une approximation à l'équation différentielle vérifiée par
Q 44. En déduire la quantité (en mole) de peroxyde d'hydrogène décomposé par seconde et par bactérie.
Q 45. Combien de temps faudra-t-il à
Q 43. Proposer une approximation à l'équation différentielle vérifiée par
Q 44. En déduire la quantité (en mole) de peroxyde d'hydrogène décomposé par seconde et par bactérie.
Q 45. Combien de temps faudra-t-il à
Données
Terre-Mars
| Terre | Mars | |
| Composition de l'atmosphère |
|
|
| Rayon des planètes
|
6380 | 3390 |
| Densité globale | 5,5 | 3,9 |
Grandeurs thermodynamiques entre
|
|
|
|
|
|
|
| Enthalpie standard de formation
|
-394 | -111 | -242 | ||
| Entropie standard molaire
|
214 | 237 | 198 | 130 | 189 |
| Capacité thermique molaire
|
49,0 | 34,0 | 32,0 | 30,0 | 37,0 |
Au sujet de E. coli
| Notation | Valeurs | |
| Production de
|
|
|
| Constante de Michaelis pour Catalase |
|
|
| Constante de Michaelis pour Ahp |
|
|
| Vitesse maximale pour Catalase |
|
|
| Vitesse maximale pour Ahp |
|
|
| Coefficient de diffusion membranaire pour
|
|
|
| Volume d'une bactérie |
|
|
| Épaisseur de la paroi |
|
9 nm |
| Constante gravitationnelle |
|
| Célérité de la lumière |
|
| Constante d'Avogadro |
|
| Constante des gaz parfaits |
|
| Masses molaires (
|
|
| Viscosité du
|
|
| Viscosité de l'air terrestre (à
|
|
| Distance Terre-Soleil |
|
| Température de la surface du Soleil |
|
| Rayon du Soleil |
|
| Masse du vaisseau Hermès |
|
Pression de vapeur saturante de l'eau en fonction de la température
|
|
|
|
|
|
|
|
|
| -75 | 0,122 | -40 | 12,84 | 0 | 611,15 | 35 | 5626,7 |
| -70 | 0,261 | -35 | 27,71 | 5 | 872,60 | 40 | 7381,4 |
| -65 | 0,540 | -30 | 38,01 | 10 | 1228,1 | 45 | 9589,8 |
| -60 | 1,080 | -25 | 63,29 | 15 | 1705,6 | 50 | 12344 |
| -55 | 2,093 | -20 | 103,26 | 20 | 2338,8 | 55 | 15752 |
| -50 | 3,936 | -15 | 165,30 | 25 | 3169,0 | 60 | 19932 |
| -45 | 7,202 | -10 | 259,90 | 30 | 4245,5 | 65 | 25022 |
d'après CRC Handbook of Chemistry and Physics - 2004
Coefficient de traînée
Le graphe donné figure 9 représente l'évolution du coefficient de traînée d'un cylindre de diamètre
Coefficient de traînée
Le graphe donné figure 9 représente l'évolution du coefficient de traînée d'un cylindre de diamètre
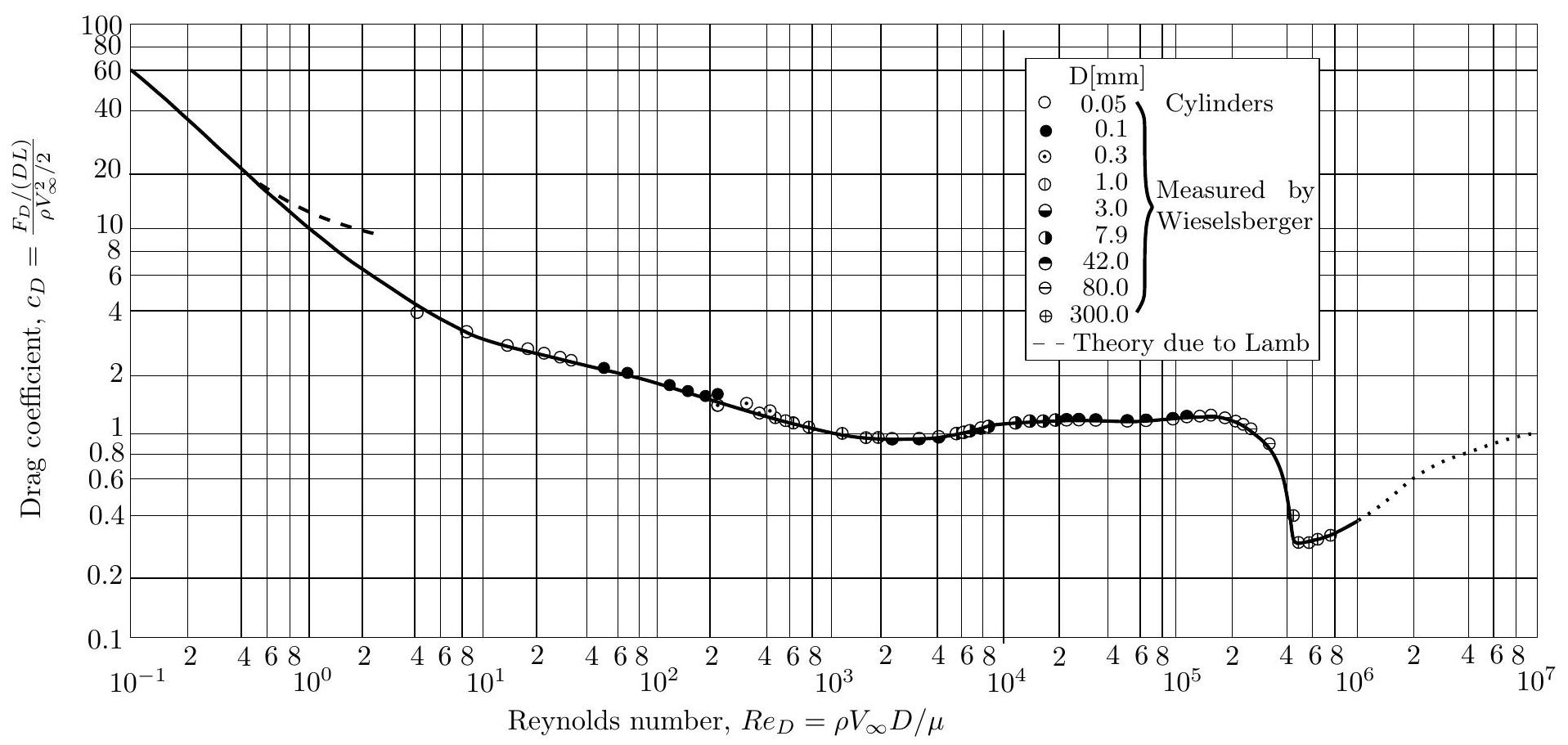
Figure 9 Coefficient de trainée en fonction du nombre de Reynolds
