siècle. Ce problème se propose d'aborder différents aspects du fonctionnement et de la conception de l'instrument. Les différentes parties sont largement indépendantes.

I Vibrations d'une corde de piano fixée à ses deux extrémités

Lorsque l'instrumentiste frappe une touche du clavier, celle-ci actionne un mécanisme, qui actionne à son tour un marteau

, qui vient frapper une corde

. Celle-ci entre alors en vibration libre (tant que la touche est enfoncée). On s'intéresse donc dans cette partie aux vibrations libres d'une corde du piano.
Sauf avis contraire, on supposera que la corde peut être supposée sans raideur et on négligera toujours les effets de la pesanteur.
La corde de masse linéique

est tendue avec la tension

. Au repos, la corde est rectiligne et parallèle à l'axe horizontal (

). On étudie les mouvements de la corde autour de sa position d'équilibre. On note

le déplacement du point de la corde à l'abscisse

à l'instant

. L'axe (

) est l'axe vertical ascendant.

I.A - Mise en équation du mouvement transversal d'une corde de piano sans raideur

I.A.1) Que signifie l'expression «corde sans raideur»? Qu'entend-on par «hypothèse des petits mouvements »?
I.A.2) Dans le cadre de l'approximation des petits mouvements, établir les deux équations liant les dérivées partielles par rapport à

et à

de la vitesse transversale d'un point de la corde

et de la projection sur l'axe (

) de la force de tension exercée à l'abscisse

par le morceau de corde situé à droite de cette abscisse sur la partie située à gauche

. On fera apparaitre la tension

en le justifiant.
I.A.3) Montrer que la fonction

vérifie l'équation aux dérivées partielles

Identifier la célérité

des ondes transversales sur la corde et en donner l'expression. Comment s'appelle cette équation ? Citer au moins deux autres phénomènes régis par la même équation.
I.A.4) On peut lire dans une documentation technique que «une corde de piano est tendue à 85 kg ». Pouvez-vous en déduire un ordre de grandeur de la tension

d'une corde ? Pour une corde en acier donnant la note «La 4 », le diamètre de la corde est de

. La masse volumique de l'acier valant

, calculer la célérité

des ondes transversales sur la corde.

I.B - Modes propres d'une corde de piano sans raideur, fixée aux deux extrémités. Position du marteau sur la corde

La corde est fixée à ses deux extrémités,

, ce qui impose les conditions aux limites :

.
I.B.1) Qu'appelle-t-on onde stationnaire? Montrer que les solutions en ondes stationnaires, physiquement acceptables, de l'équation (I.1) sont de la forme

. Quelle est la relation entre

?
I.B.2) Qu'appelle-t-on «modes propres» et «fréquences propres» de la corde ? Exprimer les fréquences propres

de la corde en fonction de

. Donner l'expression de la solution

correspondant au mode propre numéro

. Dessiner l'aspect de la corde à plusieurs instants bien choisis pour

I.B.3) La solution générale de l'équation (I.1) correspondant aux conditions aux limites

est une superposition des modes propres, qui s'écrit

La corde est frappée à l'instant initial par un marteau de largeur

(faible), situé à l'abscisse

(pendant un intervalle de temps supposé infiniment court). Ce marteau communique une vitesse initiale transversale à la corde. On se donne les conditions initiales suivantes (juste après l'attaque de la corde par le marteau) en tout point de la corde:

la forme initiale de la corde donnée par ;
la vitesse initiale de la corde donnée par

a) On donne le résultat du calcul :

Quel est l'effet de la largeur

du marteau? Pour une corde de piano de longueur

( «Do 4 », fréquence fondamentale

), donner l'ordre de grandeur de la fréquence au-delà de laquelle cet effet est sensible. La largeur du marteau vaut

. Commentaire?
b) Comment choisir le point d'attaque si l'on veut supprimer l'harmonique de rang

I.C - Conséquences sur la conception des cordes d'un piano

La hauteur du son produit par une corde est fixée par la fréquence

de son mode fondamental

. Les 88 notes d'un piano moderne s'échelonnent du «La 0 » (fréquence fondamentale

) au «Do 8 » (fréquence fondamentale

).
I.C.1) Rappeler la relation liant la longueur

d'une corde à la fréquence de son fondamental

On rappelle que pour la fréquence fondamentale

, on a une longueur de corde

. Quelles sont les valeurs extrêmes des longueurs de corde prévues dans l'extrême grave et dans l'extrême aigu?
I.C.2) Les longueurs calculées ci-dessus sont excessives dans le grave (problèmes d'encombrement et de fragilisation de la structure à cette échelle) : en pratique, la longueur d'un piano à queue de concert moderne n'excède pas 3 m (la longueur la plus courante étant autour de

). La longueur des cordes obéit assez bien à la loi étudiée au I.C. 1 pour les notes au-delà du «Do 4 ». Pour les notes plus graves, on utilise des cordes filées : il s'agit de cordes d'acier, autour desquelles on a enroulé un fil de cuivre. La longueur de corde variant peu dans ce domaine du clavier, expliquer l'intérêt de ce procédé. Pourrait-on envisager de jouer sur la tension

des cordes?
I.C.3) On donne la masse volumique du cuivre:

. En assimilant l'enroulement de cuivre à une couche homogène d'épaisseur 1 mm recouvrant le cœur d'acier de diamètre

, et pour la tension

, calculer la longueur de la corde du «La 0 » (note la plus grave du piano, de fréquence fondamentale

I.D - Prise en compte de la raideur : dispersion et inharmonicité

En réalité, à cause de l'élasticité du matériau constituant une corde, il faut prendre en compte sa raideur. Cela est particulièrement vrai pour les cordes de grand diamètre

. Il nous faut donc raffiner le modèle adopté jusqu'à présent. On considère toujours que les mouvements de la corde sont transversaux, et contenus dans le plan vertical

. La théorie de l'élasticité montre que la tension

n'est plus tangente à la corde et que pour permettre la courbure de la corde, il faut prendre en compte un couple de moment

dont l'expression est donnée par

où

désigne le rayon de la corde.

, appelé «module d'Young», traduit les propriétés d'élasticité du matériau constituant la corde et s'exprime en Pascal. On considère ici une corde en acier de masse volumique

acier

et de module d'Young

La portion de corde comprise entre les abscisses

est donc soumise aux forces de tension et aux couples

I.D.1)

a) Vérifier l'homogénéité de la relation donnant

.
b) En appliquant le théorème de la résultante cinétique à la portion

, montrer que

ne dépend que du temps. On supposera que

est en réalité une constante notée

. Établir également une équation aux dérivées partielles liant

.
c) En appliquant le théorème du moment cinétique barycentrique à la portion

, établir une nouvelle équation aux dérivées partielles liant

. À cette fin, on négligera en justifiant cette approximation le moment d'inertie de la portion

par rapport à l'axe

.
d) En déduire l'équation aux dérivées partielles régissant les mouvements de la corde

où

désigne toujours la masse linéique de la corde.
I.D.2) On s'intéresse à l'influence de la raideur sur les fréquences propres de la corde. On se place donc dans un mode propre de vibration et on suppose

.
a) Établir la relation de dispersion

d'un tel mode.
b) Montrer que les fréquences propres de la corde tendue entre ses extrémités fixées en

s'écrivent

où

est un entier naturel non nul,

la célérité des ondes sur la corde sans raideur et

une constante qu'on exprimera en fonction de

. Pouvez-vous en déduire un des avantages présentés par un piano à queue par rapport à un piano droit ?
c) Tracer sur un même graphique les courbes représentatives de

en fonction de

pour une corde sans raideur et pour la même corde avec raideur. Commenter.
d) Calculer numériquement

(on prendra

). En déduire l'expression approchée de l'inharmonicité de raideur

, définie par le rapport

où

désigne la fréquence propre du mode

pour une corde sans raideur.
e) À partir de quel rang

la fréquence propre

de la corde avec raideur est-elle plus élevée d'un demi-ton que celle de la corde idéale,

? Donnée : deux notes séparées d'un demi-ton ont des fréquences fondamentales qui sont dans un rapport

II Couplage entre une corde de piano et la table d'harmonie: le rôle du chevalet

On revient ici à une corde sans raideur.
Une corde vibrante est un «radiateur» acoustique très peu efficace. Si l'on veut produire du son efficacement, il faut utiliser une structure de bien plus grande taille : il s'agit de la table d'harmonie, mince planche d'épicéa, qui par ses vibrations, rayonne du son dans l'espace environnant. On s'intéresse à la manière dont la corde vibrante peut transférer une partie de son énergie à la table d'harmonie par l'intermédiaire d'une pièce de bois collée sur la table: le chevalet.

II.A - Impédance caractéristique d'une corde vibrante

II.A.1) On considère une onde progressive sinusoïdale se propageant vers les

croissants le long de la corde sans raideur étudiée dans la partie I.A. On conserve les notations de la partie I. Montrer que pour cette onde progressive, le rapport

est constant et prend la valeur

. On appelle «impédance caractéristique » de la corde la grandeur

. Quelle est la dimension de

?
II.A.2) Que devient ce rapport si l'onde progressive sinusoïdale se propage vers les

décroissants ?

II.B - Couplage corde-chevalet

La «partie utile» (ou longueur vibrante) de la corde est tendue entre l'extrémité gauche (en

) où l'agrafe la maintient immobile :

, et l'extrémité droite (en

) où elle repose sur le chevalet.

Figure 1

II.B.1) On propose de modéliser l'extrémité droite de la corde (située en

) par la condition aux limites

, où

est une constante positive caractérisant le couplage corde-chevalet. Cette constante

se nomme l'impédance mécanique de l'ensemble chevalet-table d'harmonie. Pourquoi ce modèle est-il pertinent selon vous? De quel phénomène rend-il compte ? On se contentera d'une réponse qualitative.
II.B.2) On cherche des solutions en ondes stationnaires de la forme

où

est un nombre complexe. Montrer que

et que

où l'on a posé

. Ce dernier résultat peut se récrire

forme que l'on adopte dorénavant.
II.B.3)

étant complexe, on pose

, où

sont des réels et

. Dans le cas où

, qui correspond au cas du piano, calculer les valeurs possibles de

; commenter. Calculer également

en fonction de

commenter.
II.B.4) Montrer que la solution précédente tenant compte du couplage avec le chevalet est de la forme

. Qu'en dites-vous ? Est-ce toujours une onde stationnaire ?
II.B.5) L'expérience quotidienne du pianiste montre qu'une note peut persister plusieurs secondes dans l'extrême grave, tandis que dans l'extrême aigu, le son ne persiste qu'une fraction de seconde. Les calculs menés ci-dessus sont-ils en accord avec l'expérience? Quel(s) raffinement(s) pourrait-on apporter au modèle ?

III Corrosion des cordes de piano

Les cordes de piano sont en acier extrêmement solide et sont de diamètre variable, d'environ

pour les notes les plus aiguës jusqu'à

pour les notes les plus graves. Les cordes de grave sont dites filées dans la mesure où elles sont gainées d'un fil de cuivre destiné à les alourdir pour permettre une tension moindre et une plus grande flexibilité.
Chacune des trois sous-parties est indépendante et peut être traitée séparément des autres.

III.A - L'acier : constituant essentiel des cordes de piano

L'acier est constitué d'au moins deux éléments, majoritairement le fer puis le carbone dans des proportions comprises entre

en masse. C'est essentiellement la teneur en carbone qui confère à l'alliage les propriétés du métal qu'on appelle «acier». La structure du fer + carbone évolue d'une façon complexe en fonction de la température et de la teneur en carbone.

III.A.1) Le fer

Le fer peut cristalliser sous deux formes selon la température. À basse température, le fer

cristallise dans une structure cubique centrée cc.
a) Donner la définition d'une maille élémentaire.
b) Combien la maille conventionnelle du fer

contient-elle d'atomes de fer ?
c) On donne le paramètre de la maille cubique

. Calculer alors le rayon atomique du fer

ainsi que la masse volumique du fer

.
d) Dans la représentation de la maille de fer

donnée figure 2 , à quel type de site intersticiel correspond

? Est-il régulier ? Justifier votre réponse.
e) Répondre aux mêmes questions pour le site intersticiel

, situé à la distance

.
f) Localiser et dénombrer les deux types de sites dans la maille conventionnelle du fer

.
g) Établir en fonction de

l'expression de

, rayon maximal d'un atome qui s'insèrerait dans un site

sans déformation de la structure cristalline de base. Calculer

.
h) Répondre à la même question pour le site

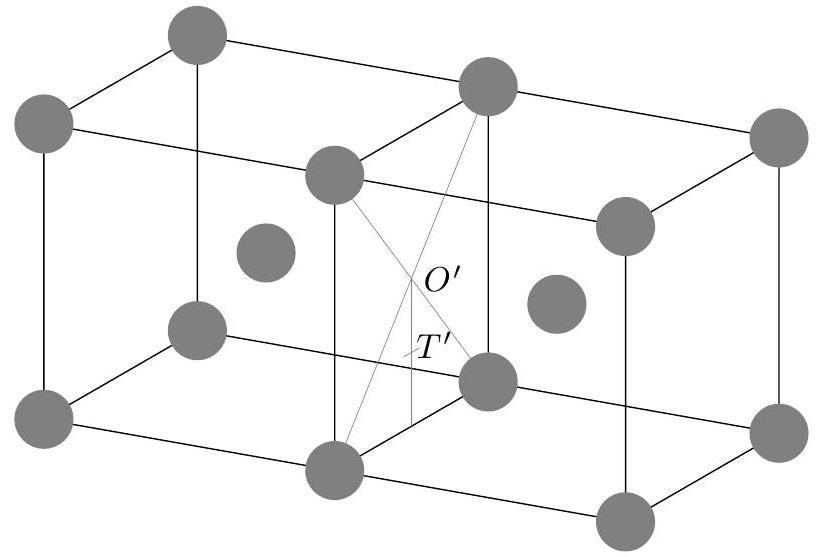
Figure 2 Sites intersticiels

dans la maille de fer

III.A.2) Du fer à la ferrite

La ferrite est une solution solide de carbone dans le fer

. Le terme ferrite désigne en effet l'acier à très faible teneur en carbone.
a) Indiquer dans quel type de site interstitiel les atomes de carbone se placeront afin d'engendrer le minimum de déformation du réseau hôte. Est-il possible que cela se fasse sans aucune déformation?
b) Le maximum de «solubilité» du carbone est de

en masse. Établir la formule de la ferrite

.
c) Déterminer le pourcentage d'occupation des sites

par les atomes de carbone.
d) Calculer la masse volumique de la ferrite en supposant que le réseau hôte n'est pas déformé.

III.B - Cordes de grave

Intéressons-nous maintenant au cuivre : l'élément ainsi que sa préparation industrielle pour les cordes de piano.

III.B.1) Le cuivre: configuration électronique, isotopes stables

a) Donner la configuration électronique attendue du cuivre dans son état fondamental en énonçant les règles utilisées. Préciser quels sont les électrons de cœur et ceux de valence.
En réalité, cet élément constitue une exception à la règle de Klechkowski, sa configuration ne laisse apparaitre qu'un seul électron de valence. Donner cette configuration et proposer une explication.
b) Donner la définition d'un élément de transition et situer avec précision ces éléments dans la classification périodique. Déduire de la configuration électronique attendue déterminée à la question III.B.1.a, la place de l'élément cuivre dans la classification périodique.

III.B.2) Préparation industrielle du cuivre

Le cuivre est un des rares métaux qui existent à l'état natif. Ce fait d'ailleurs explique probablement qu'il fut le premier métal utilisé par les hommes. Les minerais de cuivre sont essentiellement constitués de sulfures avec de nombreuses impuretés métalliques. La métallurgie du cuivre est réalisée selon deux procédés différents :

le procédé par voie sèche,
le procédé par voie humide.
a) Comment nomme-t-on ces deux types de métallurgie ?

La voie humide pour l'extraction du cuivre est de plus en plus privilégiée. Celle-ci comporte schématiquement trois étapes:

la lixiviation,
la cémentation,
l'électrolyse.
b) Expliciter les termes de lixiviation et de cémentation.

La solution de sulfate de cuivre

et d'acide sulfurique obtenue après les deux premières opérations subit une électrolyse.
La figure A du document réponse fournit la courbe intensité-potentiel pour une électrode de cuivre au contact d'une solution molaire d'acide sulfurique (courbe

) et celle obtenue avec la même électrode au contact d'une solution molaire de sulfate de cuivre (courbe

).
c) Décrire le montage expérimental à effectuer pour tracer une courbe intensité-potentiel.
d) Préciser les réactions électrochimiques mises en jeu dans les deux parties des deux courbes (écrire directement sur le document réponse qui sera à rendre avec la copie).
Rappel: en solution, les ions hydrogénosulfate

et sulfate

ne sont pas électroactifs pour la réduction.
e) Comment peut-on qualifier le couple

à la réduction? À l'oxydation ?
f) Si l'on augmente la tension, on voit apparaître un palier sur l'une des branches de la courbe

. Compléter qualitativement le diagramme et expliquer l'origine de ce palier. De quoi dépend son ordonnée ? Pour quel type de réactions électrochimiques ce palier n'est-il pas observé ?
La solution molaire de sulfate de cuivre et d'acide sulfurique (

) est électrolysée dans une cuve, avec une anode en plomb passivé, sur laquelle il y a dégagement de dioxygène et une cathode en cuivre très pur sur laquelle le cuivre se dépose. La figure 3 présente la courbe intensité-potentiel enregistrée.

Figure 3

g) Quelles sont les réactions qui ont lieu aux électrodes ? (les propriétés redox du plomb n'interviennent pas). Pour qu'il y ait réaction à l'électrode, il est nécessaire que les espèces électroactives s'approchent de cette électrode. Quels sont les trois phénomènes qui assurent le transport de matière ?
h) Déterminer la tension théorique de fonctionnement

(on admettra que les gaz se dégagent sous la pression atmosphérique).
En réalité, pour une densité de courant de

, compte tenu des phénomènes de surtension et de chute ohmique dans l'électrolyseur, la tension à appliquer est de

.
Sachant que le rendement faradique est de

, déterminer l'énergie nécessaire pour déposer 1 kg de cuivre pur.

III.C - Corrosion de l'acier à l'air humide

Dans l'acier ordinaire, la présence de carbone améliore beaucoup les propriétés mécaniques du fer sans pour autant réduire sa vulnérabilité à la corrosion. La corrosion des cordes de piano est donc un réel problème auquel il faut remédier.
Dans cette partie, on assimilera l'acier au fer.
L'allure du diagramme E-pH du fer à

est donnée en figure B du document réponse. Ce document sera complété et rendu avec la copie.
Ce diagramme est établi pour une concentration de tracé totale en espèces dissoutes de

. La convention de frontière entre deux domaines de prédominance d'espèces dissoutes est l'égalité des concentrations molaires.
Les espèces prises en compte pour ce diagramme sont :

espèces solides : ;
espèces dissoutes : .
III.C.1) Déterminer le degré d'oxydation de l'élément fer dans chaque espèce considérée.

Compléter le diagramme du document réponse en attribuant à chacune des zones l'espèce chimique correspondante. Justifier avec soin votre réponse, en particulier pour le domaine D.
Remarque: la frontière entre les domaines C et D n'est pas tracée.
III.C.2) Déduire du diagramme :

la concentration de tracé ,
le produit de solubilité de ,
la pente de la frontière entre les domaines B et D .
III.C.3) Tracer sur le diagramme la frontière délimitant les domaines C et D . On justifiera avec soin le calcul de sa pente.
III.C.4) Tracer sur ce même diagramme le diagramme potentiel-pH de l'eau pour des pressions gazeuses égales à 1 bar. Les cordes en acier sont-elles attaquées par une eau aérée ? désaérée ? Cela dépend-il du pH ?
III.C.5) Déterminer pour chaque domaine du diagramme s'il s'agit d'un domaine d'immunité, de corrosion ou de passivité. Définir ces trois termes.
III.C.6) Expliquer pourquoi on ne pourrait pas utiliser des cordes en acier avec des raccords de cuivre ? Que se passe-t-il alors ?

IV Polymères synthétiques dans le piano

Si autrefois les touches blanches des pianos étaient recouvertes d'ivoire et les noires d'ébène, aujourd'hui les matériaux de remplacement sont le plastique ou le polymère (ivoire synthétique ou «ivoirine»). De plus, des colles en polymère sont utilisées pour réparer les pianos et coller le bois, comme le polychloroprène (encore appelé Néoprène). Intéressons-nous de plus prêt à cette colle polymère.

IV.A - Étude du monomère : le chloroprène

IV.A.1) Le néoprène est formé à partir de chloroprène, représenté figure 4. Donner son nom dans la nomenclature officielle.

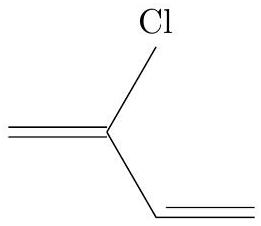
Figure 4 Chloroprène

IV.A.2) La première étape de synthèse du chloroprène consiste en une chloration du buta- 1,3 -diène avec du dichlore. Les réactifs réagissent mole à mole.
a) Écrire l'équation bilan de la réaction en précisant la formule topologique du produit majoritaire obtenu (on ne tient pas compte de la stéréochimie).
b) Indiquer le mécanisme réactionnel en milieu ionique.
c) Le mélange obtenu est-il optiquement actif ? Justifier votre réponse en précisant le (ou les) stéréoisomère(s) obtenu(s) ainsi que leurs proportions relatives. Quelle relation d'isomérie existe-t-il entre eux ?
d) Indiquer pour chaque stéréoisomère la configuration absolue du (ou des) carbone(s) asymétrique(s) en la justifiant.
IV.A.3) Si cette chloration était réalisée sur le (Z)-but-2-ène, combien de stéréoisomères seraient obtenus ? Écrire leur formule topologique et indiquer les relations de stéréoisomérie qui les lient.
En réalité, cette première étape de synthèse du chloroprène est une chloration radicalaire, réalisée à

et sous 1 à 7 bar de dichlore gazeux. Le produit majoritaire est le 1,2 -dichlorobut- 3 -ène qui subit ensuite une déshydrochloration en solution alcaline diluée pour conduire au chloroprène.
IV.A.4) Écrire l'équation bilan de la réaction de déshydrochloration en solution alcaline.

IV.B - Polymérisation du néoprène

En principe il est possible de polymériser le chloroprène par des techniques de catalyse anionique, cationique et de Ziegler-Natta. En raison des propriétés du produit et de considérations économiques, seule la polymérisation radicalaire est employée aujourd'hui.

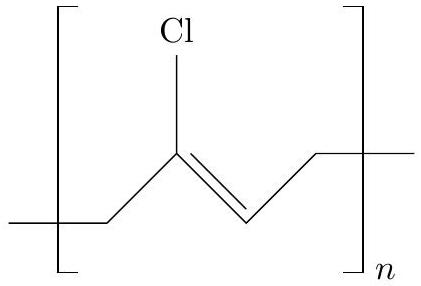
Figure 5 Polychloroprène ou néoprène

IV.B.1) Indiquer la stéréochimie de la double liaison en la justifiant.
IV.B.2) Un échantillon de néoprène a une masse molaire moyenne de

. Quel est son indice de polymérisation moyen?

Données

Pour l'accélération de la pesanteur, on prendra

Constantes fondamentales

Constante des gaz parfaits:

Constante de Faraday :

Constante d'Avogadro:

On prendra:

Grandeurs de référence

Pression standard :

bar

Concentration standard :

Élément	H	C	Cl	Fe	Cu
Numéro atomique	1	6	17	26	29
Masse molaire atomique	1,01	12,0	35,5	55,8	63,5
Rayon atomique	25	70	100	140	135

Grandeurs thermodynamiques à 900 K

	Cu	CuO			CuS
Température de fusion	1356	1599	1508	383	1373		52	198
	0	-75	-103	-438	-47	-101	0	-296
	0	-151	-168	-820	-113	-130	0	-362

Potentiels standard à 298 K par rapport à l'ESH


	0,34	0,00	1,23	0,77				2,00

Prénom :

Signature :

Épreuve de Physique-Chimie Filière PSI

Ne rien porter sur cette feuille avant d'avoir rempli complètement l'en-tête

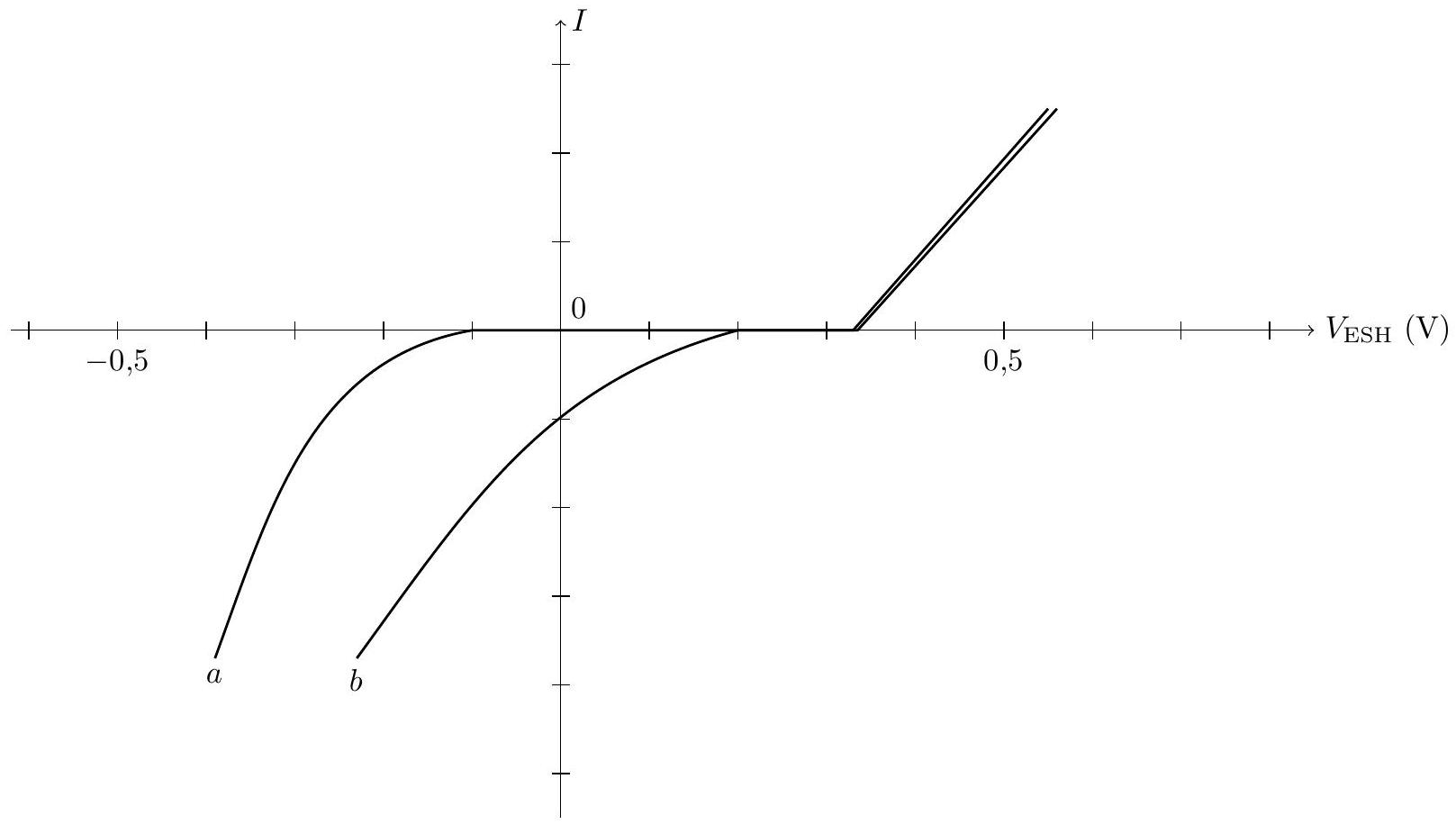
Figure A

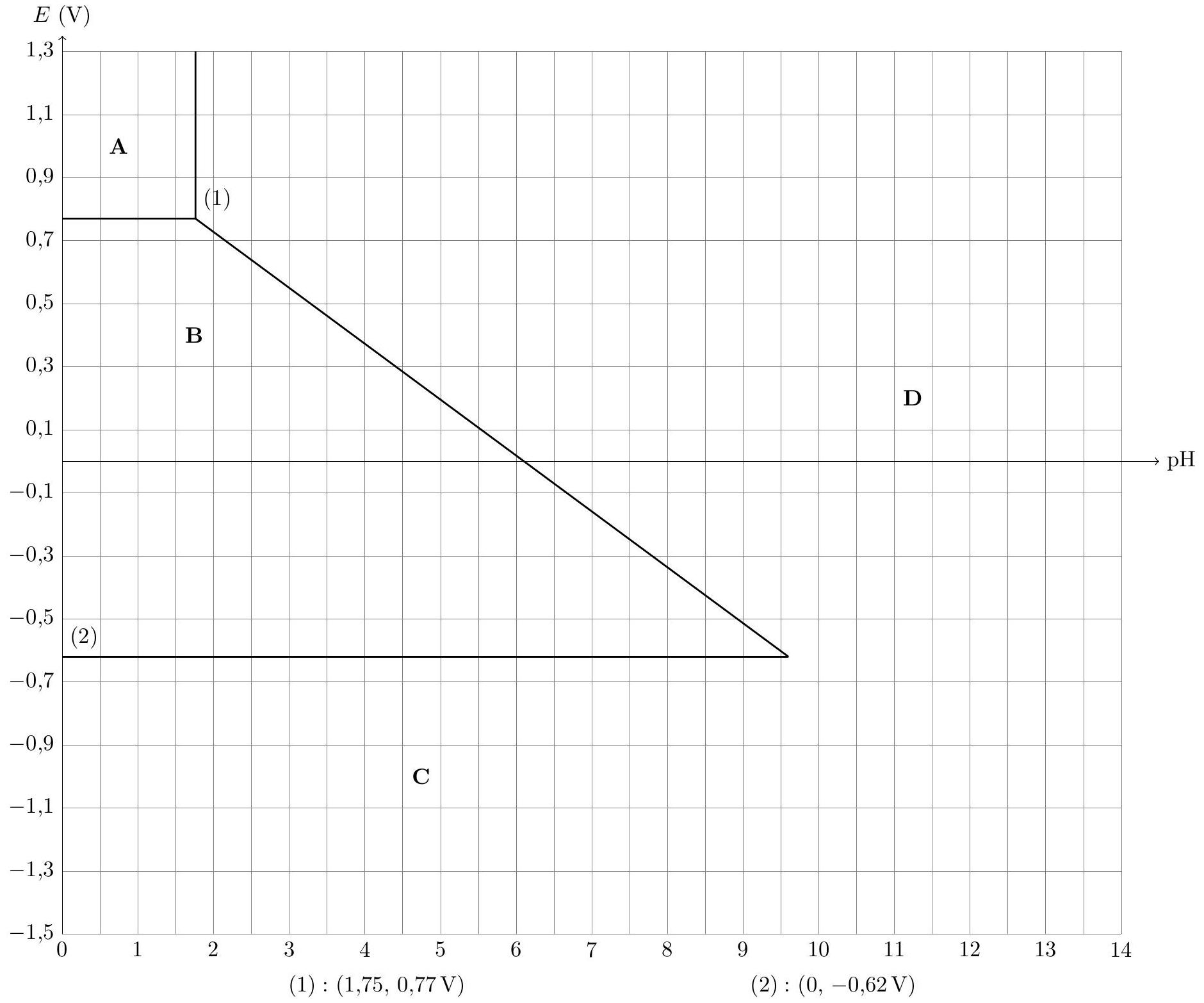
Figure B

Les marteaux sont réalisés en bois recouvert de feutre.
Dans le médium et l'aigu, chaque marteau frappe simultanément deux ou trois cordes identiques pour chaque note.
C'est d'ailleurs la raison pour laquelle on enrobes les cordes de grave avec du cuivre enroulé, plutôt que d'augmenter encore le diamètre du cœur d'acier.