J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

E3A Mathématiques 1 PSI 2015

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Intégrales à paramètresProbabilités finies, discrètes et dénombrementIntégrales généraliséesInformatiquePolynômes et fractions
Logo e3a
🔗 Explorer
Banque
E3A
Année
2015
Filière
PSI
Matière
Maths
E3A PSIE3A 2015PSI MathsMaths 2015
2025_08_29_64ee66d8ed214b1333cfg

e3a 2015 - PSI 1
durée 4 heures - calculatrices interdites

Exercice 1

But de l'exercice

Le jeu d'echec se joue sur un échiquier, c'est à dire sur un plateau de cases. Ces casessont référencées de à (voir figures).
Une pièce, appelée le cavalier, se déplace suivant un "L" imaginaire d'une longueur de deux cases et d'une largeur d'une case.
Exemple (figure 1) : un cavalier situé sur la case atteint, en un seul déplacement, une des huits cases ou .
Dans toute la suite de l'exercice, on appellera case permise toute case que le cavalier peut atteindre en un déplacement à partir de sa position.
Le but de cet exercice est d'écrire un programme faisant parcourir l'ensemble de l'échiquier à un cavalier en ne passant sur chaque case qu'une et une seule fois
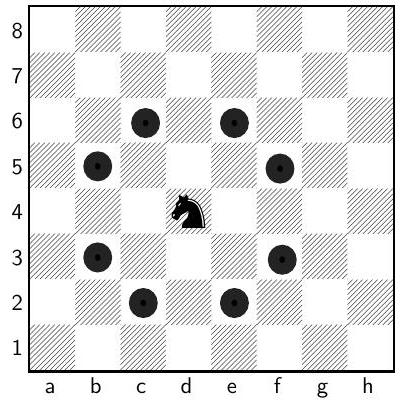
Figure 1
déplacements permis
Figure 2 un exemple
8 56 57 58 59 60 61 62 63
7 48 49 50 51 52 53 54 55
6 40 41 42 43 44 45 46 47
5 32 33 34 35 36 37 38 39
4 24 25 26 27 28 29 30 31
3 16 17 18 19 20 21 22 23
2 8 9 10 y 12 13 14 15
1 0 1 2 3 4 5 6 7
Figure 3 numérotation

Motivation et méthode retenue

Une première idée est de faire parcourir toutes les cases possibles à un cavalier en listant à chaque déplacement les cases parcourues. Lorsque celui-ci ne peut plus avancer, on consulte le nombre de cases parcourues.
  • Si ce nombre est égal à , alors le problème est résolu.
  • Sinon, il faut revenir en arrière et tester d'autres chemins.
  1. Exemple : on considère le parcours suivant d'un cavalier démarrant en (figure 2)
Avec ce début de parcours, au déplacement suivant :
(a) le cavalier va en . Peut-il accomplir sa mission?
(b) le cavalier ne va pas en . Peut-il accomplir sa mission?
Il convient donc dans la résolution du problème proposé d'éviter de se retrouver dans la situation repérée en cette première question.
Dans tout ce qui suit, nous nommerons coordonnées d'une case la liste d'entiers où représente le numéro de ligne et le numéro de colonne (tous deux compris entre 0 et 7 ). Par exemple, la case b3 a pour coordonnées .
D'autre part, les cases sont numérotées de 0 à 63 en partant du coin gauche comme indiqué en figure 3.
Nous appellerons indice d'une case, l'entier ainsi déterminé. a, par exemple, un indice égal à 17 .
2. Ecrire une fonction indice qui prend en argument la liste des coordonnées d'une case est renvoie son indice. Ainsi, indice ( ) doit être égal à 17 .
3. Ecrire une fonction coord qui à l'indice d'une case associela liste de ses coordonnées. Ainsi coord (17) doit être égal à .
4. On considère la fonction Python CasA suivante :
def CasA(n):
    Deplacements= [[1,-2], [2,-1], [2,1], [1,2], [-1,2], [-2,1], [-2,-1], [-1,-2]]
    L= []
    i,j=Coord(n)
    for d in Deplacements:
        u=i+d[0]
        v=j+d[1]
        if }\textrm{u}>=0\mathrm{ and }\textrm{u}<8\mathrm{ and }\textrm{v}>=0\mathrm{ and }\textrm{v}<8\mathrm{ :
            L.append(Indice([u,v]))
    return(L)
(a) Que renvoient CasA(0) et CasA(39).
(b) Expliquer en une phrase ce que fait cette fonction.
5. Ecrire une fonction Init ne prenant aucun argument et qui modifie deux variables globales ListeCA et ListeCoups. ListeCoups recevra la iste vide. ListeCA recebra une listede 64 éléments. Chaque élément listeCA (pour ) devra contenir la liste des indices des cases qu'un cavalier peut atteindre en un coup à partir de la cas d'indice .
6. Après exécution de la fonction Init(), la commande ListeCA[n] renvoie-t-elle [5], [10,17], ou une autre valeur?
7. Au cours de la recherche, lorsqu'on déplace le cavalier vers la case d'indice , cet indice doit être retiré de la liste des cases permises à partir de la position .
Exemple : après exécution de la fonction Init(), la liste des cases permises depuis est et ListeCA [1] = [16, 18, 11]. La liste des cases permises depuis est [ ] et ListeCA [16] .
Puis, on choisit de commencer le parcours en posant le cavalier en . Cette case doit donc être retirée de la liste des cases permises de et . En particulier pour , la liste ListeCA [16] devient [33,26,10].
Cette méthode nous permet de détecter les blocages : le cavalier arrive sur la case d'indice , est alors retiré de toutes les listes ListeCA [k] pour toute case permise pour . Si dès lors l'une de ces listes devient vide, nous dirons que nous somme alors dans une situation critique, cela signifiera que la case d'indice ne peut plus être atteinte que depuis la case d'indice . Par conséquent,
  • si le cavalier se déplace sur une autre case que celle d'indice , alors cette dernière ne pourra plus jamais être atteinte;
  • si le cavalier se déplace sur la case d'indice , il est bloqué pour le coup suivant. Soit la mission est accomplie, soit le cavalier n'a pas parcouru toutes les cases.
Le programme va réaliser la recherche en maintenant à jour la variable globale ListeCoups afin qu'elle contienne en permanence la liste des positions successives occupées par lecavalier au cours de ses tentatives de déplacement. Nous avons alors besoin d'écrire trois fonctions.
(a) Ecrire une fonction OccupePosition qui
  • prend comme argument un entier (indice d'une case), l'ajoute à la fin de la variable globale ListeCoups,
  • puis enlève de toutes les listes ListeCA[k] pour toutes les cases permises depuis la case d'indice ,
  • renvoie enfin la valeur True si nous sommes dans une situation critique et False sinon.
On pourra utiliser la méthode remove qui permet de retirer d'une liste le premier élément égal à l'argument fouri. Si l'argument ne fait pas partie de la liste, une erreur sera retournée

L.remove(2) # modifie en [ ]
L.remove(6) # provoque une erreur
(b) Ecrire une fonction LiberePosition qui ne prend pas d'argument et qui
  • récupère le dernier élément de la variable globale ListeCoups (i.e. l'indice de la dernière case jouée à l'aide de la fonction OccupePosition),
  • puis l'enlève de ListeCoups,
  • et enfin, qui ajoute à toutes les listes ListeCA [k] pour toutes les cases d'indice permises depuis la case d'indice .
    On pourra utiliser la méthode pop qui renvoie le dernier élément d'une liste et le supprime de cette même liste.

    et
    (c) Ecrire une fonction TestePosition d'argument un entier (indice d'une case) qui :
  • occupe la position d'indice ,
  • vérifie si la situation est critique.
Si c'est le cas, la fonction vérifiera si les 63 cases sont occupées et, dans ce cas renverra True pour indiquer que la récecherche est terminée. Si les 63 cases ne sont pas occupées, la fonction libérera la case d'indice et renverra False.
Dans le cas contraire, la fonction vérifiera avec TestePosition toutes les cases d'indice jouables après celle d'indice (on prendra garde à affecter une variable locale avec la liste ListeCA [n] puisque celle-ci risque d'être modifiée lors des appels suivants). La fonction retournera True dès que l'un des appels à TestePosition retourne True ou libérera la case d'indice et retournera False sinon.
8. Afin de réduire notablement la complexité temporelle du programme, on part du proncipe qu'il faut tester en priorité les cases ayantv le moins de cases permises possibles. On appellera valuation d'une case d'indice le nombre de cases permises pour cette case.
(a) Ecrire une fonction valuation qui prend comme argument un indice de case en entrée et renvoie la valuation de cette case.
(b) Ecrire une fonction Fusion qui prend comme arguments deux listes et d'entiers entre 0 et 63 ; on suppose ces listes triées par ordre croissant de valuation de leurs éléments; l'appel fusion (A,B) retourne comme valeur la liste fusionnée de tous les éléments de A et B triée par ordre croissant de valuation de ses éléments.
(c) Ecrire une fonction TriFusion qui prend en argument une liste L d'entiers compris entre 0 et 63 et qui retourne comme valeur la liste de tous les éléments de L triée par valuation croissante de ses éléments.
(d) Modifier la fonction TestePosition pour qu'elle agisse ainsi que l'on a décidé en début de question.

Exercice 2

  1. Soit . Déterminer une condition nécessaire et suffisante pour que soit diagonalisable dans .
  2. On note et son complémentaire dans . Prouver que est un ensemble dénombrable.
  3. Soient ( ) un espace probabilisable et définie de dans par
Déterminer pour qu'il existe une probabilité tel que soit la loi de probabilité d'une variable aléatoire définie sur et à valeurs dans . Préciser .
4. Déterminer et la loi de probabilité de .
5. Déterminer l'espérance de la variable aléatoire .
6. Déterminer la fonction génératrice de la variable aléatoire . Retrouver alors la valeur de obtenue à la question précédente.
7. Soit une variable aléatoire définie sur , indépendante de la variable aléatoire et suivant la loi
Soit alors la variable aléatoire définie sur par . Déterminer la fonction génératrice de . En déduire sa loi de probabilité.
8. Déterminer enfin la probabilité pour que la matrice soit diagonalisable.

Exercice 3

On pose, lorsque cela est possible
  1. Déterminer l'ensemble de définition de .
  2. En justifiant son existence, calculer .
  3. Calculer . On pourra utiliser l'application .
  4. Calculer . On pourra remarquer que la dérivée de est égale .
  5. Vérifier que est positive sur .
  6. Montrer que est décroissante sur .
  7. Prouver que est de classe sur et préciser l'expression de . Retrouver alors le résultat de la question précédente.
  8. Soit . Démontrer la relation
On pourra effectuer, en la justifiant, une intégration par parties.
9. Soit . Donner l'expression de à l'aide de factorielles.
10. Pour tout réel , on pose
Prouver que . Calculer pour tout .
11. En utilisant la question précédente, déterminer un équivalent de quand .
12. Vérifier que . En déduire que
  1. En utilisant des parties entières, prouver que
  1. Déduire des questions précédentes le tableau des variations de sur et tracer sa courbe représentative dans un repère orthonormé.
  2. Prouver que la fonction est constante sur .

Exercice 4

Dans tout l'exercice, pour tout entier naturel , on identifie polynôme de et fonction polynomiale associée pour la structure d'espace vectoriel normé.
  1. Soit un élément de unitaire (le terme de plus haut degré de est égal à 1).
    (a) Soit . Montrer que .
    (b) On suppose dans cette question que est scindé sur . En utilisant une factorisation de , montrer que
où désigne le degré du polynôme .
(c) On prend dans cette question .
(a) Donner une factorisation de dans .
(b) Trouver tel que .
(d) On suppose dans cette question que . Montrer que toutes les racines de sont réelles. En déduire que est scindé sur .
(e) Enoncer clairement le résultat obtenu.
2. Soient un entier naturel non nul et une suite de matrices trigonalisables de qui converge vers une matrice . On appelle pour tout entier naturel le polynôme caractéristique de et celui de la matrice .
(a) Donner le degré et le coefficient dominant de .
(b) Prouver que .
(c) En déduire que est trigonalisable.
(d) Qu'en conclut-on pour l'ensemble des matrices trigonalisables de ?
3. On prend dans cette question et où est un entier non nul.
(a) Déterminer .
(b) Etudier la diagonalisabilité des matrices et dans .
(c) Conclure.
E3A Mathématiques 1 PSI 2015 - Version Web LaTeX | WikiPrépa | WikiPrépa