Version interactive avec LaTeX compilé
CONCOURS ENSAM - ESTP - ARCHIMEDE
Épreuve de Physique PC
Durée 4 h
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
L'usage de calculatrices est autorisé.
Ce problème étudie l'humidité de l'atmosphère. L'épreuve est divisée en deux parties totalement indépendantes. Divers aspects thermodynamiques d'un air humide sont abordés en première partie. Deux hygromètres, appareils destinés à mesurer l'humidité de l'air, sont étudiés en seconde partie : le psychromètre (appareil développé par Regnault au
Remarques préliminaires importantes: il est rappelé aux candidat(e)s que :
- les explications des phénomènes étudiés interviennent dans la notation au même titre que les développements analytiques et les applications numériques;
- tout au long de l'énoncé, les paragraphes en italiques ont pour objet d'aider à la compréhension du problème mais ne donnent pas lieu à des questions;
- tout résultat fourni dans l'énoncé peut être admis et utilisé par la suite, même s'il n'a pas été démontré par les candidat(e)s ;
- les applications numériques seront données avec le nombre de chiffres significatifs adapté en fonction des données de l'énoncé. A défaut, elles seront comptées fausses.
Dans tout le problème, et sauf mention explicite du contraire :
- la pression sous laquelle sont étudiés les phénomènes est la pression atmosphérique, dont la valeur numérique est
bar; - le symbole
désigne la température en degré Celsius , tandis que représente la température en Kelvin (K) ; - la constante des gaz parfaits est
.
Il est nécessaire de savoir mesurer et contrôler l'humidité de l'air dans un certain nombre de processus industriels où la teneur en eau d'une phase gazeuse doit être strictement encadrée, mais aussi dans des appareils à usage domestique comme les climatiseurs, les humidificateurs ou encore les contrôleurs d'humidité utilisés dans l'industrie du bâtiment.
PREMIỂRE PARTIE ETUDE THERMODYNAMIQUE DE L'AIR HUMIDE
A / RELATIONS GÉNÉRALES
Considérons un volume
Etudions les caractéristiques thermodynamiques de ce mélange gazeux.
A1. Justifier que
Montrer que
L'humidité absolue est définie par le rapport
A2. Montrer que le rapport
Donner l'expression de la constante
En déduire
Application numérique : calculer
Un air humide à la température
A1. Justifier que
Montrer que
L'humidité absolue est définie par le rapport
A2. Montrer que le rapport
Donner l'expression de la constante
En déduire
Application numérique : calculer
Un air humide à la température
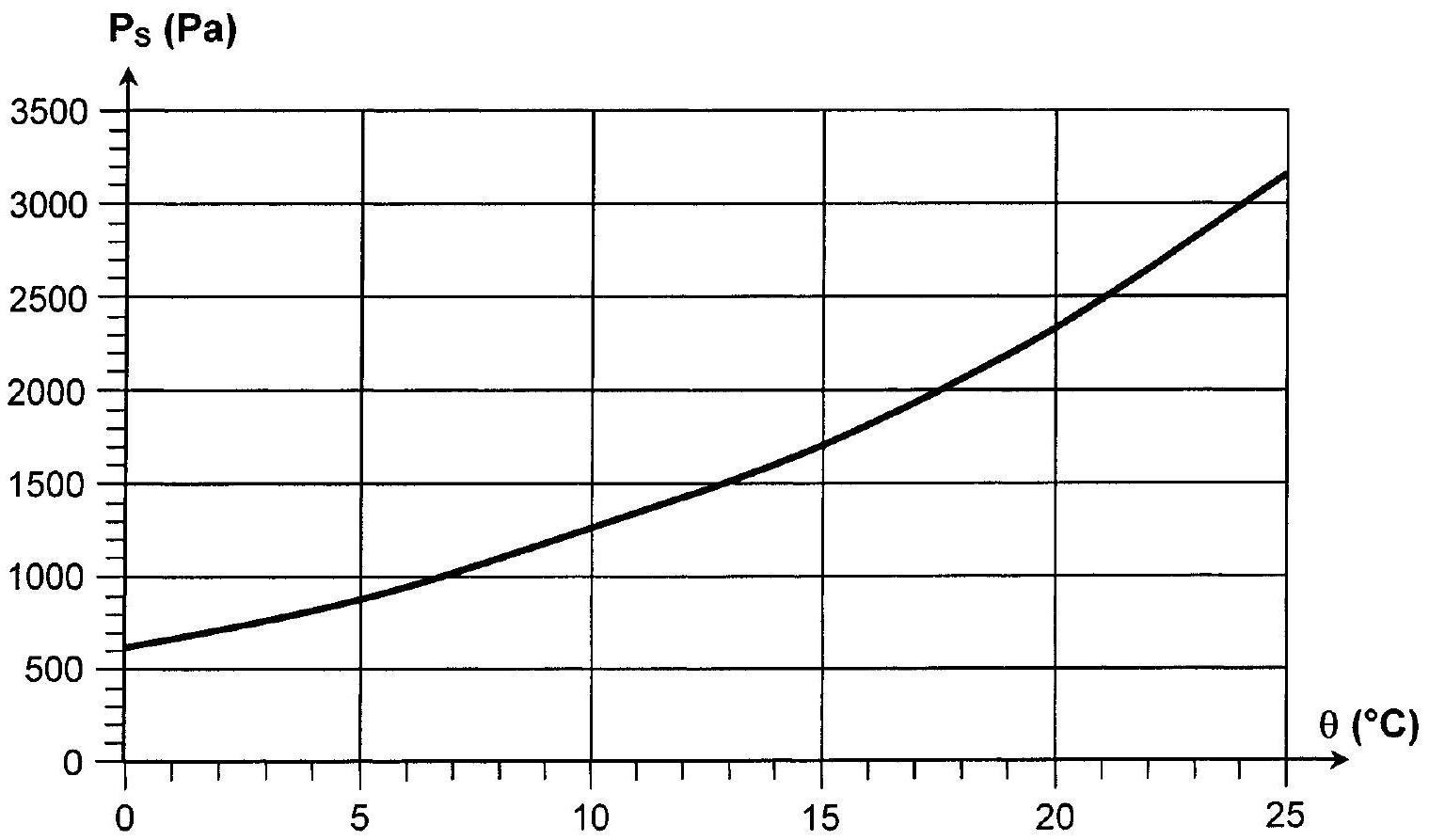
Figure 1 : Pression de vapeur saturante en fonction de la température
L'humidité relative est définie par
A3*a. Quelle est la caractéristique d'un air tel que
A3*a. Quelle est la caractéristique d'un air tel que
A3b. La température et la pression étant fixées, déterminer la valeur maximale
Application numérique : calculer
A3c. Comment évolue
Application numérique : calculer
A3c. Comment évolue
A4*a. L'intérieur d'un local de volume
A4*b. Durant la nuit, le local n'est pas chauffé et sa température descend à
Considérons à la température
A5a. Quelle est la température de rosée
A5*b. Une lame métallique en contact avec de l'air humide est refroidie progressivement sous la pression constante
A5*b. Une lame métallique en contact avec de l'air humide est refroidie progressivement sous la pression constante
B / ÉTUDE DE L'ÉQUILIBRE THERMODYNAMIQUE EN VASE CLOS (UTILISATION DES POTENTIELS THERMODYNAMIQUES)
Considérons un système fermé (&) formé de
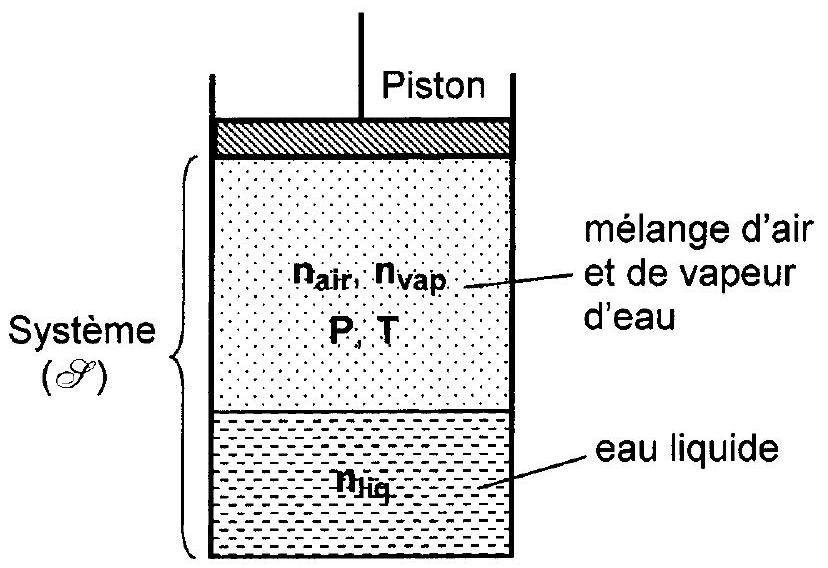
Figure 2
B1. Rappeler la définition d'un potentiel thermodynamique.
Le système (
Soient
B2. Montrer que
Supposons que (
Supposons que (
B3*a. Montrer que dans cette transformation particulière
où
Rappelons que, d'après le cours de chimie, l'expression générale du potentiel chimique d'un constituant
Rappelons que, d'après le cours de chimie, l'expression générale du potentiel chimique d'un constituant
où
D'autre part, la pression de vapeur saturante de l'eau
B3*b. En déduire l'expression de
Considérons un état initial dans lequel les nombres de moles de liquide et de vapeur d'eau sont respectivement
B3*c. Comment le système évolue-t-il si
B3*d. La température du thermostat est
i)
ii)
i)
ii)
C / ÉVAPORATION DE L'EAU LIQUIDE
Etudions maintenant quelques caractéristiques physiques de l'évaporation de l'eau liquide dans l'atmosphère. Contrairement à l'ébullition qui est un phénomène nécessitant un apport d'énergie sous forme de chaleur et qui se produit à une température bien définie (température de vaporisation) pour une pression donnée, l'évaporation de l'eau liquide dans l'atmosphère est un phénomène très lent qui se produit à toute température. Ce phénomène résulte d'un couplage entre la diffusion particulaire des molécules d'eau dans l'air et des transferts thermiques entre le liquide et l'atmosphère.
Considérons un modèle unidimensionnel dans lequel une couche d'eau liquide possède une surface libre plane en contact avec l'atmosphère. Du fait de l'évaporation, la hauteur h(t) de cette surface libre décroît au cours du temps. Le liquide repose sur un fond (situé en

Figure 3
Les hypothèses du modèle sont les suivantes:
- la pression est uniforme et constante ;
- l'air constitue un milieu immobile à la température constante
, au sein duquel diffusent les molécules d'eau avec une densité particulaire ; le vecteur densité de courant particulaire est noté et le coefficient de diffusion ; - la phase liquide est immobile et la densité particulaire de molécules d'eau nliq est supposée stationnaire et uniforme.
C1* Rappeler la loi de Fick et en donner le sens physique.
En raisonnant sur un cylindre de hauteur élémentaire dz et de surface de base
En raisonnant sur un cylindre de hauteur élémentaire dz et de surface de base
Considérons un instant to donné et définissons le cylindre (%) dont la première base repose sur le fond et dont l'autre base est située au niveau de la surface libre du liquide à cet instant. Ce cylindre possède une hauteur H constante qui est égale à la hauteur h(to) de liquide à l'instant considéré, ainsi que deux bases de même surface S. (figure 3)
C2*a. Déterminer la variation dN du nombre de molécules d'eau contenues dans (%) entre les instants
C2*b. Compléter ce bilan en reliant dN à la densité de courant j des molécules de vapeur d'eau sur la base supérieure du cylindre (
(l'instant
L'évaporation de l'eau liquide entraîne des transferts thermiques à la fois au sein du liquide et à l'interface liquide-atmosphère. Pour modéliser ces échanges, supposons que l'eau liquide est caractérisée par une conductivité thermique
L'évaporation de l'eau liquide entraîne des transferts thermiques à la fois au sein du liquide et à l'interface liquide-atmosphère. Pour modéliser ces échanges, supposons que l'eau liquide est caractérisée par une conductivité thermique
C3. Rappeler l'expression de la loi de Fourier et établir l'équation de diffusion thermique à laquelle obéit la température au sein du liquide.
Précisons en outre que les échanges thermiques entre le liquide et l'air sont régis par la loi de Newton : la puissance thermique qui traverse une surface élémentaire dS située à la surface libre du liquide est donnée par:
C4. Considérons une tranche élémentaire de liquide d'épaisseur dz et de surface
où
Par la suite, notons
Par la suite, notons
C5*a. Montrer que
C5*b. Déduire de l'étude précédente que le coefficient
C5*c. Quel est le signe de a ? La température moyenne du liquide est-elle diminuée ou augmentée par le phénomène d'évaporation? Cette modification a-t-elle tendance à renforcer ou à limiter le phénomène ?
La variation de température induite par évaporation peut être utilisée pour mesurer l'humidité de l'air, comme nous le verrons dans la partie suivante.
DEUXIEME PARTIE MESURE DE L'HUMIDITE DE L'AIR HUMIDE
A / PSYCHROMÈTRE
Un psychromètre est un appareil destiné à mesurer l'humidité de l'air par la mesure d'une différence de température.
La pointe d'un thermomètre, entourée d'un coton imbibé d'eau liquide, est placée dans un courant d'air humide, ce qui a pour effet de provoquer l'évaporation du liquide et l'enrichissement de la phase gazeuse en vapeur d'eau (figure 4).
La température de l'eau liquide (indiquée par le thermomètre) est constante et vaut
La température de l'eau liquide (indiquée par le thermomètre) est constante et vaut
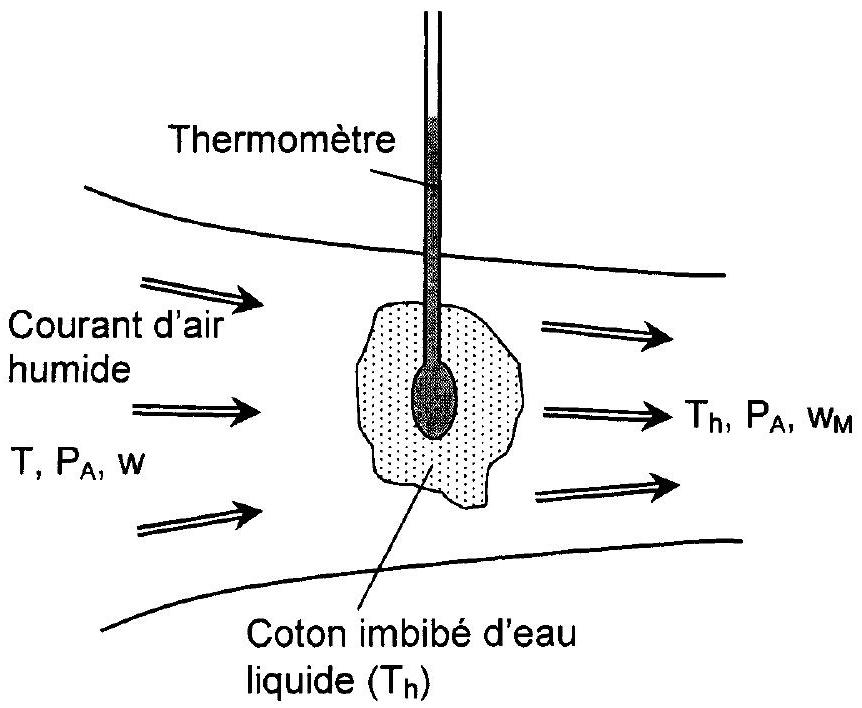
Figure 4
température est alors
La transformation s'effectue sous la pression atmosphérique constante
Définissons le système (%) constitué d'une masse mair d'air sec mélangé à une masse
(
Définissons le système (%) constitué d'une masse mair d'air sec mélangé à une masse
(
A1. Expliciter la relation existant entre
La transformation est suffisamment rapide pour que les échanges de chaleur entre (
La transformation est suffisamment rapide pour que les échanges de chaleur entre (
A2. Montrer que l'enthalpie H de (
L'air humide étant un mélange idéal de gaz parfaits, son enthalpie est la somme des enthalpies de chaque constituant du mélange ;
L'air humide étant un mélange idéal de gaz parfaits, son enthalpie est la somme des enthalpies de chaque constituant du mélange ;
D'autre part, l'étude de la première partie a permis d'établir que
A3. Montrer l'égalité suivante:
A4*a. En déduire que l'humidité absolue
A4*a. En déduire que l'humidité absolue
A4*b. En réalité, la variation de température n'excède pas quelques degrés. Compte tenu des ordres de grandeur des différents termes et à l'aide des données numériques ci-dessous, simplifier l'équation précédente et montrer qu'elle peut s'écrire sous la forme :
Donner l'expression de la constante
Données numériques :
Cette méthode est utilisée pour mesurer l'humidité relative
Le psychromètre est constitué de deux thermomètres soumis au même courant d'air. Le premier est au contact direct de l'air et mesure
A5. Une mesure particulière a donné pour l'air d'un local :
En pratique, l'humidité relative
B / HYGROMÈTRE CAPACITIF
Certains oxydes métalliques comme
où
Ce type de condensateur est réalisé à partir d'une lame d'aluminium constituant l'une des armatures, sur laquelle est déposée une couche d'alumine poreuse. La seconde armature du condensateur est une lame d'or. La mesure de la capacité de ce type de condensateur constitue actuellement une technique fiable et précise pour déterminer l'humidité relative.
Ce type de condensateur est réalisé à partir d'une lame d'aluminium constituant l'une des armatures, sur laquelle est déposée une couche d'alumine poreuse. La seconde armature du condensateur est une lame d'or. La mesure de la capacité de ce type de condensateur constitue actuellement une technique fiable et précise pour déterminer l'humidité relative.
Etudions dans cette partie un montage électrocinétique permettant la mesure de
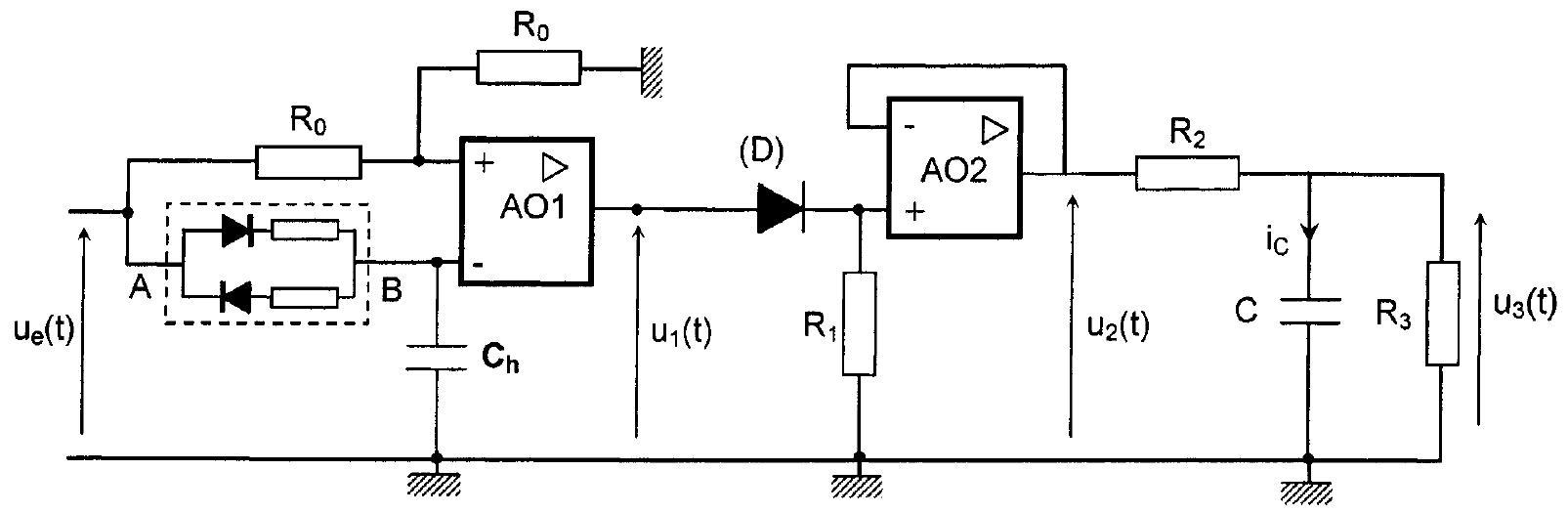
Figure 5 : Schéma électrique complet de l'hygromètre
Les diodes utilisées (fiqure 6) sont supposées idéales, ce qui signifie :

Figure 6
B1. Quelle est l'origine physique de la variation de la constante diélectrique de l'alumine
B2. La capacité étudiée varie de 110 pF à 250 pF lorsque l'humidité relative
Considérons le dipôle (AB) représenté sur la figure 7, pour lequel (
B3. Montrer que les deux diodes ne peuvent pas être simultanément dans le même état. Déterminer, selon le signe de la tension u, le résistor ohmique équivalent à (AB).
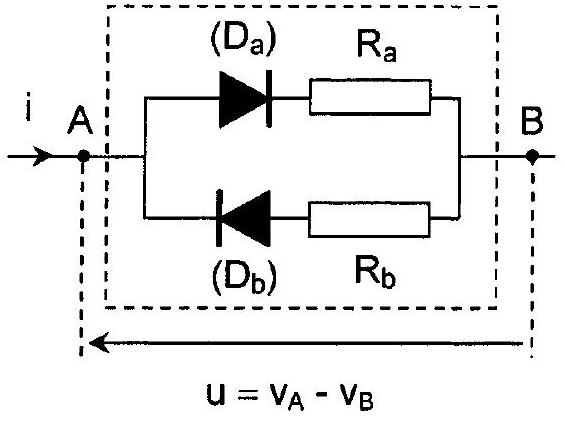
Figure 7
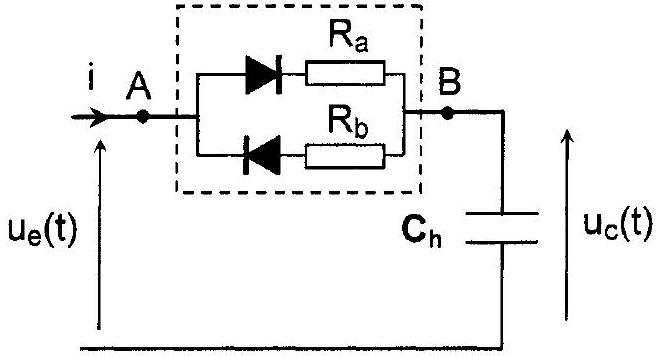
Figure 8
Ce dipôle est maintenant inséré dans le montage de la figure 8 dans lequel
B4*a. Établir l'équation différentielle vérifiée par
À partir de l'instant
B4*b. Quelle est alors l'équation différentielle vérifiée par
B4*b. Quelle est alors l'équation différentielle vérifiée par
B4*c. Représenter l'allure de
Dans le montage de la figure 9a, l'amplificateur opérationnel (AO1) est supposé idéal et fonctionne en régime de saturation. Les tensions de saturation haute et basse sont notées respectivement
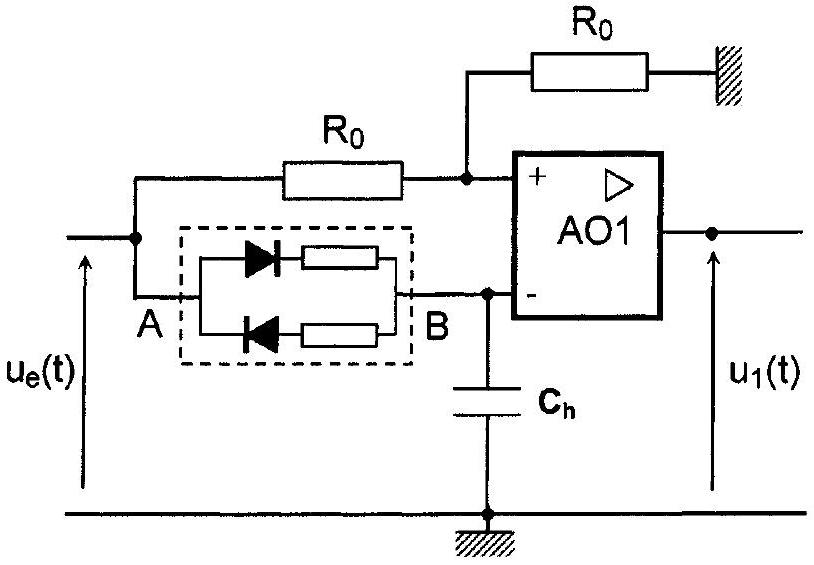
Figure 9a

Figure 9b
Le régime permanent est supposé établi : toutes les tensions sont périodiques avec la même période
B5*a. Expliciter la condition reliant
Déterminer, en fonction de
Déterminer, en fonction de
B5*b. Évaluer la valeur minimale de
B5*c. En choisissant les valeurs numériques suivantes :
Le montage représenté sur la figure 10 est destiné à mettre en forme la tension
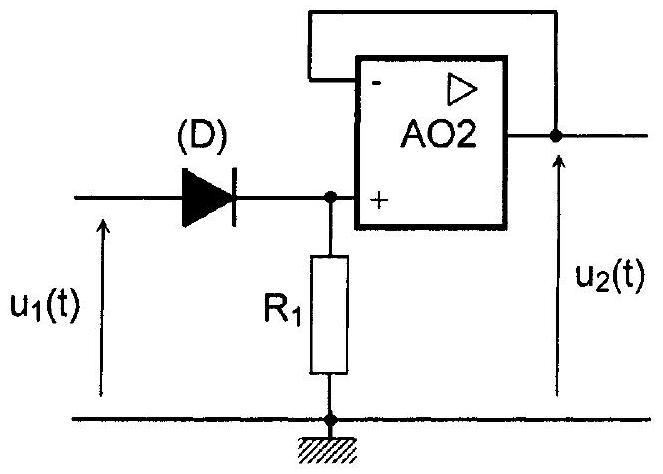
Figure 10
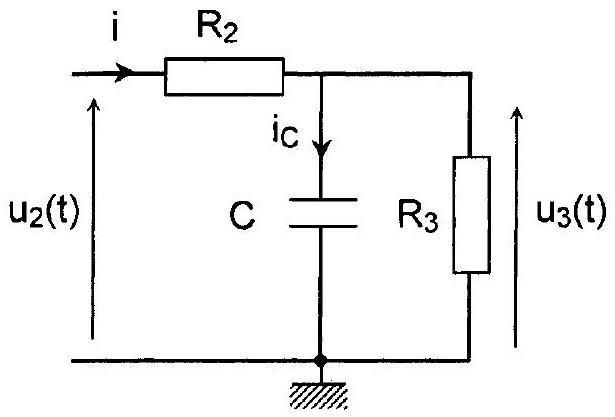
Figure 11
B6. Déterminer, selon le signe de
Cette tension u2 est appliquée à l'entrée du filtre passif représenté sur la figure 11 et constitué de deux résistances
Le régime permanent étant établi, la tension
Etant donnée une fonction
B7a. Calculer la valeur moyenne de
B7b. Montrer que la valeur moyenne
B7b. Montrer que la valeur moyenne
Afin d'alléger les expressions littérales intervenant dans les questions suivantes, posons la quantité
B8*a. Écrire l'équation différentielle du premier ordre à laquelle obéit
B8*b. Quelle est l'équation différentielle satisfaite par
B8*c. Montrer que
Le taux d'ondulation
B8*d. Déterminer l'expression du taux
Application numérique: calculer
B8*d. Déterminer l'expression du taux
Application numérique: calculer
B8*e. Sur quels facteurs est-il possible de jouer pour diminuer le taux d'ondulation
Au contact de l'air ambiant d'un local, le dispositif délivre une tension
B9. Déterminer l'humidité relative
Au contact de l'air ambiant d'un local, le dispositif délivre une tension
B9. Déterminer l'humidité relative
