J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Physique Chimie L PC 2018

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2018
Filière
PC
Matière
Physique Chimie
X-ENS PCX-ENS 2018PC Physique ChimiePhysique Chimie 2018
2025_09_04_4814b62d471c692cbe09g

ÉCOLE NORMALE SUPÉRIEURE DE LYON

CONCOURS D'ADMISSION 2018

FILIÈRE PC

COMPOSITION DE PHYSIQUE-CHIMIE - (L)

(Durée : 5 heures)
L'usage de calculatrice n'est pas autorisé pour cette épreuve. Les résultats des applications numériques seront donnés avec un chiffre significatif.
Les candidats devront impérativement rédiger les parties relatives à la chimie et à la physique sur des copies distinctes et sur lesquelles ils porteront, de façon claire, les mentions correspondantes, "Сhimie" ou "РhySIQUE".
Les candidats indiqueront très clairement les références des questions abordées.
Cette épreuve comprend deux parties indépendantes. La première, consacrée à la physique, s'intéresse à l'appparition de l'instabilité de ROSENSWEIG à l'interface d'un ferrofluide. La seconde, dédiée à la chimie, étudie l'obtention et la caractérisation des nitrures de fer par différents procédés. Chacune de ces parties participe à part égale au barème global.

Partie Physique
Étude de l'instabilité de Rosensweig

1 Cadre de l'étude.

Un ferrofluide est un fluide contenant des nanoparticules magnétiques en suspension. Ces particules possédant une perméabilité magnétique relative ( ) élevée, le fluide peut acquérir une forte aimantation sous l'action d'un champ magnétique. Une conséquence remarquable de cette propriété est l'apparition d'une déformation de son interface avec l'air lorsqu'il est soumis à un champ magnétique vertical et uniforme, lorsque l'intensité de ce champ devient suffisante. La figure (1) illustre ce phénomène connu sous le nom d'instabilité de Rosensweig. Nous nous proposons d'étudier ce phénomène en vue de déterminer sous quelle condition une interface, intialement plane, se déstabilise pour faire apparaître une structure régulière. Les cinq sections de cette étude ne sont pas indépendantes.
Figure 1 - Instabilité de Rosensweig dans un champ magnétique vertical uniforme (en géométrie circulaire). L'interface fluide-air présente un motif régulier formé d'un ensemble de "pointes".
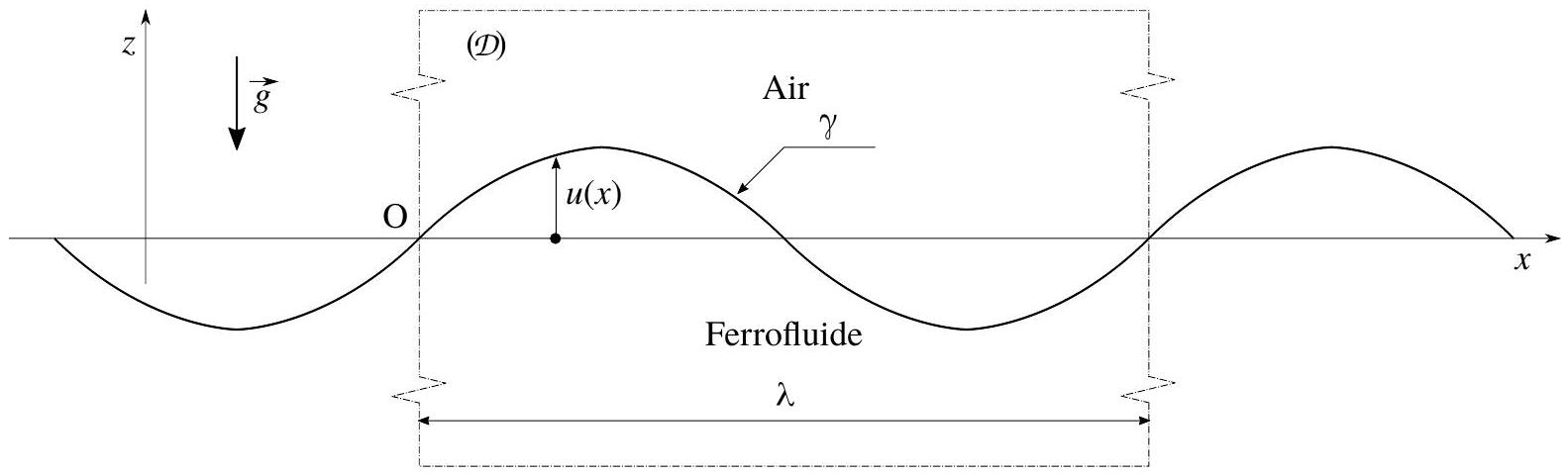
Nous décrivons la déformation de l'interface par le déplacement de chacun de ses points par rapport à sa configuration plane. Ce champ de déplacement est supposé vertical, invariant selon la direction ( ) et tel que . Dans cette approximation des faibles déformations, nous l'écrivons sous la forme :
ù
Figure 2 - Déformation sinusoïdale de l'interface ferrofluide-air dans l'approximation des faibles déformations . Son état géométrique de référence est le plan . La zone délimitée par la frontière en trait pointillé définit le domaine d'étude .
L'état de référence de l'interface est défini par le plan ( ). Nous lui associons l'énergie potentielle nulle. La figure (2)

2 Énergie de surface.

Il s'agit d'exprimer l'énergie potentielle de surface associée à la tension superficielle et la déformation de l'interface comprise dans le domaine . Nous rappelons que l'élément de longueur d d'une courbe plane définie par une fonction s'exprime:
  1. Exprimer sous forme d'une intégrale. Comme cela est indiqué dans la présentation de l'étude (section (1)), nous rappelons que la référence des énergies potentielles correspond à une interface plane ( ).
  2. En déduire l'expression de dans la limite des faibles déformations. On exprimera cette énergie en fonction de , résume le cadre de cette étude.
    Le domaine de ferrofluide sur lequel porteront les bilans d'énergie est le parallélépipède dont la frontière, dans le plan ( ), est représentée par un rectangle en trait pointillé. Nous notons la masse volumique du ferrofluide (celle de l'air sera négligée devant ), le champ de pesanteur et l'énergie de surface (ou tension superficielle) de l'interface ferrofluide-air. Nous supposons cette interface d'extension infinie.
  3. Traduire, sur les paramètres et de la fonction , l'approximation des faibles déformations.
  4. Justifier que le champ de déplacement sinusoïdal adopté (relation (1)) ne restreint pas la généralité de l'étude dans la limite des faibles déformations.
  5. En reproduisant la figure (2), indiquer par des flèches les flux de ferrofluide qui accompagnent la déformation de l'interface depuis son état de référence. Justifer alors que le domaine peut être considéré comme fermé vis-à-vis des bilans énergétiques. et . Récrire cette grandeur en remplaçant le préfacteur numérique qui apparaît dans son expression par 1. C'est toujours sous cette forme que cette énergie sera écrite par la suite.
    N.B. : Dorénavant, et jusqu'à la fin de cette étude, cette approximation sera régulièrement utilisée. Pour mentionner qu'un résultat est donné dans ce cadre, on remplacera alors le signe " " par le signe " ".

3 Énergie de pesanteur.

Exprimons l'énergie potentielle de pesanteur associée à la gravité et à la déformation .
6. En s'appyant sur la réponse à la question (3), indiquer, à l'aide d'un schéma, le transfert de masse qu'il faut effectuer, à l'intérieur du domaine , pour former l'interface déformée sinusoïdalement à partir d'une interface plane. En raisonnant qualitativement, c'est-à-dire sans calcul (d'intégrale, notamment), exprimer la dépendance de avec les grandeurs et . Ici encore, on remplacera tout préfacteur numérique par 1.
7. Préciser, sur le même schéma, l'élévation de la masse correspondant à ce transfert. Dans l'esprit de la question précédente, l'exprimer en fonction de la grandeur caractéristique appropriée (toujours sans calcul et sans préfacteur numérique).
8. En déduire la dépendance de avec et (sans préfacteur numérique).

4 Analyse de stabilité de l'interface sans champ magnétique.

Déterminons si une interface, intialement plane, est susceptible d'évoluer spontanément vers un état d'ondulation. Étudions ensuite son comportement dynamique.
Se reporter au N.B. en fin de question (5).
9. Vérifier que l'énergie potentielle totale du domaine s'écrit :
  1. Former, par considération dimensionnelle, une longeur caractéristique à partir des grandeurs et .
  2. Nous posons . Exprimer sous la forme :
où est une énergie caractéristique (positive) que l'on exprimera et une fonction que l'on explicitera.
12. Représenter graphiquement la dépendance de la fonction avec .
13. Analyser la stabilité de l'interface à partir de ce tracé.
  • Nous souhaitons maintenant étudier le comportement dynamique de l'interface afin de décrire son évolution temporelle. Nous considérons alors que l'amplitude est une fonction du temps que nous recherchons, toujours sous l'hypothèse des faibles déformations, sous la forme :
ù
Dans le but d'exprimer l'énergie cinétique du ferrofluide nous simplifions la géométrie de l'écoulement pour ne retenir que ses caractéristiques essentielles. Nous considérons que sa vitesse est globalement verticale sous les bosses et les creux en formation, et globalement horizontale entre creux et bosse (flux assurant le transfert de fluide). La perturbation de l'interface ayant une portée verticale de l'ordre de la longueur d'onde, la hauteur du "canal" d'écoulement horizontal est choisie égale à . 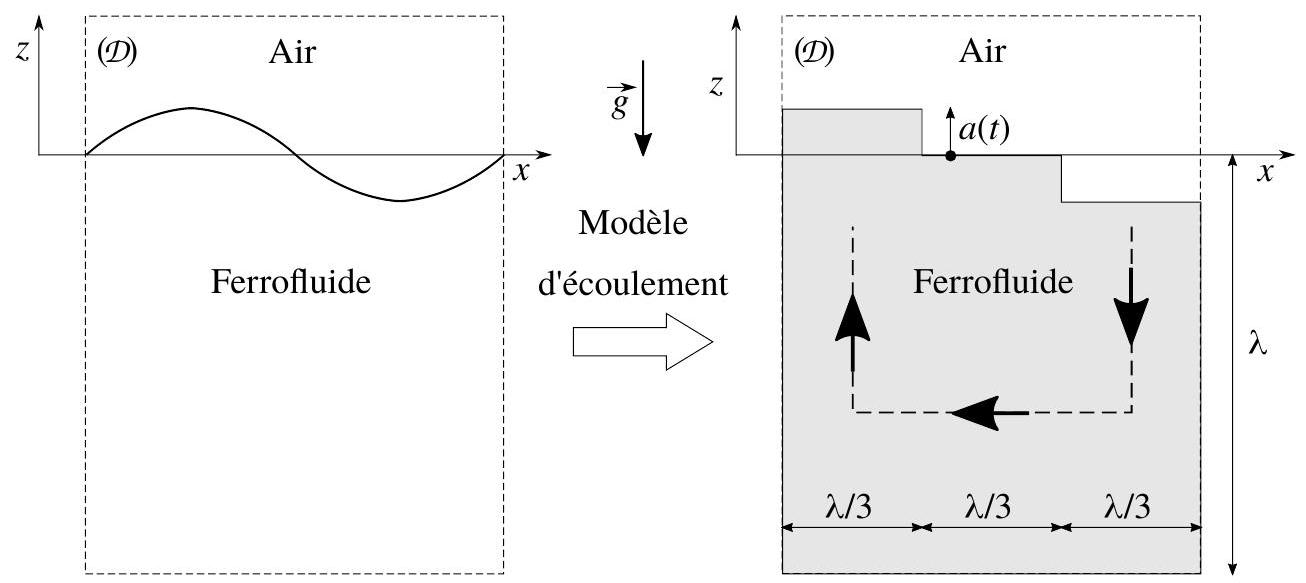Ce modèle est détaillé figure (3) où sont indiqués les paramètres géométriques introduits.
Figure 3 - Modèle d'écoulement simplifié en vue de déterminer la dépendance de son énergie cinétique avec les différents paramètres. Les flèches représentent les flux, essentiellement verticaux sur les parties gauche (formation d'une arche en bosse) et droite (formation d'une arche en creux) du domaine, essentiellement horizontal sur sa partie centrale (transfert de fluide). Le domaine ainsi modélisé est ici strictement fermé.
14. Exprimer la vitesse horizontale caractéristique .
15. Exprimer l'énergie cinétique associée au mouvement vertical du fluide, en fonction de et .
16. Exprimer l'énergie cinétique associée au mouvement horizontal du fluide, en fonction de et . Comparer à .
17. Déduire, des résultats obtenus dans cette partie, l'équation différentielle vérifiée par . On l'écrira sous la forme :

où est une grandeur caractéristique (choisie positive) que l'on exprimera en fonction de et .
18. En déduire l'expression de la pulsation , a priori complexe, introduite dans la relation (5).
19. Analyser le comportement dynamique de l'interface à travers ce résultat. Préciser pourquoi se révèle être une grandeur réelle.

5 Influence d'un champ magnétique.

Le ferrofluide est maintenant placé entre deux bobines de HelmHOLTZ créant un champ magnétique vertical, considéré comme uniforme sur le domaine étudié, et constant. Lorsque l'interface est déformée, l'interaction entre le milieu et le champ modifie localement les lignes de champ. C'est ce qu'illustre la figure (4). Nous admettons que cette modification locale des lignes de champ induit des forces dont l'énergie par unité de surface (de l'interface plane) associée s'exprime :
où est un coefficient positif traduisant les propriétés ferromagnétique du fluide et la perméabilité magnétique du vide. Afin d'alléger les calculs, nous poserons .
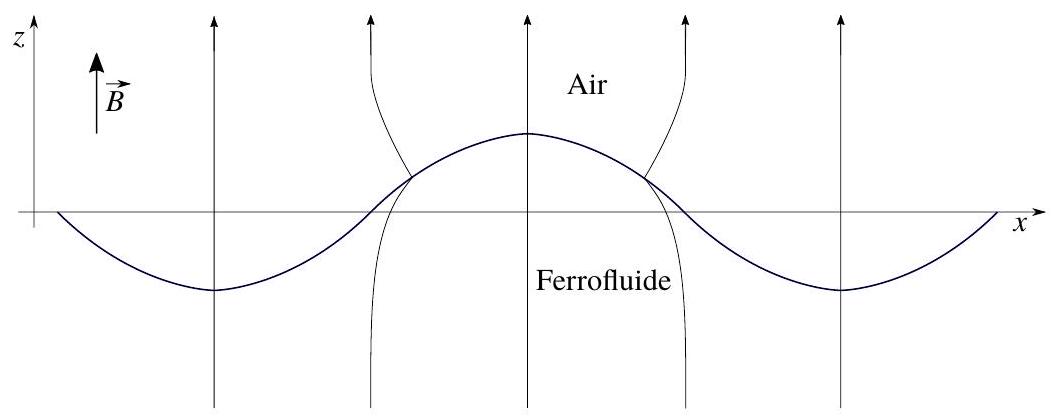
Figure 4 - Lignes de champ magnétique localement déformées par la courbure de l'interface du ferrofluide. Elles ont tendance à se concentrer au niveau des "bosses" et dépeupler les "creux". Cet effet est associé à une énergie de surface d'origine magnétique.
N.B. : Ici encore, tous les éventuels préfacteurs numériques qui apparaîtront dans les calculs seront substitués par 1 (voir le N.B. en fin de question (5)). Par exemple, on écrira .
20. Préciser, en justifiant la réponse donnée, la dimension du coefficient .
21. Proposer un argument en faveur de la forme de la dépendance de cette énergie par rapport à .
22. Exprimer l'énergie potentielle totale , somme des trois énergies potentielles, du domaine .
23. Nous posons, comme en question (11), . Vérifier que prend la forme :
ù
est l'énergie caractéristique introduite dans la relation (4). Préciser l'expression du paramètre en fonction de , et .
24. Proposer une interprétation physique du paramètre .
25. Représenter graphiquement la dépendance de la fonction avec pour trois valeurs du paramètre correspondant chacune à un comportement particulier de l'interface.
26. Déduire de cette étude graphique qu'il existe une valeur critique du paramètre , que l'on précisera, au-delà de laquelle l'interface devient instable.
27. Indiquer la valeur du premier nombre d'onde adimensionnalisé susceptible d'apparaître lorsque que l'on fait croître progressivement depuis la valeur nulle.
  • Comme dans la section (4), nous nous intéressons maintenant au comportement dynamique de l'interface. Nous écrivons alors l'amplitude sous la forme donnée par la relation (5) et cherchons à établir l'équation différentielle qu'elle vérifie en vue d'accéder à l'expression de la pulsation (a priori) complexe .
  1. En reprenant l'expression de l'énergie cinétique établie en réponse aux questions (15) et (16), exprimer l'énergie mécanique totale du domaine . Vérifier qu'elle conduit à la relation :
où est la pulsation caractéristique introduite dans la relation (6).
29. En déduire l'expression du carré de la pulsation en fonction de et .
30. Décrire les différents comportements dynamiques de l'interface observables selon la situation du paramètre par rapport à sa valeur critique .
31. En posant , et dans la limite , le temps caractéristique de croissance de l'amplitude du premier mode susceptible d'apparaître s'exprime par la relation :
Interpréter ce résultat.
  • La forme de l'interface photographiée figure (1) fut obtenue en augmentant progressivement le champ magnétique jusqu'à la formation de cette structure en "pics"
  1. Donner, en la justifiant, l'expression de la distance caractéristique séparant deux pics. Nous supposerons que les résultats obtenus sont qualitativement transposables en géométrie bidimensionnelle où et hors du régime des faibles déformations.
  • La longueur introduite dans la question (10) est appelée longueur capillaire. Elle représente la taille caractéristique d'une goutte en dessous de laquelle elle conserve une forme de calotte, lorsqu'elle est déposée sur une surface (du verre par exemple).
  1. À partir de constatations personnelles passées, donner un ordre de grandeur de pour de l'eau dans l'air.
  2. En supposant la valeur de la longueur capillaire pour les ferrofluides proche de celle de l'eau, comparer la prédiction du modèle établi au résultat expérimental présenté figure (1).
  3. L'étude qui a été conduite dans l'approche des faibles pertubations, prévoit, dès lors qu'une déformation de l'interface naît, une croissance illimitée de son amplitude . On constate pourtant, expérimentalement (figure (1)), qu'elle finit par se fixer sur une valeur déterminée . La prise en compte de termes non linéaires, dans l'expression de , modifie l'équation (9) qui devient :
ù
Préciser la méthode conduisant à la détermination de l'amplitude d'équilibre vers laquelle convergera.
En posant , exprimer dans la limite .
  • Les pics de ferrofluide peuvent également être obtenus en approchant progressivement une goutte de ferrofluide d'un aimant permanent dont l'axe Nord-Sud est vertical (voir figure (5)). La goutte finit alors pas se scinder en une série de pics individuels. La différence essentielle avec l'action d'un champ magnétique produit par des bobines de Helmholtz (cadre de l'étude réalisée) réside dans le fait que le champ créé par l'aimant présente un fort gradient vertical. Ce gradient donne naissance à une force volumique supplémentaire , au sein du fluide, qui l'attire vers l'aimant (placé sous l'échantillon de ferrofluide).
  1. En supposant uniforme dans le fluide, donner la nouvelle expression du nombre d'onde critique (défini question (27)), en fonction de et .
  2. Déduire de la figure (5) une estimation de .
  3. Donner alors l'ordre de grandeur du rapport (il sera utile d'utiliser la réponse à la question (32)).
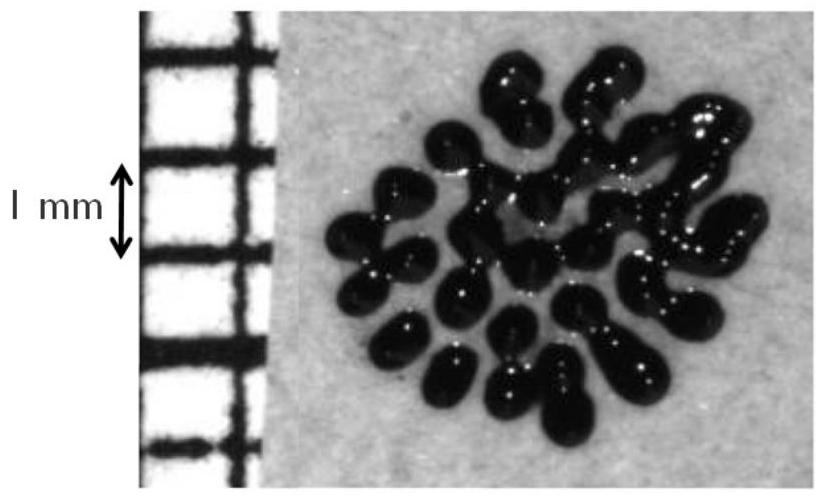
Figure 5 - Vue de dessus d'une goutte fractionnée en pics individuels par le champ créé par un aimant permanent (non visible) placé sous la goutte (de grande section par rapport à la surface de la goutte). Le ferrofluide est alors soumis à une force volumique liée à l'existence d'un gradient vertical de champ magnétique. La direction verticale ( ) est selon la normale au plan de la figure.

Partie Chimie Les nitrures de fer

La nitruration du fer est un procédé de surface qui permet d'en améliorer certaines propriétés physico-chimiques. Ce type de traitement de surface s'est développé au début du XX siècle pour connaître plusieurs évolutions en terme de procédé (en phase gaz, phase liquide ou plasma).

1 Composition des nitrures de fer.

1.1 Étude du diagramme binaire.

Le diagramme de phase fer-azote est donné sur la figure (1). Sauf mention contraire, les variétés allotropiques de nitrure de fer pourront être notées (i)-FeN où indique la nature de la phase.
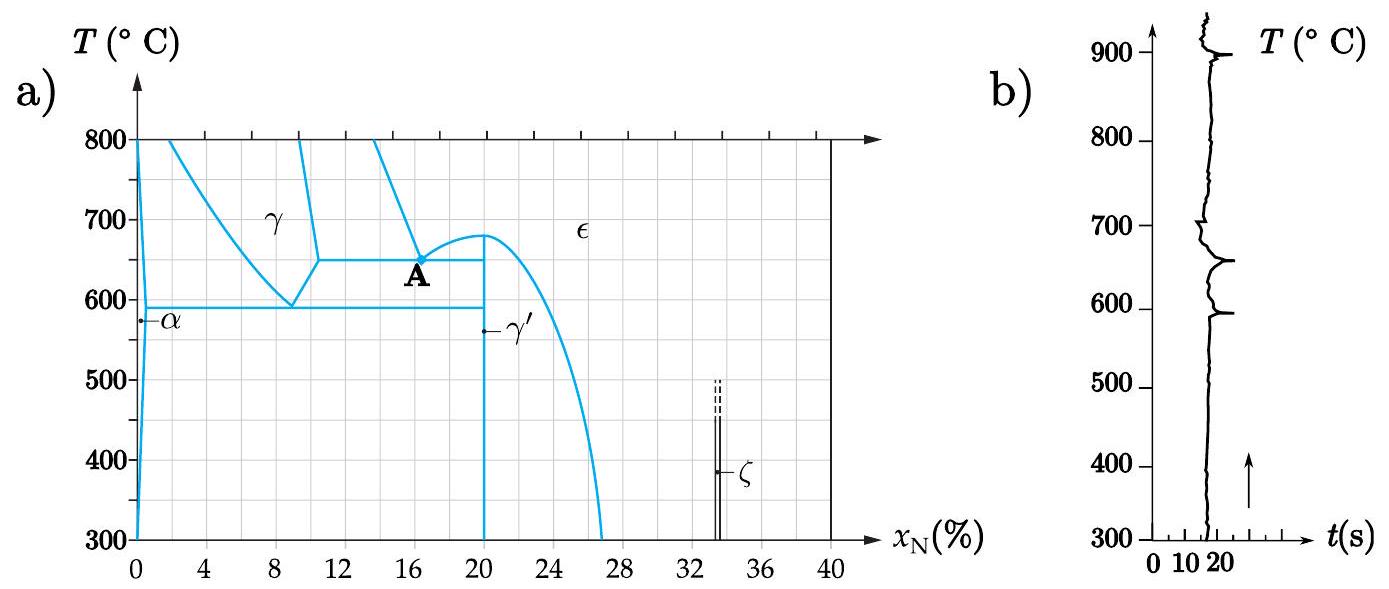
Figure 1 - a) Diagramme de phase simplifié du système fer-azote en fraction molaire. Les domaines monophasiques sont indiqués. b) Courbe d'échauffement pour un nitrure de fer inconnu. Le temps indiqué correspond au temps nécessaire pour élever la température de à apport d'énergie constant.
  1. Donner la composition approchée de la phase ( )- FeN et ( )- FeN sous la forme avec et entiers.
  2. Donner l'équation de la réaction chimique correspondant à la transformation lors du refroidissement au point indiqué sur la figure (1). Indiquer la différence entre ce point, appelé "eutectoïde", et un point eutectique.
  3. Donner une gamme de composition possible pour le nitrure de fer utilisé dans la figure (1) b). Justifier.

1.2 Micro-structure des nitrures de fer.

La structure cristalline de la phase -FeN est telle que les atomes de fer y occupent une structure cubique face centrée de paramètre de maille .
4. Représenter la maille des atomes de fer dans la structure . Indiquer un site tétraédrique et un site octaédriques puis dénombrer chaque type de site.
5. Calculer la taille des sites octaédriques et tétraédriques dans la maille -FeN.
6. En déduire si l'azote forme une solution solide d'insertion, ou de substitution. Indiquer la position des atomes d'azote et proposer une structure cristallographique pour cette phase.

2 Nitruration en phase gaz.

2.1 Diagramme de Lehrer.

En pratique, la nitruration se fait sur du fer- entre 500 et en présence d'un mélange d'ammoniac, de diazote et de dihydrogène à pression atmosphérique.
Pour le nitrure , il est possible d'utiliser un modèle de mélange idéal où les deux constituants sont les atomes d'azote occupant le réseau de sites interstitiels (notés ) et les sites interstitiels restés vacants (notés V ). Ce processus correspond à l'équilibre suivant :
La fraction molaire d'azote en sites interstitiels est notée .
7. Exprimer les potentiels chimiques de l'azote interstitiel et des sites interstitiels en fonction de leurs potentiels chimiques standard et de leurs fractions molaires respectives puis en fonction des potentiels chimiques standard et uniquement de la fraction molaire d'azote en sites interstitiels .
8. Donner la relation liant les potentiels chimiques de et à l'équilibre thermodynamique.
Pour la suite, on définit le potentiel de l'azote dissocié en phase gaz comme .
9. Déduire des questions précédentes une expression de en fonction des potentiels chimiques standard et de la fraction molaire d'azote en site interstitiels à l'équilibre notée yéq.
Le potentiel chimique est imposé par la réaction entre le diazote, le dihydrogène et l'ammoniac.
10. Écrire l'équation de réaction entre les trois composés chimiques. En déduire une relation à l'équilibre chimique entre , le potentiel chimique du dihydrogène et celui de l'ammoniac.
11. Montrer que est une fonction uniquement de grandeurs standard et de la grandeur appelée potentiel de nitruration.
12. Montrer qu'il est possible d'obtenir l'expression de yéq en fonction des potentiels chimiques standard et de .
Un travail similaire permet d'obtenir une expression de l'activité de l'azote dans les différentes phases en fonction de et de grandeurs thermodynamiques standard. Il est alors possible de délimiter des zones correspondant aux domaines où une des phases est la plus stable. Il s'agit du diagramme de Lehrer (figure (2)).
13. Proposer une limite du modèle de mélange idéal qui le rend inutilisable pour les phases et .
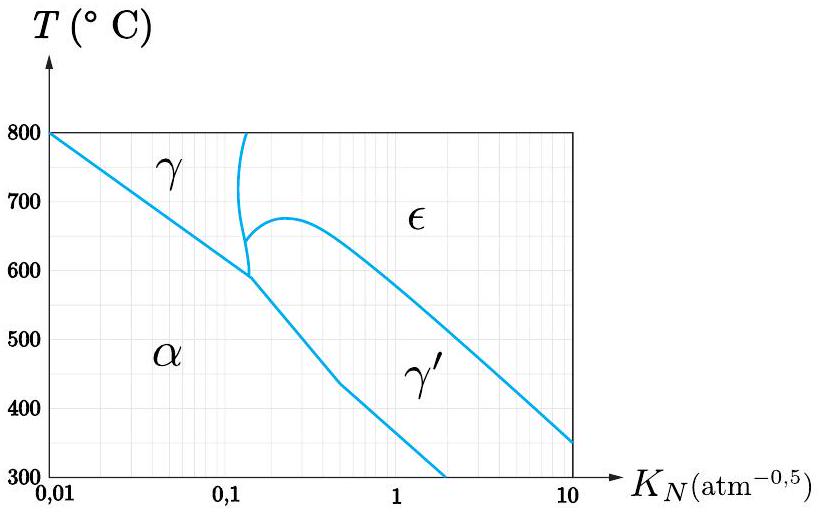
Figure 2 - Diagramme de Lehrer donnant la composition de la phase en équilibre en fonction de la température et du potentiel de nitruration exprimé en . L'échelle des abscisses est logarithmique.

2.2 Résultats expérimentaux.

La composition finale du système est inhomogène et peut être caractérisée par spectroscopie. Une coupe du matériau nitruré est donnée sur la figure (3) et le profil de concentration en azote est donné sur la figure (4).
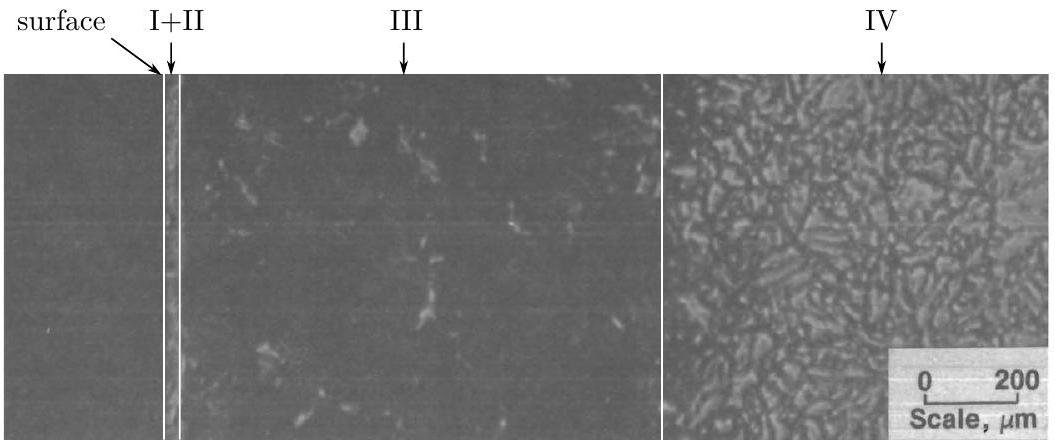
Figure 3 - Allure de la coupe d'une plaque de fer ayant subi une opération de nitruration vue en microscopie. Les zones I et II forment ce que l'on appelle la couche "composite" et la zone III est appelée couche diffusive.
  1. Donner la variété allotropique majoritaire dans les zones I, II, III et IV. On rappelle que les différentes variétés allotropiques sont données sur la figure (1).
  2. Expliquer si le potentiel de nitruration de la figure (4) a) est compatible avec le diagramme thermodynamique de Lehrer donné sur la figure (2).
Pour des aciers - qui sont des alliages fer-carbone, il est possible d'obtenir en contact les phases et sans obtenir de phase .
16. Justifier si ces observations sont compatibles avec les différents diagrammes binaires donnés pour les nitrures de fer (figures (1) et (2)).
17. À partir des données de la figure (4) b), calculer un ordre de grandeur pour le coefficient de diffusion de l'azote dans la zone III.
18. Donner l'intérêt de l'opération de revenu qui consiste à élever de nouveau la température de l'échantillon.
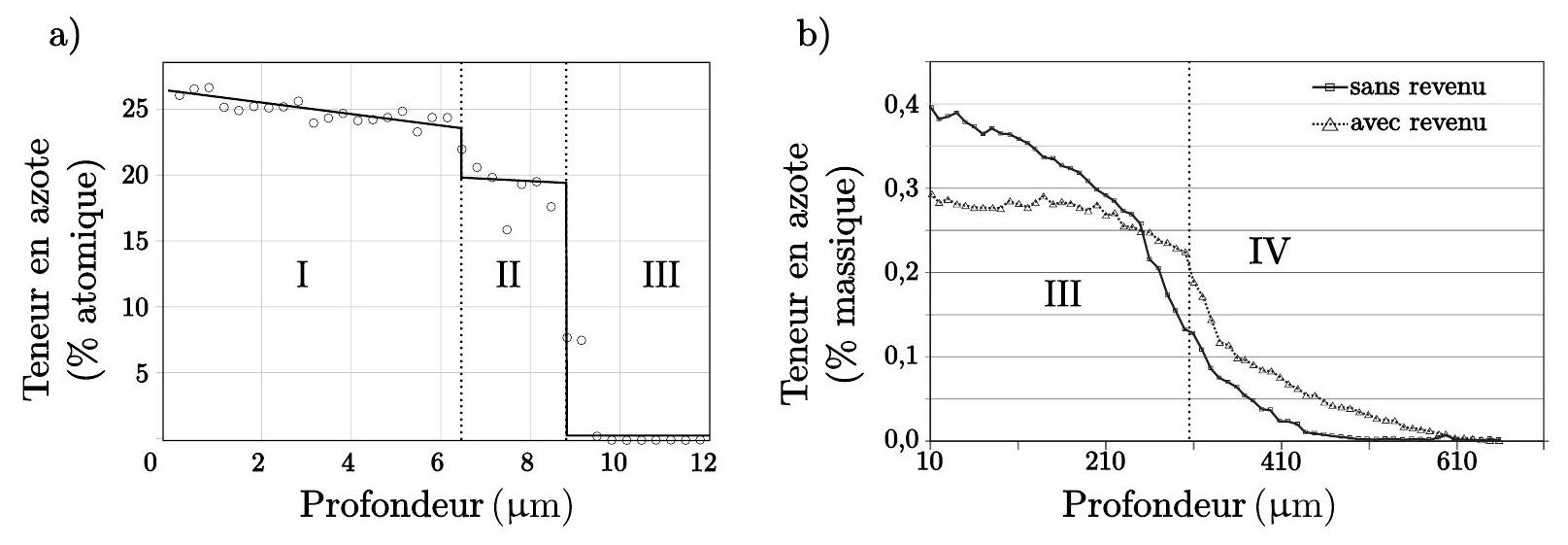
Figure 4 - Profils de concentration en azote en fonction de la profondeur selon une coupe. a) à gauche, à proximité de la surface pour une nitruration à pendant 120 minutes et un potentiel de nitruration de . b) à droite, plus loin de la surface pour une nitruration à pendant 24 h pour un potentiel de nitruration de .

2.3 Cinétique de nitruration.

Pour suivre la cinétique de nitruration, il est possible de suivre la prise de masse d'un échantillon dans un réacteur ouvert. Pour cela, des nano-cristaux de fer sont placés sur une balance, le tout étant dans une enceinte de réacteur ouvert. La géométrie de l'ensemble étant relativement complexe, il est nécessaire d'en mesurer le volume avant de pouvoir effectuer des mesures. Pour cela, une expérience de dilution du dihydrogène dans le diazote est menée - il n'y a pas de réaction chimique lors de la réaction. La fraction molaire en sortie est alors analysée. Pour un réacteur parfaitement agité idéal, cette dernière suit une loi de vitesse avec le temps de passage dans le réacteur.
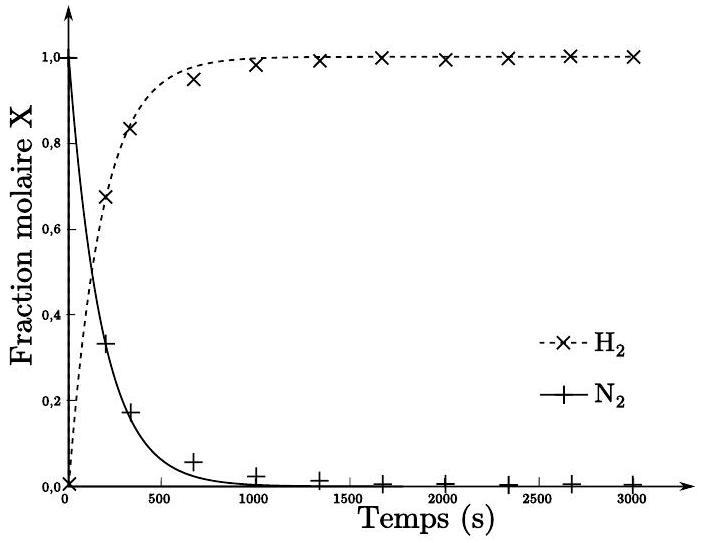
Les données obtenues pour un débit volumique sont données sur la figure (5). Les courbes de prises de masse à différentes valeurs de ou débits volumiques sont données sur la figure (6).
Figure 5 - Courbes d'évolution de la concentration lors de la dilution avec un débit volumique de . La courbe en pointillés correspond à la fraction molaire en hydrogène et celle en traits pleins à celle en diazote.
  1. Avec la loi de vitesse, donner le lien entre le temps nécessaire pour diluer d'un facteur 2 le diazote, noté , et le temps de passage .
  2. À partir des données, déduire la valeur du volume du réacteur. Indiquer également quelle autre indication sur le réacteur est fournie par l'expérience.
  3. À l'aide de la figure (2), donner la phase thermodynamiquement stable pour les trois potentiels de nitruration de la figure (6). Expliquer l'intérêt de ces trois mesures.
  4. À partir des données, proposer les phénomènes physico-chimiques cinétiquement déterminants (production d'ammoniac, diffusion, germination de la phase , enrichissement de la phase , décomposition de l'ammoniac) pour et (figure (6) a)).
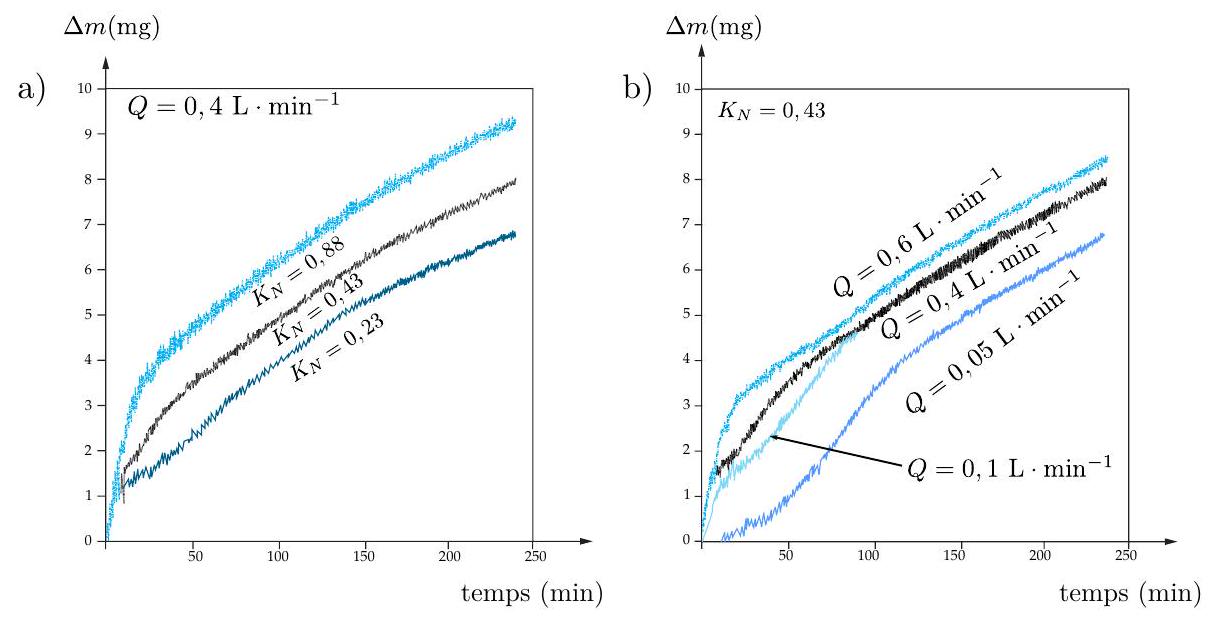
Figure 6 - Courbes de prises de masse en fonction du temps à . a) pour différentes valeurs de à gauche et b) différents débits volumiques à droite. Le potentiel de nitruration est toujours exprimé en .
  1. De même, proposer trois phases cinétiques distinctes parmi celles citées à la question précédente pour la courbe correspondant à .

3 Nitruration en milieu non aqueux.

3.1 Diagramme .

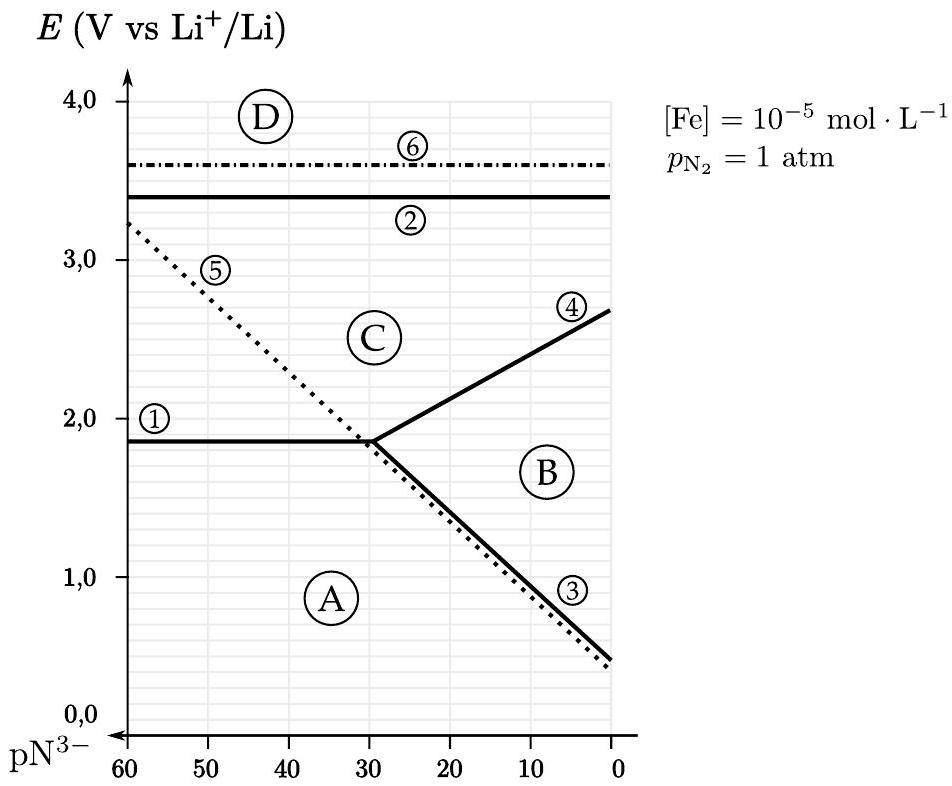
La nitruration peut également se faire en milieu liquide. L'électrolyse dans un sel fondu (liquide où les ions sont dissociés) fait partie des différentes techniques utilisées. Le diagramme est donné sur la figure (7). Les espèces (s), et sont représentées pour le fer.
Figure 7 - Diagramme - dans le milieu à 723 K . Le couple de référence choisi est le couple . Toutes les frontières en traits pleins concernent le fer (1,2,3,4). Le trait en pointillé (5) concerne le couple . Le trait en pointillés alternés (6) concerne le couple . La concentration du tracé est et la pression en diazote est la pression atmosphérique.
  1. Attribuer les espèces sur la figure (7).
  2. Exprimer le potentiel standard du couple sous forme littérale à l'aide des données thermodynamiques fournies en annexe.
  3. Donner l'équation de la frontière (3) sur la figure (7) sous forme littérale .
  4. Mesurer la valeur de la pente (3), commenter sa valeur.
  5. Expliquer à quelle opération mathématique sur le diagramme correspond le fait d'exprimer les potentiels par rapport au couple au lieu de .
  6. Donner les avantages et inconvénients liés au fait de travailler en milieu non aqueux. Justifier.

3.2 Électrolyse.

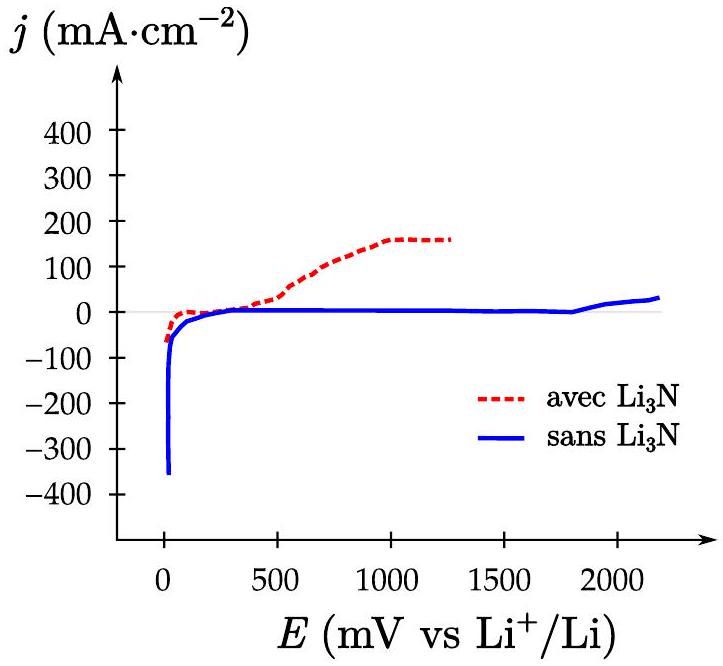
L'électrolyse est menée à 723 K dans le sel fondu en présence de nitrure de lithium entre une électrode d'aluminium et une électrode de fer, la différence de potentiel appliquée est de 800 mV . Les courbes courant-potentiel sur l'électrode de fer sont données sur la figure (8).
Figure 8 - Courbe courant-potentiel sur l'électrode de fer. La courbe en trait plein correspond à la courbe en l'absence de , la courbe en pointillés est la courbe obtenue après ajout de nitrure de lithium .
  1. Faire un schéma d'un montage utilisé pour tracer les courbes courant-potentiel en milieu aqueux.
  2. Expliquer quelles sont les différentes réactions d'oxydation observées sur l'électrode de fer en l'absence et en présence de nitrure de lithium .
  3. Indiquer quelle électrode est l'anode, quelle électrode est la cathode ainsi que leurs polarités respectives.
  4. Indiquer les réactions qui se déroulent aux électrodes lors de l'électrolyse. En déduire l'équation bilan de l'électrolyse.
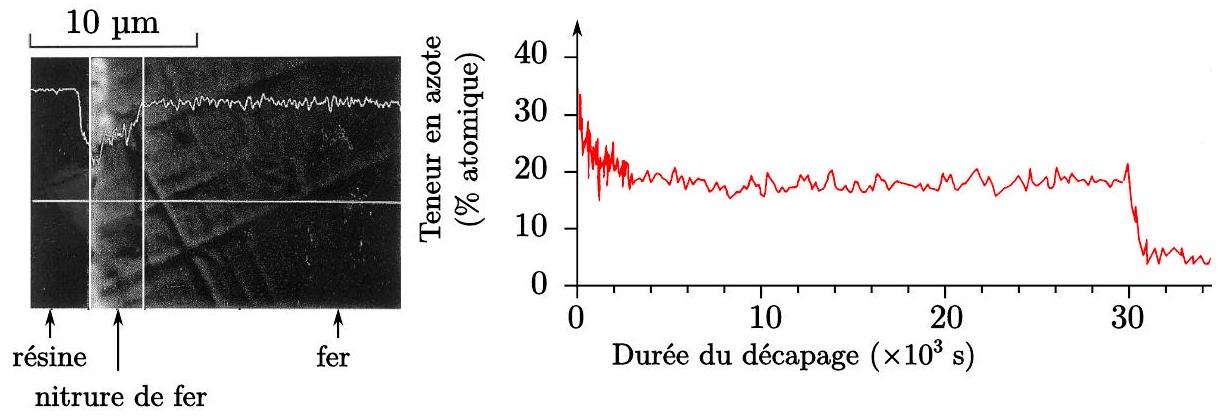
Comme précédemment, il est possible d'analyser la plaque obtenue par spectroscopie. La technique utilisée permet de caractériser les surfaces. L'analyse est faite en continu pendant que l'électrode de fer subit une attaque acide. Le rythme de dissolution lié au décapage à l'acide est constant et de l'ordre de . La teneur en azote après électrolyse pendant 30 minutes en présence de nitrure de lithium avec une tension de 800 mV est donnée sur la figure (9).
Figure 9 - À gauche, vue par microscopie d'une coupe de l'électrode de fer obtenue. À droite, teneur en azote mesurée à la surface de l'électrode de fer en fonction de la durée de l'attaque acide.
  1. Caractériser la composition de la surface de l'électrode (variétés allotropiques par zone et épaisseur de chacune de ces zones).
Le procédé n'est pas assez performant pour obtenir une couche protectrice suffisamment épaisse. Pour améliorer le processus, en gardant les mêmes conditions opératoires, il est possible de réaliser une électrolyse pulsée. Le potentiel d'électrolyse adopté est un signal rectangulaire pour lequel une tension de 800 mV est appliquée pendant 10 s puis une différence de potentiel de 1800 mV est appliquée pendant 1 s . Le cycle est répété pendant une heure. Une vue par microscopie de l'électrode de fer traitée avec ce procédé est donnée sur la figure (10).
Figure 10 - Allure en microscopie d'une coupe de l'électrode ayant subi l'électrolyse pulsée.
  1. Expliquer les avantages et les inconvénients liés à l'électrolyse pulsée pour la nitruration du fer.
  2. À l'aide des différentes données, proposer une explication microscopique qui explique la différence de résultat entre les deux types d'électrolyses.

Données.

  • ;
  • ;
  • ;
  • pour
  • 1 jour
  • ;
  • Potentiel standard du couple du lithium par rapport à l'ESH à
Couple
0,382 3,626 3,304 3,390 2,238
TABLEAU 1 - Potentiels standard par rapport au couple à 723 K exprimés en volts.
Élément Fe N
Rayon atomique 126 71
Tableau 2 - Rayons atomiques du fer et de l'azote en picomètres.
    1. Le plus souvent formées, en grande proportion, d'oxyde de fer.
  2. N.B. : Afin de conserver la cohérence des calculs avec cette modélisation, tous les éventuels préfacteurs numériques qui apparaîtront seront remplacés par 1 (voir le N.B. en fin de question (5)). Par exemple, la vitesse verticale caractéristique sera écrite .
ENS Physique Chimie L PC 2018 - Version Web LaTeX | WikiPrépa | WikiPrépa