J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Physique Chimie L PC 2023

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2023
Filière
PC
Matière
Physique Chimie
X-ENS PCX-ENS 2023PC Physique ChimiePhysique Chimie 2023
2025_09_04_e50383471cfd4daf73ecg

ÉCOLE NORMALE SUPÉRIEURE DE LYON

CONCOURS D'ADMISSION 2023

VENDREDI 21 AVRIL 2023
08h00-13h00
FILIÈRE PC - Épreuve
PHYSIQUE-CHIMIE (L)
Durée : 5 heures
  • L'utilisation de calculatrices n'est pas autorisée pour cette épreuve.
  • Les parties relatives à la chimie et à la physique doivent être rédigées sur des copies distinctes, et en tête desquelles doit être mentionné "Chimie" ou "Physique".
  • Les copies doivent être numérotées continûment, sur l'ensemble des deux parties.
Cette épreuve comprend deux parties indépendantes. La première concerne la physique et propose une étude du phénomène d'effusion gazeuse. La seconde est dédiée à la chimie et s'intéresse à quelques aspects de la chimie du bore.
Le barème est réparti à poids égal sur les parties physique et chimie. Il est conseillé de ne pas consacrer plus de deux heures et trente minutes à chacune d'elles.
Les résultats des applications numériques, ainsi que les ordres de grandeur, seront donnés avec un chiffre significatif.
Les références des questions abordées devront être indiquées de façon visible et claire.

Partie Physique : Effusion gazeuse

Nous notons l'intégrale généralisée suivante :
Ses quatre premières valeurs sont les suivantes :
Cette étude sera conduite dans le cadre suivant :
  • La pesanteur n'est pas prise en compte.
  • Le gaz est monoatomique et parfait.
  • Sa température reste fixée par un thermostat.
Nous nous proposons d'étudier le phénomène d'effusion gazeuse. Ce phénomène se rapporte à l'échappement d'un gaz à travers un orifice percé dans la paroi de l'enceinte contenant ce gaz. Le régime d'échappement est effusif lorsque le trou est tel que les atomes (ou molécules) le franchissent sans subir de collision entre eux (elles) (hypothèse notée ). Les atomes (ou molécules) passent alors à travers le trou comme un ballon passerait à travers une fenêtre ouverte, la condition de son passage ne dépendant que de la direction de son lancer. Cette analogie suggère que nous devons nous placer au niveau atomique et adopter un point de vue statistique pour étudier ce phénonème.
Cette étude comprend quatre parties. La première porte sur des considérations générales. La seconde est consacrée à l'étude de la distribution des vitesses des atomes d'un gaz à l'équilibre thermodynamique. La troisième s'intéresse à l'expression du flux effusif. Enfin, la quatrième propose quelques applications. Les deux premières parties sont indépendantes. La troisième est liée à la deuxième et la quatrième à la troisième.
Les réponses aux questions, en particulier lorsqu'elles relèvent de considérations qualitatives, devront être systématiquement argumentées. En outre, elles devront être rédigées de façon claire et concise.

Notations, données et formulaire - Hypothèses générales.

Les grandeurs qui apparaissent dans la liste ci-dessous seront introduites dans la suite (certaines sont définies sur la figure (1)). Les valeurs numériques sont données avec un chiffre significatif.
  • Constante de Boltzmann :
  • Température de thermalisation :
  • Masse d'un atome (hélium) du gaz :
  • Volume d'une enceinte (supposée cubique) :
  • Aire de la section de l'orifice d'effusion (trou circulaire)
Nous notons l'intégrale généralisée suivante :
Ses quatre premières valeurs sont les suivantes :
  • Ses évolutions sont considérées comme étant quasi-statiques. Cela signifie, en particulier, que les gran- deurs thermodynamiques intensives se rapportant au gaz seront considérées, à tout instant, comme uniformes dans chacune des enceintes.

1 Considérations préliminaires.

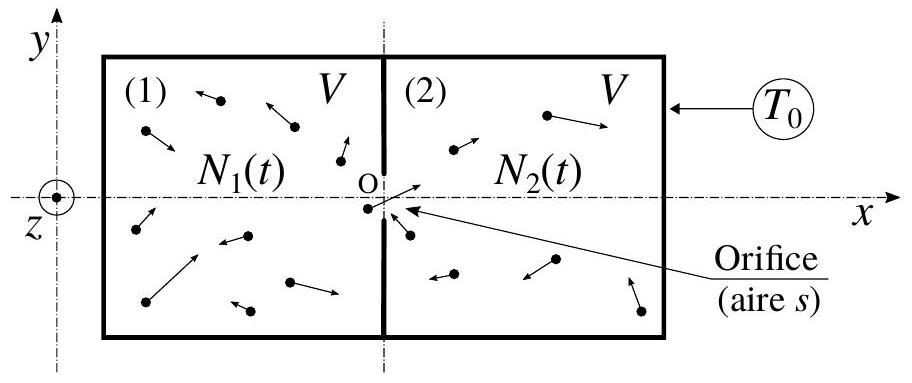
Nous considérons deux enceintes cubiques identiques, de volume , pouvant échanger des atomes de gaz à travers un orifice circulaire d'aire percé dans leur paroi commune. Les enceintes sont en contact avec un thermostat qui fixe leur température et celle du gaz à . Ce système est illustré sur la figure (1), à un instant donné. Chacun des atomes (représentés par des points) est alors animé d'une certaine vitesse représentée par une flèche. La vitesse des atomes est répartie selon une certaine distribution continue, à la fois selon sa direction et sa norme.
Figure 1 - Deux enceintes cubiques identiques (1) et (2), de volume , échangeant des atomes de gaz par l'intermédiaire d'un "petit" orifice d'aire . Le gaz, dans chacune des enceintes, est à la température supposée uniforme et constante.
Nous notons et les nombres d'atomes occupant respectivement les enceintes (1) et (2), à l'instant . La situation initiale est telle que et .
  1. Rappeler la définition du "libre parcours moyen", que nous noterons , d'un atome (ou d'une molécule) dans un gaz.
  2. L'échappement du gaz par un trou s'effectue en régime effusif à condition que l'hypothèse, notée dans la présentation de l'étude, soit vérifiée. Indiquer quelle condition l'aire de la section du trou doit alors satisfaire.
  3. Représenter, qualitativement, l'allure de l'évolution temporelle de chacun des nombres d'atomes et .
  4. Préciser de quelles grandeurs le temps caractéristique de ces évolutions dépend, a priori.
Indiquer s'il apparaît alors possible d'accéder à la forme de la dépendance de vis-à-vis de ces grandeurs, sur la seule base d'une analyse dimensionnelle.
5. Analyser le caractère réversible ou irréversible de ces évolutions.

2 Distribution des vitesses des atomes du gaz.

Dans cette partie, nous nous plaçons dans le cas général d'un gaz (monoatomique) contenu dans une enceinte thermalisée à la température , à l'équilibre thermodynamique. Nous notons , où , une vitesse.
La probabilité élémentaire , par unité de volume, que la vitesse d'un atome appartienne à l'intervalle , s'exprime par la relation suivante :
ù
Nous notons, parallèlement :
ù
Par ailleurs, la moyenne d'une grandeur , sur un domaine de vitesses , pondérée par la distribution de probabilité , est définie par l'égalité suivante :
  1. Indiquer la condition que la constante doit satisfaire. En déduire l'expression de cette constante en fonction de et du produit .
  2. Représenter l'allure graphique de la fonction pour deux températures et (en correspondance, sur le même repère). Commenter ces tracés.
  3. La valeur moyenne s'exprime par une relation qui prend la forme suivante :
Exprimer la fonction (on conservera la constante sans développer son expression). Représenter son allure graphique.
9. Exprimer les moyennes et en fonction de .
Commenter chacun de ces résultats.
Calculer l'ordre de grandeur de .

3 Expression du flux effusif.

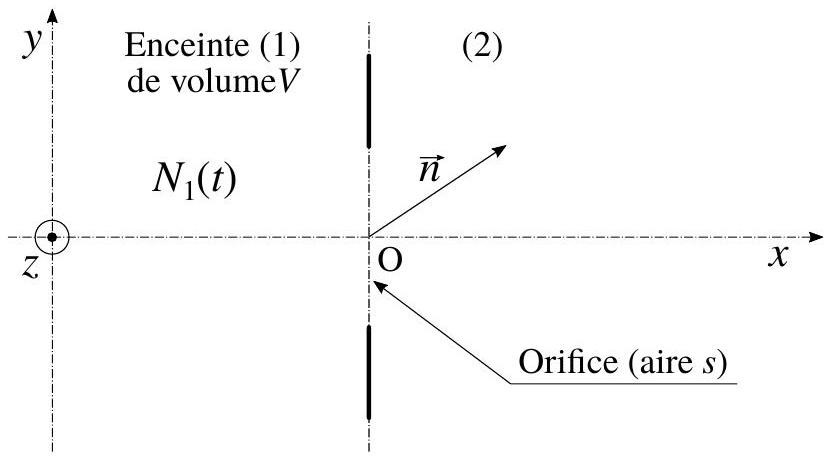
Il s'agit d'exprimer le nombre d'atomes sortant de l'enceinte (1) au profit de l'enceinte (2), par unité de temps (nous ne nous préoccupons pas, dans cette section (3), des atomes qui franchissent le trou dans l'autre sens). Choisissons, arbitrairement, un domaine élémentaire de vitesse où ( 1 et ). La figure (2) place le vecteur dans le contexte de l'étude (afin de simplifier cette figure, est représenté dans le plan .
Figure 2 - Vecteur unitaire ( ), choisi arbitrairement, définissant une direction et un sens particuliers de la vitesse des atomes dans l'enceinte.
  1. Reproduire le schéma de la figure (2). Y représenter le volume élémentaire dD contenant l'ensemble des atomes qui s'échapperont de l'enceinte (1), par le trou, entre les instants et , et dont la vitesse est égale à (à près). Exprimer puis le nombre élémentaire d'atomes qu'il contient. On exprimera la grandeur en fonction de et .
  2. En prenant en compte la distribution des vitesses définie par l'équation (3), exprimer le nombre moyen d'atomes sortant de l'enceinte (1), par unité de temps. Nous notons cette grandeur et l'écrivons sous la forme suivante :
Exprimer la constante positive en fonction de et .
N.B. : Dans la suite, on utilisera directement la relation (7), en conservant le paramètre sans développer son expression.
12. Calculer l'ordre de grandeur de dans le cas où . (il manquait la valeur du volume )
13. Commenter ce résultat, notamment au regard des hypothèses adoptées.
14. Nous souhaitons que le libre parcours moyen des atomes vérifie l'inégalité suivante :
En déduire l'expression de la pression que le gaz d'atomes, dans l'enceinte, ne doit pas excéder. Après avoir fixé l'ordre de grandeur de estimer celui de la pression .
Donnée : Le libre parcours moyen d'une particule, en mouvement au sein de ses semblables, est lié à la section de ces particules et à leur concentration numérique (nombre par unité de volume) par la relation suivante (à un éventuel préfacteur numérique près) :

4 Dynamique d'échange d'atomes.

Cette partie met en œuvre l'équation (7), dans quelques situations particulières.

4.1 Système fermé formé de deux enceintes.

Nous nous plaçons ici dans la situation décrite dans la partie (1) où deux enceintes identiques, thermalisées à la température , échangent des atomes par l'intermédiaire d'un "petit" orifice (se reporter à la figure (1)).
15. Établir le système d'équations différentielles vérifié par les nombres d'atomes et contenus dans chacune des enceintes.
16. Exprimer la solution correspondant aux conditions initiales et .
17. Il est possible de tirer parti du phénomène d'effusion gazeuse pour isoler, au moins partiellement, un composant particulier d'un gaz. Pour illustrer cette application, nous supposons que le gaz est formé de deux types d'atomes (a) et (b) et qu'il est initialement entièrement contenu dans l'enceinte (1). Il s'agit de recueillir, dans les meilleures conditions, un gaz enrichi (ou appauvri) de l'un de ses composants.
Expliquer sur quelle propriété du phénomène d'effusion cette application repose.
Justifier qu'il existe un instant optimal pour arrêter l'effusion. Exprimer le temps correspondant.
Indiquer dans quelle situation concrète cette technique de séparation a été, ou peut être, utilisée.
N.B. : Il s'agit, dans cette question (17), de mettre en place quelques étapes qu'il conviendra de présenter clairement, avec les éventuelles notations introduites.

4.2 Système ouvert formé de deux enceintes.

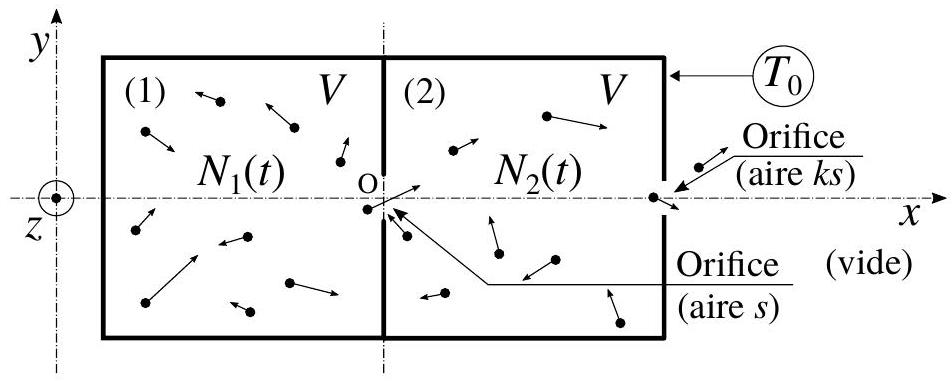
La situation est la même que celle décrite dans l'étude précédente à la différence près que l'enceinte (2) est ici percée d'un second trou (se reporter à la figure (3)). Ce trou, d'aire , donne sur le milieu extérieur que nous supposons être le vide. Nous notons la constante de temps faisant intervenir l'aire du trou de communication entre les deux enceintes (identiques) et celle faisant intervenir l'aire (se reporter à l'équation (7)).
Figure 3 - Deux enceintes cubiques identiques (1) et (2), de volume , échangeant des atomes de gaz par l'intermédiaire d'un "petit" orifice d'aire . La seconde enceinte est percée d'un second trou d'aire , donnant sur l'extérieur (le vide). Le gaz est uniformément à la température .
  1. Établir le système d'équations différentielles, paramétré par les seules constantes et , vérifié par les nombres d'atomes et contenus dans chacune des enceintes.
  2. Former l'équation différentielle vérifiée par la fonction (paramétrée par les seules constantes et .
  3. Exprimer le facteur de qualité associé à cette équation différentielle. Analyser ce résultat.
  4. Nous notons et les racines (qu'il est inutile de calculer) du polynôme caractéristique associé à l'équation différentielle vérifiée par la fonction (se reporter à la question (19)). Sur la base d'arguments physiques (c'est-à-dire non issus de calculs), indiquer pourquoi ces racines sont nécessairement, d'une part réelles, d'autre part négatives.
  5. Exprimer la solution correspondant aux conditions initiales et 0 , paramétrée par les constantes et . On ne cherchera pas à établir l'expression des racines et .
  6. La figure (4) représente l'évolution du rapport vis-à-vis de la variable , pour trois valeurs et , du paramètre .
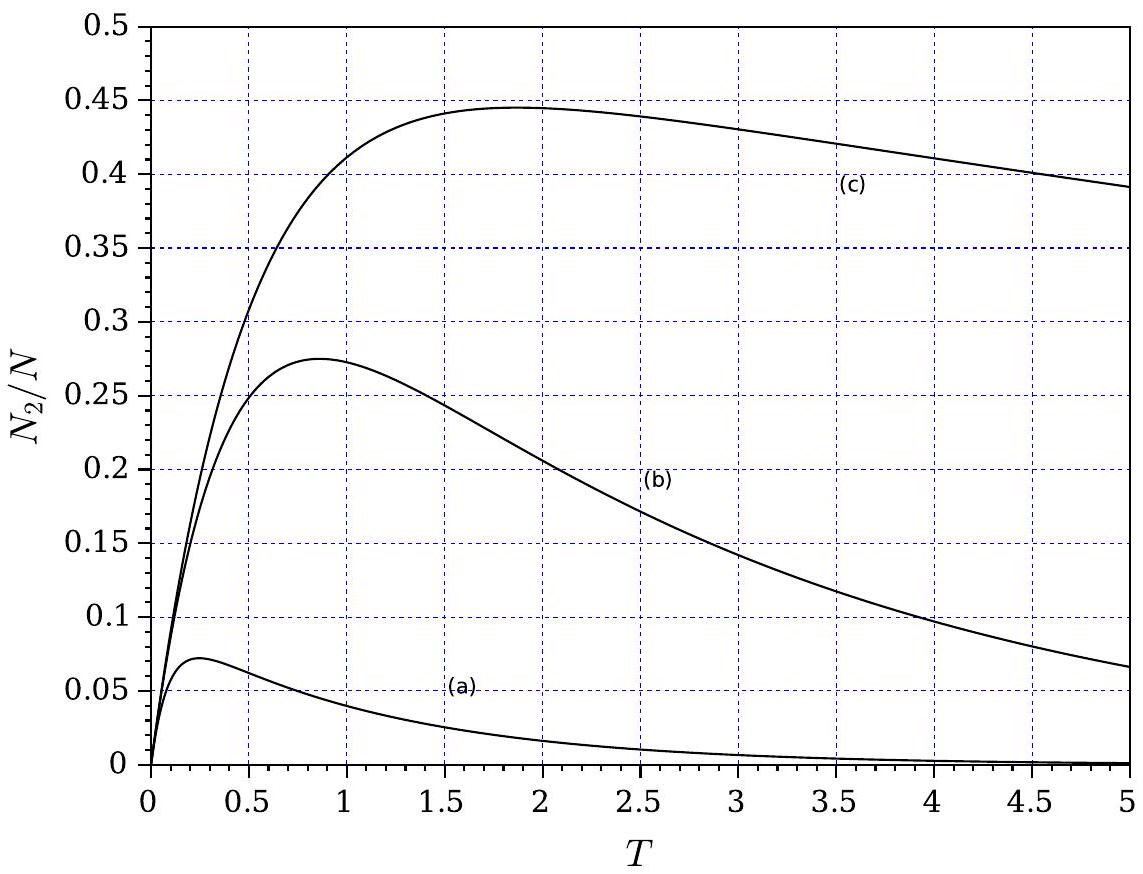
Figure 4 - Évolution du rapport vis-à-vis de la variable , pour trois valeurs et , du paramètre .
Indiquer la correspondance, en la justifiant, entre les références (a), (b) et (c) des tracés et les trois valeurs de .
Analyser le comportement de ces évolutions aux temps courts ( ). Interpréter ce résultat.
24. Nous considérons la situation pour laquelle . Représenter, qualitativement (c'est-àdire qu'aucun calcul n'est à effectuer), l'allure de l'évolution de vis-à-vis de la variable , en correspondance avec celle de . On commentera les tracés proposés.
25. Indiquer comment, expérimentalement (c'est-à-dire en pratique), l'évolution temporelle du nombre d'atomes dans une enceinte (i) peut être suivie.

4.3 Système formé d'une série d'enceintes.

Le système étudié est maintenant constitué d'une suite de enceintes identiques (cubiques, de côté ). Chaque enceinte (hormis les première et dernière) peut échanger des atomes avec ses deux voisines par l'intermédiaire d'un "petit" trou. Tous les trous sont identiques, de section notée . Nous notons le nombre d'atomes occupant l'enceinte ( ), à l'instant . Cette partie met en œuvre l'équation (7).
26. Établir l'équation différentielle reliant et , pour .
  • Nous supposons dès lors que . En vue d'un passage à la limite continue, nous écrivons la variable discrète de la façon suivante :
ù
Nous supposons que la fonction peut être développée dans le voisinage de toute abscisse.
27. Établir l'équation aux dérivées partielles vérifiée par la fonction . Commenter ce résultat.
28. Indiquer à quelle condition, portant sur la suite ( ) des nombres d'atomes, le passage à la limite continue que nous avons effectué reste justifiable.
29. Nous supposons que le système formé de l'ensemble des enceintes est fermé (c'est-à-dire qu'il n'y a aucune fuite vers l'extérieur). À l'instant intial, la première enceinte contient atomes et les autres sont vides (nous ne tiendrons pas compte du fait que ces conditions intiales peuvent ne pas satisfaire la condition établie en réponse à la question (28)).
Représenter qualitativement l'allure graphique de l'évolution temporelle de la fonction représentant le nombre d'atomes occupant l'enceinte d'abscisse (dans la limite continue). Nous considérerons que cette enceinte se situe au milieu de la chaîne, ou dans son voisinage. On enrichira ce tracé d'éventuelles données.

4.4 Analogie électrocinétique.

Il s'agit d'établir une analogie, dans le domaine de l'électrocinétique, d'un système formé de deux enceintes en communication par l'intermédiaire d'un orifice. L'une peut être, ou non, en communication avec l'extérieur par l'intermédiaire d'un second trou. Ces deux situations sont illustrées sur les figure (1) et (3). Cette partie met en œuvre, en particulier, l'équation (7).

N.B. : Toutes les réponses données devront être clairement argumentées.

  1. Indiquer, sur la base d'une construction rigoureuse, quels sont les équivalents, pour le système , d'une charge électrique , d'un courant , d'un potentiel électrique é, d'une résistance et d'une capacité . On donnera l'expression de chacun de ces équivalents. En particulier, on exprimera la "résistance effusive" en fonction de et (aire de la section d'un trou).
  2. Représenter, par un schéma, l'analogue électrique du système fermé formé de deux enceintes en communication par l'intermédiaire d'un trou (se reporter à la figure (1)).
  3. Représenter, par un schéma, l'analogue électrique du système formé de deux enceintes en communication par l'intermédiaire d'un trou (aire ), l'une étant en communication avec l'extérieur (le vide) par l'intermédiaire d'un second trou (aire ) (se reporter à la figure (3)).
  4. Indiquer quelle différence fondamentale il existe toutefois entre le système et son analogue électrocinétique.
L'élément bore est omniprésent dans toutes les branches de la chimie. Utilisés en chimie organique comme agents réducteurs, pour des couplages carbone-carbone catalysés par du palladium, les composés du bore sont également importants, entre autres, dans l'industrie du verre (verres borosilicatés), en électronique comme agents dopants, ou encore dans des alliages pour aimants permanents. Nous allons étudier ici quelques bique simple, avec occupation des sommets par des atomes d'aluminium et occupation du milieu de chaque donnés en annexe.

1 Les acides de Lewis dérivés du bore.

Les acides et bases de Lewis sont deux immenses familles de composés, particulièrement utilisés en synthèse organique, en tant qu'activateurs de fonctions ou catalyseurs.
De façon classique, un acide de Lewis est une espèce chimique possédant une lacune électronique, et une base de Lewis est une espèce chimique possédant un doublet non liant. Les acides de Lewis vont facilement réagir avec les bases de Lewis, en s'appropriant leurs électrons.
Un adduit de Lewis est une espèce composée d'un acide et d'une base de Lewis liés entre eux par un doublet liant fourni complètement par la base. Ce type de liaison est appelé liaison covalente de coordination.

1.1 Comparaison de et .

1.1.1 Considérations générales.

  1. Donner le degré d'oxydation du bore et de l'aluminium dans les structures et .
  2. Justifier que et sont bien des acides de Lewis.
  3. Comparer, qualitativement, la force des acides de Lewis et

1.1.2 Pourquoi est un gaz (et un solide) à température ambiante.

La maille élémentaire de la forme du trifluorure d'aluminium peut être décrite comme un réseau cubique simple, avec occupation des sommets par des atomes d'aluminium et occupation du milieu de chaque
arête du cube par un atome de fluor (figure (1)). Les rayons ioniques et atomiques de ces éléments sont donnés en annexe.
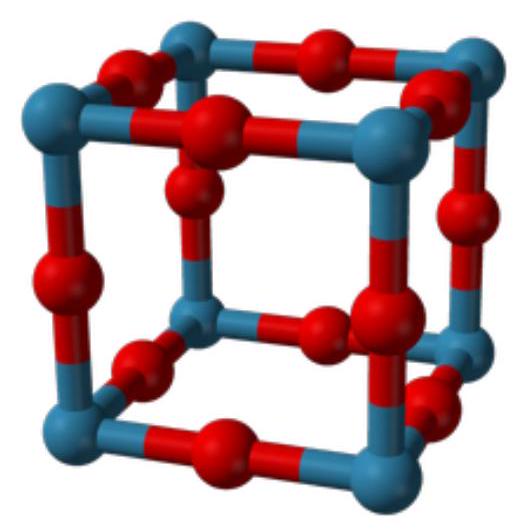
Figure 1 - Structure d'une maille de (bleu : aluminium, rouge : fluor).
  1. Déterminer les coordinences des atomes d'aluminium et de fluor. Préciser la nature des sites occupés.
  2. La masse volumique expérimentale du trifluorure d'aluminium est . En justifiant chaque hypothèse de calcul, et à l'aide des données tabulées, justifier la nature ionique des liaisons fluor-aluminium dans . Commenter. (Une marge d'erreur de sera tolérée dans les résultats numériques.)
Contrairement au trifluorure d'aluminium, dont le point de fusion est d'environ , le trifluorure de bore est un gaz à température ambiante. On admettra que, pour qu'une espèce de type puisse avoir une structure ionique tri-dimensionnelle infinie, l'atome A doit avoir une coordinence de .
6. À l'aide de la charge partielle du bore dans donnée en annexe, calculer le pourcentage d'ionicité de la liaison bore-fluor dans cette structure. En déduire la nature de la liaison bore-fluor, et commenter la valeur expérimentale de donnée en annexe.
7. Déterminer si les données expérimentales sur en annexe sont compatibles avec un réseau cristallin ionique tri-dimensionnel analogue à celui de . Donner, en justifiant, la géométrie avec laquelle elles sont en accord. (Une marge d'erreur de sera tolérée dans les résultats numériques.)
8. Justifier l'appellation de «gaz ionique» pour .

1.2 Étude d'adduits de Lewis.

1.2.1 Approche orbitalaire de la formation d'adduits de Lewis.

  1. Donner la géométrie de la molécule .
Pour déterminer les orbitales moléculaires de , une approche de construction par fragments est adoptée. On considérera d'une part le fragment « », plan, et d'autre part l'atome central de bore.
10. En considérant les 2 sous-fragments « » et « H », représenter l'allure des orbitales du fragment « ». Pour la suite, on considérera que les deux plus hautes orbitales de « » sont dégénérées.
11. Déterminer les orbitales du bore susceptibles d'interagir avec les orbitales du fragment « ». Justifier par considération de symétrie.
12. En déduire les représentations des orbitales moléculaires ( OM ) , et du diagramme orbitalaire de , donné à la figure (2).
13. Identifier l'orbitale la plus haute occupée (HO) et la plus basse vacante (BV) de l'édifice, et préciser le caractère liant, non liant ou antiliant de chacune de ces deux OM.
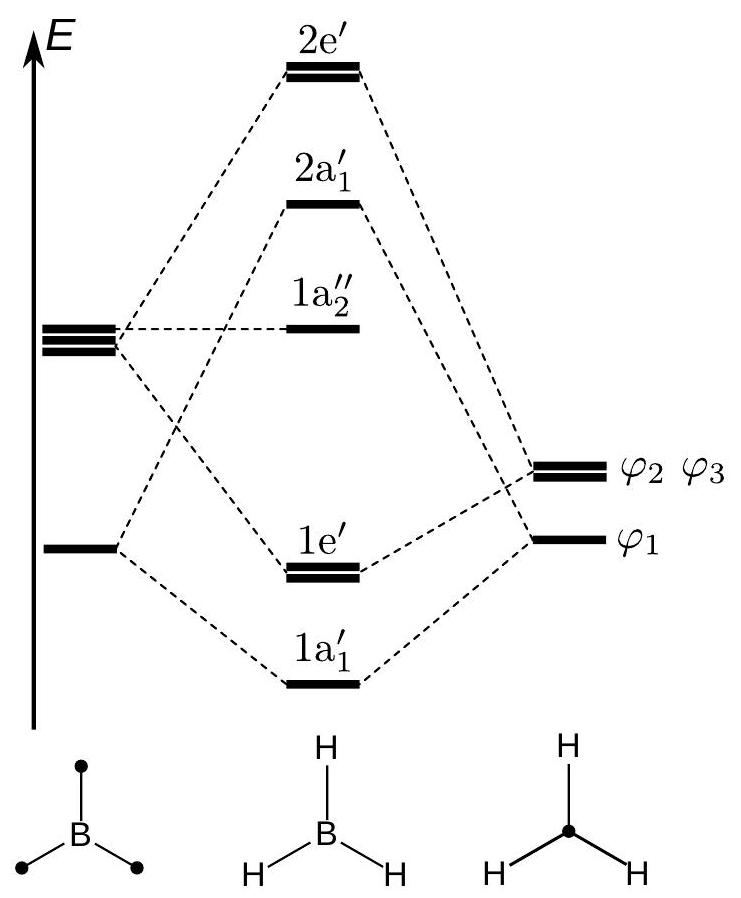
Figure 2 - Diagramme orbitalaire de , par réunion des fragments et B .
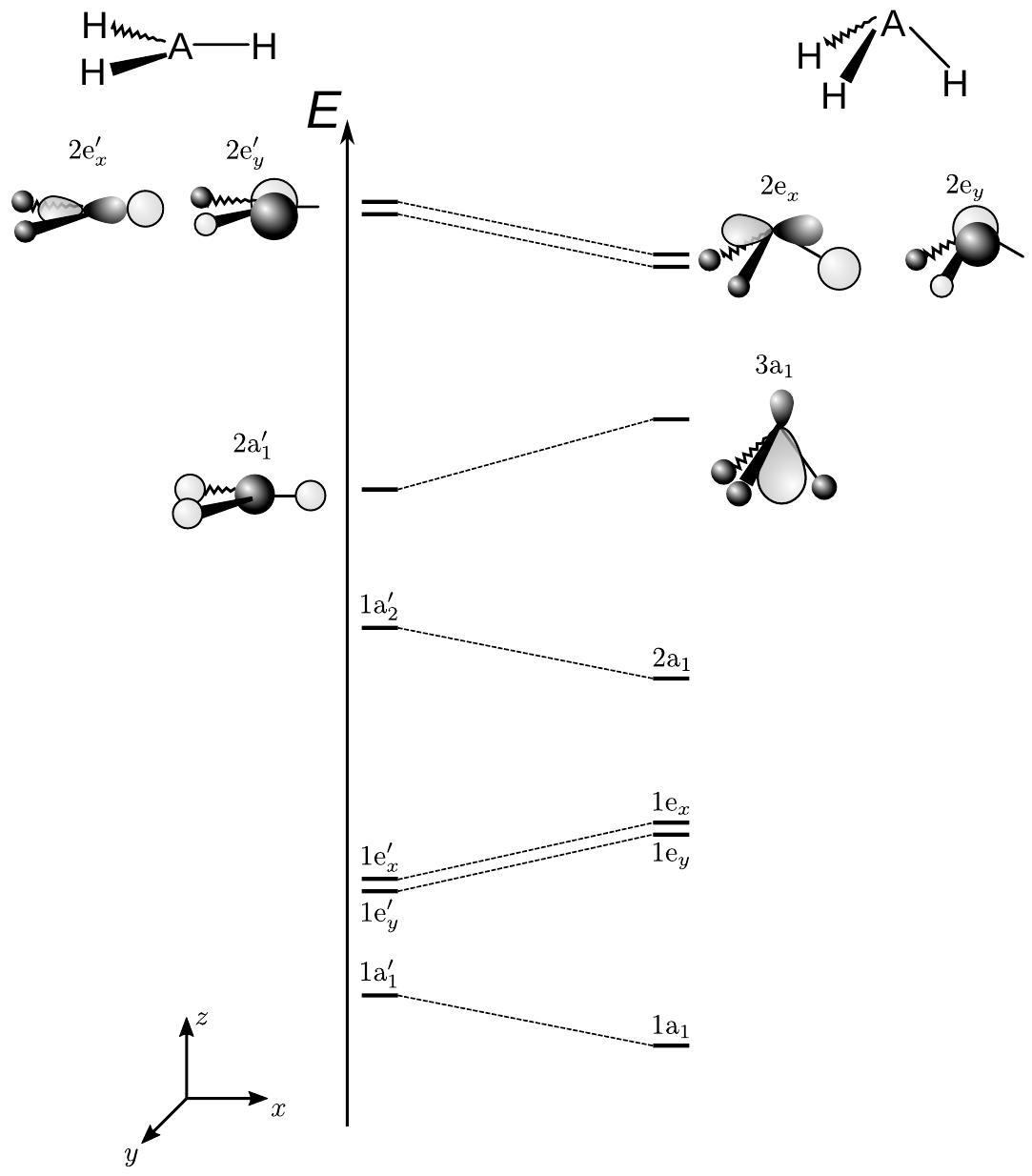
La formation de l'adduit de Lewis s'accompagne de la création d'une liaison bore-azote. Lors de l'approche des deux molécules, se déforme pour adopter une structure pyramide trigonale. L'évolution des orbitales moléculaires est alors décrite par un diagramme de corrélation de Walsch donné figure (3).
Figure 3 - Diagramme de corrélation de Walsch d'une molécule , de la géométrie trigonale plane (à gauche) à une géométrie pyramidale à base triangulaire (à droite).
  1. Proposer l'allure des orbitales et , en s'inspirant des OM représentées sur la figure (3).
  2. Justifier la stabilisation de l'OM lors du changement de géométrie de .
  3. Préciser en justifiant la(les) différence(s) attendue(s) entre les diagrammes de et de .
  4. Déterminer les orbitales de et de qui interagissent pour former la nouvelle liaison. Justifier.
  5. Justifier l'utilisation du terme «liaison covalente de coordination » pour décrire l'interaction bore-azote dans cet adduit.

1.2.2 Paire de Lewis frustrée.

Dans le cas où l'acide de Lewis et la base de Lewis sont très encombrés, aucune liaison ne peut se former. On appelle alors le mélange stœchiométrique d'un tel acide et d'une telle base une « paire de Lewis frustrée ». Un exemple classique est constitué de trimésitylphosphine 1, noté (Mes = groupement Mésityl -triméthylphényl) et de tri(pentafluorophényl)bore de formule .
19. Représenter le produit 1 et justifier qu'il s'agit bien d'une base de Lewis.
20. Représenter le produit 2. Expliquer l'intérêt d'utiliser des substituants fluorés ici.
21. Comparer les niveaux énergétiques de la HO et de la BV d'une paire de Lewis dans le cas où elle formerait une paire frustrée avec le cas où elle forme un adduit de Lewis, et justifier la réactivité de la paire frustrée.
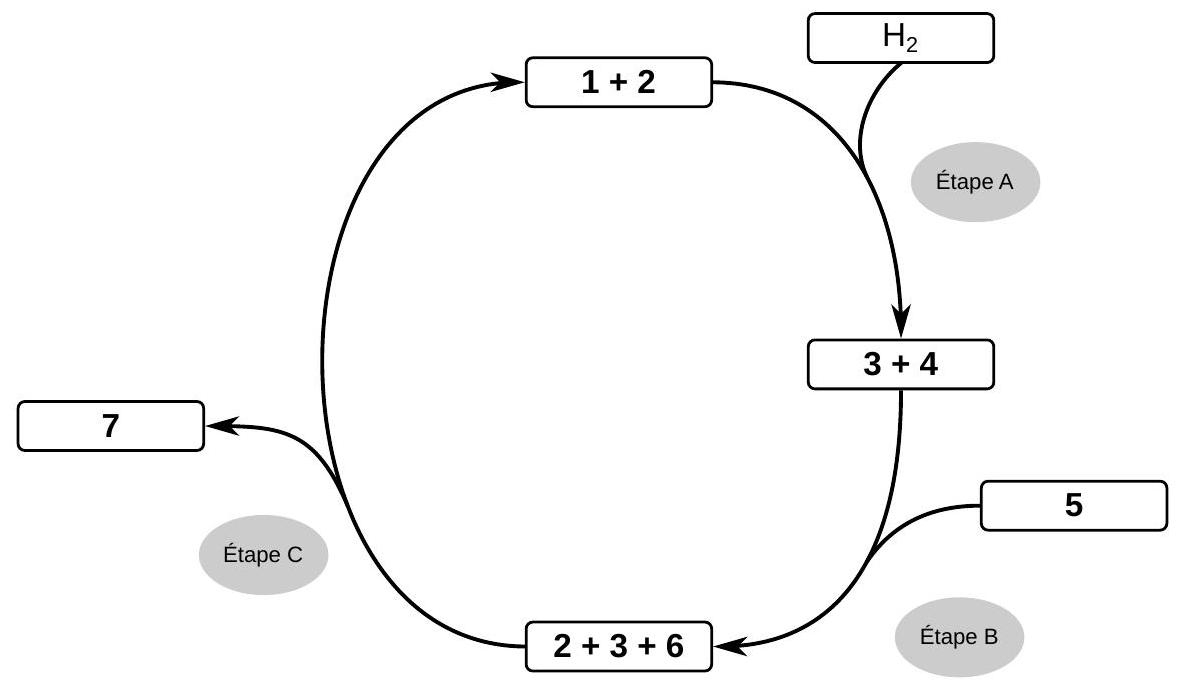
Sous atmosphère inerte, on fait buller du dihydrogène pendant 30 minutes dans un mélange équimolaire de 1 et dans le toluène ( 20 mL ). La solution est ensuite agitée pendant 12 h à température ambiante, sous atmosphère de dihydrogène. Le toluène est ensuite partiellement évaporé à l'aide d'un évaporateur rotatif, et 10 mL d'hexane sont ajoutés. Un précipité blanc apparaît, et est filtré, puis lavé avec de l'hexane froid, puis séché sous vide. Ce solide blanc est ensuite dissout dans du bromobenzène deutéré pour mener des analyses en RMN du proton , du bore (spin du noyau : ) et du phosphore (spin du noyau: ).
Figure 4 - Cycle catalytique de la réaction.
Le spectre RMN du proton de ce solide ionique est donné tableau (1). Le spectre RMN du bore ne présente qu'un seul signal large à . Le spectre RMN du phosphore ne présente qu'un seul signal sous forme d'un doublet ( ). On donne également en annexe le spectre RMN du bore du mélange équimolaire de et , réalisé dans le chloroforme deutéré en présence de (figure (7)).
Déplacement chimique (ppm) Multiplicité Intégration
7,91 doublet ( ) 1 H
6,58 doublet ( ) 6 H
4,10 quadruplet ( ) 1 H
1,95 singulet 9 H
1,87 singulet 9 H
1,62 singulet 9 H
Tableau 1 - Tableau des déplacements chimiques du spectre du solide blanc .
22. Expliquer l'intérêt d'utiliser un solvant deutéré en RMN du proton, et donner la raison de l'ajout de .
23. Vérifier en justifiant si le spectre RMN du mélange avant réaction est compatible avec la présence d'une paire de Lewis frustrée.
24. À l'aide des spectres obtenus après réaction et de la table de déplacement chimique en annexe (figure (8)), déterminer les structures des composés et qui composent le solide blanc obtenu.
25. Attribuer les différents signaux en (tableau (1)) et commenter la multiplicité du signal à 4,10 ppm.
Le mélange équimolaire a été utilisé comme catalyseur pour l'hydrogénation catalytique du 1,1diphényléthène : on dissout et le mélange ( 0,01 équivalent) dans du toluène à température ambiante, et on fait buller du dihydrogène à pression atmosphérique. La disparition de et l'apparition de 7 sont suivies par spectrométrie de masse. En 15 minutes, la conversion est complète.
26. Donner la structure du composé 5. Il est synthétisé à partir de diphénylméthanone et de méthylènetriphénylphosphorane. Proposer l'équation-bilan de la réaction de la formation de , et préciser quelle est la force motrice de cette réaction.
27. Donner la structure de l'intermédiaire 6 et du produit final 7 du cycle catalytique de la figure (4). Attribuer le nom des étapes A, B et C parmi « Transfert de proton», «Coupure hétérolytique» et « Transfert d'hydrure ».
28. Donner deux avantages de ce procédé par rapport à d'autres permettant les mêmes types de réaction.

1.3 Un catalyseur au bore particulier : l'oxazaborrolidine CBS.

Dans les années 1980, l'essor de la synthèse asymétrique a donné lieu à d'intenses recherches de cata- lyseurs chiraux permettant de rendre stéréosélective un grand nombre de réactions. Les chimistes Corey, Bakshi et Shibata ont ainsi développé un composé du bore particulier, appelé désormais selon leurs initiales, l'oxazaborrolidine CBS 8. 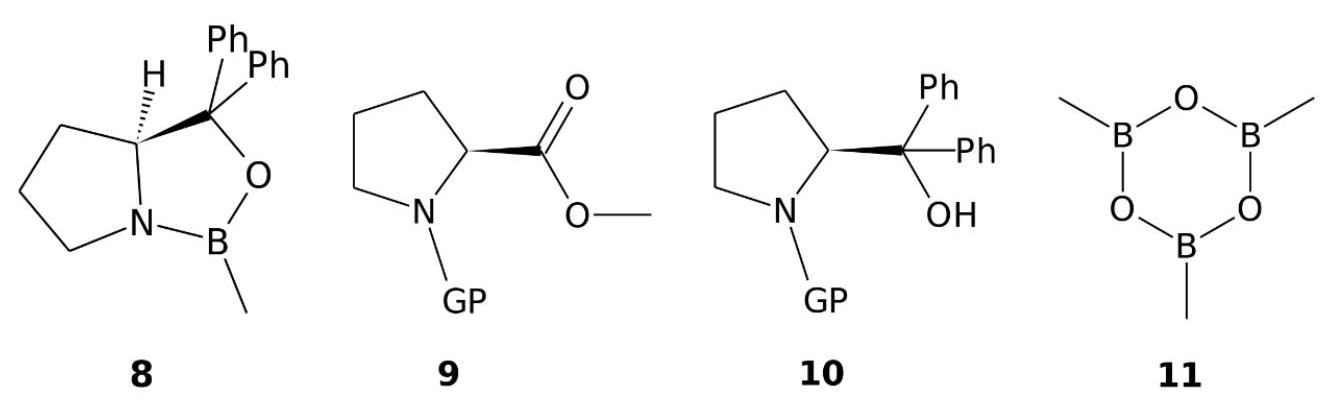L'oxazaborrolidine CBS est synthétisée à partir de l'ester méthylique de la proline protégée (on note GP le groupe protecteur de la fonction amine).
Figure 5 - Structure des produits 8, 9, 10 et 11.
  1. Rappeler la classe de molécules naturelles dont fait partie la proline.
  2. Proposer une courte voie de synthèse de l'alcool groupement phényle à partir de . On supposera que le groupe protecteur «GP» résiste aux conditions expérimentales de cette synthèse.
Le dérivé 10 est déprotégé, puis est mis à réagir avec du tri-méthyl boroxime 11, (figure (5)), avec du toluène, dans un montage de type Dean-Stark, pour donner l'oxazaborrolidine CBS 8.
31. Faire un schéma d'un montage Dean-Stark et justifier l'intérêt d'utiliser un montage Dean-Stark dans le cas de cette réaction.
Une version protonnée 12 du CBS est utilisée comme catalyseur chiral de la réaction de Diels-Alder entre le cyclohexa-1-3-diène 13 et la méthylacroléine 14 dont la structure est donnée à la figure (6). L'énantiomère majoritaire 15-S a une configuration absolue « S ».
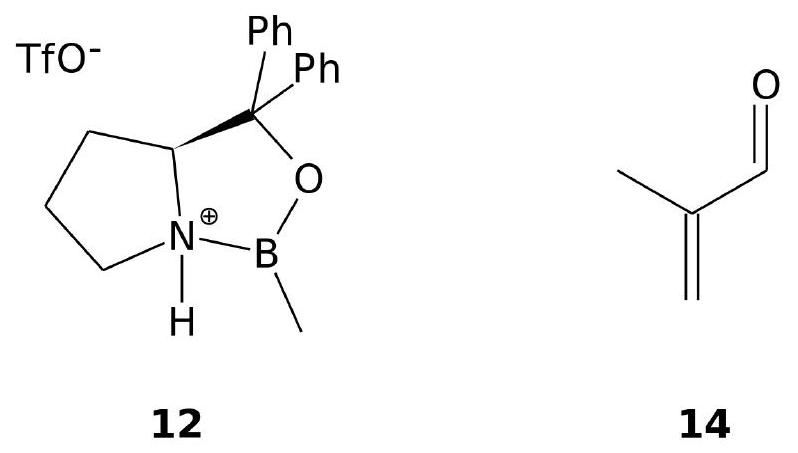
Figure 6 - Structure des produits 12 et 14.
  1. Donner les produits majoritaires 15 de la réaction de Diels Alder entre ces deux réactifs en l'absence de CBS. Justifier leur stéréochimie à l'aide d'une représentation de l'approche des deux réactifs.
  2. Proposer une structure pour l'adduit de Lewis qui se forme entre la methylacroléine et le CBS protonné.
  3. Donner une explication sur le caractère énantiosélectif de la réaction et représenter l'énantiomère majoritaire 15-S (on ne cherchera pas à justifier l'obtention de cet énantiomère plutôt que l'autre).
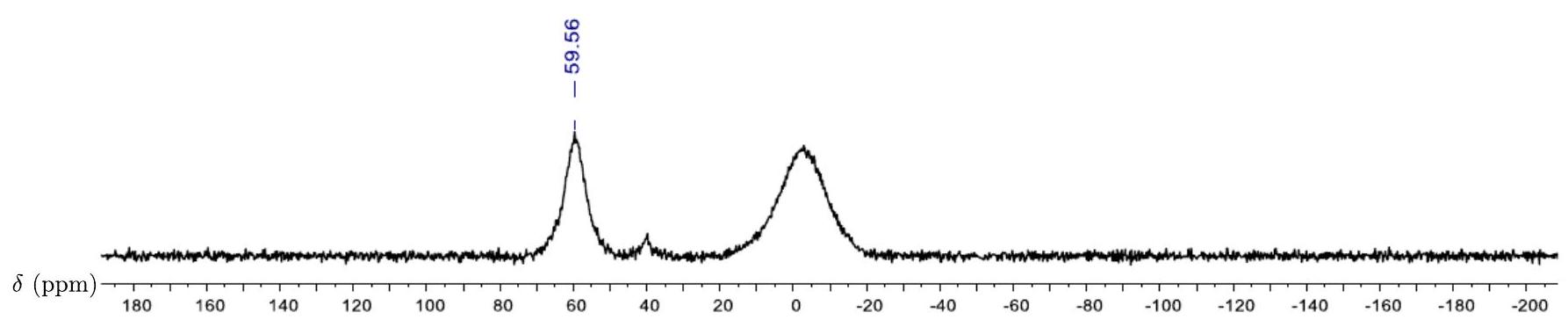
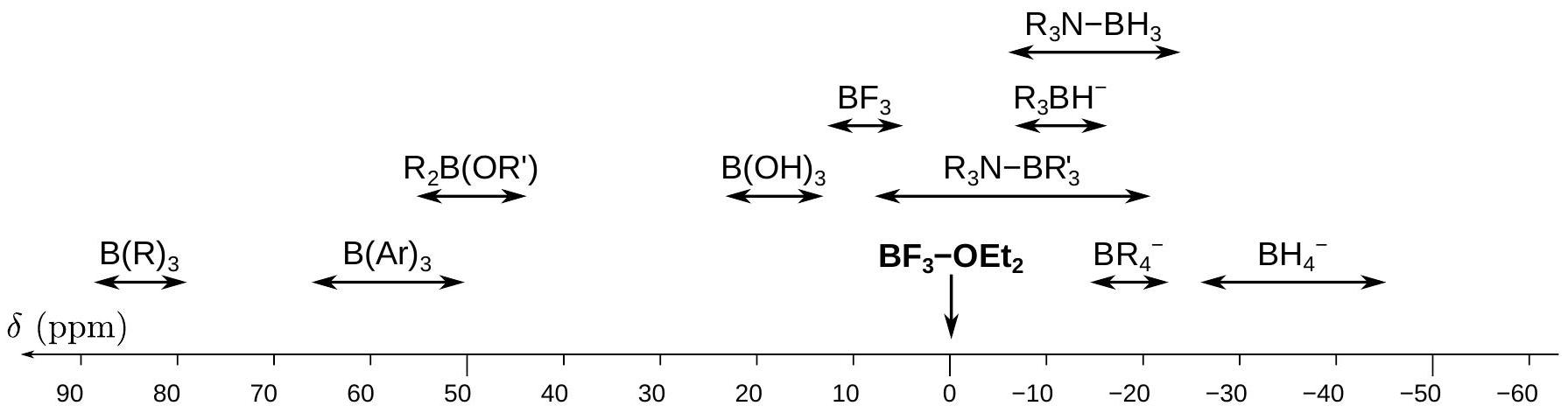
Figure 7 - Spectre RMN ( 160 MHz ) du composé 2 en présence de . Solvant : chloroforme deutéré.
Figure 8 - Table des déplacements chimiques en RMN du bore .
Figure 8 - Table des déplacements chimiques en RMN du bore .
  • Spin nucléaire du :
  • Énergie de liaison

2 Annexes.

2.1 Données.

  • Nombre d'Avogadro :
  • Caractéristiques de :
    Charge partielle
Bore Aluminium Fluor
Numéro atomique 5 13 9
Masse molaire atomique 10,8 27,0 19,0
Rayons ioniques
Rayons atomiques
  • Spin nucléaire du
  • Énergie de liaison

\subsection*{2.2 Figures et tables complémentaires.

2 Figures et tables complémentaires.}

    1. Il s'agit de nombres "moyens", c'est-à-dire non sujets aux fluctuations temporelles d'origine microscopique. Le temps caractéristique de ces dernières est très inférieur à celui de l'évolution de ces nombres et à laquelle nous allons nous intéresser.
    1. Il s'agit, en réalité, de la section "efficace" de diffusion, ou de collision.
ENS Physique Chimie L PC 2023 - Version Web LaTeX | WikiPrépa | WikiPrépa