compris les calculatrices programmables et alphanumériques ou à écran graphique, à condition que leur fonctionnement soit autonome et qu'il ne soit pas fait usage d'imprimante. Une seule calculatrice à la fois est admise sur la table et aucun échange n'est autorisé entre les candidats.

Sur la modélisation de certains phénomènes atmosphériques

Cette épreuve traite de divers processus physiques liés à l'atmosphère et sa dynamique. Elle est constituée de quatre parties largement indépendantes. Dans la partie I, on examine quelques contraintes expérimentales associées à la mesure de la taille des gouttelettes d'eau formant les nuages par un dispositif de télédétection. La partie II étudie les conditions optiques de formation de certains mirages. Dans la partie III, après avoir étudié la stabilité générale de l'atmosphère terrestre, on détermine les conditions thermodynamiques d'obtention des mirages. Finalement, dans la partie IV, on s'intéresse à la formation des nuages dans l'atmosphère terrestre.

Données numériques et ordres de grandeur :

Viscosité dynamique de l'air

Diffusivité thermique de l'air

Masse molaire moyenne de l'air

Enthalpie massique de vaporisation de l'eau

Capacité thermique massique de la vapeur d'eau

Pression de vapeur saturante de l'eau à la température

Coefficient de tension superficielle de l'eau

Masse molaire de l'eau

Température moyenne au sol

Pression moyenne au sol

Constante des gaz parfaits

Constante de Planck

1 Mesure LIDAR de la taille des gouttelettes d'un nuage

Un LIDAR (acronyme anglais pour LIght Detection And Ranging) est un système de mesure dont le fonctionnement est semblable à celui du radar mais dont le domaine spectral est différent : alors que le radar fonctionne dans le domaine des ondes radio, le LIDAR couvre le domaine du visible et de l'infrarouge. Un LIDAR se compose d'un système laser chargé d'émettre des ondes lumineuses vers l'atmosphère depuis le sol. Ces ondes interagissent avec les différents composants qu'elles rencontrent (gouttelettes d'eau, poussières, cristaux de glaces et aérosols) et sont diffusées dans pratiquement toutes les directions. Les photons ayant été diffusés vers l'arrière retournent vers un télescope situé au sol et généralement couplé à la station d'émission. On peut alors déduire des informations sur le diffuseur comme sa concentration, la taille des particules ou sa distance par rapport au système de mesure. On suppose que le laser utilisé émet une lumière dont la longueur d'onde est de 532 nm .

A votre avis, quel est la couleur du laser?
Evaluer l'intervalle de temps entre l'émission d'une impulsion laser et la réception du premier signal de retour par le télescope en utilisant un ordre de grandeur raisonnable de l'altitude minimale de formation des nuages.
Le signal reçu par le télescope est couplé à un système de comptage des photons par photomultiplicateur dont la carte d'acquisition possède une fréquence d'échantillonnage de 10 MHz et ne peut acquérir plus de 2000 points. Donner l'altitude maximale d'observation des nuages ainsi que l'incertitude sur l'estimation de la distance des gouttelettes.
L'énergie lumineuse par impulsion est d'environ 150 mJ et la durée d'une impulsion est de l'ordre de 5 ns . Calculer la puissance lumineuse d'une impulsion et estimer le nombre de photons émis à chaque impulsion.
Quelle relation doit exister entre la longueur d'onde et le rayon des gouttelettes pour que les rayons lumineux suivent les lois de l'optique géométrique à l'interface avec la gouttelette et à l'intérieur?
Dans cette hypothèse, on admet que très peu de photons sont renvoyés vers le télescope. En déduire un ordre de grandeur de la taille maximale des gouttelettes d'eau qui pourront être observées par LIDAR.

2 Observation de mirages inférieurs et supérieurs.

L'observation de mirages dits inférieurs se produit généralement en été lorsque la température de l'air augmente notablement au contact d'un sol chauffé par le soleil. La masse volumique de l'air et l'indice de réfraction de l'air augmentent alors avec l'altitude. On étudie, dans cette partie, la propagation de rayons lumineux dans un tel milieu stratifié horizontalement.

On considère un individu recevant des rayons lumineux d'un objet vertical situé à une distance horizontale

devant lui. Pour repérer la marche des rayons, on utilise un repère

dont l'origine

est situé au sol, au pied de l'observateur. La variable

est l'altitude depuis le sol et

repère la position horizontale. Les coordonnées des yeux de l'observateur sont alors (

) où

(voir la figure 1 ). En un point d'un rayon lumineux, on appelle

, l'angle entre l'axe vertical et la tangente au rayon lumineux orientée dans le sens de la propagation,

désignant la valeur de cet angle au niveau de l'observateur (

On admet que le profil d'indice près du sol peut être modélisé par une fonction de la forme avec . Donner l'unité et le signe de puis tracer l'allure de la courbe .
Sous cette hypothèse, on peut montrer que les rayons lumineux entre un point de l'objet d'altitude et l'oeil de l'observateur suivent une parabole de la forme :

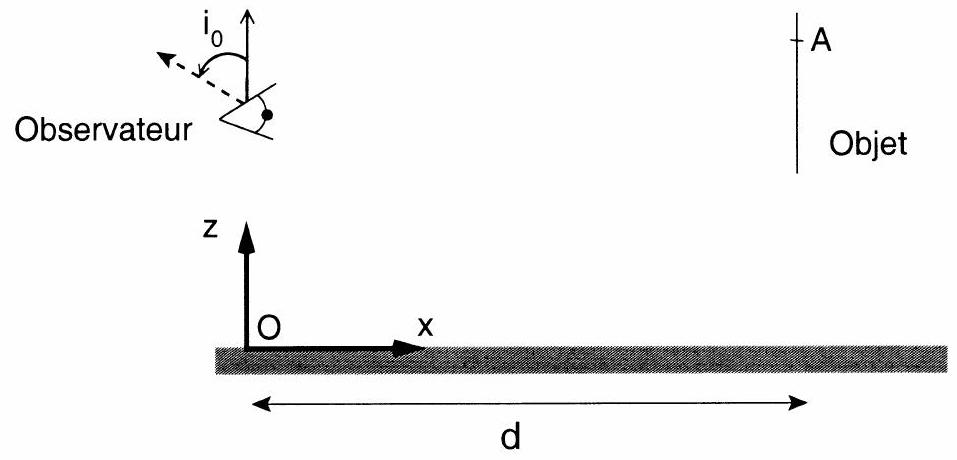
Fig. 1 - Schéma et notations utilisés pour l'observation d'un mirage optique

Montrer qu'il existe deux valeurs possibles de

, et donc deux paraboles distinctes, si la différence d'altitude

entre le point A et l'observateur vérifie la condition

Dans cette question, on pourra poser

.
3. Montrer qu'une augmentation de l'altitude du point

conduit à une augmentation de l'angle

au niveau de l'observateur si une nouvelle condition que l'on exprimera en fonction de

est vérifiée.
4. Démontrer que l'une des paraboles la vérifie et l'autre non.
5. En déduire que l'observateur peut voir deux images d'un objet dont les coordonnées vérifient l'équation (2), l'une droite et l'autre renversée. On pourra illustrer cette propriété par un schéma. Laquelle de ces images correspond à ce qu'on appelle traditionnellement un mirage optique ou mirage inférieur?
6. Le 26 Avril 1977, les habitants de Grand Haven dans le Michigan, regardant dans la nuit par dessus les eaux froides du Lac Michigan ont observé distinctement dans le ciel, les lumières du phare de Milwaukee situé pourtant à plus de 120 kilomètres. Expliquer brièvement ce phénomène.

3 Stabilité de l'atmosphère; convection

Dans cette partie, on étudie certaines propriétés de stabilité de l'atmosphère terrestre que l'on considère constituée d'air sec se comportant comme un gaz parfait. On rappelle que pour un gaz diatomique, les capacités thermiques molaires à volume et pression constants valent respectivement

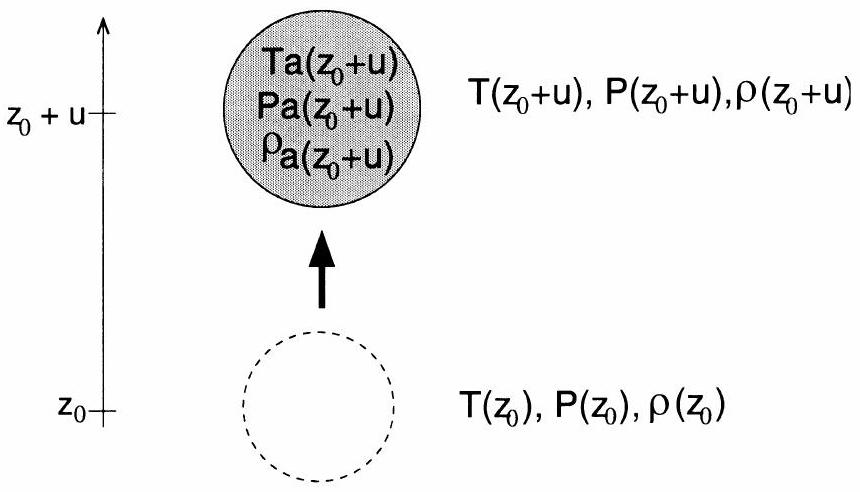
. Les valeurs massiques seront notées

. En outre, on néglige les variations de la gravité avec l'altitude. Les autres variables sont des fonctions de l'altitude

Fig. 2 - Déplacement vertical élémentaire d'une parcelle d'air.

Stabilité d'une atmosphère

On considère tout d'abord un modèle d'atmosphère isotherme en équilibre hydrostatique avec le champ de pesanteur. Donner l'expression de la pression en fonction de et des grandeurs au sol. Ce modèle est-il, à votre connaissance, réaliste?

Pour étudier la stabilité d'une atmosphère, on cherche à déterminer l'effet d'une fluctuation atmosphérique quelconque sur une parcelle d'air. On considère une parcelle d'air de masse

constante et de volume

variable initialement en équilibre à l'altitude

et déplacée verticalement jusqu'à l'altitude

avant de laisser

évoluer librement avec le temps. On supposera que

. Les valeurs de la densité

, de la température

, de la pression

de la parcelle à l'altitude

sont a priori différentes des mêmes grandeurs

de l'air environnant à l'équilibre thermodynamique (voir la figure 2). On suppose que le temps de mise à l'équilibre mécanique local entre la parcelle d'air et l'atmosphère environnante est très rapide contrairement à l'équilibre thermique.
2. Quelle est la relation entre les pressions

?
3. Montrer que pour des variations élémentaires de température

et de pression

, la chaleur échangée par la parcelle d'air avec son environnement est

On suppose que le déplacement de la parcelle est suffisament rapide pour que cette transformation soit adiabatique. Montrer alors que le gradient de température de l'air situé dans la parcelle suit la relation

Ce gradient est généralement appelé gradient adiabatique sec. Calculer sa valeur en

puis en K.

.
5. Effectuer le bilan des forces sur la parcelle d'air à l'altitude

et l'exprimer en fonction de

.
6. Démontrer au premier ordre en

que

En déduire l'équation différentielle qui régit le déplacement de la parcelle autour de l'altitude en fonction du temps. On fera apparaître la grandeur caractéristique définie localement par

et dont on précisera l'unité.
8. Donner les solutions du mouvement de la parcelle d'air suivant la valeur du gradient de température local en

. En déduire un critère d'instabilité de la parcelle d'air.
9. Les dix premiers kilomètres de l'atmosphère forment la troposphère et les observations montrent que le gradient vertical de température peut être considéré comme constant et de l'ordre de

. Discuter la stabilité générale de la troposphère et indiquer comment varie

dans la troposphère.
10. Calculer la période d'oscillation (appelée période de Brunt-Väisälä) d'une parcelle d'air à la base et au sommet de la troposphère.

Application à la formation des mirages optiques

On cherche à préciser les conditions dans lesquelles peuvent se former les mirages optiques inférieurs étudiés dans la partie 2.
11. A l'aide d'une analyse dimensionnelle, estimer le temps nécessaire à la conduction thermique pour que le profil de température entre une fine couche d'air chaud située près du sol et une couche d'air moins chaud située par exemple à 1 mètre au-dessus atteigne l'état stationnaire. Commenter ce résultat.
12. Il n'est pas rare d'observer en été des différences de température de l'ordre de

entre un sol fortement chauffé et les couches supérieures proches. En utilisant les résultats de la partie précédente, prévoir qualitativement le mouvement d'une telle couche d'air chaud.
13. On admet que l'indice optique

de l'air suit la loi de Gladstone telle que

où

est une constante dimensionnée et

la masse volumique de l'air. En utilisant la partie 2 , montrer qu'un mirage inférieur ne peut se former que si le gradient vertical de température vérifie la condition

Déduire des résultats précédents que l'observation d'un mirage n'est pas compatible avec une atmosphère en équilibre stable.

4 Formation des nuages

Bien que la vapeur d'eau soit un constituant minoritaire de l'atmosphère, elle joue un rôle fondamental dans de nombreux processus climatiques comme les précipitations neigeuses ou la pluie. On se propose dans cette partie d'étudier la formation des nuages et on considère à présent l'air comme un mélange d'air sec et de vapeur d'eau, se comportant tous les deux comme des gaz parfaits.

Questions préliminaires : Propriétés d'un air humide

La masse de vapeur d'eau présente par kilogramme d'air sec est appelée rapport de mélange et sera notée . Exprimer la capacité thermique massique d'un air humide à pression constante en fonction de et où est la capacité thermique massique de la vapeur d'eau à pression constante.
Au sol et pour un air saturé en vapeur d'eau, le rapport de mélange est de l'ordre de . Justifier que, dans ces conditions, il est raisonnable de prendre la capacité thermique massique d'un air humide à pression constante égale à celle d'un air sec en calculant l'erreur relative engendrée sur la valeur de la capacité thermique massique.

Questions préliminaires : Equilibre liquide-vapeur

On considère le changement d'état entre la vapeur d'eau et l'eau liquide au sein de l'atmosphère.
3. Justifier que l'enthalpie libre

est la fonction d'état la plus pertinente pour décrire l'évolution et l'équilibre de l'eau entre les deux phases.
4. A l'équilibre thermodynamique, quelle est la relation entre les potentiels chimiques standards de référence de l'eau

(respectivement pour les phases liquide et vapeur), la pression de vapeur saturante

et la pression de référence

prise égale à 1 bar.
5. A partir de l'équation de Clapeyron, retrouver l'équation donnant

en fonction de

. On considérera que l'enthalpie massique de vaporisation de l'eau est indépendante de la température.

Hauteur de formation des nuages

Pour étudier certaines propriétés des nuages, on fait l'hypothèse que les échanges thermodynamiques entre les différentes parcelles d'air de l'atmosphère sont adiabatiques conformément à la question 3.4. On ne tiendra donc pas compte du profil réel de température évoqué à la question 3.9.
6. Donner le profil de température

de l'air en fonction de l'altitude.
7. Déterminer le profil de pression

. On pourra introduire le facteur

La sensation d'un individu de se trouver dans un air plus ou moins humide est liée à l'humidité relative ou degré hygrométrique

défini par

où

est la
pression partielle de vapeur d'eau et

la pression de vapeur saturante de l'eau à la température

locale de l'air humide.
8. On considère que la pression partielle de vapeur d'eau est proportionnelle à la pression de l'air. En prenant un degré d'humidité au sol

, donner la loi

.
9. Montrer que pour des altitudes inférieures à dix kilomètres,

peut être approximée par une fonction affine.
10. A partir de la condition de saturation de l'atmosphère, estimer avec la méthode de votre choix, la hauteur à laquelle se forment des nuages.
11. En déduire la température de formation des nuages ainsi que la pression partielle de vapeur d'eau correspondante.
12. Un tel équilibre liquide-vapeur est-il thermodynamiquement possible dans ces conditions? En déduire une information supplémentaire sur la composition probable des nuages.

Croissance et formation des gouttelettes d'eau

Les observations montrent que l'apparition de gouttelettes d'eau en suspension ne se fait que pour des humidités relatives supérieures à

. On parle alors d'air supersaturé. Une des raisons est que la formation de ces gouttes approximativement sphériques nécessite une énergie supplémentaire appelée tension superficielle correspondant à l'énergie de formation d'une interface entre la phase liquide et la phase vapeur. La surface de cette interface est donc égale à la surface de la goutte.
On considère le système constitué de

moles de vapeur d'eau entourant une gouttelette d'eau sphérique de rayon

et contenant

moles d'eau. Le nombre total de moles d'eau

est supposé constant ainsi que la température

et la pression totale imposées par l'air environnant. On suppose aussi que la pression partielle de l'eau dans la phase liquide

est égale à celle de la vapeur d'eau

.
Pour tenir compte de la tension superficielle, il faut rajouter à la fonction d'état

, l'énergie supplémentaire

où

est la surface de la goutte et

le coefficient de tension superficielle.
13. Avant l'apparition d'une gouttelette d'eau, on suppose que toute l'eau est sous forme de vapeur à la pression partielle

. Quelle est l'expression de l'enthalpie libre initiale

en fonction de

où

est le potentiel chimique de l'eau dans la phase vapeur, puis de

?
14. Lorsqu'une gouttelette s'est formée, donner l'expression de l'enthalpie libre

du système en fonction de

où

est le potentiel chimique de l'eau dans la phase liquide.
15. A l'aide de la question 4.4 , montrer que la fonction

peut s'écrire comme un polynôme en

de la forme

où

sont des coefficients que l'on déterminera en fonction de

la masse volumique de l'eau,

.
16. A partir du tracé de

, montrer que seules les gouttelettes ayant un rayon initial supérieur à une valeur critique

, dont on donnera l'expression, peuvent croître spontanément.
17. Tracer qualitativement la fonction

. Estimer la valeur du rayon critique pour une humidité relative caractéristique

.
18. A votre avis, quel rôle jouent les poussières atmosphériques dont la taille est de l'ordre du micromètre dans la formation des nuages?

Stabilité des nuages

Sous l'effet de la gravité, les gouttelettes formées peuvent chuter vers le sol. Estimer la vitesse limite de chute des gouttelettes de rayons 10 et . On vérifiera et discutera la validité des lois utilisées.
En déduire leur temps caractéristique de descente jusqu'au sol. Commenter les résultats.
La taille moyenne des gouttelettes d'eau formant un nuage est de . Pourquoi ne voit-on pas les nuages tomber?