J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Mathématiques 2 MP 2008

Support de la transformation de Radon

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Fonctions (limites, continuité, dérivabilité, intégration)Calcul différentiel et fonctions à plusieurs variablesIntégrales à paramètresGéométrieIntégrales généralisées
Logo mines
🔗 Explorer
Banque
Mines
Année
2008
Filière
MP
Matière
Maths
Mines MPMines 2008MP MathsMaths 2008
2025_08_29_dacc50441e808f6f9032g

ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES.

ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE. ÉCOLE POLYTECHNIQUE (Filière TSI).
CONCOURS D'ADMISSION 2008

SECONDE ÉPREUVE DE MATHÉMATIQUES

Filière MP

(Durée de l'épreuve : 4 heures) L'usage d'ordinateur ou de calculette est interdit.
Sujet mis à la disposition des concours : ENSAE ParisTech, ENSTIM, TELECOM SudParis (ex TELECOM INT), TPE-EIVP, Cycle international
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
MATHÉMATIQUES II - MP
L'énoncé de cette épreuve comporte 7 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Support de la transformation de Radon

Notations de géométrie

Dans tout le problème, on se place dans le plan affine , muni d'un repère orthonormé direct et de la norme euclidienne, notée . On notera ( ) les coordonnées dans ce repère d'un élément . L'application permettra d'identifier le plan affine et l'espace vectoriel . On introduit les notations suivantes:
Soit , on note
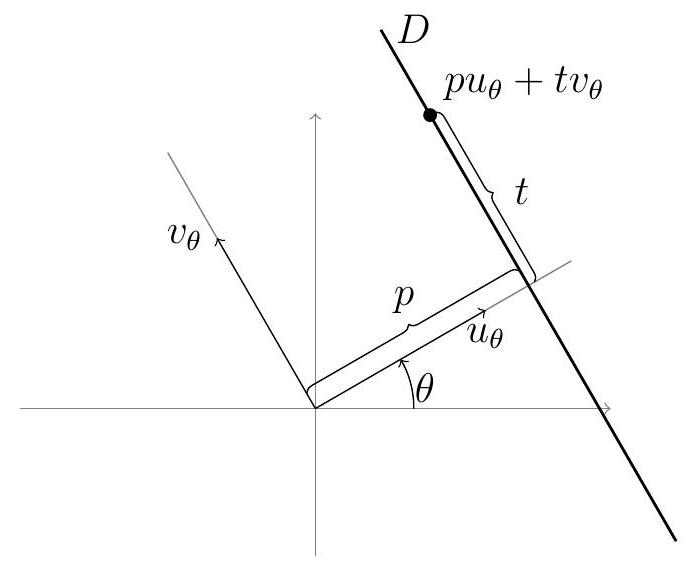
Pour tout , on note la rotation de centre 0 et d'angle . Ainsi,
Fig. 1 - Notations
À toute droite affine ne passant pas par l'origine, on associe un unique couple ( ) où et sont tels que
Si passe par l'origine, on lui associera l'unique couple ( ) qui convienne avec . On appelle et les paramètres de la droite .

Notations d'analyse

Pour ou et fonction de dans , on appelle support de , noté , l'adhérence de l'ensemble des points où est non nulle. Pour ou , on note l'ensemble des fonctions de dans , de classe sur , à support compact : il existe , dépendant de , avec si , où si . En d'autres termes, supp si et supp si . On notera que de telles fonctions sont bornées et on posera
Pour les fonctions de dans , si , on utilisera, selon le contexte, la notation ou la notation pour représenter l'image de par .
Pour , il existe tel que supp et alors
è
On note la valeur commune de toutes les intégrales sur un intervalle contenant le support de .
Le même principe vaut pour la dimension 2 : pour , on remarque que
pour tout compact qui contient où est tel que supp . On note
Définition 1. On dit qu'une fonction est radiale lorsque pour tout .
Pour , continue, nulle en dehors d'un intervalle , on pose
On admet que est continue, nulle en dehors de et que est dérivable avec

I Un peu de géométrie

  1. Soit . Montrer que si est radiale, il existe telle que
  1. Soit ; pour , on considère la fonction
Montrer que la fonction est continue sur et que pour tout , la fonction est -périodique.
3. Montrer que la fonction
est radiale.
4. Soit , que l'on écrit où appartient à . Soit et . Montrer que l'ensemble
est une droite dont on précisera les paramètres en fonction de et . On pourra commencer par étudier .

II Lemme préparatoire

Soit , on note l'ensemble
L'objectif de cette partie est de montrer le lemme suivant.
Lemme 1. Soit telle que pour tout ,
alors est nulle sur le complémentaire de .
Fig.
  1. Soit . Soit . Montrer que les applications
sont dérivables sur et calculer leur dérivée.
6. Soient et deux éléments de et soit . En utilisant la formule de Green-Riemann, montrer l'identité :
Dans les questions 7 à 13, on suppose que vérifie les hypothèses du lemme.
7. Établir, pour tout , les deux identités suivantes:
  1. Soit . Montrer que et sont constantes sur et établir, pour tout , les relations :
et
Pour , on introduit les fonctions suivantes:
Plus généralement, pour une fonction de dans , on note la fonction définie par
  1. Montrer que et satisfont les hypothèses du lemme.
  2. Soit . Montrer, pour tous les entiers et , l'identité suivante :
On pourra raisonner par récurrence sur .
11. Soit . En déduire, pour tout entier , les identités :
  1. Établir, pour tout , que
  1. Prouver le lemme.

III Théorème de support

Définition 2. Pour , on pose
On veut montrer le théorème de support suivant :
Théorème 1. Soit . Si il existe tel que pour quel que soit alors pour .
Soit une fonction qui satisfait les hypothèses du théorème. On suppose dans les questions 14 à 16 que est radiale. Soit telle que .
14. Montrer, pour tout et pour tout , les identités suivantes :
  1. Établir, pour tout , l'identité
  1. En déduire que est nulle sur .
On ne suppose plus que est radiale. Soit un élément quelconque de .
17. Établir, pour tout , l'identité
  1. Montrer pour tout , la propriété :
  1. Quel est géométriquement, l'ensemble ? Que signifie géométriquement la condition ?
  2. Prouver le théorème.
    FIN DU PROBLÈME
Mines Mathématiques 2 MP 2008 - Version Web LaTeX | WikiPrépa | WikiPrépa