Version interactive avec LaTeX compilé

Mines Option Informatique MP 2013

Recherche de motif dans un texte

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

Mines MP Mines 2013 MP Info Info 2013

2025_08_29_0dd0fda955395b3aa143g

A 2013 INFO. MP
ECOLE DES PONTS PARISTECH, SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH, MINES DE SAINT-ETIENNE, MINES DE NANCY, TELECOM BRETAGNE, ENSAE PARISTECH (FILIERE MP) ECOLE POLYTECHNIQUE (FILIERE TSI)

CONCOURS 2013
EPREUVE d'INFORMATIQUE
Filière : MP
Durée de l'épreuve : 3 heures. L'utilisation d'une calculatrice est autorisée.

Sujet mis à la disposition des concours : Cycle International, ecoles des Mines, TELECOM SudParis, TPE-EIVP.

L'énoncé de cette épreuve comporte 14 pages.

Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :

INFORMATIQUE - MP

Recommandations aux candidats

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Tout résultat fourni dans l'énoncé peut être utilisé pour les questions ultérieures même s’il n’a pas été démontré.
Il ne faut pas hésiter à formuler les commentaires qui semblent pertinents même lorsque l'énoncé ne le demande pas explicitement.

Composition de l'épreuve

L'épreuve comporte un seul problème.

Préliminaire concernant la programmation. Il faudra écrire des fonctions ou des procédures à l'aide d'un langage de programmation qui pourra être soit Caml, soit Pascal, tout autre langage étant exclu. Indiquer en début de problème le langage de programmation choisi; il est interdit de modifier ce choix au cours de l'épreuve. Certaines questions du problème sont formulées différemment selon le langage de programmation ; cela est indiqué chaque fois que nécessaire. Par ailleurs, pour écrire une fonction ou une procédure en langage de programmation, le candidat pourra définir des fonctions ou des procédures auxiliaires qu'il explicitera, ou faire appel à d'autres fonctions ou procédures définies dans les questions précédentes.
Dans l'énoncé du problème, un même identificateur écrit dans deux polices de caractères différentes désigne la même entité, mais du point de vue mathématique pour la police écrite en italique (par exemple :

) et du point de vue informatique pour celle écrite en romain (par exemple : p).

Le but du sujet est d'étudier plusieurs algorithmes de recherche d'un mot, appelé motif, dans un texte.

Un alphabet

est un ensemble fini d'éléments appelés lettres. Un mot sur

est une suite finie, éventuellement vide, de lettres de

; la longueur d'un mot

est le nombre de lettres composant

; le mot de longueur nulle est noté

. L'ensemble des mots sur

est noté

. L'alphabet

utilisé est un sous-ensemble de l'alphabet usuel composé des 26 lettres de

. Si

est un mot, on note

la longueur de

; la notation

désigne la

lettre de

. Le mot

s'écrit donc :

. On dit que la lettre

est à la position

On dit qu'un mot

sur

est un facteur d'un mot

sur

s'il existe deux mots

sur

avec

, où

désigne le mot obtenu en concaténant

; on appelle alors position de

l'indice de

où

commence ; on dit que

figure dans

à la position

. Si

est le mot de longueur nulle, on dit que

est un préfixe de

; si

est le mot de longueur nulle, on dit que

est un suffixe de

. Il peut exister dans un mot plusieurs occurrences d'un même facteur. Le mot de longueur nulle,

, est considéré comme étant préfixe et suffixe de tout mot.

Dans tout l'énoncé, on considère deux mots

sur un alphabet

de longueurs non nulles, appelés respectivement texte et motif. On suppose que toute lettre de l'alphabet

apparaît au moins une fois dans

On veut résoudre le problème

( ) déterminer la position de chaque occurrence de dans .

On supposera toujours qu'on a:

; on ne vérifiera pas cette condition dans la programmation.
Par exemple, quand

est un facteur de

et figure aux positions 2,4 et 11 .

Indications pour la programmation

Caml

Les mots sont codés en utilisant le type string de Caml.
Si u est de type string et si

est un entier correspondant à un indice d'une lettre de

, string_length

renvoie le nombre de lettres de

. [i] est le caractère se trouvant dans u à l'indice i.

Fin des indications pour Caml

Pascal
On utilise les définitions suivantes:
const MAX_LONGUEUR = 100;
const MAX_SIGMA = 26;
type tab_char = array[0 .. MAX_LONGUEUR - 1] of char;
type tab_int_sigma = array[0 .. MAX_SIGMA - 1] of integer;
type pile = RECORD
    nb : integer;
    table : array[0 .. MAX_LONGUEUR - 1] of integer;
end;

La constante MAX_LONGUEUR donne la longueur maximum des mots considérés.
La constante MAX_SIGMA donne le nombre maximum de lettres de l'alphabet.
Les mots sont toujours codés en utilisant des tableaux de type tab_char ; les lettres du mot sont écrites consécutivement dans ce tableau à partir de l'indice

.
Fin des indications pour Pascal

Première partie : algorithme simple

1 - Soit

un entier positif ou nul vérifiant la relation

. Il s'agit d'écrire une fonction est_present qui permette de savoir si

figure dans

à la position s. La fonction parcourt les lettres du motif

de la gauche vers la droite et arrête la recherche dès que possible.
Caml : Écrire en Caml une fonction nommée est_present telle que, si :

m et t , de type string, codent et ,
s code l'entier s, alors est_present m t s renvoie le booléen true si figure dans à la position et le booléen false dans le cas contraire.
Pascal : Écrire en Pascal une fonction nommée est_present telle que, si :
m et t , de type tab_char, contiennent et ,
lm, de type integer, contient la longueur de ,
, de type integer, contient la valeur de , alors est_present (m, lm, t, s) renvoie le booléen true si m figure dans t à la position s et le booléen false dans le cas contraire.
2 - Préciser la complexité de la fonction est_present dans le pire cas et le meilleur cas.
3 - Il s'agit d'écrire une fonction nommée positions qui résout le problème ( ) en utilisant la fonction est_present.
Caml : Écrire en Caml la fonction positions telle que si et , de type string, codent et , alors positions m t renvoie une liste contenant les positions de dans .

Pascal : Écrire en Pascal la fonction positions telle que si :

m et t , de type tab_char, contiennent et ,
et , de type integer, contiennent les longueurs de et , alors positions(m, lm, renvoie un résultat de type pile contenant, dans le champ (ou membre) nb, le nombre de positions de dans et, dans le champ table, la liste des positions de dans .

4 - Préciser, pour une valeur de

quelconque et

quelconque, la complexité dans le pire cas de la fonction positions ; on exprimera cette complexité en fonction de

. Donner un exemple de deux mots

pour lesquels cette complexité est atteinte.

Deuxième partie : une amélioration de la méthode précédente

Dans la recherche simple, lorsque la recherche du motif

en position

est terminée, on poursuit la recherche en position

. On peut améliorer cet algorithme en poursuivant si possible la recherche un peu plus loin dans le texte

; pour cela, on suit la méthode décrite plus bas nommée algorithme amélioré.

On note

le cardinal de

. On numérote les lettres de

de 0 à

.
On suppose que l'on a défini en langage de programmation une fonction numero telle que :

en Caml, si , de type char, code une lettre de , numero renvoie le numéro de la lettre dans ;
en Pascal, si , de type char, code une lettre de , numero ( ) renvoie une valeur de type integer donnant le numéro de la lettre dans .
On ne demande pas d'écrire en langage de programmation la fonction numero. On suppose que cette fonction a une complexité constante.

On introduit un tableau

d'entiers défini comme suit. Si l'entier

vérifie

, la case d'indice

du tableau

contient la position de la dernière occurrence de la lettre de numéro

dans le motif

. Par convention, si cette lettre n'est pas présente dans le motif

, cette position est égale à -1 . Par exemple, pour

et pour le motif

, on a

, le numéro de la lettre

est 0 , celui de la lettre

est 1 , celui de la lettre

est 2 et le tableau

contient :

dans la case d'indice 0 , la valeur 3,
dans la case d'indice 1 , la valeur 1 ,
dans la case d'indice 2 , la valeur -1 .
- Il s'agit de construire le tableau en un temps linéaire en la longueur du motif . On justifiera la complexité linéaire de la construction du tableau .
Caml : Écrire en Caml une fonction nommée calcul_D telle que, si :
, de type string, code le motif ,
nbSigma contient le nombre de lettres de l'alphabet , alors calcul_D m nbSigma renvoie un vecteur (ou tableau) codant le tableau .
Pascal : Écrire en Pascal une fonction nommée calcul_D telle que, si :
m, de type tab_char, contient ,
lm, de type integer, contient la longueur de ,
nbSigma, de type integer, contient le nombre de lettres de l'alphabet ,

Pour décrire l'algorithme amélioré, on introduit la notion de fenêtre de recherche. Cette fenêtre dépend d'un indice

vérifiant

; cette fenêtre contient les

lettres consécutives de

comprises entre les indices

; ces lettres sont mises en regard avec les

lettres du motif

. On dit alors que la fenêtre est à la position

. Dans l'algorithme, la fenêtre se déplace toujours de la gauche vers la droite ; le motif se déplace avec la fenêtre alors que le texte ne bouge pas.
On considère l'exemple défini par :

Au départ de l'algorithme amélioré,

et la fenêtre de recherche est en gris sur la figure 1 .

Indices	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14

Figure 1 : fenêtre de recherche à la position 0

On examine cette position de la fenêtre en comparant le facteur

qui est dans la fenêtre avec le motif

qui est en regard et on constate que ce facteur n'est pas une occurrence de

dans

.
On considère alors la lettre de

qui se trouve à droite de la fenêtre de recherche ; c'est la lettre

à l'indice 4 de

en gras sur la figure 1 ; on note clé cette lettre. On remarque que si on considère la fenêtre de recherche positionnée à l'indice 1 ou à l'indice 2 , la lettre du motif m1 qui se trouve en regard de clé n'est pas la lettre

, c'est la lettre

dans les deux cas : l'examen de ces deux positions de la fenêtre ne permettrait pas de découvrir une occurrence du motif dans le texte. C'est pourquoi on n'examine pas les positions 1 et 2 de la fenêtre. En revanche, si on met la fenêtre en position 3, clé est en regard de la dernière apparition de la lettre

dans

, en gras sur la figure 1 ; on retient cette position pour savoir si le motif figure on non à l'indice 3 du texte.

La fenêtre de recherche est maintenant en gris sur la figure 2 :

Indices	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14

Figure 2 : fenêtre de recherche à la position 3

On examine la fenêtre et on constate que

contient une occurrence de

à la position 3 .
Maintenant, clé est la lettre de

qui se trouve à l'indice 7 en gras sur la figure 2 : il s'agit de la lettre

. On déplace la fenêtre pour que clé se trouve en regard de la dernière occurrence de la lettre

dans

, en gras sur la figure 2 ; on déplace en conséquence la fenêtre d'une seule case, elle se trouve alors à la position 4 et est représentée sur la figure 3 . On examine la fenêtre et on constate que

ne contient pas une occurrence de

à l'indice 4 .

Indices	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14

Figure 3 : fenêtre de recherche à la position 4

On continue avec le même principe pour trouver d'autres éventuelles occurrences de

dans t1. Maintenant, clé est la lettre de

qui se trouve à l'indice 8 , en gras sur la figure 3 : il s'agit de la lettre

. Le déplacement suivant consistera à décaler la fenêtre vers la droite en n'examinant pas les positions qui mettraient en regard de clé une lettre de

différente de la lettre

.
6 - Dans l'exemple de la figure 3, indiquer la prochaine position de la fenêtre de recherche et dire si cette position correspond ou non à une occurrence de

dans

.
7 - Décrire la suite du déroulement de l'algorithme appliqué à Exemple1 jusqu'à ce qu'on puisse conclure que toutes les occurrences de

dans

ont été déterminées. On poursuivra les déplacements de la fenêtre vers la droite en utilisant le même principe que précédemment.
8 - On revient au déroulement de l'algorithme amélioré dans le cas général. On suppose que la fenêtre est à la position

et que l'on a

. En utilisant le tableau

et la fonction numero décrits plus haut, indiquer la position suivante de la fenêtre.
9 - Il s'agit d'écrire une fonction positions2 qui résout le problème

en appliquant l'algorithme amélioré.
Caml : Écrire en Caml la fonction positions2 telle que si :

m et t , de type string, codent et ,
nbSigma contient le nombre de lettres de l'alphabet ,
alors positions2 m nbSigma renvoie une liste contenant les positions de dans déterminées selon l'algorithme amélioré.
Pascal : Écrire en Pascal la fonction positions2 telle que si :
m et t , de type tab_char, contiennent et ,
et , de type integer, contiennent les longueurs de et ,
nbSigma, de type integer, contient le nombre de lettres de l'alphabet , alors positions2(m, lm, , lt, nbSigma) renvoie un résultat de type pile contenant, dans le champ nb, le nombre de positions de dans et, dans le champ table, la liste des positions de dans déterminées selon l'algorithme amélioré.

10 - Préciser, en fonction de

, la complexité dans le meilleur cas de la fonction positions2. On ne prendra pas en compte la complexité du calcul du tableau

. Donner un exemple qui atteint cette complexité.

Dans toute la suite, on se propose de résoudre le problème (

) à l'aide d'automates.
Un automate

est décrit par un quintuplet (

), où :

est un alphabet ;
est un ensemble fini et non vide appelé ensemble des états de ;
est appelé ensemble des états initiaux de ;
est appelé ensemble des états finals de ;
est appelé l'ensemble des transitions; étant donnée une transition , on dit qu'elle va de l'état à l'état et qu'elle est d'étiquette ; on pourra la noter ; on dit aussi que est l'origine de la transition et son extrémité.

Un calcul de

est une suite de la forme

où, pour

est une transition;

est l'origine du calcul,

son extrémité. L'étiquette du calcul est le mot

formé par la suite des étiquettes des transitions successives.
Un calcul de

est dit réussi si son origine est dans

et son extrémité dans

. Un mot

sur

est reconnu par

s'il est l'étiquette d'un calcul réussi. Le langage reconnu par

, noté

, est l'ensemble des mots reconnus par

L'automate

est dit déterministe si

contient exactement un élément et si, pour tout

et tout

, il existe au plus un état

avec

.
L'automate

est dit complet si, pour tout

et tout

, il existe au moins un état

.
Si

est un automate déterministe complet, on définit sa fonction de transition

dans

par:

si et seulement si

. On définit alors, récursivement, une fonction

de (

) dans

par :

si ,
si et .

Dans tout le sujet, les automates considérés auront un seul état initial. On notera

le nombre d'états d'un automate; les états seront numérotés de 0 à

. L'état initial possédera toujours le numéro

. Si

est le numéro d'un état, on dira qu'il s'agit de l'état

, identifiant ainsi un état avec son numéro.

Un automate peut être représenté par un dessin comme il est fait ci-dessous pour représenter l'automate Aex, qui est déterministe et non complet.

Aex possède trois états : 0,1 et 2 .
L'état 0 est l'état initial.
Aex possède un seul état final, l'état 2 .
Aex possède trois transitions, les transitions

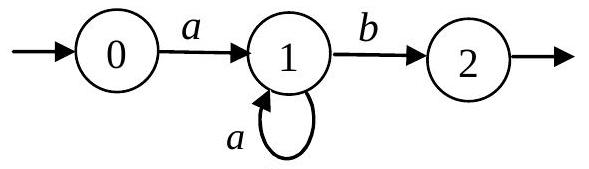
Figure 4 : l'automate Aex

Troisième partie : implémentation d'un automate

L'automate Aex représenté sur la figure 4 sert d'exemple ci-dessous pour illustrer le codage d'un automate en langage de programmation.

Indications pour Caml

On utilise une constante définie par :
let MAX_Q = 100 ;;
MAX_Q donne le nombre maximum d'états des automates considérés.

Pour représenter l'ensemble des états finals d'un automate, on utilise une liste, de type int list, qui contient les numéros des états finals.
Si

est un état d'un automate, une transition d'origine

est codée par un couple de type (char * int) contenant l'étiquette de cette transition et le numéro de l'extrémité de cette même transition.
Si

est un état d'un automate, on représente l'ensemble des transitions d'origine

par la liste des transitions d'origine

; cette liste est de type (char * int) list.
L'ensemble des transitions d'un automate

est codé par un vecteur ; si

vérifie les inégalités

, l'élément d'indice

de ce vecteur contient la liste des transitions d'origine

. Ce vecteur est ainsi en Caml de type (char * int) list vect.
Pour définir un automate

, on utilise le type enregistrement (type produit) suivant :

type automate = {nbQ : int;
        F : int list;
        T : (char * int) list vect;
    };;

dans lequel les champs (ou membres) correspondent:

pour nbQ, au nombre d'états de ,
pour F , à la liste des états finals de ,
pour T, à l'ensemble des transitions de .

L'automate Aex de la figure 4 peut être défini par :
let T_Aex = make_vect 3 [];;
T_Aex. (0) <- [(a,1)];
T_Aex.(1) <- [(a,1); (b,2)];;
let Aex = {nbQ = 3 ; F = [2]; T = T_Aex};;
Fin des indications pour Caml

Indications pour Pascal
On ajoute les définitions suivantes aux définitions données plus haut :
const MAX_Q = 100;
type transition = RECORD
    etiquette : char;
    extremite : integer;
end;
type tab_int_Q = array[0 .. MAX_Q - 1] of integer;
type tab_transition = array[0 .. MAX_SIGMA - 1] of transition;
type tab_tab_transition = array[0 .. MAX_Q - 1] of tab_transition;
type automate = RECORD
        nbQ : integer;
        nbF : integer;
        F : tab_int_Q;
        nbT : tab_int_Q;
        T : tab_tab_transition;
end;

La constante MAX_Q donne le nombre maximum d'états des automates considérés.

est un état d'un automate, une transition d'origine

est codée par un enregistrement de type transition, le champ (ou membre) etiquette contenant l'étiquette de cette transition et le champ extremite le numéro de l'extrémité de cette même transition.
Si

est un état d'un automate, on représente l'ensemble des transitions d'origine

en utilisant un tableau de type tab_transition (on ne codera que des automates déterministes avec le type automate).
L'ensemble des transitions d'un automate est codé par un tableau de type tab_tab_transition, la case d'indice

de ce tableau contenant la liste des transitions d'origine

.
Un automate déterministe

sera codé par un enregistrement de type automate dans lequel les champs (ou membres) correspondent :

pour nbQ, au nombre d'états de ;
pour nbF, au nombre d'états finals de ;
pour F , à un tableau contenant la liste des états finals de ;
pour nbT, à un tableau donnant les nombres de transitions issues de chaque état ; plus précisément, si p est compris entre 0 et nbQ - contient le nombre de transitions d'origine ;
pour T, à l'ensemble des transitions de .

L'automate Aex de la figure 4 peut être défini par une variable Aex de type automate avec les instructions:

Aex.nbQ := 3;
Aex.nbF := 1;
Aex.F[0]:= 2;
Aex.nbT[0] := 1;
Aex.T[0][0].etiquette := 'a';
Aex.T[0][0].extremite := 1;
Aex.nbT[1] := 2;
Aex.T[1][0].etiquette := 'a';
Aex.T[1][0].extremite := 1;
Aex.T[1][1].etiquette := 'b';
Aex.T[1][1].extremite := 2;
Aex.nbT[2] := 0;
Fin des indications pour Pascal

Soit

un automate déterministe sur un alphabet

.
11 - Il s'agit de savoir si un état est final ou non. On rappelle qu'un état est identifié avec son numéro.
Caml : Écrire en Caml une fonction nommée est_final telle que si :

A, de type automate, code l'automate ,
p est un entier codant un état de , alors est_final A p renvoie le booléen true si est un état final de et false sinon. Indiquer la complexité de cette fonction.
Pascal : Écrire en Pascal une fonction nommée est_final telle que si :
A, de type automate, code l'automate ,
p , de type integer, contient un état de , alors est_final(A, p) renvoie un booléen qui vaut true si est un état final de et false dans le cas contraire. Indiquer la complexité de cette fonction.
- On suppose que est un état et une lettre ; on veut connaître l'état atteint à partir de l'état par la transition d'étiquette si cette transition existe.
On rappelle que le cardinal de l'alphabet est majoré par une constante (égale à 26).
Caml : Écrire en Caml une fonction nommée etat_suivant telle que si :
A, de type automate, code l'automate ,
p est un entier codant un état de ,
x est une lettre appartenant à ,
alors etat_suivant A renvoie un entier codant l'état tel que ( ) soit une transition de si cette transition existe et -1 sinon. Indiquer la complexité de cette fonction.
Pascal : Écrire en Pascal une fonction nommée etat_suivant telle que si :
A, de type automate, code l'automate ,
p , de type integer, contient le numéro d'un état de ,
x, de type char, contient une lettre appartenant à , alors etat_suivant renvoie une valeur de type integer contenant l'état tel que ( ) soit une transition de si cette transition existe et -1 sinon. Indiquer la complexité de cette fonction.

13 - Il s'agit de déterminer l'état, s'il existe, qui est extrémité du calcul dont l'origine est l'état initial et dont l'étiquette est un mot donné.
Caml : Écrire en Caml une fonction nommée execution telle que si :

A, de type automate, code l'automate ,
u, de type string, code un mot sur , alors execution A u renvoie un entier codant l'état qui est l'extrémité du calcul dont l'origine est l'état initial et dont l'étiquette est , si existe, et -1 sinon. Indiquer la complexité de cette fonction.
Pascal : Écrire en Pascal une fonction nommée execution telle que si :
A, de type automate, code l'automate ,
u, de type tab_char, contient un mot sur ,
lu, de type integer, contient la longueur de , alors execution( ) renvoie une valeur de type integer donnant l'état qui est extrémité du calcul dont l'origine est l'état initial et dont l'étiquette est , si existe, et -1 sinon. Indiquer la complexité de cette fonction.

14 - Il s'agit de savoir si un mot est reconnu ou non par un automate.
Caml : Écrire en Caml une fonction nommée reconnait telle que si :

A, de type automate, code l'automate ,
u, de type string, code le mot sur , alors reconnait A u renvoie le booléen true si le mot est reconnu par et false sinon. Indiquer la complexité de cette fonction.
Pascal : Écrire en Pascal une fonction nommée reconnait telle que si :
A, de type automate, code l'automate ,
u, de type tab_char, contient le mot sur ,
lu, de type integer, contient la longueur de , alors reconnait (A, u, lu) renvoie le booléen true si le mot est reconnu par et false sinon. Indiquer la complexité de cette fonction.
- On considère un automate A déterministe complet sur un alphabet , un état de et une lettre de . L'objectif de la question est de concevoir une fonction permettant de modifier l'extrémité de la transition d'origine et d'étiquette .
Caml : On considère une liste, nommée trans, de type (char * int) list, codant l'ensemble des transitions d'origine . Écrire en Caml une fonction remplace telle que, si :
code la lettre ,
q code un état de ,
alors remplace trans renvoie une liste identique à trans sauf que le couple contenant l'étiquette est remplacé par le couple ( ). Indiquer la complexité de cette fonction.
Pascal : On considère un tableau, nommé trans, de type tab_transition, codant l'ensemble des transitions d'origine . Écrire en Pascal une fonction remplace telle que, si :
x , de type char, contient la lettre ,
q, de type integer, contient un état de , alors remplace( , trans, ) renvoie un tableau de type tab_transition identique à trans sauf que le couple contenant l'étiquette est remplacé par le couple ( ). Indiquer la complexité de cette fonction.

Quatrième partie : utilisation d'automates.

On considère un mot

sur

- Dessiner un automate déterministe comportant

états reconnaissant le langage réduit au seul mot

. On note

cet automate.

- Il s'agit de construire l'automate

en langage de programmation.
Caml : Écrire en Caml une fonction nommée automate_de_mot telle que, si m, de type string, code le mot

, alors automate_de_mot

renvoie un résultat de type automate codant l'automate

.
Pascal : Écrire en Pascal une fonction nommée automate_de_mot telle que, si :

m, de type tab_char, contient le mot ,
lm, de type integer, contient la longueur de , alors automate_de_mot( ) renvoie un résultat de type automate codant l'automate .

18 - Il s'agit d'utiliser l'automate

pour déterminer si un mot

sur

est préfixe du mot

.
Caml : Écrire en Caml une fonction nommée est_prefixe telle que, si

, de type string, codent les mots

, alors est_prefixe m u renvoie le booléen true quand

est préfixe de

et false dans le cas contraire.
On utilisera les fonctions automate_de_mot et execution.

Pascal : Écrire en Pascal une fonction nommée est_prefixe telle que, si :

m et u , de type tab_char, contiennent les mots et ,
et , de type integer, contiennent les longueurs de et , alors est_prefixe(m, lm, u, lu) renvoie le booléen true quand est préfixe de et false dans le cas contraire.
On utilisera les fonctions automate_de_mot et execution.
- On s'intéresse à présent au langage composé des mots dont est suffixe. On le note . Montrer que ce langage est rationnel.

20 - Expliquer comment on peut modifier l'ensemble des transitions de

pour obtenir un automate non déterministe reconnaissant

. On note

cet automate. On considère le cas où

. Dessiner l'automate

21 - Déterminiser l'automate

dessiné à la question précédente. On utilisera pour cela un algorithme de déterminisation d'automate.

Soit

un texte et

un motif. On note

un automate déterministe complet reconnaissant le langage

; on suppose que

a un seul état final.

- Décrire les principes d'un algorithme utilisant l'automate

pour résoudre le problème

. L'algorithme devra avoir une complexité de l'ordre de la longueur de

. Justifier la validité de cet algorithme avec soin.

- Il s'agit de programmer l'algorithme précédent.
Caml : On suppose que l'on dispose d'une fonction DS telle que, si

est de type string, alors DS m renvoie un résultat de type automate codant l'automate

. En utilisant cette fonction, écrire en Caml une fonction nommée positions3 telle que, si m et t , de type string, codent le motif

et le texte

, alors positions 3 m t résout le problème

, c'est-à-dire renvoie une liste contenant les positions du motif

dans le texte

.
Pascal : On suppose que l'on dispose d'une fonction DS telle que, si :

m, de type tab_char, contient le mot ,
, de type integer, contient la longueur de , alors renvoie un résultat de type automate codant l'automate . En utilisant cette fonction, écrire en Pascal une fonction nommée positions3 telle que, si :
m et t , de type tab_char, contiennent et ,
et , de type integer, contiennent les longueurs de et , alors positions3(m, lm, t , lt) résout le problème ( ), c'est-à-dire renvoie un résultat de type pile contenant, dans le champ nb, le nombre de positions de dans et, dans le champ table, la liste des positions du motif dans le texte .

Cinquième partie : automate des suffixes

Le but de cette la partie est d'écrire un automate déterministe complet, avec un seul état final, reconnaissant le langage

On considère un alphabet

et un mot

sur

.
On note

l'ensemble des préfixes de

.
Soit

l'application de

dans

définie par : pour tout mot

sur

est le plus long mot à la fois suffixe de

et préfixe de

.
24 - Préciser

pour tout mot

quand

est réduit à une seule lettre

.
On revient au cas général :

est un mot quelconque sur

.
25 - Soit

. Montrer que

si et seulement si

.
26 - Préciser

. Préciser

quand

est un préfixe de

.
27 - Montrer que

pour tout mot

et toute lettre

.
On définit un automate déterministe et complet sur l'alphabet

, noté

, de la façon suivante :

les états de sont les préfixes de ,
l'état initial de est ,
l'état final de est ,
pour tout préfixe de et toute lettre , ( ) est une transition de et n'admet pas d'autres transitions que les transitions de cette forme.
Convention : on numérote les états de ; l'état initial est noté 0 et pour compris entre 1 et , le préfixe est noté .
28 - On suppose que l'on a . Dessiner l'automate .
Indication : cet automate n'a qu'un seul état, noté 0.
29 - On suppose que l'on a et on considère le mot . Dessiner l'automate en représentant les états par leurs numéros.
Indication : cet automate a trois états, les états , numérotés 0,1 et 2 .
30 - On considère l'automate et un mot sur ; on note la fonction de transition de . Montrer l'égalité .
31 - Montrer que reconnaît le même langage que , c'est-à-dire .

Soit

un mot sur

une lettre de

. On pose

. On note

. On admet les propriétés suivantes de la fonction

.
Soit

un préfixe de

une lettre.
(i) Si

est préfixe de

.
(ii) Si

quand

.
(iii) Si

.
32 - Donner des règles simples de construction pour passer de

.
33 - On considère le cas

et le mot

. Illustrer les règles énoncées à la question précédente en traçant l'automate

à partir de l'automate

obtenu à la question 29.
34 - Il s'agit de programmer la fonction DS pour l'alphabet

.
Caml : Écrire en Caml une fonction nommée DS telle que, si

, de type string, code un mot

, alors DS

renvoie un résultat, de type automate, codant l'automate

. On supposera si nécessaire qu'on a défini une constante entière MAX_LONGUEUR et que les mots considérés ont au plus MAX_LONGUEUR lettres.
Pascal : Écrire en Pascal une fonction nommée DS telle que, si :

m, de type tab_char, contient le mot sur ,
, de type integer, contient la longueur de , alors DS(m, lm) renvoie un résultat, de type automate, codant l'automate .
35 - On revient à un alphabet quelconque. Donner la complexité de la fonction positions3.