Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

L'anémométrie à fil chaud

L'anémométrie à fil chaud est une technique permettant de mesurer la vitesse d'écoulement d'un fluide. Elle est basée sur l'influence de la vitesse d'écoulement du fluide sur le transfert thermique conductoconvectif d'un solide conducteur plongé dans ce fluide.
Le système le plus couramment utilisé est un petit fil cylindrique, d'un diamètre typique

de l'ordre de quelques micromètres, parcouru par un courant et donc chauffé par effet Joule.
Ce petit fil est fixé à des broches d'alimentation par l'intermédiaire d'une gaine d'adaptation qui permet notamment l'alimentation du fil et de fixer la longueur active du fil, notée

qui est ici de l'ordre de quelques millimètres.
Quelques valeurs numériques concernant certaines caractéristiques physiques du fil chaud sont rassemblées dans le tableau ci-dessous.

Figure 1 - Anémomètre

Matériau	Résistivité à	Conductivité thermique :	Masse volumique :	Capacité thermique massique :
Tungstène	5,5	1,9	1,93	0,14
Platine	9,8	0,72	2,15	0,13
Platine-iridium	32	0,17	2,16	0,13

Les applications numériques seront réalisées avec au plus 2 chiffres significatifs.

I Étude énergétique de l'anémomètre

I.A Bilan d'énergie dans le fil chaud

Le fil conducteur (en tungstène par exemple) est parcouru par un courant électrique continu d'intensité

. Il est plongé dans un fluide en écoulement. On utilisera les notations suivantes :

Caractéristiques du fil (que l'on repère avec l'indice « w » pour wire en anglais) : masse volumique , capacité thermique massique , température , résistivité (inverse de la conductivité) électrique , conductivité thermique , longueur et diamètre .
Caractéristiques du fluide (généralement de l'air que l'on repère lorsqu'il a ambiguïté avec l'indice «f z pour fluide) et de l'écoulement : masse volumique , viscosité , température , pression , vitesse de l'écoulement . Ces caractéristiques sont supposées constantes pendant la mesure.
Si l'on note le coefficient de transfert thermique conducto-convectif, la puissance thermique surfacique cédée par le fil au fluide à travers la surface est donnée par la loi de Newton :

On notera (

) l'axe du fil, ses extrémités étant situées en

1. Rappeler la loi d'Ohm locale. Définir les grandeurs intervenant dans cette loi et donner leurs unités usuelles. Établir l'expression de la résistance électrique totale, notée , du fil en fonction de et .
  En déduire la puissance dissipée par effet Joule dans le fil en fonction de et , puis la puissance volumique dissipée par effet Joule : .
1. Rappeler la loi de Fourier de la conduction thermique. Définir les grandeurs intervenant dans cette loi. On dit souvent qu'il s'agit d'une loi phénoménologique. Que cela signifie-t-il ? La température est supposée homogène sur chaque section du fil d'abscisse . Que peut-on en déduire?
  Établir l'équation de diffusion thermique dans le cas d'un fil à la température où seuls les transferts thermiques par conduction ont lieu.
  On se place en régime permanent dans tout le reste de la partie et on suppose la vitesse de l'écoulement uniforme et indépendant du temps. En plus des transferts thermiques par conduction, on prend en compte les transferts thermiques par conducto-convection et ceux provenant de l'effet Joule. Les transferts thermiques sont intégrés dans le terme conductoconvectif.
1. Dans la loi de Newton (1), la grandeur dépend de la vitesse de l'écoulement. Quelle est son unité? Expliquer qualitativement comment varie en fonction de . Expliquer alors comment évolue quand augmente.
  . En effectuant un bilan énergétique sur un élément de volume de fil compris entre les abscisses et , établir l'équation aux dérivées partielles vérifiée par la température .

La résistivité du fil dépend en fait de la température

de ce dernier. Expérimentalement, on mesure que si le fil est en contact avec un fluide à la température

, sa résistivité

vérifie la relation :

où

est sa résistivité à la température du fluide et

est un coefficient expérimental supposé constant. On note enfin

. Mettre l'équation obtenue à la question 4 sous la forme :

Exprimer les constantes

en fonction de l'intensité

et des caractéristiques du fil, du fluide et de l'écoulement. On montrera, en particulier, que

. Dans la plupart des anémomètres à fil chaud,

est négatif. Déterminer la condition correspondante sur le coefficient conducto-convectif

. On se place dans ce cas dans toute la suite et on pose:

On considère que le contact thermique assuré par les gaines d'adaptation entre les extrémités du fil et les broches de l'anémomètre (voir figure 1) se fait sans résistance thermique (contact parfait). Les broches et les gaines sont à la température

du fluide.

1. Rappeler la définition d'une résistance thermique ainsi que son unité. Quelle est la conséquence d'un contact sans résistance thermique?
  Déterminer la solution générale de l'équation différentielle (3).
  En tenant compte des conditions aux limites dans le problème et de sa symétrie, montrer que s'exprime assez simplement à partir de la fonction cosinus hyperbolique. En déduire l'expression du profil de température dans le fil de la sonde en fonction de et .
1. Déterminer la puissance thermique cédée par le fil à l'ensemble des deux gaines d'adaptation en fonction de et .
1. Montrer que la moyenne spatiale de la température du fil s'écrit selon la relation

dans laquelle on précisera l'expression du paramètre

.
La figure 2 représente la distribution de température dans le fil chaud pour différentes valeurs du rapport

. La fonction tracée est

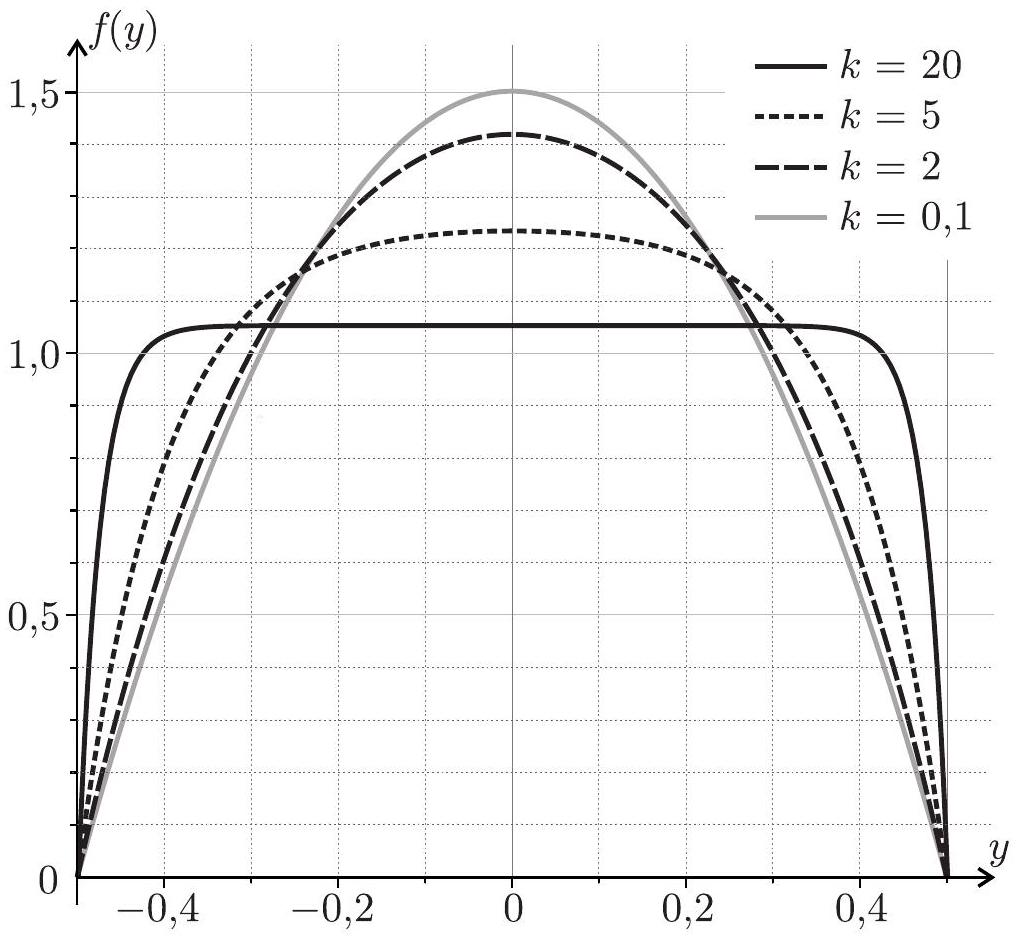
Figure 2 - Représentation graphique de la fonction

pour quatre valeurs du paramètre

1. Pour un fil de tungstène de diamètre , de longueur et fonctionnant dans un régime de température tel que , évaluer, en faisant les approximations pertinentes, la valeur numérique du coefficient

où

est la température maximale atteinte dans le fil. En exploitant la figure 2, commenter la valeur trouvée.

I.B Puissance thermique cédée au fluide

1. Commenter les courbes de la figure 2. Quelle approximation peut-on faire quant à la température dans le cas d'un fil long (on précisera ce que «long» signifie ici) ?

La résistivité

du fil est toujours supposée dépendre de la température du fluide avec lequel il est en contact selon la relation (2).

1. Calculer la résistance d'un fil supposé long en fonction de sa résistance à la température , de et des températures et .

Toujours dans le cadre d'un fil long, on fait l'hypothèse que la puissance thermique

cédée par le fil aux deux gaines d'adaptation est négligeable devant la puissance

dissipée par effet Joule le long du fil ou celle, notée

, correspondant aux échanges thermiques conducto-convectifs reçus par le fluide à l'interface entre le fil et le fluide.

. Déterminer, en régime permanent, l'expression de

en fonction de la différence

.
Pour un fluide de viscosité

et de masse volumique

, qui s'écoule à la vitesse

autour d'un obstacle fixe de taille caractéristique

, on définit le nombre de Reynolds

. Il compare deux modes de transport au sein du fluide.

1. Sachant que la viscosité s'exprime en déterminer la dimension de .

On définit par ailleurs le nombre de Nusselt,

1. Déterminer la dimension de et proposer une interprétation physique de cette quantité. Comment varie lorsque la vitesse du fluide s'écoulant autour du fil augmente?

On admet que le nombre de Nusselt vérifie la loi de King

où

sont des constantes connues qui ne dépendent que de la nature du fluide en écoulement.

. En exploitant l'expression de

obtenue à la question 8 et les résultats de la question 5 , montrer que dans le cas d'un fil long on peut écrire

On précisera la valeur numérique de l'exposant

. On considère de nouveau un fil de longueur

quelconque. Établir l'expression de la puissance thermique

associée au transfert conducto-convectif du fil vers le fluide.

On suppose que la relation (4) reste valable en ordre de grandeur pour un fil de longueur quelconque et que, de plus, le coefficient

qu'elle fait intervenir est de l'ordre de l'unité pour toutes les mesures effectuées.

1. En étudiant le rapport , et sachant que dans le contexte d'étude SI, justifier a posteriori que l'on puisse simplifier le problème en ne considérant pas les pertes dans les gaines d'adaptation sous l'hypothèse d'un fil long.
  En utilisant le résultat de la question 12 et en supposant que l'on puisse appliquer la loi de King, montrer que, pour un fil long, la mesure de la vitesse du fluide se ramène à une mesure de résistance. On déterminera l'expression de en fonction notamment de et .

II Anémométrie à deux fils

On étudie à présent une autre technique qui utilise deux fils parallèles séparés par une distance

comme représenté sur la figure 3 ci-dessous.
Cette technique est plus précise que la précédente car elle permet de faire deux mesures : la première n'utilise que le premier fil; la seconde étudie la réponse induite par le premier dans le second.

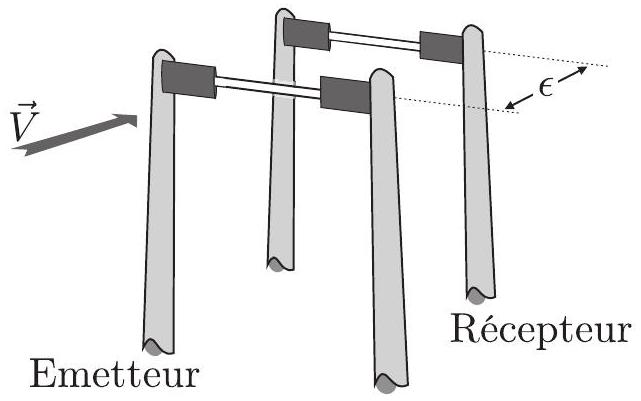
Figure 3 - Disposition des 2 fils.

Le premier fil (l'émetteur, repéré par un indice e), froid initialement (c'est-à-dire à la température du fluide environnant ), est traversé par une impulsion électrique d'intensité et d'une durée de quelques , appelée « phase de chauffe», à l'issue de laquelle le fil s'est donc échauffé.
On fait ensuite passer dans l'émetteur un faible courant , dont on négligera l'influence thermique, et on mesure la tension à ses bornes en fonction du temps. On obtient ainsi l'évolution de la résistance électrique en fonction du temps et donc celle de sa température .
Un second fil (le recepteur, repéré par un indice r) est placé parallèlement au premier, en aval dans l'écoulement du fluide (ici de l'air), à une distance du premier. Sous l'action de l'écoulement, une trainée d'air chaud (zone échauffée du fluide par l'impulsion thermique de l'émetteur) va atteindre le récepteur.
L'acuité et la durée de cette trainée d'air chaud vue par le second fil vont dépendre notamment de la norme de la vitesse de l'air.

Hormis leur température et donc leur résistance, les caractéristiques de ces deux fils sont supposées identiques à celles du fil utilisé dans la partie

.
On se concentre tout d'abord sur le fil émetteur de l'impulsion thermique afin d'étudier la première possibilité de mesure de la vitesse de l'écoulement. On néglige la conduction thermique dans le fil et entre le fil et les broches. On suppose donc, conformément à ce qui a été fait précédemment, que la température du fil est homogène et ne dépend que du temps, tout comme sa résistance toujours obtenue dans le cadre du modèle de résistivité résumé par la relation (2). Pendant la phase de chauffe, l'impulsion étant très brève, on négligera les pertes d'énergie dues à la convection de l'air autour du fil lors de cette phase. L'origine des temps

correspond au début de l'impulsion électrique.

1. Montrer que, pendant la phase de chauffe, la température vérifie une équation différentielle qui peut se mettre sous la forme

où l'on exprimera la durée caractéristique

de montée en température et le paramètre

en fonction des paramètres du problème. Que représente

1. Résoudre cette équation en exprimant finalement en fonction de et . En déduire, en fonction de et , l'expression de l'amplitude de l'impulsion thermique obtenue dans le fil émetteur après qu'il a été parcouru par l'impulsion de courant.
1. Une fois l'impulsion terminée, i. e. pour , le fil émetteur ne reçoit plus de courant qui le chauffe, il se refroidit par convection au contact thermique de l'air en mouvement. Déterminer la température de l'émetteur durant cette phase dite de relaxation en fonction de ainsi que d'une nouvelle durée caractéristique de cette phase de relaxation dépendant notamment de .

Sur la figure 4 ci-dessous le graphe de gauche indique l'allure de

mesurée lors des phases de chauffe et de relaxation au contact de deux écoulements de vitesse différente.

Sur cette même figure 4, le graphe de droite montre de façon plus quantitative en échelle semilogarithmique, des relevés expérimentaux de la phase de relaxation pour différentes valeurs de la norme de la vitesse de l'écoulement.

Figure 4 - Mesures au niveau de l'émetteur. Sur la figure de droite on a représenté les mesures et leurs différentes régressions linéaires.

1. Pendant la phase de chauffe, on constate sur la partie gauche de la figure 4 que les deux courbes sont confondues. Quelle hypothèse émise plus haut ce résultat permet-il de confirmer?
1. Expliquer qualitativement comment l'analyse des courbes de la figure 4 permet une première mesure de la norme de la vitesse de l'écoulement du fluide.

L'air réchauffé par l'émetteur va être transportée par convection jusqu'au second fil, le récepteur. En alimentant ce dernier par un très faible courant

, dont on peut toujours négliger l'influence thermique, on peut mesurer sa résistance et en déduire sa température.

Certains résultats expérimentaux sont rassemblés dans la figure 5 sur la page suivante

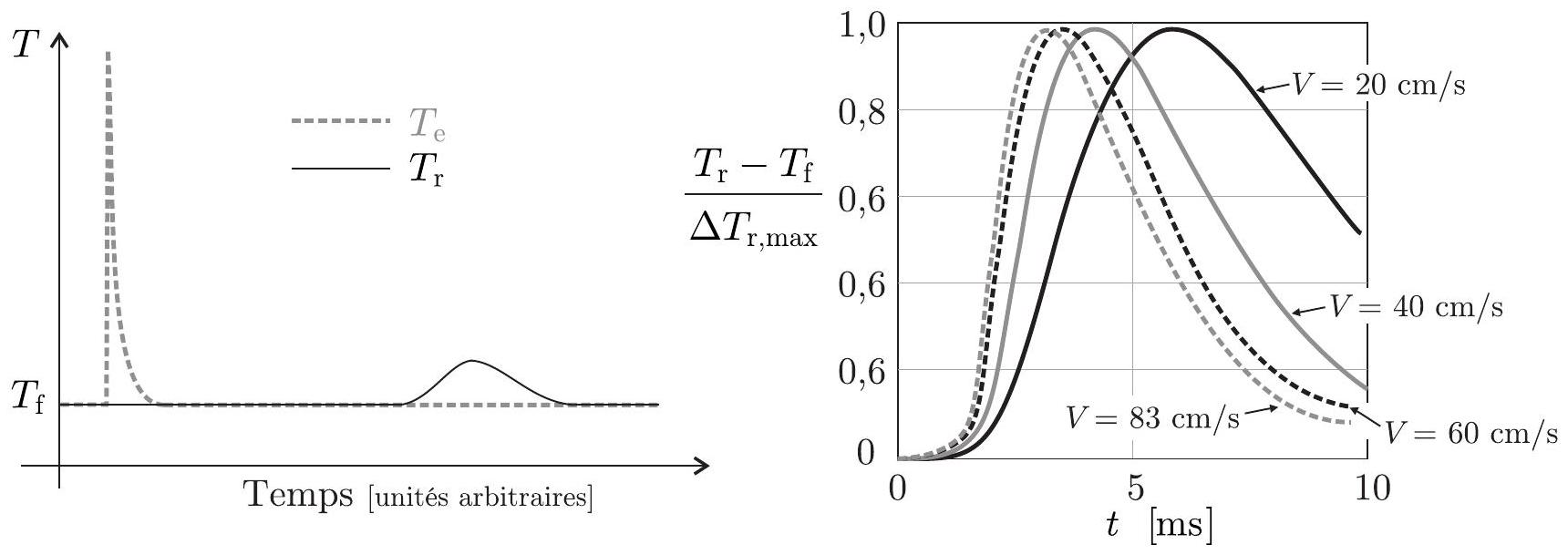
Figure 5 - Analyse des températures.

Sur la partie gauche de la figure 5, on a représenté avec les mêmes échelles de temps et d'amplitude l'allure typique des pics de températures relevés dans chacun des deux fils.

De façon plus quantitative, on a représenté sur la partie droite de cette même figure, le résultat des mesures de l'évolution de la fonction normalisée

pour différentes valeurs de la norme de la vitesse de l'écoulement.

1. Commenter les deux courbes de la partie gauche de la figure 5. Proposer des explications qualitatives pour les différents phénomènes que l'on peut observer.
1. Expliquer qualitativement comment l'analyse des courbes de la figure 5 permet une seconde mesure de la norme de la vitesse de l'écoulement du fluide.

FIN DE L'ÉPREUVE

1. Ils ont été collectés dans l'article «Pulsed-wire technique for velocity measurements in natural convection flow - a numerical optimisation tool , Grignon et al., 1998, International Journal of Heat and Mass Transfer, volume 41, p. 3121-3129.

Mines Physique 1 MP 2022

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL. Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).

L'anémométrie à fil chaud

I Étude énergétique de l'anémomètre

I.A Bilan d'énergie dans le fil chaud

I.B Puissance thermique cédée au fluide

II Anémométrie à deux fils

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL.
Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).