Version interactive avec LaTeX compilé
A 2001 PHYS. PC I
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE, ÉCOLE POLYTECHNIQUE (FILIÈRE TSI) CONCOURS D'ADMISSION 2001
PREMIÈRE ÉPREUVE DE PHYSIQUE
Filière PC
(Durée de l'épreuve :
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPE-EIVP.
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE I - Filière PC
Cette épreuve comprend 4 pages de texte.
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPE-EIVP.
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE I - Filière PC
Cette épreuve comprend 4 pages de texte.
- Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
- Tout résultat fourni dans l'énoncé peut être utilisé.
- Il ne faudra pas hésiter à formuler tout commentaire qui vous semblera pertinent, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.
Conventions typographiques : un vecteur est noté en gras (A), sa norme en italique
L'épreuve comprend trois problèmes indépendants les uns des autres, et que l'on pourra traiter dans l'ordre de son choix. Les deux derniers sont inspirés du film de Brian de PALMA Mission to Mars, diffusé en France en mai 2000.
1. La relation de BERNOULLI
On considère un référentiel galiléen
Fluide en translation uniforme
2 - Le fluide se déplace maintenant en bloc dans
Fluide accéléré
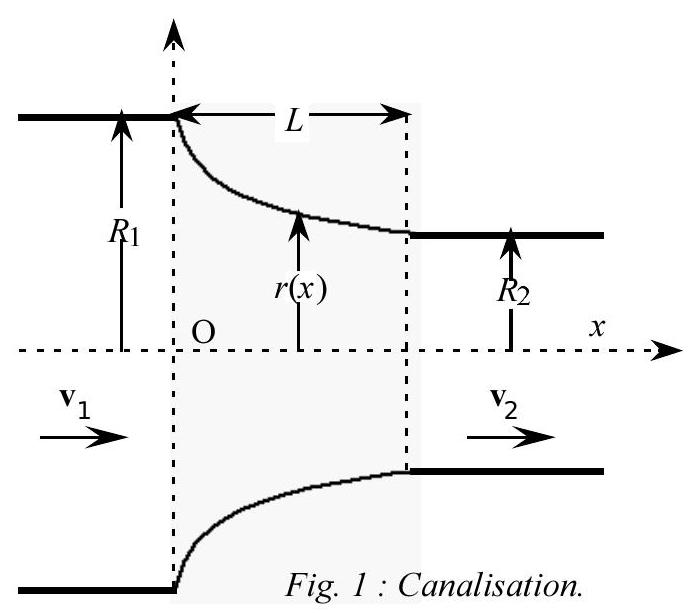
5 - On considère l'écoulement permanent du fluide incompressible à l'intérieur d'une canalisation cylindrique horizontale d'axe
6 - Dans le cas général considéré dans cette question, l'accélération a du fluide est quelconque. Exprimer l'équilibre de l'élément de fluide situé au point
FIN DE CE PROBLÈME
2. Mission pour Mars I: un accident
Un équipage de quatre cosmonautes est chargé de récupérer d'éventuels survivants d'une mission précédente. À l'approche de Mars, le vaisseau spatial rencontre une pluie de micrométéorites. La cabine spatiale est transpercée. La dépressurisation commence, au travers d'un petit trou de section
7 - Avant l'accident, les température et pression dans la cabine spatiale, de volume
la dépressurisation soit très lente. L'air est considéré comme un gaz parfait. En faisant référence à une expérience de thermodynamique, montrer que la température reste constante pendant la dépressurisation.
7 - Avant l'accident, les température et pression dans la cabine spatiale, de volume
la dépressurisation soit très lente. L'air est considéré comme un gaz parfait. En faisant référence à une expérience de thermodynamique, montrer que la température reste constante pendant la dépressurisation.
8 - En négligeant la pesanteur martienne, montrer que la vitesse
9 - Déterminer l'équation différentielle suivie par la pression
FIN DE CE PROBLÈME
3. Mission pour Mars II : nage dans l'espace
Un cosmonaute sort du vaisseau pour apprécier les dégâts. Survient alors l'explosion des
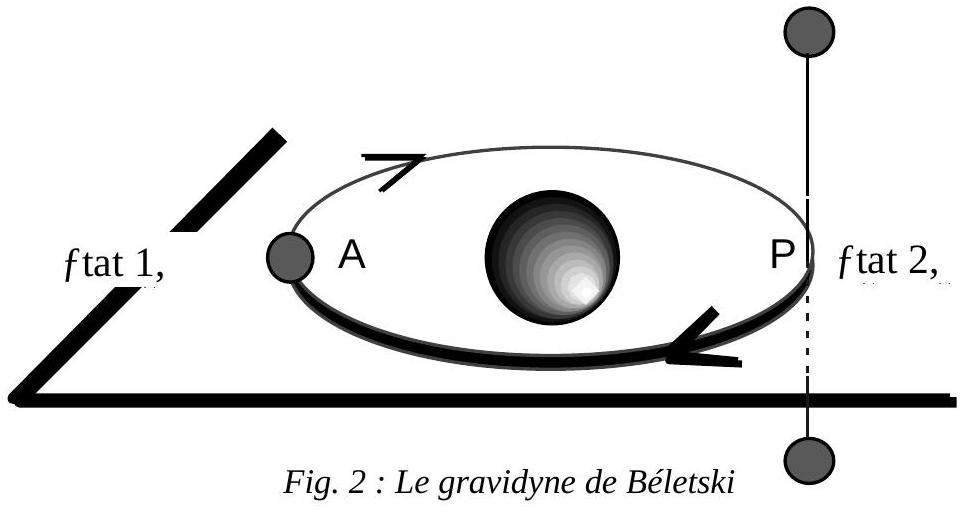
Au temps
moteurs. Le héros se retrouve isolé du reste de l'équipage ; flottant entre le vaisseau et la planète, il est voué à une mort certaine. Pour éviter à ses camarades de prendre des risques inutiles, il enlève son scaphandre...
Il existe pourtant un moyen de changer d'orbite en n'utilisant que la force musculaire, et par transfert résonant d'énergie. Considérons pour le voir le principe du gravidyne, dû au physicien russe Beletski (1977), et modélisé ci-dessous en simplifiant la théorie à l'extrême.
Un vaisseau spatial en orbite circulaire autour d'une planète homogène de masse
où
12 - Lorsque le vaisseau arrive en A, l'équipage débloque la barre, le vaisseau passe à l'état 1. Au regard des ordres de grandeur mis en jeu, on peut admettre que ce passage à l'état 1 se fait à énergie mécanique constante
où
12 - Lorsque le vaisseau arrive en A, l'équipage débloque la barre, le vaisseau passe à l'état 1. Au regard des ordres de grandeur mis en jeu, on peut admettre que ce passage à l'état 1 se fait à énergie mécanique constante
13 - Au point P , l'équipage effectue une nouvelle manœuvre et porte le vaisseau dans l'état 2 ; il débloque la barre au nouvel apogée et ainsi de suite à chaque tour. Au bout de combien de tours,
14 - Selon ce mode de calcul, pour quelle longueur
15 - Montrer que l'énergie dépensée par l'équipage ne dépend que de la masse volumique
16 - Le cosmonaute en péril dans le film se couche dans le plan de son orbite, l'axe de son corps tangent à l'orbite. Il possède deux états: l'état 1 où ses bras sont repliés le long de son corps et l'état 2 où ses bras sont perpendiculaires au plan de l'orbite. Comment doitil s'y prendre pour rejoindre le vaisseau?
16 - Le cosmonaute en péril dans le film se couche dans le plan de son orbite, l'axe de son corps tangent à l'orbite. Il possède deux états: l'état 1 où ses bras sont repliés le long de son corps et l'état 2 où ses bras sont perpendiculaires au plan de l'orbite. Comment doitil s'y prendre pour rejoindre le vaisseau?
17- La masse du cosmonaute est
FIN DE CE PROBLÈME
FIN DE L'ÉPREUVE
Au regard, aussi, du but poursuivi, qui est de s'éloigner de la planète attractrice. Une modélisation plus fine affecterait les trajectoires, mais pas l'effet global.
