J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 2 MP 2011

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2011
Filière
MP
Matière
Physique
Mines MPMines 2011MP PhysiquePhysique 2011
2025_09_04_a2a4f5f3b84864033195g
ÉCOLE DES PONTS PARISTECH SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH, MINES DE SAINT-ÉTIENNE, MINES DE NANCY, TÉLÉCOM BRETAGNE, ENSAE PARISTECH (FILIÈRE MP) ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)
CONCOURS D'ADMISSION 2011
SECONDE ÉPREUVE DE PHYSIQUE

Filière MP

(Durée de l'épreuve: heures)
L'usage de la calculatrice est autorisé

Sujet mis à disposition des concours : Cycle international, ENSTIM, TELECOM INT, TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II - MP.
L'énoncé de cette épreuve comporte 5 pages.
  • Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il est invité à le signaler sur sa copie et à poursuivre sa composition en expliquant les raisons des initiatives qu'il aura été amené à prendre.
  • Il ne faudra pas hésiter à formuler les commentaires (incluant des considérations numériques) qui vous sembleront pertinents, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.

À PROPOS DE CONDUCTION ÉLECTRIQUE

Ce problème étudie deux situations de conduction électrique en présence, entre autres, de champs magnétiques : dans un solide semi-conducteur(partie I) et dans un fluide conducteur (partie II). Ces deux parties sont complètement indépendantes; dans chacune de ces deux parties, de nombreuses questions peuvent aussi être abordées de manière indépendante, sous réserve éventuellement d'admettre certains résultats fournis par l'énoncé.
Les vecteurs sont notés en caractères gras : . Les vecteurs , etc... désignent les vecteurs unitaires selon les axes , etc. . . Un certain nombre de formules d'analyse vectorielle sont rappelées en fin d'énoncé.

I. - Conduction dans un solide semi-conducteur

Les mesures de conductivité et d'effet Hall jouent un rôle important dans l'étude théorique des milieux semi-conducteurs. Ces mesures sont en général menées sur des échantillons plans dont l'épaisseur constante est faible devant les autres longueurs intervenant dans le problème. Le matériau considéré est un conducteur de conductivité , comportant des porteurs de charge mobiles de charge en densité particulaire (nombre de particules par unité de volume) . On notera la constante de Hall du matériau. L'ensemble de l'étude est menée en régime permanent. En l'absence de tout champ magnétique, la loi d'Ohm caractérise le matériau étudié.

I.A. - Mesure directe de la conductivité

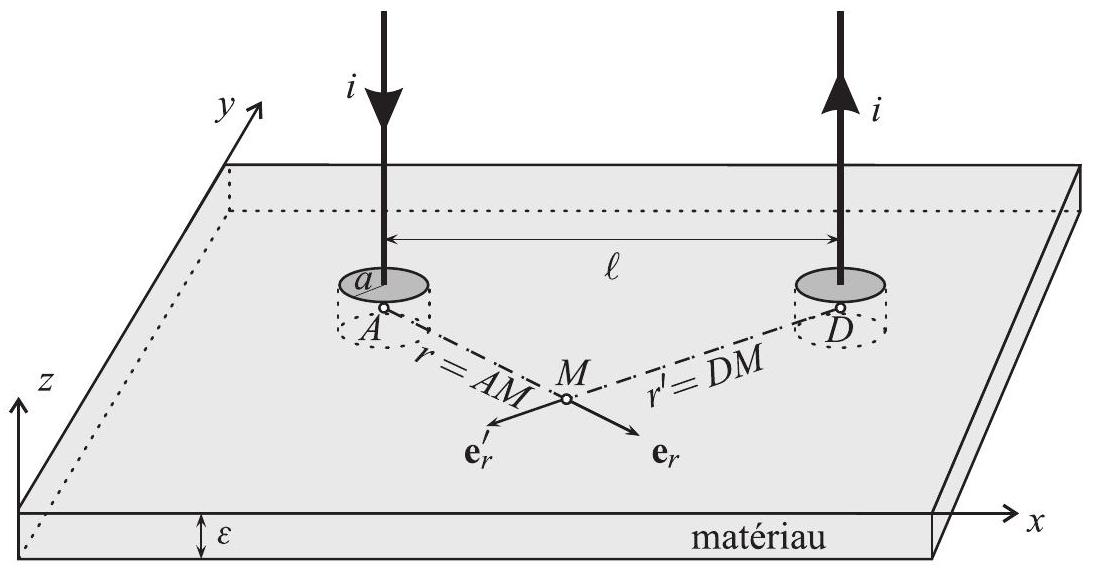
Le courant électrique est amené en un point du matériau par un fil, perpendiculaire à la plaque, confondu avec l'axe . Ce fil est relié au matériau par une électrode cylindrique de faible rayon. Ce courant électrique repart par un fil de même nature et fixé de la même manière au point l'ensemble est représenté sur la figure 1 .
Fig. 1 - Mesure directe de résistance d'une plaque mince conductrice
- On considère tout d'abord une situation simplifiée, à symétrie cylindrique, dans laquelle on supprime le contact de départ en . Le courant arrivant en se répartit donc dans l'ensemble du matériau avec la symétrie de révolution d'axe : la densité volumique de courant en un point s'y écrit , où désigne la distance de à l'axe ( ) et le vecteur unitaire radial de cet axe. Exprimer en fonction de et . On considère deux points et de la plaque et on note et . Déterminer la différence de potentiel en fonction de , et du quotient .
- On remet en place le contact de départ du courant en . En procédant par superposition de deux situations analogues à celle de la question 1 , déterminer la nouvelle expression de en fonction de et . Que vaut cette différence de potentiel si et sont sur la médiatrice du segment ? Commenter ce résultat.
- On note et le rayon des électrodes cylindriques de contact électrique en et ; ces électrodes sont formées d'un matériau métallique très bon conducteur électrique et sont donc considérées comme équipotentielles, de potentiels respectifs et . Montrer que si la résistance électrique de la plaque s'écrit sous la forme , où l'on exprimera en fonction de et .
-4—Application numérique: l'épaisseur de la plaque de semi-conducteur est . On réalise le dispositif de la figure 1 avec et . La conductivité du matériau (silicium dopé) est . Calculer , commenter la valeur numérique ; la mesure de est-elle facile?
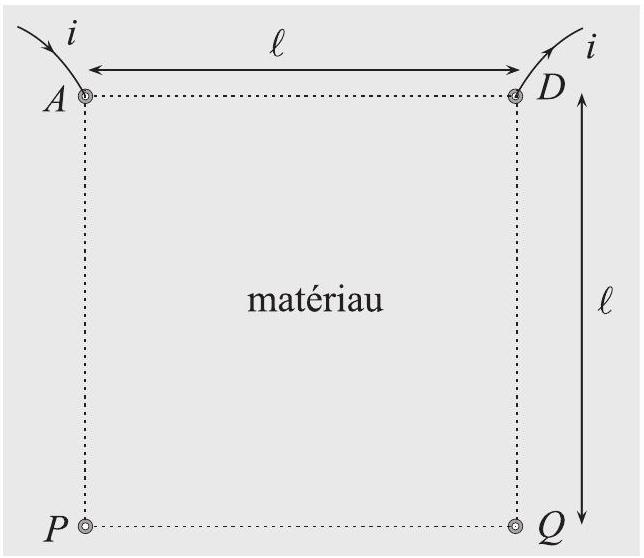
Pour limiter les erreurs dans les mesures de tension on utilise la géométrie de van der Pauw qui élimine l'influence du diamètre des électrodes. Sur la figure 2, les électrodes et sont utilisées pour l'arrivée et le départ du courant, et les électrodes et pour la mesure de
Fig. 2 - Géométrie de van der Pauw : les points et forment dans cet ordre un carré.
différence de potentiel . On définit enfin la résistance parallèle .
- Déterminer en fonction de et .

I.B. - Effet Hall

La plaque infinie de la figure 1 est maintenant soumise au champ magnétostatique uniforme , perpendiculaire à la plaque. Celle-ci étant très mince, le vecteur reste contenu dans le plan formé par la plaque, on a donc et les deux autres composantes de qui ne dépendent que de et . On peut ainsi écrire . Dans le cadre du modèle de Drude, on considère que les porteurs mobiles de charge , de masse et de vitesse associés au courant sont soumis à une force de frottement visqueux de la forme . Certains aspects de cette force seront développés dans la partie II.
  • 6 - En l'absence de tout champ magnétique, écrire l'équation du mouvement d'un porteur de charge associé au courant . Montrer alors qu'en régime permanent, il existe une relation linéaire entre et . Comment s'appelle le coefficient de proportionnalité ?
    - En présence du champ magnétique B que devient l'équation du mouvement? Par analogie avec la question précédente déterminer, en régime permanent, la relation entre et mettant en jeu la conductivité et la constante de Hall .
    On cherche à montrer que la présence du champ magnétique ne modifie pas, compte tenu des conditions aux limites, l'allure des lignes de courant et en particulier que la plaque reste localement neutre, c'est-à-dire que la densité volumique de charge est partout nulle.
    - Déterminer en régime permanent la valeur de .
    - Déterminer, toujours en régime permanent, l'expression de .
    - En utilisant les résultats des questions 7, 8 et 9 ainsi que deux équations de Maxwell montrer qu'en régime permanent la plaque reste en tout point localement neutre.
On considère maintenant la géométrie de la figure 3, on mesure la différence de potentiel et on définit dans cette géométrie la résistance .
- Exprimer la différence de potentiel en fonction de , puis de . En déduire l'expression de la résistance en fonction de et .
- À quoi peut servir dans la pratique une telle mesure
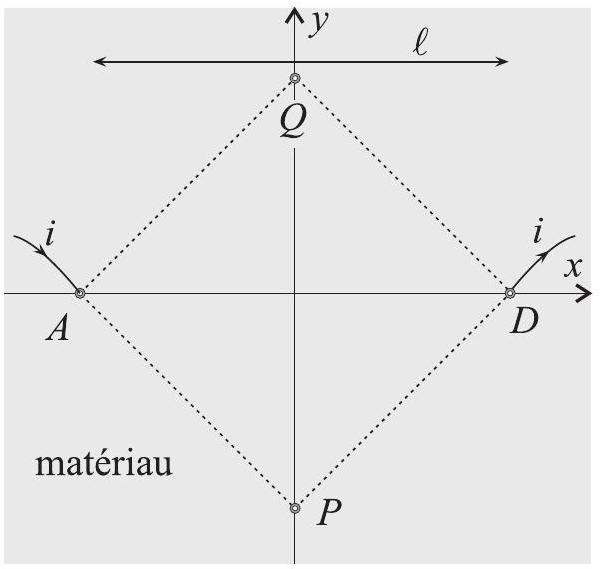
Fig. 3 - Géométrie de van der Pauw : les points et forment dans cet ordre un carré.

FIN DE LA PARTIE I

II. - Conduction dans un plasma à basse fréquence

Le plasma étudié ici est un fluide formé de deux types de particules : des électrons, de masse et de charge , en densité particulaire (nombre de particules par unité de volume) uniforme et des ions, de masse et de charge , en même densité . L'ensemble est soumis au champ électromagnétique en régime variable; on notera, dans le référentiel d'étude, et les vitesses des électrons et des ions en un point donné du plasma. La densité volumique de courant résultant des mouvements des particules est notée . Le plasma étant partout localement neutre, on aura div .

II.A. - Courant électrique dans le plasma

13-Dans quelles conditions peut-on faire l'approximation ? Quel est le nom de cette approximation? On conservera cette approximation dans toute la suite.

II.B. - Vitesses, courant et forces

- Proposer un minorant (numérique) du rapport .
- Quelle est la signification physique de la grandeur définie par ? Exprimer les vitesses et en fonction de , de la densité volumique de courant et de et ; simplifier ces expressions compte tenu du fait que . On conservera cette approximation dans toute la suite.
On considère un élément de volume du plasma dans lequel se trouve ions et autant d'électrons; on cherche à exprimer les forces et respectivement exercées sur ces ions et ces électrons, en négligeant toute force de pression. Les particules ne sont donc soumises qu'aux forces électromagnétiques et aux effets des collisions. Compte-tenu du rapport de masse l'effet des collisions est modélisé uniquement par une force exercée par unité de volume par les ions sur les électrons.
- Exprimer en fonction de et .
- Exprimer en fonction des mêmes grandeurs. En déduire l'expression de , force totale subie par l'élément de volume du plasma. Quel est le nom de cette force?

II.C. - Modèle collisionnel pour le plasma

Pour décrire la force exercée par les ions sur les électrons, on considère une interaction de deux particules de masses et qui, à l'instant initial, se dirigent l'une vers l'autre avec les vitesses et et ; le système est considéré comme isolé et on néglige l'énergie potentielle d'interaction dans l'état initial, les deux particules étant supposées très éloignées l'une de l'autre (cf. fig. 4). Au cours de l'interaction de ces particules, que l'on n'étudiera pas en détail, les vitesses restent toutes colinéaires à l'axe ( ). Au bout d'une durée suffisante, l'interaction est terminée ; les vitesses restent dès lors constamment égales à et , avec et si les deux particules repartent, après l'interaction, en sens inverse de leur mouvement initial.
FIG. 4 - Interaction de deux particules formant un système isolé
18 - En appliquant deux lois de la mécanique au système des deux particules, déduire deux équations reliant et . En déduire la relation .
- En utilisant les diverses expressions obtenues, montrer que , où est la masse réduite du système à deux corps formé par les ions et les électrons. Le facteur numérique que l'on déterminera dans cette expression est lié au modèle géométrique très simple adopté ici : vitesses des particules colinéaires pendant toute l'interaction. Dans un modèle plus complet, on obtiendrai un autre facteur de l'ordre de .
- On revient maintenant au modèle des deux fluides d'électrons et d'ions; on rappelle que désigne la force exercée par unité de volume par les ions sur les électrons du fait des collisions. On note la durée moyenne d'une collision. Justifier, qualitativement, l'expression
  • 21 - Pour les mouvements à suffisamment basse fréquence, on peut négliger l'accélération des électrons dans le plasma. Déduire des questions 16 et 20 la forme généralisée de la loi d'Ohm dans un tel plasma,
où on exprimera en fonction de et .

II.D. - Ondes magnétohydrodynamiques dans un plasma

Le couplage entre le mouvement des particules chargées dans un fluide et le champ électromagnétique régnant dans ce dernier peut, dans certaines conditions, aboutir à la propagation d'ondes dites magnétohydrodynamiques. De telles ondes ont été étudiées pour la première fois par le physicien suédois Hannes Alfvén en 1942, elles sont fondamentales pour l'étude des plasmas astrophysiques tels que ceux qui entourent les étoiles. Pour cette découverte et les découvertes conséquentes, Alfvén obtint le prix Nobel en 1970.
Le plasma étudié ici sera considéré comme très bon conducteur ( donc ) de sorte qu'on peut y écrire (cf. question 21) . Dans ce contexte, l'équation simplifiée de la dynamique dans une unité de volume du plasma s'écrit
On étudie un mode particulier d'oscillations du plasma dans lequel , où est un champ statique intense et une onde de faible amplitude, , qu'on décrira en notation complexe comme une onde plane progressive et monochromatique, où et
- Montrer que . Exprimer, en notation complexe, la densité volumique de courant en fonction de et de la perméabilité du vide .
23 - En se limitant aux termes du premier ordre en , montrer que la vitesse d'ensemble du plasma est aussi une onde plane, où .
  • 24 - En écrivant l'équation de Maxwell-Faraday montrer que les ondes étudiées se propagent sans dispersion à la célérité (vitesse d'Alfvén) que l'on exprimera en fonction de et de la masse volumique du plasma. Vérifier l'homogénéité de la relation donnant .
    - Le plasma étudié est du mercure liquide ( ) dans un champ magnétique . On rappelle que ; calculer ; commenter.

FIN DE LA PARTIE II

Petit formulaire d'analyse vectorielle
En coordonnées cylindriques dans la base locale ( ), pour un champ scalaire et pour un vecteur on indique les relations suivantes :

FIN DE L'ÉPREUVE

Mines Physique 2 MP 2011 - Version Web LaTeX | WikiPrépa | WikiPrépa