J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 2 PSI 2015

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2015
Filière
PSI
Matière
Physique
Mines PSIMines 2015PSI PhysiquePhysique 2015
2025_09_04_88857581b2f583cead49g

ÉCOLE DES PONTS PARISTECH SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH, MINES DE SAINT-ÉTIENNE, MINES DE NANCY, TÉLÉCOM BRETAGNE, ENSAE PARISTECH (FILIÈRE MP) ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)

CONCOURS D'ADMISSION 2015

SECONDE ÉPREUVE DE PHYSIQUE
Filière PSI

(Durée de l'épreuve: 4 heures)L'usage de la calculatrice est autorisé

Sujet mis à disposition des concours : Cycle international, ENSTIM, TELECOM INT, TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II - PSI.
L'énoncé de cette épreuve comporte 7 pages.
  • Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il est invité à le signaler sur sa copie et à poursuivre sa composition en expliquant les raisons des initiatives qu'il aura été amené à prendre.
  • Il ne faudra pas hésiter à formuler les commentaires (incluant des considérations numériques) qui vous sembleront pertinents, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.

MACHINES À ÉCOULEMENT PERMANENT

Ce sujet traite de deux problèmes relatifs à des écoulements permanents de fluides, sous les aspects dynamique et thermodynamique. L'énoncé de cette épreuve comporte donc deux parties I et II, qui sont totalement indépendantes et peuvent être traitées séparément.

I. - Dimensionnement d'une installation de liquéfaction

Dans ce problème, on se propose de dimensionner une installation de production en continu de diazote liquide, fonctionnant en régime permanent (procédé LINDE). Le schéma de principe de l'installation est proposé sur la figure 1. Le problème débute par une description complète de l'installation; les réponses aux questions exigent la prise en compte de l'ensemble des données décrivant l'installation ainsi que du diagramme enthalpique du diazote fourni en annexe.
Du diazote gazeux entre en continu dans la machine avec un débit massique , dans les conditions bar, . Il atteint un mélangeur où on le mélange avec du diazote gazeux de débit dans les mêmes conditions . En sortie du mélangeur ( ), le débit massique de diazote gazeux est donc , toujours dans les conditions ( ).
Après passage par le mélangeur, le diazote traverse une série d'étages de compression; chacun de ces étages est constitué d'un compresseur adiabatique ( ) suivi d'un réfrigérant isobare ( ) à circulation d'eau froide; en sortie du réfrigérant, le diazote gazeux est ramené à une température de sortie égale à .
Les étages compresseur-réfrigérant sont identiques ; ainsi le rapport de compression é est le même pour chacun des compresseurs. Après la traversée du dispositif, le diazote atteint donc le point A à la pression , à la température .
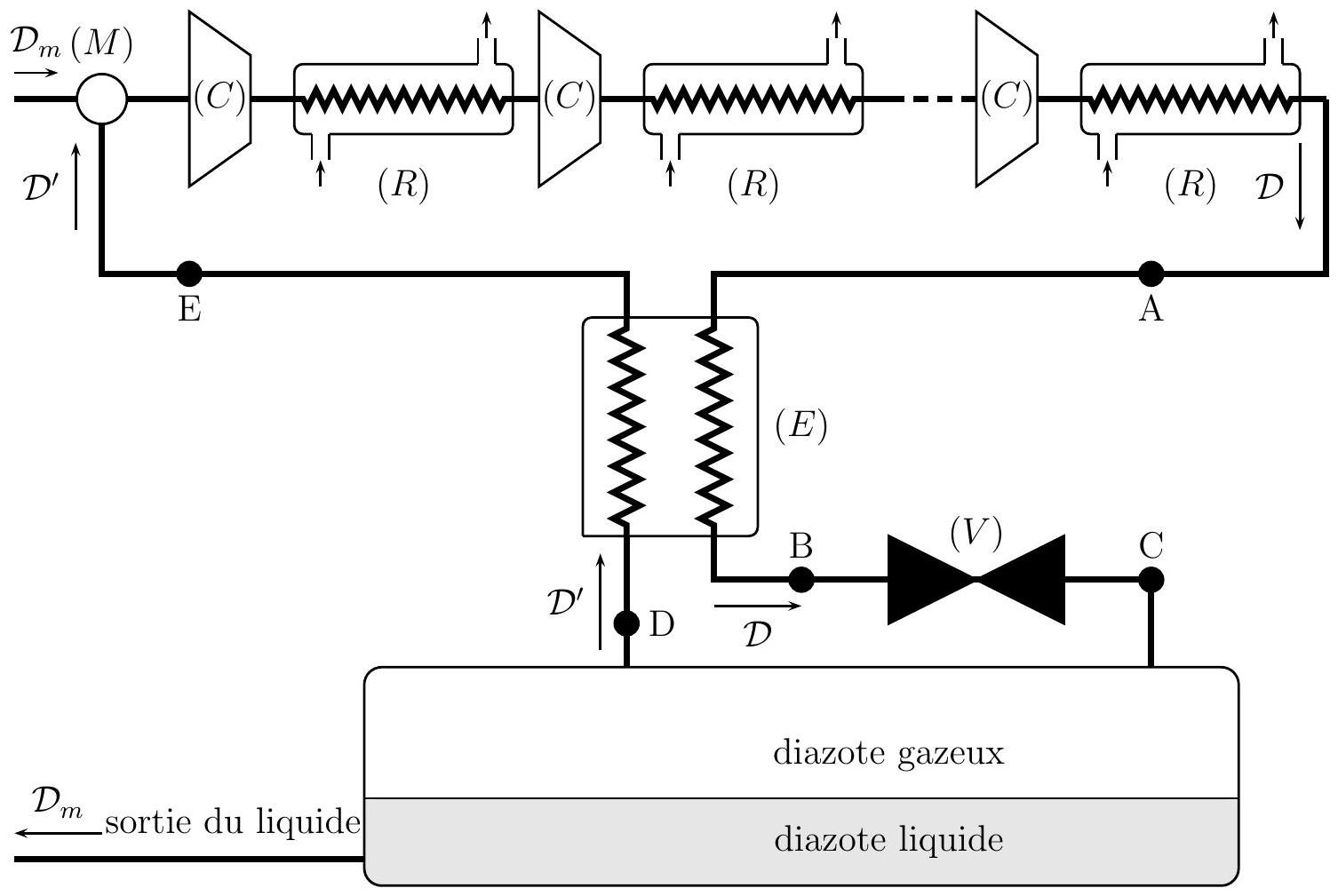
Figure 1 - Schéma de principe d'une installation de liquéfaction de diazote
L'eau liquide utilisée dans chacun des réfrigérants circule à la pression constante de 1 bar; la température de l'eau à l'entrée du dispositif de refroidissement est . On note la capacité thermique massique de l'eau liquide, considérée comme une constante.
Le diazote gazeux aborde entre A et B un échangeur thermique à contre-courant le long duquel il subit un refroidissement isobare; à sa sortie, le fluide est dans l'état bar, . Ce refroidissement est suivi d'une détente isenthalpique dans une vanne de détente ( ).
À la sortie du robinet, le diazote est au point C : c'est un mélange liquide-vapeur dont la fraction massique de liquide est notée , à la pression atmosphérique bar, et à la température é. À cette température, la densité du diazote liquide est .
La fraction massique de diazote liquéfié est faible, on extrait seulement du réservoir un débit massique modeste de diazote liquide dans les conditions ( ); le diazote gazeux recyclé est renvoyé, avec un débit massique , vers l'échangeur ( ). Ce courant du diazote gazeux entre dans ( ) aux conditions bar, .
Dans l'échangeur ( ), le diazote se réchauffe à pression constante et arrive au point E dans les conditions bar, , avant d'être renvoyé vers le mélangeur.
Pour des raisons techniques, on impose deux limites de fonctionnement :
  • la température du diazote ne doit, en aucun point du dispositif, dépasser ;
  • la température de l'eau de refroidissement ne doit pas dépasser en sortie des réfrigérants .
    Le diazote gazeux est diatomique, sa masse molaire vaut . On notera son enthalpie massique en un point K du schéma de la figure 1 .
    La constante molaire des gaz parfaits est .

I.A. - Dimensionnement des étages de compression

Dans cette seule partie I.A le diazote est assimilé à un gaz parfait.
- Que vaut le rapport des capacités thermiques du diazote? On admet que les compresseurs fonctionnent de manière réversible. Déterminer et calculer la valeur minimale de compatible avec les exigences décrites ci-dessus. On adoptera cette valeur dans la suite.
- Si on prenait en compte le caractère irréversible du fonctionnement des compresseurs sans changer la valeur de , faudrait-il augmenter ou diminuer ? On justifiera la réponse.
- On note le débit massique du courant d'eau liquide circulant dans chaque réfrigérant . Déterminer l'expression et calculer la valeur minimale du rapport compatible avec les exigences ci-dessus.

I.B. - Diagramme enthalpique du diazote

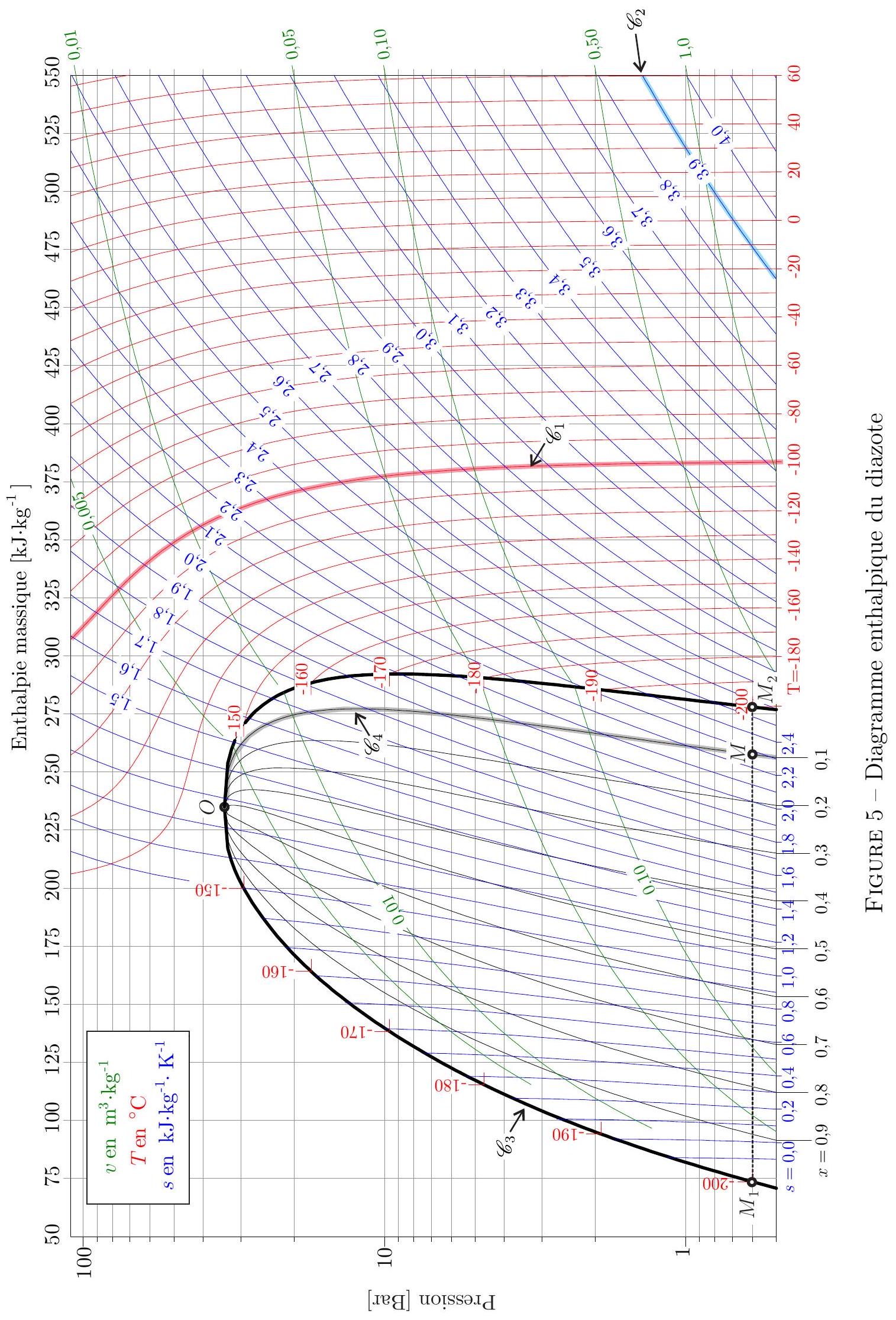
Dans cette partie I.B et la suivante I.C, le diazote n'est plus assimilé à un gaz parfait. La figure 5 fournie en annexe, représente le diagramme enthalpique du diazote sous la forme d'un réseau de courbes.
  • 4 - Identifier la grandeur conservée le long de la courbe . En justifiant votre réponse, déterminer l'asymptote de cette courbe à basse pression.
  • - Identifier la grandeur conservée le long de la courbe . Justifier le sens de variation de cette courbe.
  • 6 - Identifier et nommer les états possibles du diazote sur la courbe .
  • 7 - Identifier la grandeur conservée le long de la courbe . On considère la transformation amenant le diazote de l'état représenté par le point à celui représenté par le point suivant le segment . Décrire l'état du diazote en .

I.C. - Dimensionnement de l'échangeur ( )

- Exprimer en fonction de et des enthalpies massiques du diazote liquide et gazeux, notées et , dans le réservoir.
  • 9 - Le réservoir utilisé en sortie de l'appareil fonctionne aussi en régime permanent; relier et puis et .
10 - Par un bilan que l'on précisera pour le fonctionnement de ( ), déterminer en fonction de et .
  • 11 - En exploitant le diagramme enthalpique du diazote fourni en annexe, déterminer les valeurs de et . Évaluer avec 2 chiffres significatifs. Quelle valeur aurait-on obtenue en considérant que le diazote gazeux vérifie la loi des gaz parfaits?
12- Reproduire sommairement le diagramme enthalpique du diazote en y faisant figurer la courbe et l'isobare à la pression du point B du dispositif. En déduire la valeur de la température et l'état du diazote en ce point.
  • 13 - La production de diazote liquide s'effectue avec un débit . . Dans le cadre du modèle du gaz parfait, évaluer la puissance mécanique qui est nécessaire au fonctionnement de l'ensemble des compresseurs . Comparer votre résultat à la citation suivante, publiée lors de l'exposition universelle de 1900 : Nous avons immédiatement décrit le principe de l'appareil de M. le Dr. Carl Linde; quelques mois plus tard, M. le Dr. d'Ar-

    sonval faisait installer dans son laboratoire du Collège de France une petite machine de 3 chevaux destinée à fournir un litre d'air liquide par heure. L'illustration ci-dessus accompagnait l'article cité.
On notera que ; hp est le symbole de l'unité cheval-vapeur .

FIN DE LA PARTIE I

II. - Roue-vanne de Sagebien

Ce problème décrit le principe d'une roue-vanne utilisée pour les moulins à eau de forte puissance depuis son invention au xix siècle par Alphonse Sagebien.
Rous Sagebier - Dispositions généralis.
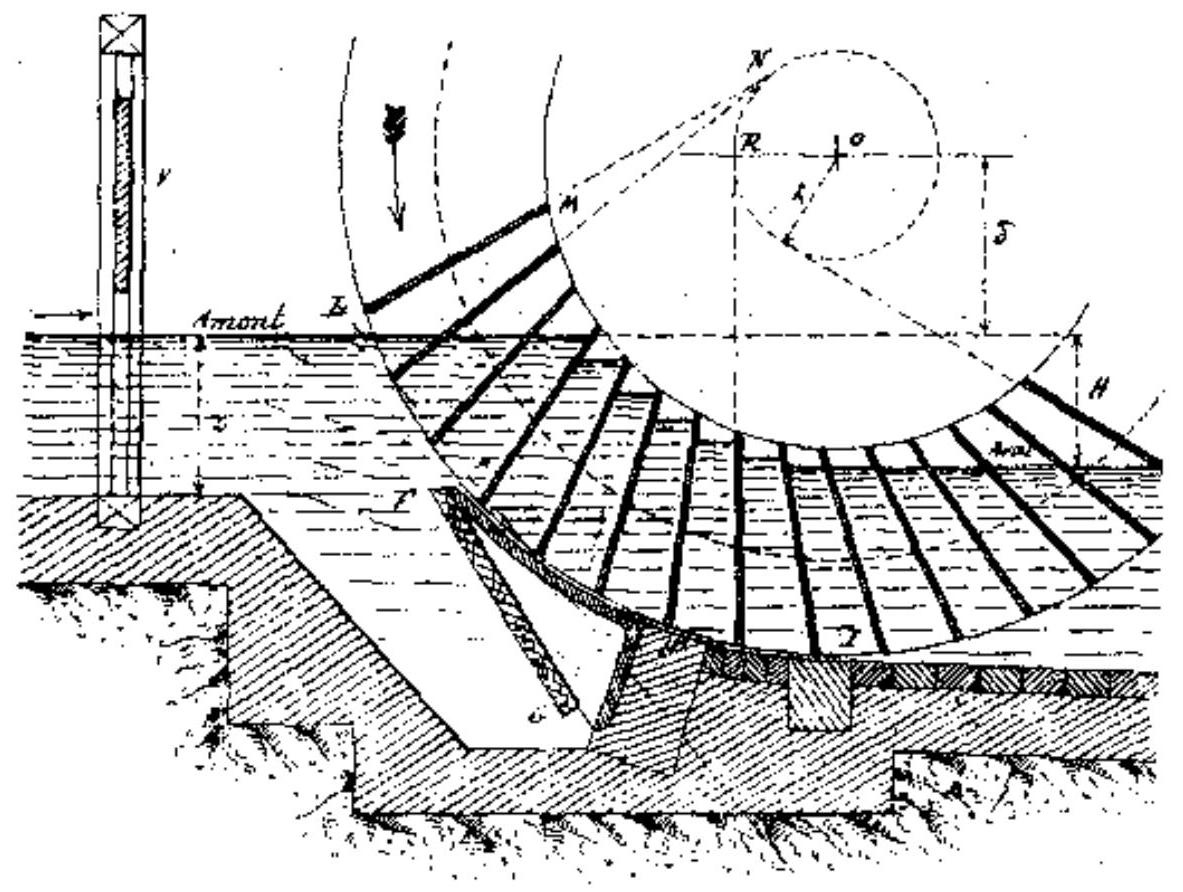
Figure 2 - Schéma historique d'une roue Sagebien
Les roues Sagebien construites à la fin du XIX siècle ont atteint des rendements supérieurs à ceux des meilleures turbines, dépassant régulièrement les . La figure 2 présente un schéma historique de roue-vanne de Sagebien, montrant le dispositif d'obturation du canal d'entrée, permettant l'arrêt de la roue.
La roue-vanne de Sagebien est une roue étroite, à aubes et à rotation lente. L'eau y est amenée par un canal fermé de telle sorte que la roue empêche l'écoulement de l'eau lorsqu'elle ne tourne pas (dans un fonctionnement idéal, sans fuite).
La masse volumique de l'eau vaut ; la pression atmosphérique est bar. Le schéma de principe de la roue-vanne est présenté sur la figure 3 . On notera l'axe (horizontal) de rotation de la roue-vanne.
La vitesse de l'eau dans le canal d'arrivée est égale à celle de l'eau dans le canal de sortie; on notera cette vitesse et sa norme. Le canal d'arrivée (amont) est situé à une hauteur supérieure de à celle du canal de sortie (aval). On choisira un axe vertical ascendant de sorte que l'altitude de la surface du canal d'entrée est . L'accélération de la pesanteur est notée , de norme . On notera la profondeur commune des canaux d'entrée et de sortie.
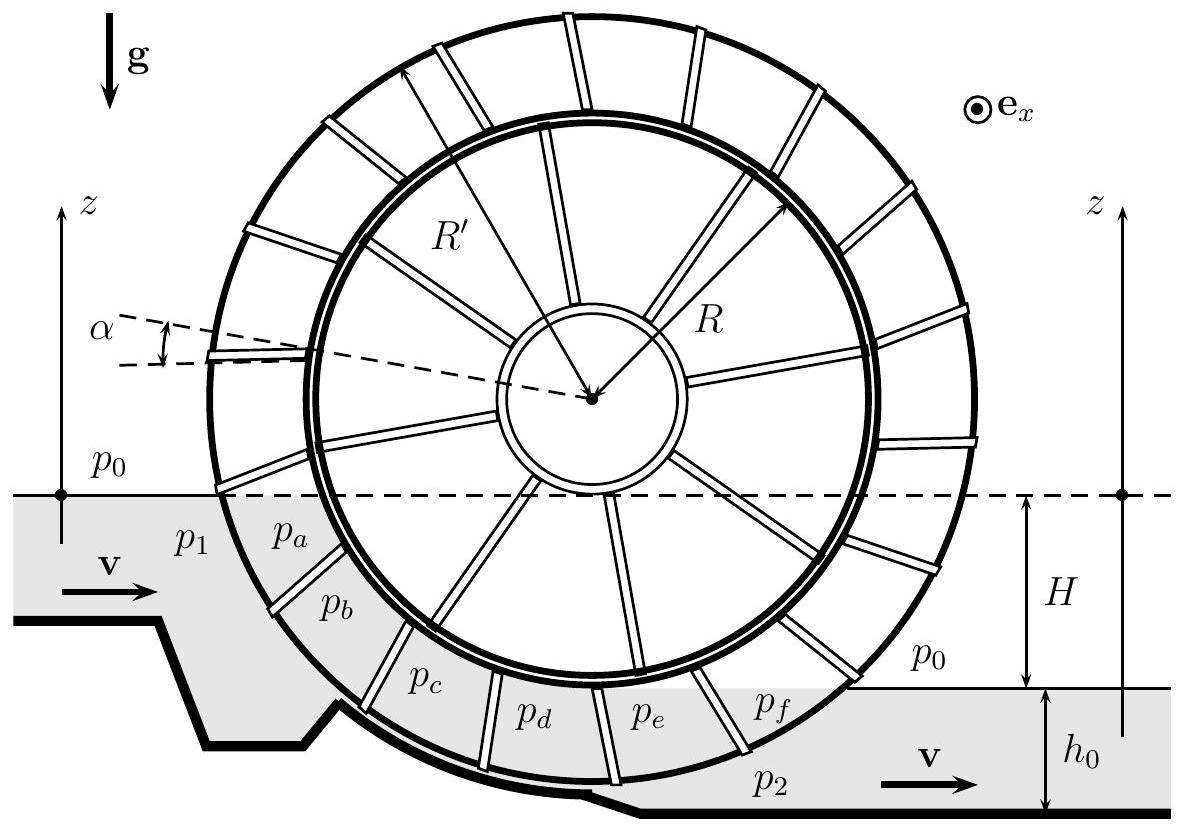
Figure 3 - Roue-vanne de Sagebien
La roue comporte pales rectangulaires, de faible épaisseur, régulièrement disposées entre deux cylindres de rayons et . La largeur de la roue (perpendiculairement au plan de la figure 3) est égale à celle des canaux d'entrée et de sortie; on la notera . Chacune des pales est inclinée d'un faible angle par rapport au rayon de la roue.
Afin d'assurer un fonctionnement sans déperdition d'énergie, on souhaite que la vitesse des diverses pales de la roue en contact avec l'eau soit aussi proche que possible de la vitesse d'amenée et de départ de l'eau.
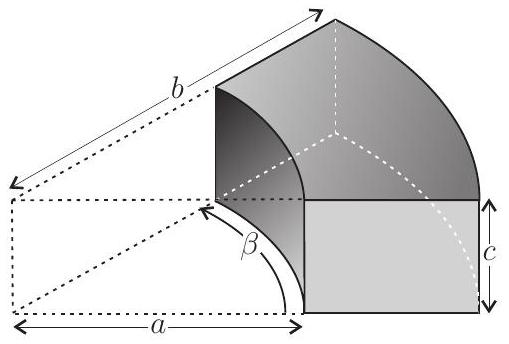
A toutes fins utiles, on précise que le volume de la section d'angle du tore à section rectangulaire représenté en gris sur la figure 4 est donné par la relation .
Figure 4 - Tore à section rectangulaire

II.A. - Étude dynamique du mouvement de la roue-vanne.

  • 14 - Déterminer le débit massique d'eau qui traverse le dispositif. Expliciter la vitesse angulaire de la roue en fonction de et des paramètres géométriques décrivant la roue-vanne.
    - Quelle relation faut-il imposer entre et pour que la vitesse de l'eau soit égale à la vitesse moyenne des points d'une pale de la roue? On se placera dans ce cas dans la suite. Déterminer les valeurs de et si et .
    - Déterminer les relations donnant les champs de pression en amont de la roue et en aval de celle-ci en fonction des données.
Dans un modèle élémentaire, toutes les pales sauf une subissent la même répartition de pression sur les deux faces de la pale, qu'il s'agisse de (pour les pales immergées du côté amont) ou de (pour les pales immergées du côté aval). Ces pales sont dites inactives.
La seule pale active subit sur l'une de ses faces le champ de pression et sur l'autre le champ de pression .
  • 17 - Déterminer la résultante des forces de pression exercées sur une pale inactive. Déterminer la résultante des forces de pression exercées sur la pale active. Déterminer le moment des forces de pression exercées sur l'ensemble de la roue.
  • 18 - Comment ce résultat est-il modifié si les diverses pales séparent la zone d'écoulement en volumes à pression constante et régulièrement décalées : .
  • 19 - Application numérique : on donne et . Déterminer le couple exercé par la roue-vanne sur son axe de rotation.
  • - Déduire de vos connaissances personnelles une évaluation de l'ordre de grandeur du couple moteur nominal développé par une automobile courante, et le comparer à .
    À titre documentaire, on rappelle qu'un cheval-vapeur ou hp vaut .

II.B. - Bilans énergétiques de fonctionnement.

  • 21 - Quelle est la puissance des forces mécaniques exercées sur la roue par l'eau? Commenter l'ordre de grandeur obtenu.
    On considère le système constitué par l'eau contenue entre deux sections droites du canal, l'une située en amont de la roue et l'autre en aval.
  • 22 - Déduire d'un bilan d'énergie appliqué à , l'expression de la puissance fournie par l'eau à la roue.
  • 23 - Définir et calculer le rendement énergétique de la roue. Commenter; préciser en particulier les causes probables, à votre avis, d'une diminution du rendement effectif du dispositif.
Une roue-vanne a été construite par Alphonse Sagebien en 1867 pour l'alimentation de puissance des pompes d'amenée d'eau au canal de l'Ourcq (par prélèvement dans le cours de la Marne). Cette pompe est toujours en état de marche; son rendement pratique est estimé à .

FIN DE LA PARTIE II

Annexe

FIN DE L'ÉPREUVE
Mines Physique 2 PSI 2015 - Version Web LaTeX | WikiPrépa | WikiPrépa