On se contentera de réponses courtes, sauf lorsqu'il est demandé de justifier un résultat donné.
Les applications numériques seront données avec un seul chiffre significatif.
Les parties I, II et III peuvent être résolues de manière indépendante pour l'essentiel.
Ce problème traite de la production d'impulsions lumineuses durant une centaine d'attosecondes ( 1 as

). Ces recherches ont valu aux français Anne L'Huillier et Pierre Agostini de recevoir le prix Nobel de physique en 2023, avec le hongrois Ferenc Krausz. Dans tout ce problème, on notera

, où

est la charge élémentaire (

) et

la permittivité diélectrique du vide.

Dans le cadre du modèle de Bohr de l'atome d'hydrogène, déterminer l'expression de la période de révolution de l'électron dans son niveau fondamental, qu'on notera , en fonction de , de la constante réduite de Planck et de la masse de l'électron .
est la durée caractéristique du mouvement d'un électron dans un atome ou une molécule. Sa valeur numérique, , est inférieure à la femtoseconde ( ). L'étude de ces mouvements est désignée par "science attoseconde" par un léger abus de langage, puisque l'ordre de grandeur est plutôt la centaine d'attosecondes.

I - Production de l'impulsion lumineuse

L'idée générale de la science attoseconde est d'éclairer un échantillon pendant une durée de l'ordre de

. Pour construire cette impulsion lumineuse, la première étape consiste, à partir d'un laser de fréquence

, à créer des harmoniques de fréquences multiples de

, dont la période soit inférieure à

Focalisation d'une impulsion laser

On utilise un laser de longueur d'onde . Dans quel domaine du spectre électromagnétique se trouve-t-il?
Calculer numériquement la période de l'onde émise par le laser, et le rang minimum des harmoniques de période inférieure à .

Détaillons maintenant la méthode permettant de fabriquer ces harmoniques, qui consiste à focaliser une impulsion laser de très haute intensité sur de l'argon. On modélise le champ du laser comme un faisceau gaussien se propageant dans le vide suivant une direction

. On rappelle les formules générales définissant le profil radial d'intensité d'un tel faisceau :

où

désigne la distance à l'axe de propagation,

le waist,

la longueur de Rayleigh, et

le maximum d'intensité.
4. Le faisceau incident a un waist dont la valeur numérique est

. Déterminer l'ordre de grandeur de sa longueur de Rayleigh. Justifier que sur une longueur de l'ordre du mètre au voisinage de

, le faisceau peut être considéré comme étant cylindrique.
5. On focalise ce faisceau cylindrique au moyen d'une lentille mince de focale

, dont le plan est perpendiculaire à la direction de propagation

. L'axe de la lentille et l'axe du faisceau sont identiques. Vérifier que les conditions de l'approximation de Gauss sont satisfaites.
6. On admet que le faisceau émergent est également un faisceau gaussien. Dessiner l'allure de ce faisceau. Exprimer la largeur de son waist, qu'on notera

, en fonction de

. Estimer la valeur numérique de

.
7. Le laser délivre des impulsions d'énergie

pendant une durée

. Déterminer l'ordre de grandeur littéral puis numérique de la puissance par unité de surface au foyer de la lentille, qu'on notera

.
8. Déterminer l'ordre de grandeur littéral de l'amplitude maximale

du champ électrique de l'onde électromagnétique, qu'on exprimera en fonction de

et de la perméabilité magnétique du vide

.
9. Le flux énergétique surfacique que la Terre reçoit du Soleil au-dessus de l'atmosphère est celui d'une onde plane dont l'amplitude du champ électrique vaut

. En déduire, par un argument de proportionnalité, l'ordre de grandeur de

, défini à la question précédente.
10. On note

l'énergie d'ionisation de l'atome d'argon (

). On rappelle que les énergies d'ionisation des atomes sont de l'ordre de 10 eV . Rappeler l'ordre de grandeur de la taille d'un atome. En déduire, par un argument dimensionnel, l'ordre de grandeur du champ électrique vu par un électron périphérique. Comment se compare-t-il au champ

Mouvement d'un électron dans le champ du laser et génération d'harmoniques

On assimile pour simplifier l'atome d'argon à un atome d'hydrogène, comme à la question 1. Lorsque l'atome est éclairé par le laser, l'électron voit le champ électrique du noyau et celui du laser. Pour étudier son mouvement dans la superposition de ces deux champs, nous considérons un modèle classique à une dimension, où l'électron se déplace sur un axe étant la position du noyau, et la direction du champ électrique du laser, , où l'amplitude est supposée uniforme et constante. Exprimer l'énergie potentielle de l'électron, de charge , en fonction de et , et tracer l'allure de sa variation en fonction de .
L'électron est dans un état d'énergie mécanique . Montrer que si dépasse une valeur dite de "saturation" et notée , l'électron échappe à l'attraction du noyau et part à l'infini. Exprimer en fonction de et .
Nommer l'effet quantique qui permet à l'électron de s'échapper, selon une certaine probabilité, même si .
On reprend le modèle unidimensionnel de la question 11, mais avec un champ extérieur qui varie au cours du temps selon . Écrire l'équation du mouvement de l'électron dans la superposition des deux champs, sous la forme d'une équation différentielle pour . On écrira séparément deux équations différentielles suivant que ou .
On s'intéresse au mouvement forcé, défini comme une solution de cette équation qui soit périodique, et de même période que le champ électrique. Sans chercher à déterminer , justifier succinctement que cette solution vérifie aussi .
Dans la décomposition de en série de Fourier, quelles sont les harmoniques compatibles avec cette condition?
On s'intéresse aux trajectoires pour lesquelles l'électron s'échappe de l'atome. On reprend l'équation du mouvement déterminée à la question 14, dans laquelle on néglige désormais le champ du noyau. Déterminer la solution générale de cette équation.
Calculer l'énergie cinétique moyenne de l'électron, notée , en régime sinusoïdal forcé où est périodique. On exprimera en fonction de et .
Intégrer l'équation du mouvement de la question 17 pour un électron partant de l'origine sans vitesse initiale à un temps .
Tracer sur un même graphique l'allure de la variation de en fonction de pour , et , pour variant entre et 1,5 .
La figure 1 donne l'allure de la variation de pour quatre autres valeurs de . On remarque que pour ces valeurs, l'électron revient en à un temps de retour qu'on notera . Écrire l'équation reliant à , sans chercher à la résoudre.

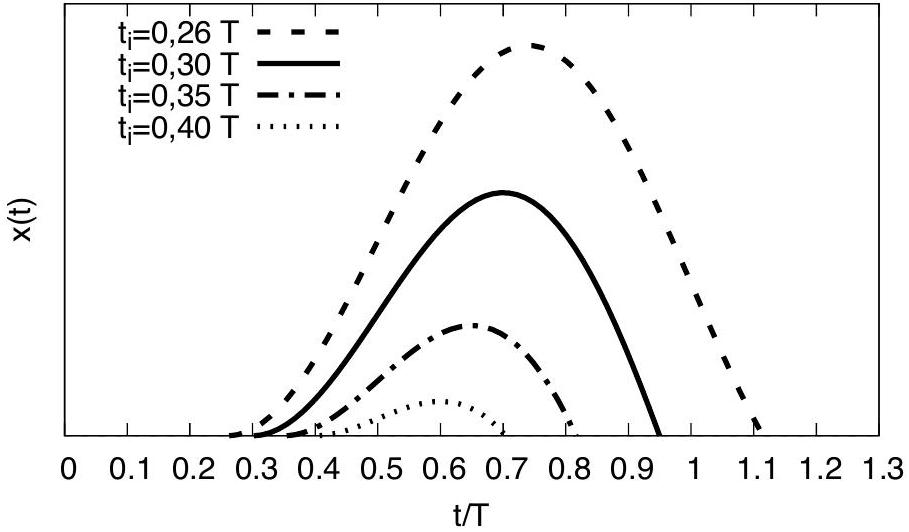
Figure 1 -

Lorsque l'électron revient au point de départ, il peut se recombiner avec le noyau. Ce modèle est connu sous le nom de "modèle en trois étapes" : l'électron est arraché de l'atome, puis fait une excursion dans le champ du laser, puis se recombine avec l'atome. L'énergie libérée dans la recombinaison est la somme de l'énergie d'ionisation, , et de l'énergie cinétique de l'électron à . Cette énergie est rayonnée sous forme d'un unique photon. Exprimer la pulsation de l'onde électromagnétique correspondant à ce photon.
Sur la figure 1, indiquer la courbe pour laquelle l'énergie cinétique est maximale. Quelle est la courbe pour laquelle elle est minimale?
Exprimer en fonction de et .
La figure 2 représente la variation de en fonction de . Recopiez sommairement cette courbe sur votre copie et indiquez les valeurs de en différents points, en vous appuyant sur les résultats précédents.

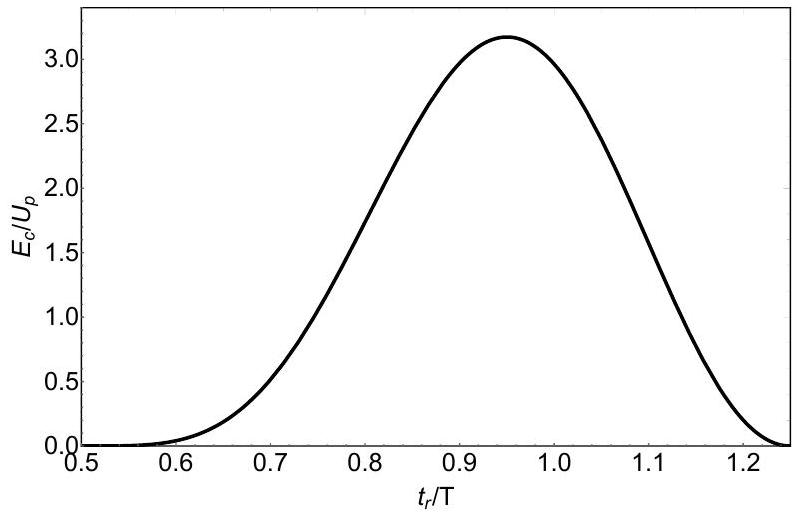
Figure 2 -

La figure 3 représente, sur une échelle des ordonnées logarithmique, la variation de l'intensité de la lumière rayonnée lors de la recombinaison électron-noyau en fonction de la fréquence, cette dernière étant en unité de la fréquence du laser. Comment interprétez-vous l'allure de cette variation? La condition de la question 3 est-elle vérifiée? En utilisant le résultat de la question

22 et la figure 2, donner une expression approximative du rang maximal des harmoniques

en fonction de

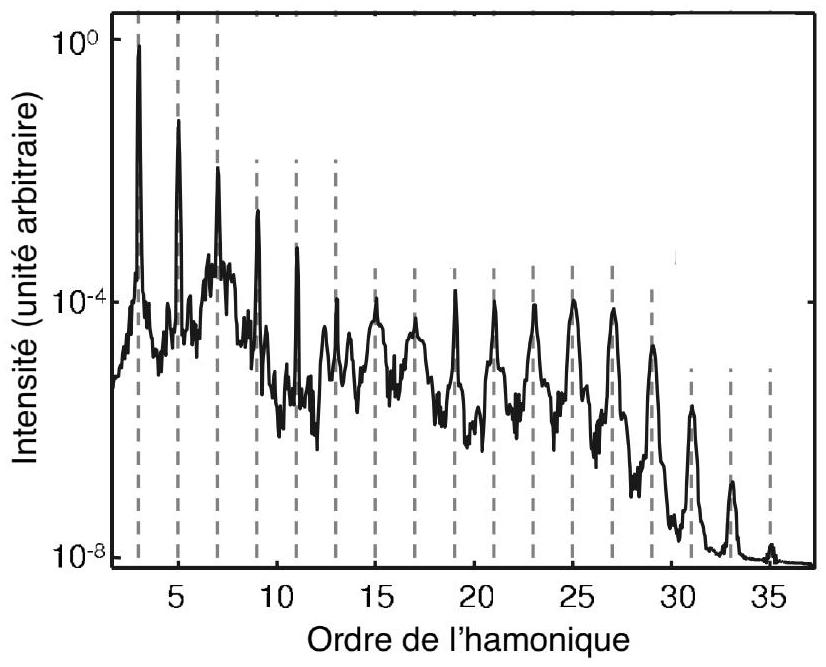
Figure 3 -

II - Mesure de la durée de l'impulsion

La figure 3 montre que le spectre de la lumière émise par l'argon contient un grand nombre de pics d'intensité comparables, associés aux harmoniques du laser incident. Nous allons montrer qu'une telle superposition d'harmoniques peut engendrer une impulsion très brève, puis décrire la méthode expérimentale qui permet de mesurer sa durée.

Largeur du paquet d'ondes

On modélise la lumière émise comme une onde scalaire, qui est une superposition d'harmoniques de pulsations

, où

est un entier strictement positif et

la pulsation du laser. On note

l'amplitude réelle et positive de l'harmonique

, et

sa phase.
27. Exprimer la puissance instantanée

(à une constante multiplicative globale près) en fonction

et des

. Expliquer pourquoi elle ne dépend des phases

qu'à travers leurs différences

.
28. On considère d'abord le cas où l'onde est composée de

harmoniques successives de

, d'amplitude et de phase identique. Montrer que dans le cas

, la puissance instantanée

présente une série de pics étroits identiques espacés de

. Déterminer la demi-largeur des pics en fonction de

.
29. Montrer que la position temporelle des pics de puissance se décale si les

phases

sont en progression arithmétique, les amplitudes

restant identiques.

Mesure des phases relatives

En pratique, on ne mesure pas directement

. On mesure les amplitudes des harmoniques et leurs phases relatives, et on en déduit

par calcul, en utilisant le résultat de la question 27. Nous allons décrire la mesure des phases relatives suivant la méthode nommée RABITT, un acronyme anglais signifiant "reconstruction de battements attosecondes par interférence de transitions à deux photons". Cette méthode utilise une technique dite "pompe-sonde", dans laquelle le faisceau laser est séparé en deux sous-faisceaux dits "pompe" et "sonde", qui suivent deux trajets différents.

La pompe est utilisée pour produire les harmoniques, suivant le dispositif détaillé dans la
première partie. Ces harmoniques se propagent dans la même direction que celle de l'onde émise par le laser pompe, un filtre en aluminium ne laissant passer que celles de rang

suffisamment élevé. Nous appelons "faisceau d'harmoniques" le faisceau obtenu après ce filtrage.
30. Rappeler l'expression de l'énergie

d'un photon dans l'harmonique de rang

Si le faisceau d'harmoniques est focalisé sur un nouvel échantillon d'argon, et si l'énergie

est supérieure à l'énergie d'ionisation

, l'absorption du photon par un atome d'argon conduit, par effet photoélectrique, à l'éjection d'un électron dont l'énergie cinétique vaut

. Dans la méthode RABITT, le faisceau d'harmoniques est mélangé avec le faisceau sonde avant d'être focalisé sur l'argon. L'action combinée des deux faisceaux peut aussi conduire à l'éjection d'un électron d'énergie

, ce qu'on appelle une transition à deux photons.
31. D'après la figure 3 , le faisceau d'harmoniques ne comprend que les harmoniques impaires, et deux pics successifs

ont des amplitudes approximativement égales. En un point donné, l'amplitude du champ électrique associé à ces deux pics est proportionnelle à

. L'amplitude du champ électrique du faisceau sonde est, elle, proportionnelle à

, où

est un retard ajustable. On admet que l'amplitude de probabilité du processus quantique de transition à deux photons est proportionnelle au produit de ces amplitudes,

. En utilisant une représentation complexe, isoler dans ce produit les composantes proportionnelles à

, correspondant à l'éjection d'un électron d'énergie

.
32. Exprimer la probabilité correspondante, et tracer sa variation en fonction de

. Pourquoi parle-t-on d'interférence de transitions à deux photons? Exprimer l'intervalle entre deux maximums de probabilité.

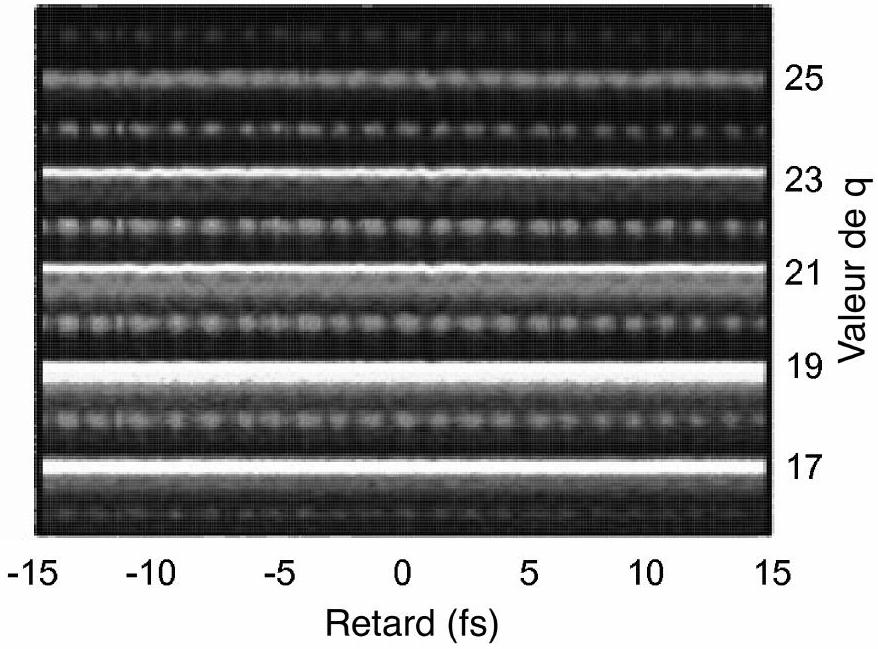
Figure 4 - Nombre de photoélectrons d'énergie

en fonction du retard

et de

, les zones les plus claires correspondant aux plus grands nombres [extrait de l'article "Physics of attosecond pulses produced via high harmonic generation", par Katalin Varjù, Per Johnsson, Johan Mauritsson, Anne L'Huillier, Rodrigo López-Martens, Am. J. Phys. 77, 389-395 (2009)].

La mesure de l'énergie cinétique de l'électron donne accès à la valeur de (voir la fin du problème). La figure 4 représente le nombre d'électrons émis en fonction de et . Commenter cette figure à la lueur de la figure 3 et des deux dernières questions, en distinguant les valeurs de paires et impaires. Vérifier que la valeur de déduite de cette figure est compatible avec celle obtenue à la question 3.
Comment, sur la figure 4 , peut-on vérifier si est indépendant de ?
Dans ce cas, donner une estimation de la durée de l'impulsion du faisceau d'harmoniques.

III - Spectromètre magnétique

La mesure de l'énergie cinétique des électrons est réalisée par un spectromètre magnétique dont nous décrivons le principe.
36. On considère d'abord le mouvement d'un électron dans un champ magnétique

uniforme, la vitesse initiale de l'électron étant orthogonale à

. Déterminer le rayon

de la trajectoire en fonction de

, et de la vitesse, notée

.
37. En déduire la valeur absolue du moment cinétique

de l'électron par rapport au centre de la trajectoire, qu'on exprimera en fonction de

.
38. On considère maintenant le cas d'une vitesse initiale

quelconque. On note

l'angle entre

. Le mouvement dans un plan perpendiculaire au champ est toujours un cercle. Exprimer son rayon

en fonction de

Le spectromètre utilise un champ magnétique constant, non uniforme, mais possédant une symétrie de révolution. Le champ en un point

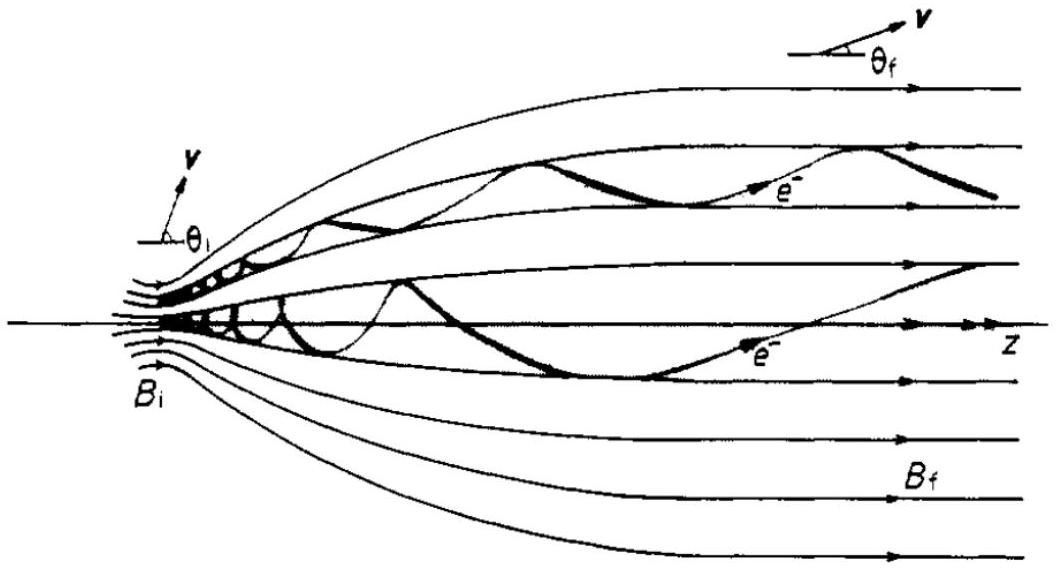
est contenu dans le plan contenant l'axe

. Cette configuration est représentée sur la figure 5. Les électrons entrent par la gauche, puis parcourent une longue distance où le champ est quasiment uniforme, et sont détectés à droite.

Figure 5 - Lignes de champ et trajectoires des électrons (projetées sur le plan de la figure).

Indiquer comment varie la norme du champ magnétique de gauche à droite le long d'une ligne de champ.
Lorsque le champ vu par l'électron varie lentement le long de sa trajectoire, son mouvement dans le plan perpendiculaire reste approximativement circulaire, mais avec un rayon qui varie peu à peu. On admet que la variation de ce rayon est telle que le moment cinétique déterminé à la question 37 reste constant. On considère pour simplifier que le champ est uniforme sur chacune des surfaces d'entrée et de sortie du spectromètre, et on note et les normes correspondantes. Déterminer la relation entre l'inclinaison initiale et finale de la trajectoire.
Les électrons produits par l'effet photoélectrique ont des directions aléatoires. Le but est de recueillir tous ceux qui entrent dans le spectromètre, et d'aligner rapidement leur trajectoires avec l'axe . On choisit donc des valeurs de et telles que soit petit, et on fabrique un spectromètre suffisamment long pour que la plus grande partie de la trajectoire se fasse dans un champ uniforme . On mesure le temps séparant l'impulsion laser, qui produit les électrons, et leur détection à la sortie du spectromètre. Connaissant la longueur du spectromètre, on en déduit leur vitesse, et donc leur énergie cinétique. Du fait de l'inclinaison non nulle, la longueur parcourue par les électrons n'est pas exactement . En déduire l'incertitude relative sur la vitesse en fonction du rapport .