J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

X ENS Physique MP 2016

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo x-ens
🔗 Explorer
Banque
X-ENS
Année
2016
Filière
MP
Matière
Physique
X-ENS MPX-ENS 2016MP PhysiquePhysique 2016
2025_09_04_3fa7174bb7cd007a8550g

ÉCOLE POLYTECHNIQUE - ÉCOLES NORMALES SUPÉRIEURES

COMPOSITION DE PHYSIQUE (XULCR)

(Durée : 4 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Les résultats des applications numériques seront donnés avec un chiffre significatif.

Optomécanique en cavité

L'optomécanique se consacre à l'étude du couplage de dispositifs mécaniques à une onde électromagnétique. Ce problème étudie différents aspects d'un système optomécanique modèle, à savoir une cavité résonante linéaire formée de deux miroirs semi-réfléchissants parallèles se faisant face, dont l'un est mobile.
Dans la première partie, on établit les équations dynamiques générales d'une cavité de longueur fixée, soumise à un champ électromagnétique incident. Dans la seconde partie, on étudie le couplage optomécanique en supposant que l'un des miroirs est libre de se déplacer sous l'action de la force d'origine électromagnétique imposée par le faisceau incident, et d'une force de rappel élastique appliquée par le support sur lequel ce miroir est monté.
Dans tout ce problème, on utilise le signe " " (plutôt que " ") pour définir une grandeur.
Dans les applications numériques, on prendra pour la vitesse de la lumière dans le vide, et .

1. Cavité résonante de longueur fixée

On considère une cavité linéaire, d'axe , délimitée par deux miroirs (diélectriques) semi-réfléchissants plans identiques, notés et . On admettra que les faces «internes» des miroirs et - c'est-à-dire les faces dirigées vers l'intérieur de la cavité (représentées en trait plein sur la figure 1), ont même coefficient de réflexion en amplitude (pour le champ électrique) pris égal à ( ), où est supposé réel et positif; le coefficient de réflexion des faces «externes» de et - c'est-à-dire les faces dirigées vers l'extérieur de la cavité (représentées par les zones grisées sur la figure 1), est quant à lui pris égal à . On admettra aussi que les deux miroirs ( ) et ( ) possèdent le même coefficient de transmission en amplitude (pour le champ électrique), noté , que l'on suppose réel et positif; ce coefficient est identique pour les deux sens de traversée des miroirs. On admettra enfin que les coefficients ( ) ne dépendent pas de la pulsation du champ incident, et que la relation est vérifiée. On note et . Dans cette partie, on suppose les deux miroirs fixes dans le référentiel du laboratoire et l'on note la distance qui sépare ( ) et ( ).
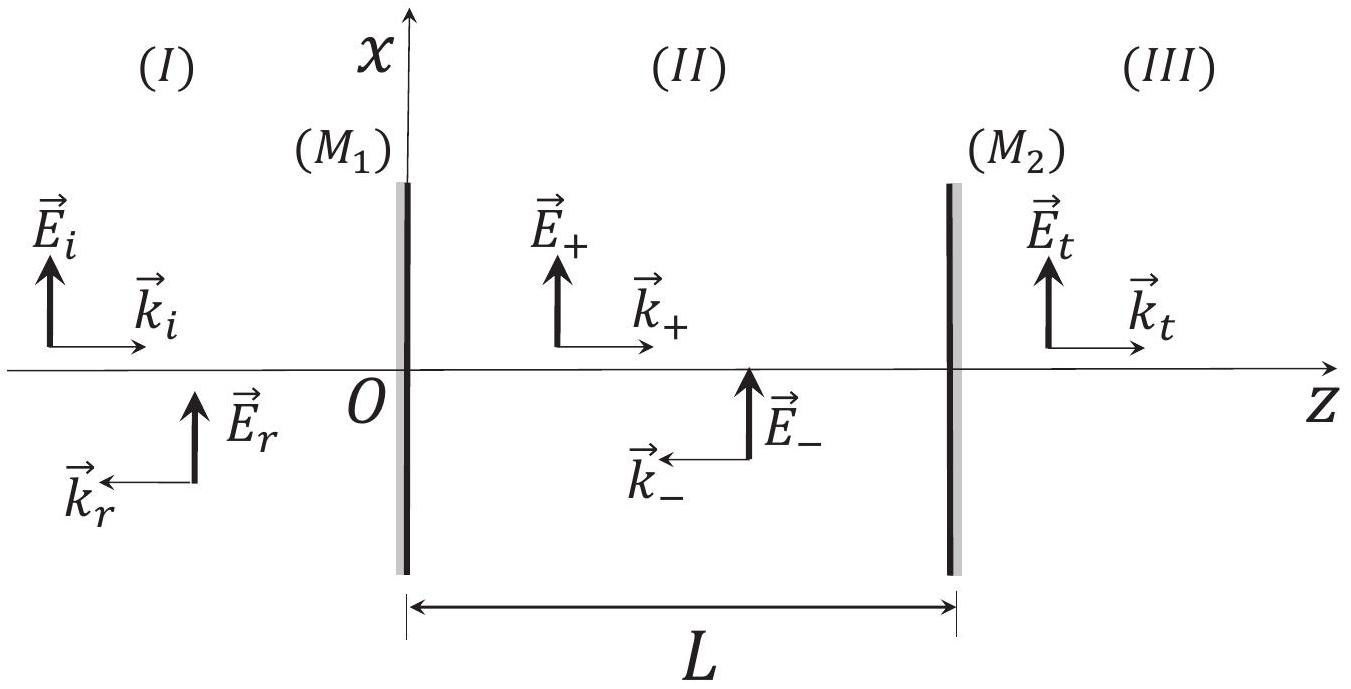
On envoie vers la cavité formée par ( ) et ( ) une onde incidente plane progressive monochromatique se propageant selon l'axe ( ) et polarisée selon l'axe ( ), décrite par son champ électrique :
Figure 1 - Cavité résonante linéaire de longueur , soumise à un champ incident (partie 1).
où désigne la partie réelle, l'amplitude de l'onde incidente à l'origine des temps et des coordonnées, supposée réelle, et . Vous admettrez que cette onde crée une onde réfléchie dans le demi-espace de même direction de polarisation que l'onde incidente, de sorte que le champ total en amont de la cavité (dans la zone notée I sur la figure 1) s'écrit
où désigne l'amplitude de l'onde réfléchie à l'origine des temps et des coordonnées, a priori complexe.
De même, le champ créé à l'intérieur de la cavité (zone II) prend la forme générale
Enfin, le champ au-delà de la cavité (zone III) s'écrit
Ces différents champs sont représentés sur la figure 1 ainsi que les vecteurs d'ondes associés
  1. Que représentent les coefficients et ? Que signifie physiquement la relation ?
  2. Justifiez la nature progressive choisie pour le champ .
  3. Au moyen des coefficients de réflexion et transmission, écrivez trois relations entre les amplitudes et traduisant la transmission/réflexion en et .
  4. Déduisez les amplitudes et en fonction de et . Vous mettrez le résultat sous la forme
et vérifierez que la fonction prend la forme
  1. Exprimez la fonction et tracez sa représentation graphique pour en fonction de la variable réduite .
  2. Montrez l'existence d'une famille discrète de pulsations du champ incident pour lesquelles est maximale. À quoi ces pulsations correspondent-elles physiquement pour l'intensité transmise ?
  3. Montrez que l'intensité (moyennée sur une période) à l'intérieur de la cavité se met sous la forme où désigne l'intensité incidente et un terme que vous exprimerez en fonction de et .
  4. Tracez les courbes représentatives de pour et et 3 en fonction de la variable réduite . Même question pour ; quelle est la nature de l'onde observée à l'intérieur de la cavité dans ce cas?
  5. On revient au cas général ( ). En vous plaçant au voisinage d'une pulsation déterminez une expression approchée de la fonction puis mettez la fonction sous la forme
où est un paramètre dont vous préciserez l'expression et la signification physique. Donnez l'expression approchée de dans la limite .
10) En vous servant des résultats précédents, établissez une analogie entre la cavité étudiée et des dispositifs rencontrés dans un (d') autre(s) domaine(s) de la physique. À partir de cette analogie, définissez un facteur de qualité pour la cavité considérée et indiquez sa signification physique.
Dans les questions 11 à 15 , on cherche à relier le paramètre au taux de perte en énergie de la cavité. Pour ce faire, on va suivre une approche particulaire. On rappelle qu'une onde électromagnétique est composée de photons, particules sans masse, dont la quantité de mouvement et l'énergie sont données par les formules et , où est la pulsation du rayonnement électromagnétique considéré. On admet que, lorsqu'il atteint l'un des miroirs ( ) ou ( ), un photon est transmis, sans modification de son énergie ni de sa quantité de mouvement, avec la probabilité , tandis qu'il «rebondit», sans modification de son énergie mais avec une quantité de mouvement opposée, avec la probabilité .
11) Exprimez le temps mis par un photon pour parcourir une longueur de cavité.
12) Durant cet intervalle de temps, combien un photon subit-il de rebonds sur les parois de la cavité ?
13) Quelle est la probabilité pour ce photon de quitter la cavité pendant la durée ?
14) Si la cavité contient, à l'instant photons, combien de photons auront quitté la cavité à l'instant (on suppose )?
15) Reliez l'énergie électromagnétique contenue dans la cavité au nombre de photons . En supposant , exprimez la variation d'énergie électromagnétique ( ) pertes entre et due aux pertes au niveau des miroirs. En assimilant et à des éléments infinitésimaux exprimez le taux de perte de la cavité . Finalement, reliez au paramètre introduit à la question 9 .
On suppose maintenant que les champs sont quasi-monochromatiques, c'est-à-dire qu'ils peuvent se mettre sous la forme de paquets d'ondes
où les fonctions et ne prennent de valeurs significatives que sur l'intervalle autour d'une pulsation où et .
16) Rappelez brièvement pourquoi un paquet d'ondes de la forme précédente constitue une solution des équations de Maxwell.
17) En utilisant la forme approchée pour obtenue à la question 9 , établissez la relation linéaire entre les composantes et dans le régime .
18) Déduisez du résultat précédent l'équation différentielle vérifiée par la fonction
  1. On considère une cavité de longueur , constituée de deux miroirs de même coefficient . Calculez ainsi que la longueur d'onde associée . À quel type d'onde électromagnétique a-t-on affaire? Calculez ainsi que le facteur de qualité . Commenter la comparaison aux ordres de grandeur caractéristiques rencontrés dans d'autres domaines de la physique.

2. Cavité résonante à miroir mobile

Dans cette partie, on suppose que le miroir ( ) est libre de se déplacer selon la direction . Il est soumis à la force imposée par le champ électromagnétique à l'intérieur de la cavité ainsi qu'à une force de rappel élastique linéaire modélisée par un ressort de raideur et de masse négligeable devant celle du miroir ( ) qu'on notera . Expérimentalement, cette configuration peut être réalisée en suspendant le miroir comme un pendule. On repère la position de ( ) par son écart, noté , à sa position d'équilibre à champ incident nul, correspondant à une longueur de cavité (cf Figure 2). On supposera que le mouvement de ( ) reste de faible amplitude devant la longueur initiale de la cavité.
20) Exprimez la longueur de la cavité à la date .
21) Donnez la nouvelle expression de la pulsation introduite dans la première partie. Calculez sa forme approchée au premier ordre en . Vous ferez intervenir les grandeurs et (appelée «constante de couplage électromécanique » ).
22) À quelle condition (intuitive) l'équation dynamique (19) reste-t-elle valable ? Pour répondre à cette question, vous pourrez introduire l'échelle des variations temporelles de la fonction .
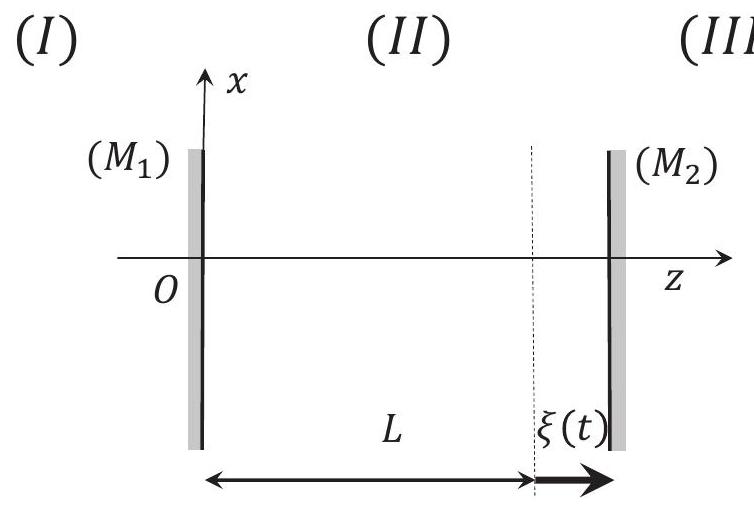
Figure 2 - Cavité résonante à miroir mobile (partie 2).
On suppose que le champ incident est monochromatique, de pulsation ,
où est une constante réelle, et l'on écrit la composante du champ à l'intérieur de la cavité sous la forme
  1. Pourquoi suppose-t-on, a priori, que dépend du temps? Justifiez qualitativement que ne varie pas de manière significative sur une période du champ incident.
  2. Montrez que vérifie
Dans les questions 25 à 34 , on souhaite déterminer l'expression de la force imposée au miroir ( ) par le champ électromagnétique en cavité, appelée «force de pression de radiation», en fonction des paramètres du problème et notamment du déplacement . Pour ce faire, on va suivre le même type d'approche particulaire que dans les questions 11 à 15.
25) Exprimez la quantité de mouvement fournie au miroir ( ) par un photon de pulsation lors d'un rebond. Comme dans la première partie, on supposera que ce rebond ne modifie pas l'énergie du photon de manière significative mais change sa quantité de mouvement en son opposée.
26) En notant le nombre de photons qui frappent le miroir ( ) entre et , donnez l'expression de la force de pression de radiation due au champ à l'intérieur de la cavité.
27) Reliez à la puissance électromagnétique, moyennée sur une période du champ incident, qui est réfléchie par le miroir ( ) à l'instant .
28) Montrez que, dans la limite , la force de pression de radiation instantanée prend alors la forme
On introduit les nouvelles grandeurs et définies par
  1. Précisez les dimensions respectives de et et explicitez la signification physique des quantités et .
  2. Établissez l'équation régissant l'évolution de .
  3. Établissez l'équation mécanique sur régissant le mouvement du miroir. Vous introduirez la pulsation propre de l'oscillateur que vous relierez à la raideur du ressort et la masse de ( ).
  4. On se propose d'étudier le système dans le cas . Que signifie cette condition physiquement?
  5. Montrez que, pour des temps , on peut alors écrire
  1. Dans le régime considéré à la question précédente, établissez l'expression de la force de pression de radiation.
Dans la suite du problème, on supposera toujours être dans les conditions d'application de la formule (26).
Le but des questions 35 à 40 est d'étudier les positions d'équilibre mécanique du miroir mobile ( ), ainsi que leur stabilité.
35) Établissez la condition d'équilibre mécanique du miroir mobile ( ) reliant à .
36) En l'absence de champ incident, déterminez le nombre et la nature (stable ou instable) de points d'équilibre du miroir mobile .
On considère maintenant le cas d'un champ incident non nul.
37) Mettez la condition d'équilibre identifiée à la question 35 sous la forme , où est une fonction sans dimension de maximum unité et une constante qui s'exprime en fonction des paramètres du problème, puis montrez comment déterminer graphiquement le(s) point(s) d'équilibre du miroir ( ).
38) À l'aide de la représentation graphique de la question précédente, montrez que le miroir ( ) possède au plus trois points d'équilibre et étudiez leur stabilité respective. Justifiez le nom de bistabilité donné au phénomène observé.
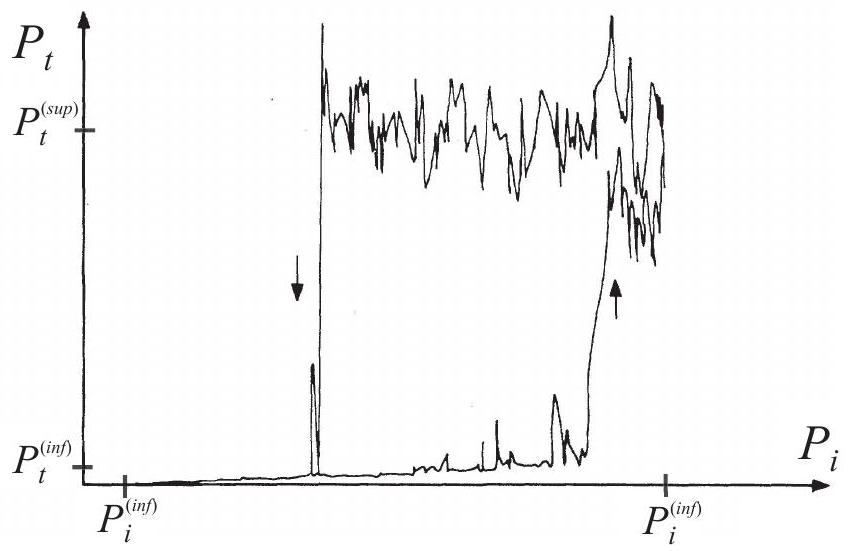
Figure 3 - Relevé expérimental de la puissance (représentée en ordonnée) transmise par une cavité ( ) obtenu en faisant passer très lentement la puissance du champ incident (représentée en abscisse) de à et inversement. Lors du passage , on suit la partie inférieure du cycle d'hystérésis (le niveau moyen du plateau inférieur est ); au cours du passage , on suit la partie supérieure du cycle (le niveau moyen du plateau supérieur est ). La figure est extraite de A. Dorsel et al, Phys. Rev. Lett. 51, 1550 (1983).
  1. À partir de la condition d'équilibre de la question 35 , montrez qu'il est nécessaire de choisir pour obtenir plus d'un point d'équilibre pour le miroir .
  2. En supposant , identifiez l'intervalle dans lequel doit se situer pour qu'il existe plus d'un point d'équilibre pour le miroir mobile ( ).
Dans les questions suivantes, on considère une cavité de longueur initiale , constituée d'un miroir massif (immobile) et d'un miroir mobile de masse 60 mg , tous deux possédant le même coefficient . La figure 3 présente un relevé expérimental de la puissance transmise par la cavité, notée et représentée en ordonnée, obtenu lorsque l'on fait passer très lentement la puissance incidente (représentée en abscisse) de la valeur inférieure vers la valeur supérieure , puis inversement. La courbe obtenue, appelée cycle d'hystérésis, présente deux branches dont le sens de parcours est indiqué par des flèches : durant la première phase, c'est-à-dire lorsque l'on augmente de à , on suit la partie inférieure du cycle; au cours de la deuxième phase, c'est-à-dire lorsque l'on diminue de à , on suit la partie supérieure du cycle.
41) Établissez la relation entre puissances transmise et incidente faisant intervenir la quantité .
42) En vous appuyant sur les résultats des questions 37 et 38 , donnez une interprétation qualitative des résultats obtenus. Expliquez notamment l'existence de deux plateaux pour la puissance transmise et le «passage» de l'un à l'autre de ces plateaux. Vous pourrez vous aider de représentations graphiques de votre choix pour illustrer votre réponse.
X ENS Physique MP 2016 - Version Web LaTeX | WikiPrépa | WikiPrépa