Version interactive avec LaTeX compilé
ECOLE POLYTECHNIQUE ECOLES NORMALES SUPERIEURES
CONCOURS D'ADMISSION 2025
MERCREDI 16 AVRIL 2025 08h00-12h00
FILIERE MPI - Epreuve n
PHYSIQUE MPI (XUL)
Durée: 4 heures
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve
Ondes électromagnétiques à la surface des plasmas
On se contentera de réponses courtes, sauf à la question 29 où on détaillera le calcul. Les parties I et II sont largement indépendantes.
Dans de nombreuses situations, les électrons de conduction d'un métal peuvent être modélisés comme les électrons d'un plasma dilué. Ils présentent des modes d'oscillation, qu'on désigne sous le terme générique de plasmons. Ce problème étudie deux catégories de plasmons : ceux qui apparaissent dans des petites billes ou tiges métalliques de taille nanométrique, dits plasmons de surface localisés, et ceux qu'on observe au voisinage de la surface plane d'un métal de grande dimension, dits simplement plasmons de surface. Ces plasmons ont de nombreuses applications tirant parti du fait qu'ils absorbent la lumière à des fréquences précises.
Dans tout ce problème, on modélise le métal comme un plasma dilué. On note
I - Plasmons de surface localisés
- On considère une plaque de métal d'épaisseur négligeable par rapport à ses dimensions transversales. Elle porte sur une face une densité de charges surfacique uniforme
, et sur l'autre une densité (figure ). On suppose dans toute cette partie que le métal est placé dans le vide. En appliquant les lois de l'électrostatique, déterminer le champ électrique à l'intérieur et à l'extérieur de la plaque en un point éloigné du bord.
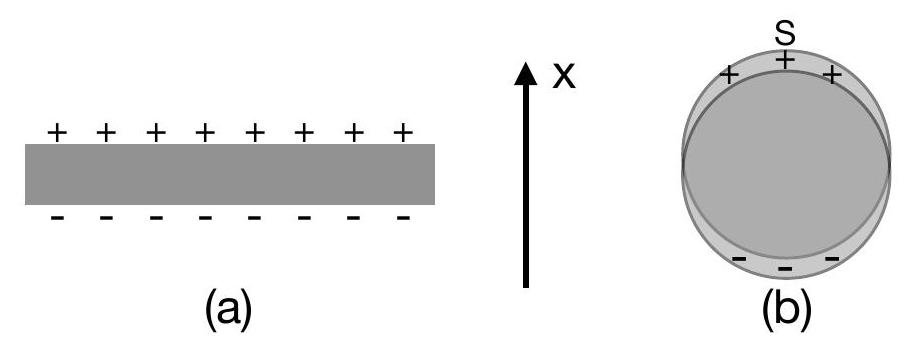
Figure 1 - Illustration des oscillations de charge à la surface d'une plaque mince (a) et d'une sphère ou d'un cylindre (b).
- La densité surfacique de charges est créée par une translation globale des électrons par rapport aux ions, dans une direction perpendiculaire à la plaque. Exprimer
en fonction de l'amplitude de cette translation, de et de . - On admet que le résultat obtenu à la question 1 reste valable lorsque la densité de charges dépend du temps. Écrire l'équation du mouvement d'un électron de la plaque, de masse
, sous l'effet du champ électrique. En déduire que l'amplitude du déplacement des électrons oscille à une pulsation dont on donnera l'expression en fonction de , et de la permittivité du vide .
Nous allons maintenant étudier les oscillations des électrons dans une sphère métallique, représentées sur la figure 1 (b).
4. Dans un premier temps, considérons une sphère uniformément chargée en volume, avec une densité volumique de charge notée
5. On suppose que l'ensemble des électrons du métal a un petit déplacement de translation d'amplitude
champ électrique obtenu par superposition des champs créés par les ions et les électrons, et montrer qu'il est uniforme.
6. Comme pour la plaque, on admet que le résultat obtenu reste valable lorsque
4. Dans un premier temps, considérons une sphère uniformément chargée en volume, avec une densité volumique de charge notée
5. On suppose que l'ensemble des électrons du métal a un petit déplacement de translation d'amplitude
champ électrique obtenu par superposition des champs créés par les ions et les électrons, et montrer qu'il est uniforme.
6. Comme pour la plaque, on admet que le résultat obtenu reste valable lorsque
Nous allons maintenant caractériser brièvement le champ électrique à l'extérieur de la sphère métallique représentée sur la figure 1 (b). Le schéma correspond à un déplacement des électrons parallèle à l'axe
7. Exprimer en fonction du déplacement la densité surfacique de charges au point repéré par la lettre
8. Quel type de champ connu retrouve-t-on à grande distance de la sphère?
9. Tracer, sans calcul, l'allure des lignes de champ à l'extérieur et à l'intérieur de la sphère.
10. Nous avons fait tous les calculs dans l'approximation électrostatique. À quelle condition, portant sur la taille de la sphère, est-il légitime de négliger les phénomènes de propagation?
11. Les valeurs de
12. En utilisant la même méthode que pour la sphère, déterminer la pulsation
13. On considère enfin le cas d'un cylindre métallique de rayon
14. Des expériences réalisées sur des nanoparticules d'or montrent que leurs fréquences d'oscillation dépendent faiblement de leur taille, mais fortement de leur forme. Pour des nanotiges d'or, la pulsation des oscillations longitudinales étudiées à la question précédente est celle d'une onde électromagnétique dans le vide de longueur d'onde 800 nm si
15. Les nanoparticules métalliques peuvent notamment être utilisées pour le traitement des cancers. Elles sont suffisamment petites pour pénétrer dans les cellules de l'organisme, et il se trouve qu'elles sont davantage stockées dans les cellules cancéreuses que dans les cellules saines. Le principe est alors d'envoyer une onde laser dont la pulsation coïncide avec une des pulsations caractéristiques de l'oscillation des électrons dans la nanoparticule. Cette résonance excite le plasmon dont l'amortissement, par des phénomènes qui sortent du cadre de notre étude, produit un dégagement de chaleur qui tue la cellule cancéreuse. Pour que l'onde laser puisse pénétrer dans les tissus biologiques, il faut que sa longueur d'onde soit dans l'infrarouge proche. À la lueur des résultats obtenus plus haut, expliquer pourquoi on utilise des nanotiges d'or, en forme de cylindre allongé, plutôt que des nanosphères d'or.
16. Le chauffage est-il plus efficace si la direction de propagation du laser est parallèle ou perpendiculaire à l'axe du cylindre?
7. Exprimer en fonction du déplacement la densité surfacique de charges au point repéré par la lettre
8. Quel type de champ connu retrouve-t-on à grande distance de la sphère?
9. Tracer, sans calcul, l'allure des lignes de champ à l'extérieur et à l'intérieur de la sphère.
10. Nous avons fait tous les calculs dans l'approximation électrostatique. À quelle condition, portant sur la taille de la sphère, est-il légitime de négliger les phénomènes de propagation?
11. Les valeurs de
12. En utilisant la même méthode que pour la sphère, déterminer la pulsation
13. On considère enfin le cas d'un cylindre métallique de rayon
14. Des expériences réalisées sur des nanoparticules d'or montrent que leurs fréquences d'oscillation dépendent faiblement de leur taille, mais fortement de leur forme. Pour des nanotiges d'or, la pulsation des oscillations longitudinales étudiées à la question précédente est celle d'une onde électromagnétique dans le vide de longueur d'onde 800 nm si
15. Les nanoparticules métalliques peuvent notamment être utilisées pour le traitement des cancers. Elles sont suffisamment petites pour pénétrer dans les cellules de l'organisme, et il se trouve qu'elles sont davantage stockées dans les cellules cancéreuses que dans les cellules saines. Le principe est alors d'envoyer une onde laser dont la pulsation coïncide avec une des pulsations caractéristiques de l'oscillation des électrons dans la nanoparticule. Cette résonance excite le plasmon dont l'amortissement, par des phénomènes qui sortent du cadre de notre étude, produit un dégagement de chaleur qui tue la cellule cancéreuse. Pour que l'onde laser puisse pénétrer dans les tissus biologiques, il faut que sa longueur d'onde soit dans l'infrarouge proche. À la lueur des résultats obtenus plus haut, expliquer pourquoi on utilise des nanotiges d'or, en forme de cylindre allongé, plutôt que des nanosphères d'or.
16. Le chauffage est-il plus efficace si la direction de propagation du laser est parallèle ou perpendiculaire à l'axe du cylindre?
II - Plasmons de surface
Nous allons maintenant nous intéresser aux oscillations électroniques observées au voisinage de la surface plane d'un métal de grande dimension.
17. Écrire l'équation du mouvement des électrons du métal dans un champ électrique uniforme oscillant à la pulsation
18. Établir la relation de dispersion reliant
17. Écrire l'équation du mouvement des électrons du métal dans un champ électrique uniforme oscillant à la pulsation
18. Établir la relation de dispersion reliant
Nous allons maintenant étudier la propagation d'une onde électromagnétique près de la surface d'un métal. On choisit un système de coordonnées cartésiennes tel que cette surface soit le plan
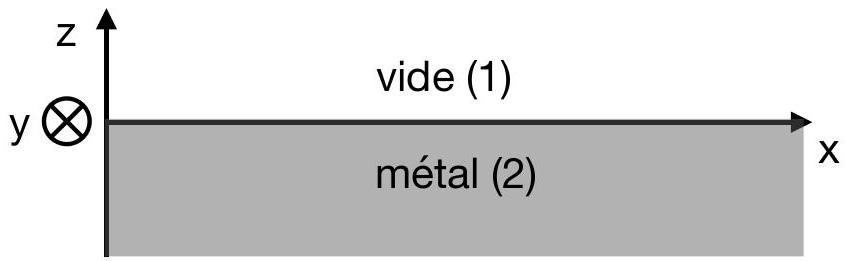
Figure 2 - Schéma de l'interface vide-métal.
- On choisit une onde telle que le champ magnétique
soit dirigé suivant en tout point. Que peut-on alors dire des directions du vecteur d'onde et du champ électrique , dans le vide et dans le métal? - On note
et les amplitudes complexes de suivant et , et on suppose non nul. Exprimer en fonction de et , dans le vide et dans le métal. - On note
l'amplitude complexe du champ magnétique en projection sur l'axe . Exprimer en fonction de et , dans le vide et dans le métal. - En utilisant la relation de dispersion entre
et , éliminer dans l'expression obtenue, et exprimer en fonction de , et . On distinguera les cas du vide et du métal, et on fera intervenir et . - On admet que les composantes de
parallèles à la surface du métal sont continues de part et d'autre de l'interface , et on cherche des solutions telles que ces composantes ne soient pas identiquement nulles. Expliquer brièvement pourquoi ceci implique que et soient identiques dans le vide et dans le métal. - Justifier qu'il apparaît en tout point de la surface du métal une densité surfacique de charges
, reliée à la densité de courant en ce point par , où représente la composante suivant de la densité de courant au même point. - En utilisant l'expression de la conductivité complexe obtenue à la question 17, en déduire la relation entre l'amplitude complexe de la densité surfacique de charge
et l'amplitude complexe de la composante suivant du champ électrique dans le métal. - En utilisant les lois de l'électrostatique, dont on supposera qu'elles restent valables bien que le champ dépende du temps, exprimer
en fonction de et . En utilisant l'expression de obtenue à la question précédente, en déduire le rapport en fonction de et . - En utilisant le résultat de la question 20, en déduire le rapport
en fonction de et . - En utilisant le résultat de la question 22, montrer qu'on obtient la même expression du rapport
si on suppose que est continu en . - On pose
. Les relations de dispersion dans le vide et dans le métal, ajoutées au résultat de la question 27 ou 28 , donnent trois relations entre et , dans lesquelles on éliminera au profit de pour les simplifier. Éliminer et entre ces équations et vérifier la relation
En déduire la relation entre
30. Il existe une première catégorie de solutions avec
31. Le plasmon de surface est une solution dont le champ électrique se propage dans la direction
32. Montrer qu'une telle solution ne peut exister que si
33. En utilisant le résultat de la question 29 et la relation de dispersion dans le vide, éliminer
34. Tracer l'allure de
35. En utilisant les résultats de la question 29, discuter comment les longueurs caractéristiques de décroissance suivant l'axe
36. En prenant la partie réelle de l'amplitude complexe, écrire les composantes suivant
37. Montrer que l'inclinaison des lignes de champ est indépendante de
30. Il existe une première catégorie de solutions avec
31. Le plasmon de surface est une solution dont le champ électrique se propage dans la direction
32. Montrer qu'une telle solution ne peut exister que si
33. En utilisant le résultat de la question 29 et la relation de dispersion dans le vide, éliminer
34. Tracer l'allure de
35. En utilisant les résultats de la question 29, discuter comment les longueurs caractéristiques de décroissance suivant l'axe
36. En prenant la partie réelle de l'amplitude complexe, écrire les composantes suivant
37. Montrer que l'inclinaison des lignes de champ est indépendante de
